ARTIGO

Análise do padrão sazonal e da variação dos preços do milho aos produtores do estado de São Paulo, Brasil

Analysis of seasonal pattern and variation in prices paid for corn producers in São Paulo state, Brazil

Celso Correia de Souza^1*, Daniel Massen Frainer^1,2, José Francisco dos Reis Neto¹, Leonardo Marinho de Carvalho³, Herlones Wuilles dos Santos³ e Luiz Henrique Brito Lemes⁴

¹Professor da Universidade Anhanguera Uniderp, Campo Grande, MS. Brasil;

²Professor da Universidade Estadual de Mato Grosso do Sul – UEMS, Campo Grande, MS. Brasil;

³Mestrando em Produção e Gestão Agroindustrial da Universidade Anhanguera Uniderp, Campo Grande, MS. Brasil;

⁴Graduando em Agronomia – Universidade Anhanguera Uniderp, Campo Grande, MS. Brasil.

(*E-mail: celso.correia@uniderp.edu.br)

---

RESUMO

Este artigo teve como objetivo a análise da variação do nível de preços aos produtores de milho no estado de São Paulo, Brasil. Para tanto, utilizou-se de dados sobre preços desse grão referentes ao período de 2004 a 2015 neste Estado. Considerou-se que o preço é a variável mais importante no planejamento da tomada de decisão do produtor agrícola. Com os resultados obtidos através da análise da média móvel e regressão não linear foi possível averiguar a oscilação do nível de preços do milho durante o período analisado devido a perdas de safras, crises econômicas, etc. Observou-se também através do índice de variação estacional de preços que os meses que proporcionam maiores ganhos econômicos ao produtor corresponde aos meses de outubro a março de cada ano. Da parte do comprador, o melhor período para a compra do milho é de abril a setembro de cada ano.

Palavras-chave: Média móvel; variação estacional de preços; mercado do milho.

---

ABSTRACT

This article intends to make the analysis of change in the price level paid for corn producers in São Paulo state. To this end, we used data on grain prices for the period from 2004 to 2015 in this State. It is considered that the price is the most important variable in the farmer’s decision-making. With the results obtained by the moving average and regression analysis it was possible to ascertain the fluctuation of corn prices level during the period under review due to crop losses, economic crises, etc. Looking through the price seasonal variation index we see that the months that provide greater economic benefits to the producer corresponds to the months of October to March each year. On the part of the buyer, the best period for the purchase of corn is from April to September.

Keywords: Moving average; price seasonal variation; corn market.

---

Introdução

Na região Leste do Brasil o milho é cultivado em duas ocasiões por ano, a primeira safra, ou safra de verão, ocorre no período de agosto a fevereiro e a segunda safra, denominada de safrinha, ocorre no período de janeiro a julho de cada ano.  No estado de São Paulo (SP), a cultura de milho ocupa, na safra de verão a sexta e na safra de inverno a quinta posições no ranking nacional, com volume na ordem de quatro milhões de toneladas, ficando atrás dos estados de Mato Grosso, Paraná, Mato Grosso do Sul e Goiás (CONAB, 2015).

O Brasil se destaca entre os principais países produtores de milho, ocupando a terceira posição, atrás da China e dos Estados Unidos. Atualmente, o Brasil exporta em torno de 18% da produção nacional. Esse processo de participação no mercado externo se deu ao longo do tempo, principalmente, a partir de 2001 (Richetti e Ceccon, 2009; Duarte et al., 2011; Richetti, 2012).

De acordo com Duvick (1992), o potencial produtivo do milho no país é o resultado da soma da melhoria genética (47,75%), isto é, a utilização de técnicas de manejo que sejam adequadas a cada ambiente de cultivo, e das condições ambientais (52,25%). Assim, foi possível aumentar a produtividade média do milho no Brasil, obtendo-se 5,2 t/ha. No estado de SP a produtividade média gira em torno de 5,3 t/ha.

Nos estados do Paraná e Mato Grosso do Sul os maiores rendimentos de milho safrinha são obtidos com o plantio entre a primeira quinzena de fevereiro e a primeira quinzena de março. Já, nos estados de Mato Grosso e Goiás, os maiores rendimentos são obtidos com o plantio no mês de fevereiro. No estado de SP, o período de plantio se estende até o mês de abril (Duarte et al., 2011; Abimilho, 2016).

Segundo Hoffmann (1998), o domínio da variação estacional dos preços da agricultura é de extrema importância para direcionar as decisões dos produtores agrícolas e dos comerciantes, bem como, para articulação de políticas agrícolas do governo. Desta forma, a análise da formação de preços no mercado agrícola é extremamente importante para orientar produtores na tomada de decisão de quanto produzir e para quem vender com o objetivo de maximizar seus lucros.

De uma forma geral, os preços dos produtos agropecuários são instáveis ao longo do tempo por influência dos seguintes fatores: clima, pragas, dificuldades de previsão e sazonalidade da produção de alimentos. Esses fatores dificultam o ajuste entre a produção e as nuances do mercado, o que obriga o produtor a ter maior cuidado com as oscilações de preços. Vários autores apontam para um comportamento volátil, tanto na produção quanto do preço do milho, provocando inconstância ao produtor (Bottini et al., 1995; Camargo Filho e Mazzei, 2001; Cruz e Pereira Filho, 2002).

A produção agropecuária apresenta uma adequação bastante complexa às necessidades do mercado. Isso ocorre porque o consumo se mantém praticamente contínuo ao longo do ano ou cresce a taxas baixas entre os anos, sendo impulsionado pelo crescimento da população e pela elevação da renda per capita, enquanto que a produção é instável e descompassada no tempo (Mendes e Padilha Júnior, 2007; Santos et al., 2007).

Diante do exposto, este estudo tem como objetivo a compreensão da variável preço no contexto do planejamento e da tomada de decisão de comercialização do milho, no mercado atacadista do estado de SP, através da análise de uma série histórica de preços, no período de 2004 a 2015. Essa análise de certa forma reflete a variação de preços ao nível nacional. Para a consecução desse objetivo fez-se necessário determinar o índice estacional de preços e os limites de confiança dos preços do milho ao longo do ano, tanto do ponto de vista do produtor quanto do comerciante; eliminar os efeitos das sazonalidades dos preços do milho através da determinação das médias móveis centradas dos preços desse produto.

Esta pesquisa foi desenvolvida em quatro tópicos, no primeiro a introdução da pesquisa contendo a contextualização, a justificativa, a conjuntura problemática, os objetivos propostos e a organização do estudo. No segundo tópico foram apresentados os aspectos metodológicos como o método de coletas de dados secundários, a tipologia da pesquisa, e tipos de análises de dados usados. Também, foram apresentados tópicos sobre séries temporais, índice de variação estacional, limites de confianças inferior e superior, aproximação polinomial e análise de variância, recursos matemáticos necessários à consecução da pesquisa. No terceiro tópico, de resultados e discussão foram apresentados os resultados da pesquisa, acompanhados de quadros e gráficos devidamente discutidos. Já, no último tópico foi apresentada a conclusão do estudo realizado neste trabalho acadêmico.

Material e Métodos

Essa pesquisa pode ser classificada como bibliográfica, pois, inicialmente, foi feito um levantamento bibliográfico dos assuntos que envolviam o tema em estudo; em seguida, uma revisão bibliográfica desses assuntos para a fixação dos conceitos que foram utilizados. Também, deve ser classificada como exploratória descritiva, pois, procurou-se, através de dados de preços do milho, pagos ao produtor, descobrir e observar fenômenos, procurando descrevê-los, classificá-los e interpretá-los, ao mesmo tempo em que se procurou explorar, no problema de pesquisa, a tendência do comportamento dos preços do milho (saco de 60 kg).

Para a realização deste trabalho utilizou-se dados secundários dos preços pagos aos produtores na comercialização de milho, saco de 60 kg, no estado de SP, no período de janeiro de 2004 a dezembro de 2015, disponíveis no Instituto de Economia Agrícola (IEA). Os dados mensais do histórico de preços do milho entre 2004 e 2015 foram resumidos em planilhas para facilitar a manipulação.

Devido à constante desvalorização do real (R$), moeda nacional brasileira, motivada pela inflação, tornou-se necessário corrigir os preços do saco de milho em relação ao período de tempo estudado, com a determinação dos preços reais na moeda corrente usando-se a série histórica, nesse mesmo período de tempo, do Índice de Preço ao Consumidor Amplo (IPCA), referida essa correção a dezembro de 2015.

Na análise do comportamento do valor do milho no período foi usado o modelo clássico de série temporal centrada, dividida em quatro padrões: Tendência (T), que é o comportamento de longo prazo da série, que pode ser causada pelo crescimento demográfico, ou mudança gradual de hábitos de consumo, ou qualquer outro aspecto que afete a variável de interesse no longo prazo; Variações cíclicas ou ciclos (C), flutuações nos valores da variável com duração superior a um ano, e que se repetem com certa periodicidade. Podem ser variações climáticas ou na economia; Variações sazonais ou sazonalidade (S), flutuações nos valores da variável com duração inferior a um ano. Podem estar ligadas às estações do ano, períodos de cobranças de impostos, etc. Se os dados forem registrados anualmente, não haverá sazonalidade; Variações irregulares (I), que são as flutuações inexplicáveis, como catástrofes naturais, atentados terroristas, etc. (Spiegel, 2001; Hoffmann, 1998).

A decomposição de uma série temporal em padrões é muito útil, pois, permite identificar quais componentes estão atuando naquele conjunto em particular. Existem dois modos de decomposição de uma série temporal: o modo aditivo e o multiplicativo. No modelo aditivo o valor da série é Y = T + C + S + I ou Y = T + C + I se os dados forem registrados anualmente. Em não havendo variações irregulares, o modelo se resume em Y = T + C. No modelo multiplicativo o valor da série Y = T×C×S×I ou Y = T×C×S se os dados forem registrados anualmente, em que não existe a sazonalidade e Y = T×C, na ausência de variações irregulares (Hoffmann, 1998).

Chamando de Y a variável dependente e T, C, S e I de variáveis independentes, o modelo geral de série temporal é apresentado pela equação 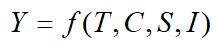(1).

                                              (1)

Observe que no modelo aditivo as variáveis independentes têm a mesma unidade da variável dependente e no modelo multiplicativo, o produto das unidades das variáveis independentes produz a mesma unidade da variável dependente.

Como a tendência indica o comportamento da série de longo prazo, isto é, se ela cresce, decresce ou permanece estável, e qual a velocidade dessas mudanças, se houver, nos casos mais simples trabalha-se com tendência constante, linear ou quadrática. Os valores das outras componentes modificam a tendência e seus valores são em torno de 1 (se maiores do que 1 aumentam a tendência, se menores diminuem a tendência, se exatamente iguais a 1 não causam efeito). O modelo a ser adotado depende da série de dados e das características intrínsecas do problema. Se as variações forem regulares utiliza-se o modelo aditivo, caso contrário, o multiplicativo (Spiegel, 2001; Hoffmann, 1998).

A determinação da tendência auxilia na avaliação do comportamento de uma série temporal e de sua utilização em previsões. A tendência pode ser removida da série temporal para facilitar a visualização das outras componentes e, identificar a faixa típica de valores que a variável pode assumir quando não existe um comportamento crescente ou decrescente ao longo do tempo.

As equações (2) e (3) tratam da remoção da tendência nos modelos aditivo e multiplicativo, respectivamente.

                                         Modelo aditivo: 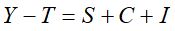                                       (2)

                                      Modelo multiplicativo: 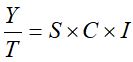                                    (3)

No modelo aditivo, com a remoção da tendência, os valores da série oscilam em torno de zero. Se forem iguais a zero, a tendência não é afetada pelos fatores sazonais, cíclicos e irregulares, se maiores do que zero indicam aumento da tendência e, se menores que zero, diminuem a tendência.

Já, no modelo multiplicativo, com remoção da tendência, os valores oscilam em torno de 1. Se forem iguais a 1, os fatores sazonais, cíclicos e irregulares não afetam a tendência, se forem diferentes de 1, mas com erro para 1 de até 5%, a tendência também não será afetada pelos fatores sazonais, cíclicos ou irregulares e, se o erro em torno de 1 for maior do 5%, a tendência será afetada por esses fatores.

A obtenção da tendência pode ser feita através de modelos de regressão ou de médias móveis. Segundo Morettin e Bussab (2014), regressão é uma técnica de análise matemática que utiliza a relação entre duas ou mais variáveis quantitativas para determinar um modelo matemático de forma que o efeito sobre uma variável pode ser previsto através da outra variável (ou outras variáveis).

Na análise de experimentos, o modelo matemático mais empregado para tentar explicar o efeito dos tratamentos na variável reposta é o modelo polinomial. O polinômio ajustado (equação de regressão) é da forma da equação 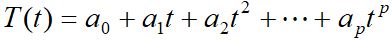(4).

                                 (4)

Onde 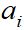, i = 1, 2, ..., p, são os parâmetros a serem determinados e p é o grau do polinômio do modelo. No caso dos experimentos, a variável t, ou variável independente, é uma variável não aleatória que corresponde aos tratamentos e a variável T, ou variável dependente, que é a variável resposta (variável aleatória).

O método de regressão, com a utilização de análise de variância consiste em determinar se os polinômios obtidos explicam satisfatoriamente a relação entre os tratamentos utilizados e as observações. Para tanto, emprega-se o teste F para determinar quais são os modelos possíveis e o coeficiente de determinação (R²) para mostrar o grau de explicação de cada modelo.

O teste F na análise de variância permite testar apenas o coeficiente associado à variável t no expoente p, que melhor se ajusta ao problema estudado, testando-se assim o efeito de grau p. O coeficiente de determinação R² é dado pela equação (5).

                                        (5)

Onde SQregressão = soma dos quadrados dos efeitos da regressão e SQtratmentos = soma dos quadrados dos tratamentos. Quanto mais próximo de 100% o valor de R², melhor se ajustam os dados do problema estudado ao modelo de regressão encontrado (Morettin e Bussab, 2014).

A determinação da tendência (T) por médias móveis é feita, segundo Zilli e Barcelos (2006), calculando-se a média aritmética dos primeiros k períodos da série, colocando o resultado no período t, exatamente no centro dos k períodos. Se 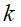 for ímpar, isto é,  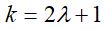termos, onde  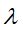é um número inteiro positivo menor do que t, a média móvel 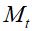, correspondente a  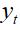é dada pela equação 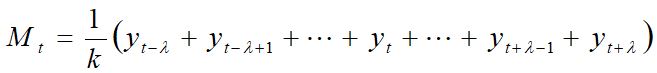(6).

           (6)

Onde 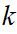= número de períodos,  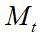média móvel no instante (período)  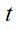e, 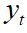 = valor do termo da série no período .

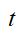Quando 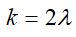, isto é, k é um número par, um valor qualquer da média móvel não corresponde exatamente a nenhum termo y_t da série em estudo. Para sanar essa dificuldade, médias móveis de dois períodos, calculadas a partir daquelas de k períodos, precisam ser obtidas para obter resultados centrados.

Para k par ou ímpar, as próximas médias da série são calculadas progressivamente, acrescentando-se um período seguinte e desprezando-se o primeiro período utilizado para o cálculo da média móvel anterior. E assim, as novas médias vão se movendo até o fim da série. Observe que a série final das médias móveis de k períodos, se perdem os k/2 períodos iniciais e os k/2 períodos finais relativos à série original. O número total de períodos (n) da série é chamado de ordem da série.

Quanto maior o número de períodos da série, agrupados pelas médias móveis, mais "alisada" fica a linha de tendência e, quanto menor o número de períodos, mais a tendência acompanhará os dados originais. Por este motivo, quando uma série apresenta muitas irregularidades é comum "alisá-la" através de médias móveis.

As variações sazonais de uma série temporal são oscilações de curto prazo, que ocorrem sempre dentro do ano, e que se repetem sistematicamente ano após ano. Existem vários métodos para a obtenção das variações sazonais, bem como os limites inferior e superior de variação no período, denominados de limites de confiança inferior e superior, respectivamente. Segundo Arias et al. (2009), dentre os métodos mais utilizados, destaca-se o índice de variação estacional (IVE), definido pela equação 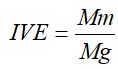(7).

                                                        (7)

Onde 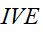= Índice de variação estacional; 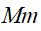= média aritmética mensal em cada período e; 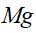= média geral dos valores da série no período. Ainda, segundo Arias et al. (2009), os cálculos para os limites de confiança inferior e superior no período são obtidos através das equações (8) e (9), respectivamente.

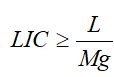                                                         (8)

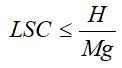                                                        (9)

Onde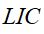= limite inferior de confiança, 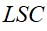= limite superior de confiança, 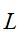= menor valor mensal da série em cada ano e, 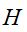= maior valor mensal da série em cada ano.

Com a série dos preços do milho devidamente corrigida, são calculados os índices: Índice de Variação Estacional (IVE), Limite Inferior de Confiança (LIC) e o Limite Superior de Confiança (LSC), que podem ser analisados tanto do ponto de vista do produtor vendedor quanto do ponto de vista do comprador.

Ainda, com relação à série histórica dos preços do saco de milho corrigidos pelo IPCA, determina-se a série das médias móveis, em que se considerou um período de 12 meses (um ano) para a eliminação de variações sazonais da série, já estudadas quando do cálculo do IVE. Com isso, o gráfico de tendência fica muito mais “alisado”.

Como não existiu, durante a série histórica dos dados pesquisados, nenhum fenômeno irregular que pudesse alterar a produção do milho, o parâmetro ligado à variação irregular I foi eliminado do modelo (I = 0). Desse modo, foram eliminados a variação sazonal S, pela escolha de um período de 12 meses no cálculo da média móvel e a variação irregular I, restando somente a tendência T e a variação cíclica C os modelos aditivo e multiplicativo da série temporal, equação (10).

                                                       (10)

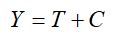
Para que se pudesse fazer previsões sobre os preços do saco de milho em determinados instantes tanto no período interior quanto no exterior ao tempo considerado da série (2004 a 2015), foi determinada a equação de ajustamento polinomial da série dos valores das médias móveis, equação (4), bem como, o respectivo coeficiente de ajustamento R², equação (5), para o estabelecimento da explicação do modelo.

Resultados e Discussão

O Quadro 1 apresenta a série histórica, de 2004 a 2015, dos preços do saco de 60 kg de milho pagos ao produtor rural do estado de SP (IEA, 2015).

O Quadro 2 apresenta a mesma série histórica do Quadro 1, agora corrigida mensalmente pela inflação do período de 2004 a 2015, segundo o Índice de Preços ao Consumidor Amplo (IPCA), do Instituto Brasileiro de Geografia e Estatística (IBGE), referido a dezembro de 2015 (IBGE, 2016).

Cálculos dos Índices de Variação Estacional e dos Limites de Confiança

Utilizando as equações (7), (8) e (9), foram calculados o índice de variação estacional (IVE), o limite inferior de confiança (LIC) e o limite superior de confiança (LSC), respectivamente, mostrados no Quadro 3.

Do Quadro 3 fica evidente que os meses com os maiores IVE, acima de 100%, foram de outubro a março, em que o preço médio do milho ficou acima do esperado. A partir de janeiro a tendência foi de queda do preço do milho, ficando abaixo de 100% a partir do mês de abril, continuando com esse comportamento até setembro, mas já com tendência de alta a partir desse mês, ficando acima de 100% até o mês de março.

Não se levando em conta os riscos inferiores e superiores, quando o IVE estiver acima de 100% a comercialização do milho é favorável ao produtor e desfavorável ao comprador, ocorrendo o contrário quando o IVE está abaixo do nível de 100%. A Figura 1 retrata o comportamento do IVE do preço do saco de 60 kg de milho no estado de SP, bem como e os limites inferior e superior de confiança, LIC e LSC, respectivamente.

Da Figura 1, conclui-se que de outubro a março o produtor tem chances de vender o seu produto a um preço alto (IVE acima de 100%), mas correndo o risco de vendê-lo a um preço muito baixo entre janeiro e abril (curva LIC distante da curva IVE). Observe que nos meses de novembro, dezembro, janeiro e julho são os meses em que o produtor tem maiores chances (riscos) de maiores ganhos econômicos, meses em que a curva LSC está mais distante de IVE. Coincidentemente, existe algum risco de prejuízo na comercialização do milho pelo produtor nos meses de dezembro e janeiro, pois, as distâncias do IVE para o LIC são grandes, representando riscos de vendas do milho a preços bem inferiores aos praticados historicamente, o que pode causar prejuízos ao produtor.

Do ponto de vista do comprador, o melhor período para a compra do milho é de abril a setembro, quando a curva do IVE está abaixo do nível de 100%. Destacam-se ainda os meses de fevereiro, março, abril, agosto, setembro e outubro como ótimos meses para o comprador efetuar a sua compra de milho, pois, apesar de que, em alguns desses meses, estar pagando um valor pelo saco do milho um pouco acima do nível de 100%, o risco de pagar um preço muito alto é pequeno, pois, o milho, historicamente, não atinge um preço muito alto nesses meses (curva LSC próxima da curva IVE).

Por outro lado, o comprador pode ser favorecido nos meses de janeiro, fevereiro março e abril, em que preços do saco de 60 kg do milho podem estar bem abaixo da média histórica, comprando o milho a um preço bem vantajoso, comportamento esse explicado pelo distanciamento entre as curvas IVE e LIC nessas datas.

Equação da tendência

No presente estudo foi adotado o modelo aditivo das séries temporais sem as componentes sazonalidade (S=0) e irregular (I=0), pois, nenhum dos fenômenos sobre sazonalidade   e aleatório e inexplicável foram detectados no período que pudesse provocar uma variação no preço do milho, a da série temporal ficou em função das componentes de tendência T e cíclica C, equação (10).

                                                               Y = T + C

Inicialmente, do Quadro 2, calculou-se as médias móveis de 12 períodos da série histórica dos preços do saco de 60 kg de milho, pagos aos produtores do estado de SP, obtendo-se o Quadro 4.

Para analisar o comportamento das médias móveis (Quadro 4), determinou-se a equação de tendência através de aproximações polinomiais, equação (4), encontrando um polinômio T(t) de grau 6, como aquele que melhor se ajustou à série das médias móveis dos preços do saco de 60 kg do milho pagos aos produtores.

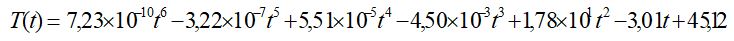    (11)

O sucesso na previsão dessa equação está acima de 50%, equação (5). Na Figura 2 estão representados os gráficos das séries históricas dos preços do saco de 60 kg de milho pagos aos produtores, em valores nominais, em valores corrigidos pelo IPCA, da série das médias móveis e da curva ajustada da tendência das médias móveis.  Observe que o gráfico da equação polinomial ficou mais alisado do que o gráfico das médias móveis.

Da Figura 2 observa-se que, a partir do ano de 2004, houve uma redução no nível de preços do milho estendendo-se até maio de 2006. Essa tendência da redução dos preços nesse período se deu pelo fato que no ano de 2004 obteve-se um recorde na produção, na ordem de 42 milhões de toneladas, acompanhada pela redução na demanda externa, isto é, a exportação do Brasil caiu de 5 milhões de toneladas para 1 milhão de toneladas nesse período (MAPA, 2010).

 A partir de maio de 2006 começa uma tendência de elevação do nível de preço do milho, puxado pelo crescimento na demanda externa, principalmente, pelo Estados Unidos para a produção de etanol, o que contribuiu para que as exportações no Brasil alcançassem o patamar de 11 milhões de toneladas. Tal fato explica o pico de elevação do nível de preços no estado de SP, entre 2007 e 2008, demonstrado pela série das médias móveis dos preços.

No estado de SP as exportações atingiram 119.500 toneladas em 2008, reduzindo para 27.900 toneladas em 2009 em razão da redução da demanda externa. A recuperação dos preços a partir de 2010 ocorreu em virtude do aumento no consumo animal, ou seja, na suinocultura o consumo de milho cresceu em torno de 3%, bem como, na pecuária leiteira. Nos demais segmentos de animais o crescimento do consumo deste grão ficou em torno de 4% (IEA, 2010).

Como o período de dados da série temporal varia de 01/01/2004 à 31/12/2015, um total de 144 meses, uma previsão para o preço do saco de 60 kg de milho em janeiro de 2016, basta fazer t = 145 na equação (11), obtendo-se o valor de R$31,96. O valor real do preço do saco de 60 kg de milho em janeiro de 2016 foi de R$36,39, bem acima do valor obtido pela equação de tendência. Realmente, no mês de janeiro de 2016 aconteceu uma valorização extraordinária do milho devido a perdas de safra em várias partes do mundo.

Variações cíclicas

A série das médias móveis (Quadro 4) foi construída de modo que desaparecesse a sazonalidade (S = 0), como também não existiu nenhuma variação irregular (I = 0), restou testar se existem variações cíclicas (C) que tinham influencias no preço do saco de milho. Calculou-se então os valores de C, do modelo aditivo, equação (10).

                                                             Y – T = C

A Figura 3 apresenta o gráfico do parâmetro cíclico C, que é a diferença da série histórica corrigida (Quadro 2) para os correspondentes valores da tendência T das médias móveis, equação (4), do ajuste polinomial.

Pode-se observar, na Figura 3, que não há alternância sistemática entre valores maiores e menores do que zero, isto é, os preços não oscilam de um mês para outro, ou seja, não se consegue identificar a existência de ciclos. Comportamentos semelhantes são observados para os demais anos da série temporal. Então pode-se desprezar o efeito das variações cíclicas na série temporal (C = 0).

Conclusões

A busca de um padrão de preços do milho (saco de 60 kg) comercializado no estado de SP indicou que não existe uma sazonalidade bem caracterizada nessa comercialização, pois, os melhores preços recebidos pelos produtores aconteceram no período de outubro a março de cada ano, no pico da safra de verão, influenciados pelos baixos estoques da indústria nesse período, e os piores preços recebidos aconteceram entre abril e setembro, durante a safrinha, em que a indústria está estocada do produto.

Do ponto de vista do produtor na comercialização de milho, de outubro a março ele tem chances de vender o seu produto a um preço alto (IVE acima de 100%), mas correndo o risco de vendê-lo a um preço muito baixo entre janeiro e abril. Durante o período de abril a setembro, apesar de o produtor receber menor remuneração pelo seu produto, ele não corre tanto risco de vender a um preço muito baixo, com chances até de vendê-lo a um preço mais alto, com base nos limites de confiança LIC e LSC.

Observou-se, também, que o comportamento da série histórica do preço do milho não possui as componentes sazonal, cíclica e irregular, sendo somente caracterizada pela tendência. Na análise dessa série histórica aconteceram diversas variações bruscas cujas causas foram perdas de safras, crises econômicas, etc.

Referências Bibliográficas

ABIMILHO (2016) - Oferta e Demanda do Milho do Brasil. Associação Brasileira das Indústrias do Milho. < http://www.abimilho.com.br/estatisticas>. [cit. 2016.01.18].         [ Links ]

Arias, E.R.A.; Souza, C.C.; Flores, J.M. e Pereira, M. de M. (2009) - Estacionalidade dos preços e da quantidade comercializada de milho verde no mercado atacadista do Ceasa de campo grande, estado do Mato Grosso do Sul. Informações Econômicas, vol. 29, n. 3, p. 29-37.         [ Links ]

Bottini, P.R.; Tsuneshiro, A. e Costa, F.A.G. da (1995) - Viabilidade da produção de milho verde na “safrinha”. Informações Econômicas, vol. 25, n. 3, p. 49-55.         [ Links ]

Camargo Filho, W.P. de e Mazzei, A.R. (2001) - Estacionalidade de alcachofra, cogumelo, milho verde e hortaliças condimentares.  Informações Econômicas, vol. 31, n. 1,p. 63-69.         [ Links ]

CONAB. (2015) –Acompanhamento da safra brasileira de grãos, v. 2, Safra 2014/2015- Quarto Levantamento. Brasília: Companhia Nacional de Abastecimento., p. 57-64.         [ Links ]

Cruz, J.C. e Pereira Filho, I.A. (2002) - Manejo e tratos culturais para o cultivo do milho verde. Embrapa Milho e Sorgo, Sete lagoas, MG. 9p.  (Embrapa Milho e Sorgo.  Circular Técnica, 16).         [ Links ]

Duarte, J. de O.; Garcia, J.C. & Miranda, R.A. de (2011) - Cultivo do milho: mercado e comercialização. Embrapa Milho e Sorgo, 2011.         [ Links ]

Duvick, D.N. (1992) - Genetic contributions to advances in yield of U.S. maize. Maydica, vol. 37, n. 1, p. 69-79.         [ Links ]

Hoffmann, R. (1998) - Estatística para economistas. Pioneira, São Paulo. 430 p.         [ Links ]

IBGE (2016) – Índice de Preços ao Consumidor Amplo – IPCA.  2016. Instituto Brasileiro de Geografia e Estatística. < http://www.ibge.gov.br/home/estatistica/indicadores/precos/inpc_ipca/defaultinpc.shtm>. [cit. 2016.11.09].         [ Links ]

IEA (2010) –Primeira Estimativa de Oferta e Demanda de Milho no Estado de São Paulo em 2010. Análises e indicadores do agronegócio, vol. 5, n. 3, março/2010. Instituto de Economia Agrícola. <www.iea.sp.gov.br/out/verTexto.php?codTexto=11872>. [cit. 2016.01.         [ Links ]15].

IEA (2015) - Instituto de Economia Agrícola. Banco de Dados. < http://www.iea.sp.gov.br/out/bancodedados.html>. [cit. 2016.01.15].         [ Links ]

Mendes, J.T.G. e Padilha Júnior, J.B. (2007) - Agronegócio: uma abordagem econômica. Pearson Prentice Hall, São Paulo.         [ Links ]

MAPA (2010) – Sumário executivo milho. Ministério da Agricultura Pecuária e Abastecimento. < www.agricultura.gov.br/politica-agricola/publicacoes>. [cit. 2016.01.11].         [ Links ]

Morettin, P.A. e Bussab, W. de O. (2014) - Estatística básica.6. ed. Rev. atual. Saraiva, São Paulo.         [ Links ]

Richetti, A. (2012) - Viabilidade econômica da cultura do milho safrinha, 2013, em Mato Grosso do Sul. Embrapa Agropecuária Oeste, Dourados. 11 p. (Embrapa Agropecuária Oeste. Comunicado técnico, 182).         [ Links ]

Richetti, A. e Ceccon, G. (2009) - Análise econômica de sistemas de produção de milho safrinha em cultivo consorciado. In: Seminário nacional de milho safrinha, 10. Rio Verde. Anais... Rio Verde: ABMS: FESURV. p. 207-213.         [ Links ]

Santos, C.C.; Toledo Filho, J.R.; Knuth, V.; Cardoso, A.F. e Souza, V. (2007) - A gestão contábil nas atividades do agronegócio e agropecuário como ferramenta gerencial para tomada de decisões nos períodos de sazonalidade. In: Londrina, 22 a 25 de julho de 2007, Sociedade Brasileira de Economia, Administração e Sociologia Rural - SOBER. < http://www. sober.org.br/palestra/6/34.pdf>. [cit. 2016.11.07].         [ Links ]

Spiegel, M.R. (2001) - Estatística. Editora Makron, Rio de Janeiro.         [ Links ]

Zilli, J.B. e Barcellos, G.M. (2006) - Padrão de variação estacional dos preços do arroz no estado do Rio Grande do Sul. Informações Econômicas, vol. 36, n. 3.         [ Links ]

 

Recebido/received: 2016.08.16

Recebido em versão revista/received in revised form: 2016.11.17

Aceite/accepted: 2016.11.18