Serviços Personalizados
Journal
Artigo
Indicadores
Links relacionados
Compartilhar
Portugaliae Electrochimica Acta
versão impressa ISSN 0872-1904
Port. Electrochim. Acta vol.29 no.4 Coimbra 2011
Investigation of Passive Film Properties and Pitting Resistance of AISI 316 in Aqueous Ethanoic Acid Containing Chloride Ions using Electrochemical Impedance Spectroscopy(EIS)
Neelima Mahato* and M.M. Singh
Department of Applied Chemistry, Institute of Technology, Banaras Hindu University, Varanasi, 221 005, India
Abstract
The structure and properties of the passive film formed on the surface of AISI 316 stainless steel in aqueous ethanoic acid have been investigated using EIS. Experiments were carried out at 30 °C in different concentrations of ethanoic acid. Effects on the film properties due to the change of electrode potential, exposure durations and addition of chloride ions to the electrolyte were also studied. Impedance parameters were determined using simple model and equivalent electrical circuit. Results suggest the formation of multilayered passive film on the steel surface. The film possessed dual structure. Inner layers were thin and compact, whereas the outer layer was porous and defective. The measured capacitive behavior was of non ideal nature and hence replaced by constant phase element or CPE. Formation of the passive film and the change in its structure has been explained using impedance parameters.
Keywords: Constant phase element, CPE factor, passive film, pseudo inductance, pitting.
Introduction
AISI 316 austenitic stainless steels have been developed for their applicability and extensive use in moderate to severe corrosive conditions. The steel exhibits high corrosion resistance, primarily, due to the formation of a passive film on its surface. Researchers [1-4] have reported that the passive film formed on stainless steel surface responds to ac signals and a lot of information regarding film properties, kinetics and mechanism of corrosion process can be provided by ac impedance measurements. EIS has become a very powerful technique in corrosion science. One of the principle advantages of EIS over traditional dc techniques is that EIS can be well performed in low solution conductivity, which was a problem that may affect the electrochemical measurements of dc techniques. Also EIS is a non destructive technique (small signal applied during the measurements), so that EIS measurements can be repeated several times using the same electrochemical cell without altering its electrochemical properties [5].
Impedance investigations in aqueous mineral acid media have been reported extensively till recent past, but, reports in organic acids are scanty. Ethanoic acid is extensively used in processing, pharmaceutical, refinery and petrochemical industries. Impedance behavior of AISI 316 SS in ethanoic acid exhibits a variety of features owing to its alloy composition and therefore, a systematic study provides valuable information regarding the properties of steel in organic acid media. Since, the interpretation of results is the most important part of impedance investigations and therefore, it is essential to pick the right model to explain the results. The method employed in this communication is convenient to apply in any other steel-organic acid system.
The commonly observed features during the impedance measurements of AISI 316 SS are depressed semicircle, non ideal capacitance and pseudo inductance. Theoretically, in ideal cases, the Nyquist plot is a semicircle with its center on the x-axis. Depressed semicircles are explained by a number of phenomena depending on the nature of the system being investigated. Either some properties of the system are not homogeneous, or there is distribution (dispersion) of the values of the same feature at different locations over the electrode surface. This causes requirement to incorporate a new element in the equivalent electrical circuit, i.e., non ideal capacitance (defined as constant phase element CPE) in place of ideal capacitance. Mathematically, CPE may be defined as [6]:

where, ZCPE is CPE's impedance and A is the CPE parameter. It is admittance (1/|Z|) at ω = 1 rad sand has unit of Ω-1 cm-2 s-1. i is the imaginary number (i = (-1)-1/2) and ω is the angular frequency (ω = 2πf, f being the frequency). A consequence of this simple equation is that the phase angle of the CPE impedance is independent of the frequency and has a value of (- n × π/2) degrees. This gives CPE its name. When n = 1, the equation becomes

This is the same as that for the impedance of an ideal capacitor, where A = C. When n is close to 1.0, the CPE resembles a capacitor, but the phase angle is not 90 °. It is constant and somewhat less than 90 ° at all frequencies. In these cases, the 'true' capacitance can be calculated from A and n. The factor n is defined as

where, α is the depression angle (in degrees) that evaluates the semicircle depression (of Nyquist plot). In many cases, this impedance element is introduced formally only for fitting impedance data. The CPE element may be related to a number of different interfacial phenomena. The most straightforward interpretation is to consider it as a dispersive capacitance of the double layer. [7,8]. It is thought to arise from a distribution of the relaxation times resulting from heterogeneities of microscopic level at oxide/electrolyte interface [6, 9, 10]. According to Cox and Wong, the CPE behavior is attributed to a geometric origin, such as, surface heterogeneity or surface roughness [11]. The factor n or CPE power is therefore, also known as roughness coefficient. The slope of the linear part of Bode plots gives the value of n. Its value generally decreases with the increase in surface roughness.
When n = 1, the CPE describes an ideal capacitor corresponding to the conventional double layer capacitance. It behaves like a resistor for n = 0, and an inductor for n = (-1). A protected smooth and bright surface in electrolytic solution often has n > 0.8. Surface undermined by corrosion can have values ranging from 0.8 for even general corrosion, to 0.6-0.7 for uneven general corrosion. The value n = 0.4 - 0.5 is found for uneven localized corrosion or wide pits and the CPE represents Warburg impedance involving diffusion processes [12]. The value of n is an adjustable parameter that always lies between 0.5 and 1. It is found to vary at different potentials corresponding to different regions on the Tafelâs plot. This fact is associated with the changes in the structure or composition of the passive film on steel surface.
The pseudo inductance is characterized by a position of impedance spectrum appearing in the fourth quadrant when the data set is plotted as real impedance component versus the negative of imaginary component. Such type of frequency responses is observed in electrochemical impedance measurements for a number of corroding systems [13, 14]. This behavior arises from a number of sources [15], such as, adsorption processes. It is called pseudo because the process giving rise to inductance is probably not like those of a real inductor [16]. According to Kendig [17], it is caused by a non linear frequency response resulting from irreversible desorption of the adsorbed intermediates. Armstrong et al. [18] and Epelboin et al. [19] have proposed methods to model pseudo inductive frequency responses and extract corrosion rate information from ac impedance data.
In principle, an electrochemical process may be modeled by equivalent electrical circuit elements, such as, resistors, capacitors and inductors. The interpretation of electrochemical impedance spectra requires selection of an appropriate model. The selection of an appropriate model can be time consuming, particularly, if a detailed study is desired. A number of programming methods for computing circuit parameters are available in the literature [20-23]. In this study, we have used our own algorithm implemented on Mathematica 7.0 (commonly and extensively utilized for analyzing mathematical and numerical problems) for analyzing the results and computing the electrical circuit. We present here the results of ac impedance investigation of AISI 316 in aqueous ethanoic acid under different experimental conditions, such as, concentration of acid, duration of exposure, change of applied electrode potential and effect of chloride ions. The aim of this work was to study the formation and changes in the structure and properties of passive film during corrosion and pitting of AISI 316 in ethanoic acid medium. In the present communication, the discussion is divided into four sections viz., (a) effect of exposure time, (b) effect of concentration, (c) effect of applied potential and (d) effect of chloride ion addition.
Experimental
Materials and methods
All the chemicals were procured from Merck, India Ltd. AISI 316 stainless steel sheets of thickness 1 mm with composition 16.5-18% Cr, 12.5-15.0% Ni and 2.0-3.0% Mo were procured from Good Fellow, England. The sheets were cut and filed into rectangular pieces of dimensions 3 cm x 1 cm. The specimens were polished mechanically up to mirror finish on a polishing wheel attached with emery papers (numbers 100 to 2000) of varying grit size. The mirror polished surfaces were cleaned properly by washing with distilled water followed by rinsing with acetone and drying in air. Each single piece was attached to a copper plate with an extended wire sealed in a glass tube and fixed with screw. An area of 1 cm2 on one side of the specimen was left exposed. This assembly was taken as the working electrode for electrochemical studies. Ag/AgCl (Orion, Beverly, M.A. USA) electrode was used as the reference electrode and a Pt wire as counter electrode. A Luggin capillary containing KNO3 was used to connect the reference electrode with the cell. All the electrochemical experiments were performed using an Electrochemical Analyzer (CH Instruments Model 604C). The temperature was maintained at 30 °C using a thermostat.
Ethanoic acid was first standardized titrimetrically and solutions of concentrations 1, 2.5, 5, 10, 20, 40 and 80% (by volume) were prepared. Aqueous ethanoic acid of concentration 20% was found most corrosive to steels [24]. Therefore, to investigate the effect of chloride ions on the corrosion behavior of stainless steels, experiments were carried out in different concentrations of NaCl ranging from 0.01 to 0.5 M in 20% ethanoic acid.
Electrochemical experiments
All the electrochemical experiments were carried out in the electrochemical cell containing 150 mL of unstirred test solutions without deaeration. At the beginning of each experiment, the open circuit potential (ocp) was allowed to reach an approximately constant value by performing potential versus time experiment. When the rate of variation in potential is less than 5 mV/h, the ocp is considered to be attained [25]. It took 3-6 hours to attain a stable ocp depending upon the composition of the electrolyte. After attainment of ocp, potentiodynamic polarization curves were obtained in the range of -0.4 to +1.8 V at a scan rate of 1 mV s-1. The ac impedance measurements were carried out at different potentials selected on the basis of polarization curves. A frequency range of 0.005 to 105 Hz and amplitude of 0.005 V was selected. The system was subjected to a hold time of 1 h at a particular potential prior to impedance measurements. All the experiments related to corrosion studies were repeated for four times. The mean values of the parameters is recorded in tables 1-5 and considered for analysis and discussion.
Table 1. Effect of exposure duration on the impedance measurements of AISI 316 in 20% acetic acid at 30 °C, 0.6 V and 1 mV s-1scan rate.
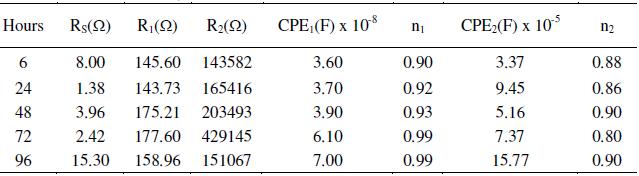
Table 2. Effect of concentration of acetic acid on the impedance measurements of AISI 316 at 30 °C, 0.6 V and 1mV s-1 scan rate.
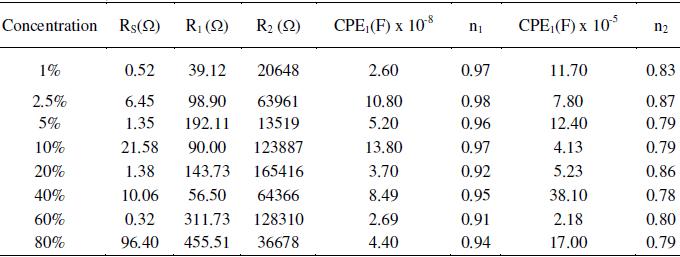
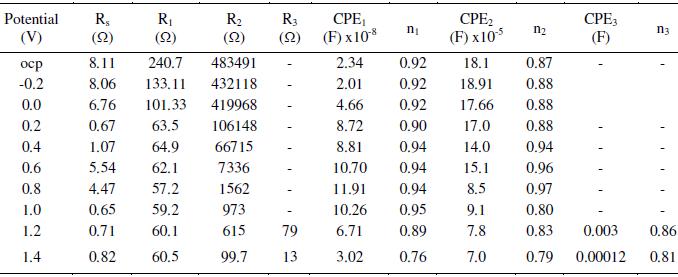
Table 3. Effect of applied electrode potential on the impedance measurements of AISI 316 in 20% acetic acid at 30 °C and 1 mV s-1 scan rate.
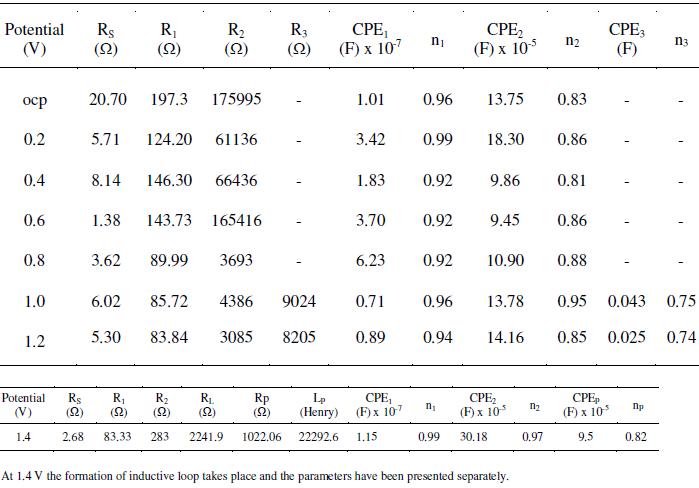
Table 4. Effect of salt concentration on the impedance measurements of AISI 316 in 20% acetic acid at 30 °C, 0.6 V and 1mV s-1 scan rate.
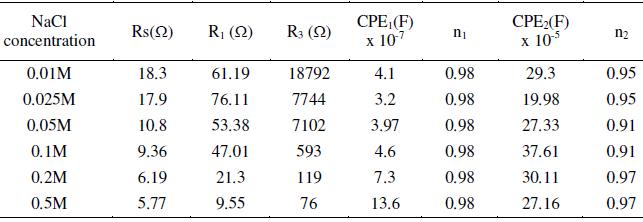
Table 5. Effect of applied electrode potential on the impedance measurements of AISI 316 at 30 °C in 20% acetic acid containing 0.4 M NaCl.
Determination of impedance parameters
We have used our own algorithm implemented on Mathematica 7.0 to determine circuit parameters rather than using the ones reported in the literature for computing the circuit parameters. This gives us a better handle to restrict to a single (or few) circuit(s) for fitting to many data sets. We chose the goodness of fit (χ2) to be
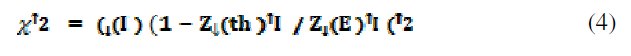
in place of the conventional chi square parameter. Here, Zth and ZE denote the theoretical and experimental value of the impedance and index 'I' runs over all the data points. This is because our impedance data vary over many orders (101 to 104). Moreover, the percentage errors occurring at higher orders weigh much more compared to those occurring for lower values of impedances. So, we first calculated the difference between unity and the ratio of theoretical value of impedance versus that obtained from the experimental data. Then we took the goodness of fit to be the sum of squares of the absolute values of these differences. In other words, we computed the distance in complex impedance plane between the experimental value of impedance and its theoretical value for a given set of circuit parameters. The goodness of fit of a statistical model describes how well it fits a set of observations. Measures of goodness of fit typically summarize the discrepancy between observed values and the values expected under the model in question. Goodness of fit is a method to measure the error in curve fitting. A lower value of chi-square reflects better fitting of the data.
We then normalized this distance by dividing it with the experimental data and calculated its difference from unity. This was followed by computing the sum of square of the absolute values of the differences between theoretical and experimental values to obtain goodness of fit parameter as stated in Eq. 4 (Fig. 3). After that, we determined the circuit parameters by minimizing the above mentioned goodness of fit parameter using Wolfram Mathematica 7.0. The corresponding program takes much less evaluation time if the iterative process to adjust the CPE exponent(s) is done manually rather than allowing the program itself to do so. Such a procedure seems to give much better fitting (as seen by eye) of the curves in impedance plots. The Nyquist and Bode plots were fitted by fixing the circuit parameters into the impedance equation in the programming steps. The program was run over 20 to 500 iterations with different CPE exponents in order to minimize the goodness of fit and get maximum fitting. In the end, program yields results in the form of circuit parameters viz., solution resistance (Rs), charge transfer resistance (Rt), non ideal capacitance in terms of constant phase element (CPE), CPE exponent and inductance (L).
Results and discussion
Polarization curves of AISI 316 obtained in aqueous ethanoic acid of concentrations ranging from 1-80% are shown in Fig 1(a). The curves show typical behavior with a small active region followed by a well defined passive, transpassive and secondary passive regions. The passive region extends from 0.2 to 1.0 V. After addition of different amounts of NaCl to 20% ethanoic acid, the Ecorr shifts towards negative direction and the passive region becomes successively smaller with the increase in the concentration of NaCl in test solution. A well defined pitting potential is also obtained, which indicates initiation and propagation of pits on the steel surface (Fig. 1(b)). In the present communication, potential points corresponding to the different regions on the Tafel's plots of the steel in 20% ethanoic acid and the latter containing 0.4 M NaCl are selected (indicated by marked spots in Figs. 1(a) and (b)) for ac impedance measurements. The observed plots in the impedance measurements were indeed the arc of a circle, but with its center below the x-axis. The results are discussed under the following sections.
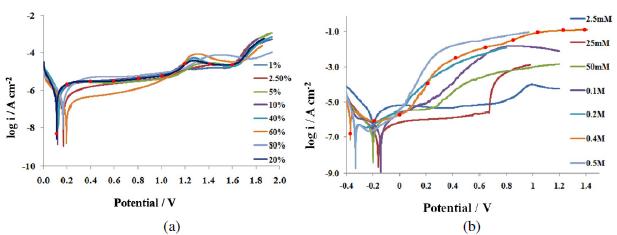
Figure1. Potentiodynamic polarization curves obtained for AISI 316 after 24 h of immersion under static conditions in (a) 1-80% aqueous ethanoic acid and 20% acid is marked at certain potential points selected for impedance investigation, and (b) after adding different amounts of NaCl ranging from 2.5 mM to 0.5 M to 20% ethanoic acid and the polarization curve of the steel in 20% ethanoic acid containing 0.4 M NaCl is marked at certain potential points for impedance analysis.
Effect of exposure time
To study the effect of exposure time on the surface film properties of the steel, an applied potential of 0.6 V (passive region) was selected. The reason behind is to make a comparative study of results obtained in ethanoic acid containing chloride ions (discussed in section 3.4) as pitting corrosion process takes place in the passive potential range. Nyquist plots (Fig. 2(a)) show the formation of depressed semicircular capacitive loops owing to surface heterogeneity.
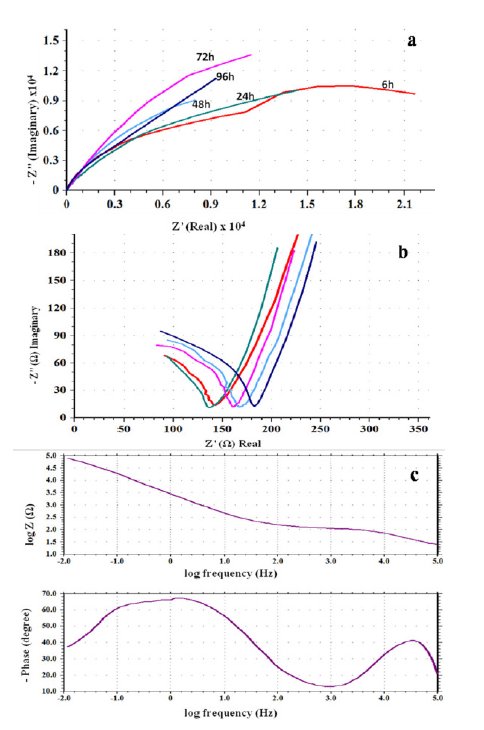
Figure 2. Effect of exposure duration on impedance measurements (a) Nyquist overlay plots, (b) capacitive loops formed in the high frequency region of the Nyquist plots, (c) Bode plots viz., log Z/log freq. and Phase /log frequency.
This is caused by surface distribution of reaction rates with the locations on the electrode [26]. Such a phenomenon is common with passivating alloys. On moving towards the high frequency region of these plots, another capacitive loop becomes visible (Fig. 2(b)).
With increase in the exposure time, the arc of the capacitive loops increases in size, but the increase is not very significant. The arc obtained in the low frequency region after 6 h (hours) exposure was found more depressed compared to the arc at 24 h. The arc at 72 h is the least depressed. The change in the dimension of the capacitive arcs indicates that the state of adsorptive intermediate changes with time. Sekine et al. [27] have reported the formation of [M(CH3COO)m]ad or [M(OH)n]ad on the surface of AISI 316 SS during this process.
Because of the inherent limitation in the impedance data interpretation (different circuits may yield the same spectrum), only the simplest possible equivalent circuits were used for spectra fitting. Simulations were carried out with the help of Eq. 5 (Fig. 7(a)), incorporating the circuit elements shown in Fig. 3. A comparison between the measured and simulated spectra using fitting algorithm is presented in Fig. 4. It is preferred that the circuit chosen for the fitting of spectra be simple, convenient and capable to explain maximum number of plots. Barring a few cases (e.g., 4(b)), in most of the cases an excellent fitting was found (Fig. 4(a)). Even, the latter case can be regarded as acceptable considering the complexity of the passive film formed on the steel surface. In such cases, to fit the curves completely, inclusion of some more circuit elements would be required. With each curve, a variety of circuits would appear. The variation of circuit elements is so wide ranged that it led to over fitting, thereby making the analysis very cumbersome and complicated. Over fitting generally occurs when a model is excessively complex, such as having too many parameters relative to the number of observations. A model which has been over fit will generally have poor predictive performance, as it can exaggerate minor fluctuations in the data. This was the reason we used our own algorithm for analyzing the results.
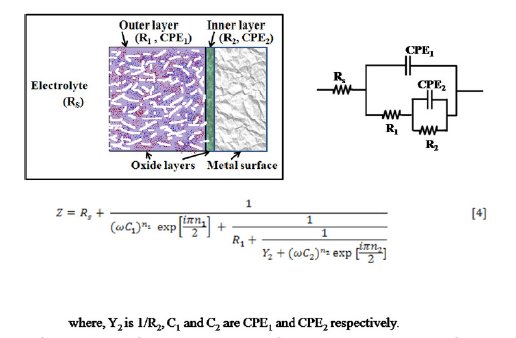
Figure 3. Model of passive film structure formed on the surface of AISI 316 and equivalent electrical circuit.
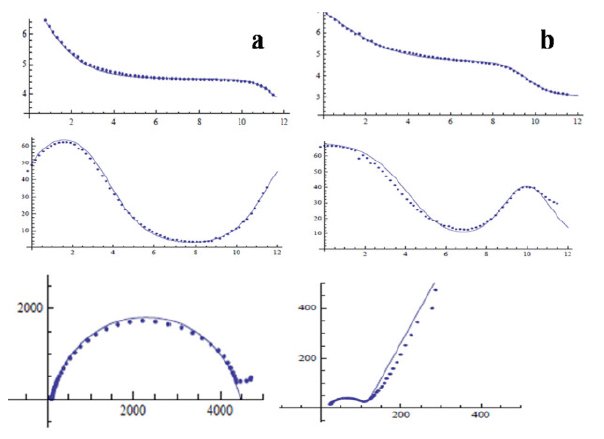
Figure 4. Comparison between measured and simulated spectra. Dotted lines represent measured spectra and solid lines represent simulated spectra. (a) Good fitting and (b) reasonably moderate fitting.
When the metal samples with protective passive films are exposed to a non aggressive electrolyte, i.e., ethanoic acid, the impedance response is determined essentially by the resistive and capacitive properties of the surface film. Bode plots give more clear picture (Fig. 2(c) exhibiting two humps or peaks corresponding to the two capacitors (CPEs), and the three depressions corresponding to three resistors in the circuit [26]. For deducing the equivalent circuit, fitting and simulation, both Nyquist and Bode plots have been utilized. To explain these plots, we suggest a simple model in Fig. 3. It displays metal surface with a two layered passive film structure and the equivalent circuit with five elements. The total impedance (Z) can be calculated using Eq. 5 (Fig. 7(a)). The numerical values of the circuit elements are recorded in Table 1. Depending on whether the film has a single or multilayer structure, the spectra over a wide frequency range may exhibit one or more time constants because of film resistance or capacitance. The capacitive loop in the high frequency region represents the electric charge transfer process. The second capacitive loop at intermediate frequencies is attributed to adsorption-desorption processes (of intermediates), and the third capacitive loop in the low frequency region is associated to a diffusion processes through corrosion products inside the pits/cracks. The third capacitive loop is obtained during impedance measurements at higher potentials (1.0 to1.6 V) and also when chloride ions were added to the medium (section 3.4).
For the ac impedance experiments under this section, we report the formation of two capacitive loops corresponding to charge transfer process (capacitive loop in the high frequency region) and diffusion process (loop in the low frequency region). The complex plane shows a wide semi-circle at low frequencies and a small semi-circle at higher frequencies which becomes further small at higher potential (Fig. 2(a) and (b)). This is attributed to the difference in the structure and properties of the inner and outer layers of the passive film.
The measured capacitive response was not found to be of ideal capacitor. This deviation is incorporated by utilizing a constant-phase element (CPE) for spectra fitting, instead of an ideal capacitance element (Cdl). R1 is referred to the resistance of the porous layer since it continuously bathes in the electrolyte solution. It is also considered as resistance of the solution inside the pores of the film [28]. It strongly depends on the defective structure (porosity) of the film. R2 and R3 are resistances of the compact portions (inner layers) of the passive film.
As the exposure duration was increased up to 72 h, the resistance of the outer layer increases, but not significantly. This indicates thickening of the outer layer and the film retains its protective ability. In some literature, it has been reported that the increase in film resistance and the decrease in film capacitance with time indicate the growth and formation of compact passive film [29, 30]. As the surface film grows, different transport mechanisms take place in the inner and outer parts of the film. Additionally, the internal redox reactions also play crucial role in the formation of a multilayered passive film. The composition of the inner and outer layers may vary in different cases. The inner layer is generally more continuous and almost non-conducting (high resistance values), whereas the outer layer is relatively porous (comparatively lower resistance values). In the present investigation, the outer layer capacitance (CPE1) has been found to increase with the length of exposure, which suggests that the oxide film has further thickened. On increasing the exposure duration from 72 to 96 h, the resistance of the inner and outer layers and thus overall film resistance decreases, indicating that along with thickening, the film also becomes more defective. This probably is due to the generation of pores, channels or cracks in the passive film. From these results, it is apparent that extended immersion hours inside the electrolytic solution (ethanoic acid) leads to the growth of a defective or porous surface film. In this investigation, the main feature of the impedance response, i.e., two time constants observed in the spectra of most specimens, is likely due to the two layered structure of the passive films. The CPE powers (n1 and n2) range from 0.86-0.99. This suggests occurrence of little or no considerable roughness on the surface. However, the pristine shine of the surface was lost.
Effect of concentration of ethanoic acid
Fig. 5(a) shows Nyquist overlay plots of AISI 316 obtained after 24 h in different concentrations of ethanoic acid ranging from 1 to 80% at an applied potential of 0.6 V and 1 mV s-1 scan rate. The capacitive loops formed in the high frequency region for the same are shown in Fig. 5(b). The semicircular loops in the low frequency region are depressed owing to surface heterogeneities. On the other hand capacitive loops formed in the high frequency region are somewhat less depressed. This indicates that the inner surface film is compact and continuous providing good protection. This is further supported by high R2 (104 - 105 Ω) and n values (0.9-0.8). The circuit parameters are displayed in Table 2. If the passive layer grows uniformly, the resistance increases and capacitance decreases in proportion to the increase in the thickness of the film. But in the present case, the circuit parameters in different concentrations of ethanoic acid are scattered and there appears no correlation. This is not surprising because of the fact that the impedance study was carried out at an applied potential in the passive region and not at Ecorr. Hence, it is inferred that, the formation, structural nature and properties of the passive film on the steel surface, is independent of the acid concentration. The structure and properties of the passive film in this case can be explained using the model and equivalent circuit given in Fig. 3.
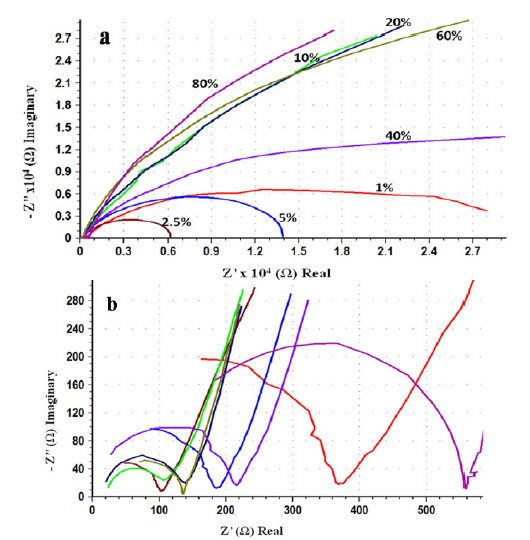
Figure 5. Effect of concentration of ethanoic acid on the impedance measurements of AISI 316. (a) Nyquist overlay plots and (b) capacitive loops of the same in the high frequency region.
During the corrosion process of stainless steels in acidic electrolyte, the composition, structure, and morphology of the passive film vary with composition and time [28]. The dielectric constant may change according to the variation in the film composition and structure. The effective area may also increase significantly due to an increase in the surface roughness. In particular, the resistivity may vary since it depends strongly upon the defective structure of the passive film. If interconnecting pores, channels, or cracks are formed inside the oxide film, they affect many properties of the film. Impedance of the whole layer can be calculated using equivalent circuit based on the surface film (oxide layer) model given in Fig. 3, but the details of individual pores, channels, or cracks cannot be obtained. The total effect of pores, channels, or cracks on the impedance response is reflected in the parameters of the outer layer (R1, CPE1 and n1) and possibly also in R2 when the defects extend into the barrier layer. R1 is a measure of general corrosion rates, but alone it is inadequate to characterize uniform or localized corrosion. The surface roughness caused by corrosion increases the real surface area and double layer capacitance, while decreasing n. Although the coefficient n by itself suffices as a roughness indicator, a combination of R1 and n gives more valuable information for the classification of corrosion patterns. An accelerated corrosion decreases charge transfer resistance and increases surface roughness. Hence both R1 and n decrease simultaneously. In the event of severe localized corrosion, low values of R1 and n are expected. When corrosion is subdued by uniform coverage of a passive film, as in the present case, both R1 and n are high. This suggests that the surface is not affected due to insignificant corrosion.
Effect of applied potential
Nyquist plots obtained for AISI 316 at different applied potentials are shown in Fig. 6(a) and (b). The corresponding Bode plots are displayed in Fig. 6(c) and this represents complete picture for the changes in the spectra on increasing the applied potential. Since, different physio-electrochemical reactions take place over the steel surface corresponding to different regions on the Tafelâs plot; therefore, successive change in the shape of each capacitive loop with potential is visible in the diagram.
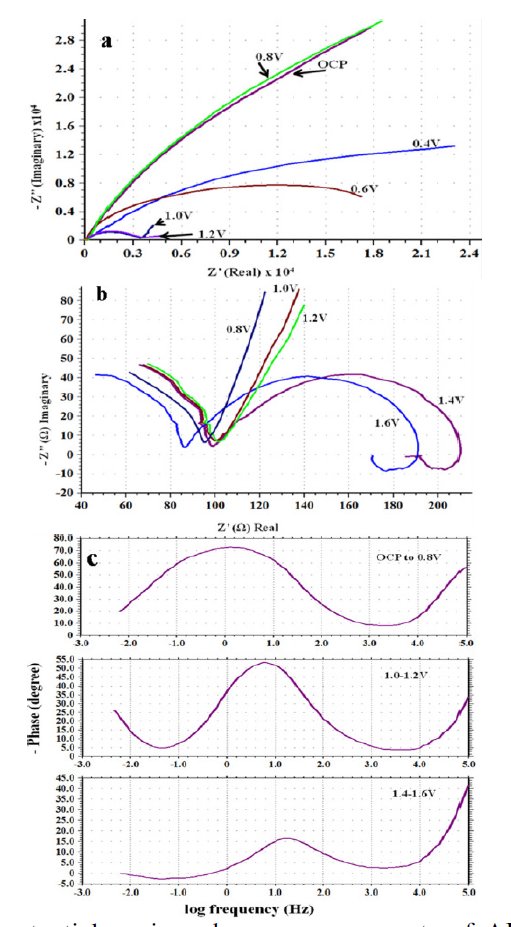
Figure 6. Effect of potential on impedance measurements of AISI 316. (a) Nyquist overlay plots; (b) capacitive loops in the high frequency region of the Nyquist plots; and (c) Bode plots (Phase/log frequency).
In the low potential region (ocp to 0.8 V), there are only two humps or peaks (Fig. 6(c)). These correspond to three resistors and two capacitors. The process can be explained by the model shown in Fig. 3. When the potential was increased from 1.0 to 1.2 V, there appeared one more peak. It corresponds to the introduction of a third capacitor in the equivalent circuit. There are now three time constants in the equivalent electrical circuit as given in Fig. 7(a). The total impedance can be calculated using Eq. 6 (Fig. 7b). On further increasing the potential from 1.4 to 1.6 V, inductive loop in the low frequency region is formed which appears in the fourth quadrant. In the Bode plot, this phenomenon appears as a low frequency tail creeping below zero or negative quadrant Fig. 6(c). This is due to the formation of adsorbed intermediates on the steel surface. To explain the inductive loop formation in the case of AISI 316 (Fig. 6(b) and (c)) in single attempt, the circuit becomes complicated. In order to simplify it, the circuit was divided into two parts (Fig. 7(b)). For programming and simulation, the experimental text data of the Nyquist and Bode plots were divided into two parts and it was found that the algorithm for the above mentioned circuits runs successfully.
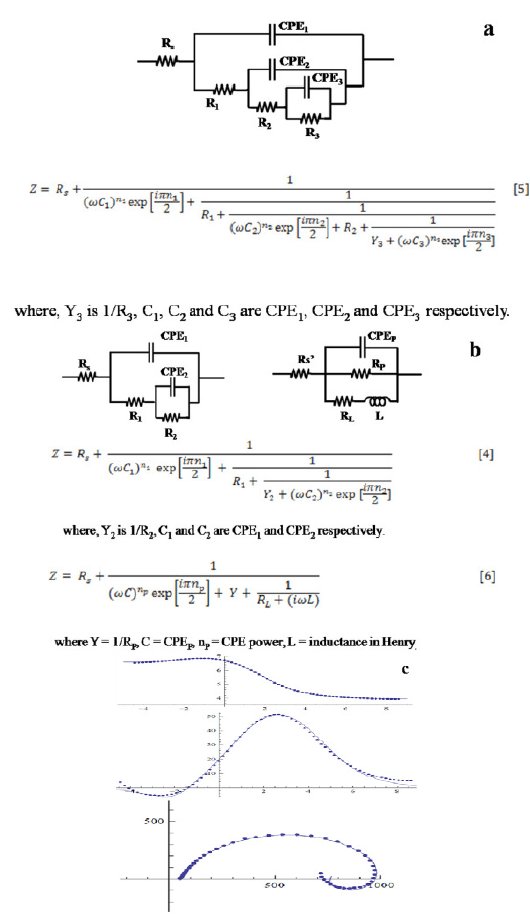
Figure 7. (a), (b) Combination of equivalent circuits to explain the Nyquist and Bode plots of AISI 316 obtained at 1.4-1.6 V, and (c) comparison between measured and simulated spectra.
The comparison of measured and simulated spectra is shown in Fig. 7(c). The total impedance can be calculated by taking together the individual impedances at different frequencies obtained from Eqs 4 and 6. It can be considered that the corrosion process taking place in the high frequency region resembles to the model and equivalent circuit given in Fig. 3. Whereas, the process taking place in the low frequency region differs from the former and follows a different pathway involving formation of adsorbed intermediates on the surface. The inductance is interpreted as originated mainly from the adsorption of the intermediates (possibly Fe (CH3COO)ads). The parameters are displayed in Table 3. In this case, when the inductive loop is not formed (i.e., 1.0 to 1.2 V), the number of circuit elements increases to ten. It increases to twelve when inductive loop is there (at potential 1.4 to 1.6 V). Due to large number of variables in the curve fitting, it usually takes long hours to run it and the proper fitting becomes cumbersome. Therefore, this complicated circuit was divided into two simple circuits for the fitting and simulation purposes.
R1 arises due to the anodic interfacial process, possibly the charge transport through the surface oxide layer and the rate of which is known to be independent of the potential in a wide range. As a result, it remains almost constant in these potential ranges. The composition of the metal phase changes during active dissolution. This is responsible for a variation in R1 values. The passive film formed on the surface governs the major part of chemical reactions occurring on the surface. This controls the dissolution rate, overpotentials, enrichment of alloying elements on the surface and provokes repassivation. Evidences of enrichment of the alloying elements on the surface of steels have already been reported by many workers. The passive films of AISI 316 were found to be composed of a complex oxide and oxyhydroxide containing Cr3+, Fe3+, Ni2+, Mo4+ and Mo6+ ions. An increase in the thickness of the passive film with increase in Mo content has been reported by Olefjord et al. [31]. By the virtue of the alloying elements, there occurs formation of multi-layered passive film on the surface. A two-layered film formed in the potential range of ocp to 0.8 V is reflected in two CPEs in the equivalent circuit. Similarly, a three-layered film formation in the potential range 1.0 to 1.6 V is reflected in three CPEs in the equivalent electrical circuit. The impedance study reveals that the corrosion phenomenon occurring in the stainless steel-ethanoic acid systems is very complex because of the formation of multiple passive layers on the surface.
Effect of chloride ion addition
Impedance measurements were carried out in 20% ethanoic acid containing different quantities of NaCl at 30 °C after exposure duration of 24 h. Nyquist plots were depressed semicircles with their center below the axis. Bode plots show typical double peak features which indicate that the process involved two CPEs. The parameters calculated using Eq. 5 are recorded in Table 4. From the data, it is evident that the R1 and R2 values are lower compared to those in Tables 1-3. This indicates that the presence of chloride ions increases the conductivity of the medium, and invades into the passive film to enhance its defects. The film now contains more cracks, pores and channels. If defects are present inside the passive film, the electrolyte will penetrate into the film and attack the surface at the sites where the film is thin and weak. This leads to a decrease in the electrical resistance.
In order to study the effect of applied potential on the corrosion process in the presence of chloride ions, impedance measurements were carried out in 20% ethanoic acid containing 0.4 M NaCl. The features of Nyquist plots obtained in the potential region ocp to 1.0 V resembled to that shown in Fig. 5, i.e., formation of two capacitive loops. At potentials 1.2 and 1.4 V, little different behavior was obtained due to the formation of three capacitive loops (Fig. 8). This seems to be a well-developed complex diagram, but a closer examination reveals a good RC behavior for high frequencies followed by a progressively inductive behavior towards the lower frequency part of the diagram. This apparent inductive loop is caused by relatively slow changes in the specimen properties, in contrast with the fast changes due to the breakdown of passivation film. The n values close to unity show that the surface is very little affected due to the pitting corrosion caused by the presence of chloride ions. It was observed while comparing the n values in the passive region (Tables 3, 4 and 5), that in the absence of chloride ions, the values fall in the range 0.81 to 0.96 at potentials 0.4, 0.6 and 0.8 V. After addition of chloride ions, the n values fall in the range 0.94 to 0.96 at similar potential inputs. This indicates that the surface heterogeneity or roughness in the latter case is less.
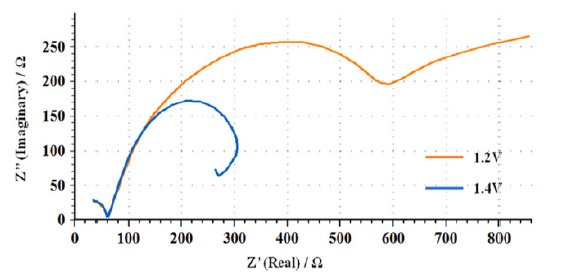
Figure 8. Overlay of Nyquist plots of AISI 316 in 20 % ethanoic acid containing 0.4 M NaCl at 1.2 and 1.4 V.
This can be explained in terms of alloy composition of the steel in which, besides Ni and Cr, 3-4 % molybdenum is also present. The role of Mo in passivation process has been reported by many researchers. Apart from resistance to pitting, Mo facilitates the process of repassivation as well. Once the pits are formed over the surface, the active sites are rapidly covered with molybdenum oxyhydroxides or molybdate salts, thereby inhibiting localized corrosion [31]. When passive film grows, the oxide lattice is dominated by multiple valent species (ions) of Cr and Fe which combine to produce point defects. These defects are possibly cancelled by the presence of 4-and 6-valent Mo species and the film becomes less defective. This makes the passive film less prone to be penetrated by aggressive anions (such as chloride ions in the present case). Thus, Mo reduces the chances of chloride ion invasion into the passive film. Studies show that chloride ion content in the passive film of Mo free alloys is considerably higher than Mo containing alloys [32]. It is further suggested that the mechanism for lowering of the chloride ion content in the film is due to the ability of Mo to form soluble stable Mo-oxo-chloro complexes [33]. The formation of these complexes, during the passivation process, lower the chloride ion content in the passive film, thereby making the film more resistant to pitting corrosion. Mo assists in repassivation process as well. Soon after the initial dissolution of Mo takes place, the protective chloride salt film stabilized by ferrous molybdate is eventually precipitated from the test solution. This insoluble chloride complex settles at the base of pits, thereby arresting chloride ions in the pit and forbids its invasion into the passive film. This, in turn, enables subsequent repassivation to occur. Hence, the corrosion resistance property of AISI 316 is improved in the aggressive media.
Conclusions
The formation, structure and properties of the passive film, changes with exposure duration, concentration of the ethanoic acid, applied electrode potential and concentration of chloride ion. Results show that the passive film formed on AISI 316 surface is multilayered and possesses dual structure. The film is made up of a thin and compact internal part, and a thicker, porous external part. Extended immersion hours inside the electrolytic solution (ethanoic acid) leads to the growth of a defective or porous surface film. The formation, structure and properties of the passive film are independent of the acid concentration. At passivating potential ocp to 0.8 V, there is the formation of two capacitive loops, and at higher potential input (1.0-1.2 V), formation of three capacitive loops takes place. At higher potentials (1.4-1.6 V), the formation of an inductive loop takes place owing to adsorbed intermediates. The capacitive behavior is of non ideal nature and it is explained in terms of constant phase element. The CPE power or n values show that surface roughness due to corrosion process becomes less in 20% ethanoic acid containing 0.4 M NaCl than in absence of the latter, owing to the repassivation role played by molybdenum and enabling the steel to behave more resistant to pitting corrosion in aggressive medium.
References
1. D.D. Macdonald, "Application of electrochemical impedance spectroscopy in electrochemistry and corrosion science", in: R. Varma, J.R. Selman (Eds.), "Techniques for Characterization of Electrodes and Electrochemical Processes", John Wiley & Sons, NY, (1991). pp. 515-647. [ Links ]
2. I. Epelboin, C. Gabrielli, M. Keddam, K. Takenouti, "The study of the passivation process by the electrode impedance analysis", in: J.O'M Bockris, B.E. Conway, E. Yeager, R.R.White (Eds.), "Comprehensive Treatise of Electrochemistry", Vol. 4, "Electrochemical Materials Science", Plenum Press, NY, (1981). pp. 151-188. [ Links ]
3. C. Gabrielli, "Identification of electrochemical processes by frequency response analysis", Technical Report 0004/83, Solartron Instruments (1984). pp. 53-72. [ Links ]
4. P. Marcus, V. Maurice, "Structure of thin anodic oxide films formed on single-crystal metal surfaces", in: A. Wieckowski (Ed.), "Interfacial Electrochemistry-Theory, Experiment and Application", Marcel Dekker Inc., NY, (1999). pp. 541-558. [ Links ]
5. A.M. Nagiub, Port. Electrochim. Acta 23 (2005) 301-314. [ Links ]
6. J.B. Jorcin, M.E. Orazem, N. Pebere, B. Tribollet, Electrochim. Acta 51 (2006) 1473-1479. [ Links ]
7. J. Flis, Y.Tobiyama, K. Mochizuki, C. Chiga, Corros. Sci. 39 (1997) 1757-1770. [ Links ]
8. A. Jimenez-Morales, J.C. Galvan Rodriguez, J.J. De Damborena, J. Appl. Electrochem. 27 (1997) 550-557. [ Links ]
9. M.A. Ameer, M.A. Fekry, F. El-Taib Heakal, Electrochim. Acta 50 (2004) 43-49. [ Links ]
10. S.S. El-Egamy, W.A. Badaway, H. Shehata, Mat-wiss. u. Werkstofftech. 31 (2001) 737-744. [ Links ]
11. B. Cox, Y.M. Wong, J. Nucl. Mat. 218 (1995) 324-334. [ Links ]
12. M.A. Martini Emilsce, L. Muller Iduvirges, Corros. Sci. 42 (2000) 443-454. [ Links ]
13. I. Epelboin, M. Keddam, H. Takenouti, J. Appl. Electrochem. 2 (1972) 7179. [ Links ]
14. D.R. MacFariane and S.I. Smedley, J. Electrochem. Soc. 133 (1986) 2240-2244. [ Links ]
15. D.C. Silverman, Corrosion NACE 45 (1989) 824-827. [ Links ]
16. W.J. Lorenz, F. Mansfeld, Corros. Sci. 21 (1981) 647-672. [ Links ]
17. M.J. Kendig, J. Electrochem. Soc. 131 (1984) 2777-2779. [ Links ]
18. R.D. Armstrong, M. Henderson, J. Electroanal. Chem. and Interfac. Electrochem. 39 (1972) 81-90. [ Links ]
19. I. Epelboin, M. Keddam, J. Electrochem. Soc. 117 (1970) 1052-1056. [ Links ]
20. F. Mansfeld, Corrosion, NACE International 36 (1981) 301-307. [ Links ]
21. S.M. Gerchakov, L.R. Odey, F. Mansfeld, Corrosion, NACE International 37 (1981) 696-703. [ Links ]
22. F. Mansfeld, M.W. Kendig, Workstoff und Korrosion 34 (1983) 397-401. [ Links ]
23. M.W. Kendig, E.M. Meyer, G. Lindberg, F. Mansfeld, Corros. Sci. 23 (1983) 1007-1015. [ Links ]
24. N. Mahato, "Corrosion and pitting behavior of austenitic stainless steels in ethanoic acid containing chloride ions", Ph.D. thesis in Applied Chemistry, Banaras Hindu University, Varanasi (2010). [ Links ]
25. R.G. Kelly, J.R. Scully, D.W. Shoesmith, R.G. Buchheit, "Electrochemical Techniques in Corrosion Science and Engineering", Marcel Dekker Inc., NY (2003). [ Links ]
26. G.W. Walter, Corros. Sci. 26 (1986) 681-703. [ Links ]
27. I. Sekine, A. Masuko, K. Senoo, Corrosion NACE International 43 (1987) 553-560. [ Links ]
28. J. Pan, C. Leygraf, R.F.A. Jargelius-Pettersson, Linden, Oxidation of Metals 50 (1998) 431-455. [ Links ]
29. A. Baltat-Bazia, N. Celati, M. Keddam, H. Takenouti, R. Wiart, Mat. Sci. Forum 111 (1992) 359-368. [ Links ]
30. N. Celati, S Catherine, M. Keddam, H. Takenouti, Mat. Sci. Forum 192 (1995) 335-344. [ Links ]
31. I. Olefjord, B. Brox, U. Jelvestam, J. Electrochem. Soc. 132 (1985) 28542861. [ Links ]
32. L. Wegrelius, F. Falkenberg, I. Olefjord, J. Electrochem. Soc. 146 (1999) 1397-1406. [ Links ]
33. J.R. Ambrose, "Passivity of Metals", (R. P. Frankenthal and J. Kruger, eds.), Electrochem. Soc., Pennington NJ (1978). p. 740. [ Links ]
*Corresponding author. E-mail address neelapchem@gmail.com
Received 14 February 2011; accepted 8 June 2011
Acknowledgements
Authors are pleased to thank Dr. Manavendra Nath, Department of Theoretical Physics, Tata Institute of Fundamental Research, Colaba, Mumbai, for fruitful discussion. Research grant (Senior Research Fellowship) provided by UGC-India to one of the authors is gratefully acknowledged.