ARTÍCULOS

Mapeos Proyectivos: la base para el Funcionamiento del Pizarrón Interactivo WiimoteWhiteboard

Projective Mapping: the base function of the WiimoteWhiteboard

 

Sodel Vázquez-Reyes ¹, Juan L. Villa-Cisneros ², José E. Anaya-Villagrana ³, Fernando J. Barrera-Ambriz ⁴, María de León-Sigg ⁵ y Carlos H. Casteñeda Ramírez⁶

¹ Profesor Investigador de la UAZ, Edificio de Ingeniería en Computación y Software, 1er Piso. Carretera a Guadalajara Km 6, Ejido la Escondida., 98160, Zacatecas, México. E-mail: vazquezs@uaz.edu.mx

² Profesor Investigador de la UAZ, Edificio de Ingeniería en Computación y Software, 1er Piso. Carretera a Guadalajara Km 6, Ejido la Escondida., 98160, Zacatecas, México. E-mail: jlvilla@uaz.edu.mx

³ Egresado de Ingeniería en Computación (UAZ), patrocinio 118, col. centro, 98000, Zacatecas, Zac.E-mail: gran_ed@hotmail.com

⁴ Egresado de Ingeniería en Computación (UAZ), patrocinio 118, col. centro, 98000, Zacatecas, Zac. E-mail: fer_kail@hotmail.com

⁵ Profesor Investigador de la UAZ, Edificio de Ingeniería en Computación y Software, 1er Piso. Carretera a Guadalajara Km 6, Ejido la Escondida., 98160, Zacatecas, México. E-mail: melonsigg@uaz.edu.mx

⁶ Profesor Investigador de la UAZ, Edificio de Ingeniería en Computación y Software, 1er Piso. Carretera a Guadalajara Km 6, Ejido la Escondida., 98160, Zacatecas, México. E-mail: castr@uaz.edu.mx

 

RESUMEN

En la actualidad han surgido diversos proyectos que se enfocan en la implementación de pizarrones interactivos de bajo costo usando el control Wii como principal componente. Sin embargo, aunque hay una gran cantidad de información acerca de estos proyectos y de cómo implementar este tipo de pizarrones, el funcionamiento que hay detrás de este proyecto aun no es muy conocido. En este artículo, se describe el algoritmo base para la implementación de este tipo de pizarrones, el cual está basado en transformaciones proyectivas, usando una matriz de Homografía.

Palabras-clave: Homografía, pizarrón interactivo y operaciones de matriz.

 

ABSTRACT

Nowadays, many emerging projects focus mainly in developing low cost interactive whiteboards, having the Wiimote as their main working tool. However, although there is a lot of information about these projects and how to implement these interactive whiteboards, only few people know how this project really works. This article describes the base algorithm of the low cost interactive whiteboards, which is based in projective transformations, using a homography matrix. The implementation of this technology in Mexican educative institutions could reinforce learning processes at all levels, without the need to spend too much. This is a collateral advantage of information technology re-engineering.

Keywords: homography, interactive board and matrix operations.

 

1.  Introducción

Uno de los recursos didácticos más innovadores para la impartición de clases son los pizarrones interactivos, los cuales pueden ser catalogados como táctiles o resistivos, electromagnéticos, ultrasónicos-infrarrojos e infrarrojos. No obstante a pesar de ser un recurso didáctico novedoso, su alto costo comercial, los convierte en una herramienta prácticamente inaccesible para la mayoría de las personas y sobretodo para la gran mayoría de las instituciones educativas.

Por esta razón, surgió un pizarrón de tecnología infrarroja conocido como WiimoteWhiteboard, el cual usa un control Wii como cámara infrarroja, para detectar la posición de la pluma Infrarroja (IR). Hoy en día existe una gran variedad de pizarrones que hacen uso del control Wii, con diferentes variaciones en la funcionalidad como es el soporte de varios controles, portabilidad en varios sistemas operativos, reconocimiento del doble clic y diferentes configuraciones del mouse. También existen sitios en la web, donde explican cómo montar un pizarrón de este tipo y qué componentes se requieren, sin embargo, en ninguno de estos sitios se explica cómo es que este pizarrón funciona.

Es por esto que se decidió analizar los trabajos actuales hechos sobre este pizarrón y crear un algoritmo que permita entender el funcionamiento del pizarrón, para poder implementarlo en cualquier lenguaje de programación. Una vez logrado esto, será posible que las personas, desarrollen sus propios pizarrones interactivos con características y funcionalidades propias, en lugar de utilizar software de terceros que podrían no ajustarse a sus necesidades.

 

2. Marco de Referencia

El primero que usó el control Wii como sensor para crear un pizarrón interactivo fue Johnny Chung Lee, cuando desarrolló en el lenguaje de programación C#, la aplicación WiimoteWhiteboard en Junio de 2008 (Lee, 2012). Mediante el uso de esta aplicación y un control de la consola Wii, logró usar cualquier proyección de computadora sobre una superficie táctil, y mover el cursor del ratón dentro de la computadora donde el usuario lo indicara con su pluma infrarroja en la proyección. Solamente se tenía que calibrar la imagen donde se quería usar la pluma y que el control Wii tuviera acceso al led IR de la pluma.

Para que Chung Lee pudiera realizar toda esta tarea, necesitaba la información enviada por el control Wii y almacenarla. Esta tarea la realizó Brian Peek, quien desarrolló la primera biblioteca llamada Wiimotelib (Jin, 2012), que permitía hacer uso de las funciones que ofrecía el control Wii. Peek logró leer la información del control Wii, así como la conexión y desconexión correcta del control para usar los datos del control Wii correctamente.

Desde la aparición de la biblioteca Wiimotelib y de la aplicación de WiimoteWhiteboard, muchos usuarios han desarrollado sus propias aplicaciones para convertir una proyección en un pizarrón interactivo tal y como lo hizo Chung Lee. Las más importantes son Wiimote Whiteboard for Java, creada por Uwe Schmidt (Peek, 2012), wiiBoardJ creada por Jan Markowski (Markowski, 2012) y Wiimote Smoothboard hecha por Goh Boon Jin (Schmidt, 2012).

 

3.   Geometría Proyectiva, Base de los Pizarrones Wiimote

Este trabajo está basado en el programa desarrollado por Uwe Schimdt, porque se buscó desarrollar un producto de software que fuera soportado por diferentes sistemas operativos, tales como, Linux, Windows y Mac OS. Al igual que en otros proyectos, Uwe Schimdt no explicaba como era el verdadero funcionamiento del control Wii en este tipo de pizarrones. El principal problema enfrentado fue que cuando el sensor IR o la cámara IR del control Wii detecta los puntos infrarrojos, está detectándolos en un plano totalmente diferente al que se tiene en la pantalla de la computadora.

Para poder hacer coincidir los planos de la pantalla de la computadora y el que es detectado por el control Wii, se tuvo que hacer análisis de la geometría proyectiva, la cual es el fundamento de la calibración del pizarrón. Cuando se calibra el espacio de trabajo, generalmente se coloca un punto en cada una de las 4 esquinas de la proyección, que son donde se tendrá que poner la pluma IR para que pueda hacer la calibración por medio de la cámara o sensor IR.

Para que el pizarrón pueda funcionar, hay que convertir el cuadrilátero irregular que detecta, a un cuadrado o rectángulo que representa el área de trabajo tal y como es, como se muestra en la Figura 1. Para lograr esto se hace el uso de transformaciones y homografías.

 

 

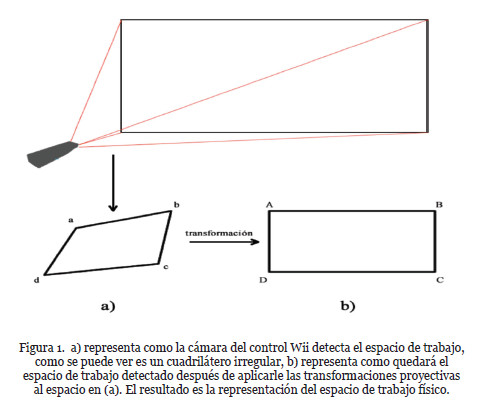
La transformación que se usa es conocida como mapeo 2D, el cual distorsiona un espacio origen 2D en un espacio destino 2D. Mapea un punto origen (x, y) a un punto destino (u, v), de acuerdo a las funciones x(u, v) y y(u ,v). Las clases más simples de mapeo 2D son las transformaciones afín, bilineal y proyectiva. La última es la que más interesa, ya que es la que la que se usará para la calibración del espacio de trabajo.

En la geometría proyectiva el punto real 2D (x, y) es representado por el vector homogéneo P=(x’, y’, w)=(xw, yw, w), donde w es un número arbitrario diferente de 0, ya que para poder recobrar las coordenadas actuales del vector homogéneo, simplemente se divide entre el componente homogéneo. En el caso del vector homogéneo P, representa el punto actual (x, y)=(x’/w, y’/w), si w=0, se dice que el espacio proyectivo tiene puntos que tienden a infinito, para este caso en particular, se iguala w=1, por conveniencia.

Para el mapeo o transformación proyectiva se denotan los puntos en el espacio origen con Ps=(x’, y’, q) y los puntos en el espacio destino con Pd=(u’, v’, w). Para realizar el mapeo entre el espacio origen y el destino, se hace uso de una matriz de transformación de 3x3 conocida como matriz de homografía, la cual es denotada normalmente como H y se representa en la ecuación 1.

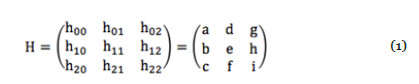
La manipulación de los mapeos proyectivos es representada por la ecuación 2, y su interpretación es más fácil si se pasa a la notación de matriz homogénea representada por la ecuación 3.

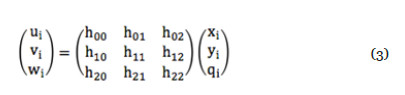
donde:

Pd es el plano destino, representado en forma de vector como (ui, vi,  wi)^T.

Msd=H que es la matriz de homografía.

Ps es el plano origen, representado en forma de vector como (xi, yi,  qi)^T.

Y(x, y)=(x’/q, y’/q) para q0 y

(u, v)=(u’/w, v’/w) para w0.

En este caso en particular se tomará un múltiplo escalar diferente de 0, por lo tanto sin perder generalidad podemos asumir que h₂₂=1 dándonos 8 grados de libertad en un mapeo proyectivo 2D.

Hay que poner la transformación en una forma más entendible, si se conocen los vectores (ui, vi,  wi)^T y (xi, yi,  qi)^T, entonces se tiene que calcular la matriz H, que es la que contiene las 8 incógnitas que se necesitan, por lo tanto, se obtienen las ecuaciones descritas en 4:

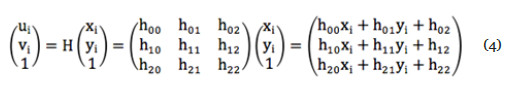
Entonces si en coordenadas homogéneas se tiene que ui’=ui/w y vi’=vi/w se tiene que w= , se obtienen las ecuaciones 5 y 6 para cada uno de los puntos (x,y) del plano origen al plano destino:

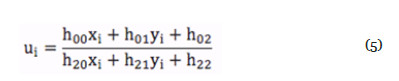
Las ecuaciones 5 y 6 corresponden a un solo punto (x,y), si se tienen 4 correspondencias de puntos para i de 0 a 3, entonces se pueden expresar estas ecuaciones en forma matricial de Ax=b quedando un sistema de 8x8, como lo muestra la ecuación 7.

Este sistema lineal puede ser resuelto usando el Algoritmo de Transformación Lineal Directa para la obtención de las coordenadas espaciales tridimensionales de un objeto (DLT), en caso de ponerlo como Ax=0, para los coeficientes h₀₀-h₂₁. Si el mapeo inverso es deseado en su lugar, entonces se puede calcular la matriz adjunta de H, pero en casos especiales de velocidad crítica como el caso que se presenta, hay fórmulas más eficientes para el cálculo de la matriz de transformación. En el uso de la fórmula 7, hay 3 casos a considerar: cuadrado a cuadrilátero, cuadrilátero a cuadrado y cuadrilátero a cuadrilátero, los cuales se pueden observar en la Figura 2.

 

 

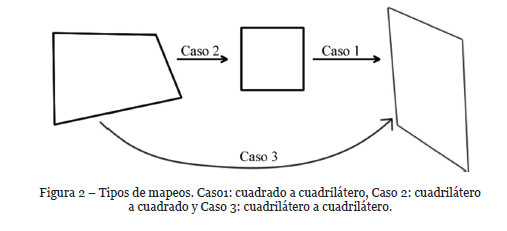
Caso 1: el sistema es fácilmente resuelto simbólicamente en el caso especial donde el cuadrilátero xy es un cuadrado unitario. Si la correspondencia de vértices de (u, v) a (x, y) es la siguiente:  (u0 ,v0) = (0, 0), (u1 ,v1) = (1, 0), (u2 ,v2) = (1, 1) y (u3 ,v3) = (0, 1). Al sustituir las x y y, en la ecuación (7) y despejando las incógnitas (,  y  quedan las siguientes 8 ecuaciones:

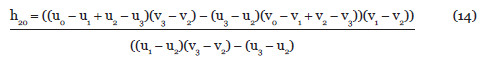
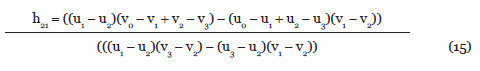
Caso 2: el mapeo inverso, de un cuadrilátero a un cuadrado, también puede ser optimizado, si se usan las ecuaciones de cuadrado a cuadrilátero que se acaban de describir (8 a 15) para encontrar la inversa del mapeo deseado y luego se toma su adjunta para calcular el mapeo de cuadrilátero a cuadrado, lo cual puede verse en la Figura 2, porque la inversa de un mapeo proyectivo es un mapeo proyectivo.

Caso 3: se pueden calcular los mapeos de un cuadrilateral a un cuadrado y de un cuadrado a un cuadrilateral rápidamente, los 2 mapeos pueden fácilmente ser compuestos, es decir, se multiplica la matriz del cuadrilátero a cuadrado por la matriz de cuadrado a cuadrilátero, para dar un mapeo de cuadrilátero a cuadrilátero.

Finalmente se pasaron los 3 casos anteriores a código en lenguaje Java, se creó una clase llamada TransformacionesProyectivas, la cual contiene 6 métodos, un constructor, sus correspondientes accesores y mutadores. Cada uno de los 6 métodos representa las principales operaciones matriciales que deben hacerse para el cálculo de la matriz de transformación, estos métodos son los siguientes:

• cuadroCuadrilatero: Este método representa el caso 1 de las transformaciones proyectivas, donde se mapea un cuadrado unitario en un cuadrilátero irregular arbitrario, recibe como parámetro una matriz bidimensional de 4x2 y regresa como resultado una matriz de 3x3.
• cuadrilateroCuadro: Este método representa el caso 2 de las transformaciones proyectivas, donde al contrario del caso 1, se mapea un cuadrilátero irregular en un cuadrado unitario, recibe como parámetro una matriz bidimensional de 4x2 y regresa como resultado una matriz de transformación de 3x3, este método llama al método cuadroCuadrilatero y luego aplica la operación de matriz adjunta al resultado por medio del método matrizAdjunta.
• cuadrilateroCuadrilatero: Este método multiplica las 2 matrices de transformación obtenidas de los 2 casos anteriores por medio del método multiplicación y el resultado es la matriz de transformación u homografía final de 3x3, la cual es asignada a una variable que representa esta matriz.
• matrizAdjunta: Recibe como parámetro una matriz bidimensional de 3x3 y aplica la operación de matriz adjunta a esta. Este método ayuda al cálculo del caso 2 de transformaciones proyectivas, ya que la inversa de una matriz de homografía es una matriz de homografía.
• multiplicacion: Recibe como parámetro 2 matrices bidimensionales de 3x3 y las multiplica regresando una matriz bidimensional de 3x3. Este método ayuda al cálculo del caso 3, donde se tienen que multiplicar las matrices de transformación del plano origen y el plano destino para sacar la matriz de transformación que hace el mapeo entre estos 2 planos.
• transformacion: este método recibe como parámetro un punto 2D, la cual representa un punto (x,y) a ser transformado del un plano origen al plano destino y regresa un punto 2D, la cual representa el punto (x,y) transformado por medio de la matriz de transformación.

En el constructor se pasan como parámetros 2 matrices de 4x2, la primera representa los 4 puntos

(x,y) de las 4 esquinas del espacio de trabajo y la segunda los puntos (x,y) de las 4 esquinas de la pantalla de la computadora. Al llamar el método cuadrilateroCuadrilateo calcula la matriz de transformación para estos 2 planos, la cual es usada en el método transformacion para calcular el punto equivalente entre los 2 planos. Esta clase aunque fue escrita en Java, puede ser implementada en cualquier lenguaje de programación para así poder mapear un punto de un plano a otro y poder implementar un pizarrón interactivo en cualquier plataforma que se desee siempre y cuando se tengan las bibliotecas necesarias para conectar el Wiimote e interactuar con el stack del Bluetooth

 

4. Conclusiones

Después de analizar el software del pizarrón e investigar acerca de las homografías, como se describió en la sección 3, el algoritmo implementa los 3 casos vistos acerca de las transformaciones proyectivas, con el cual se pudo reproducir exitosamente la transformación de un punto detectado en un plano origen (la proyección usada como espacio de trabajo) a un plano destino (la pantalla de la computadora), implementado con el lenguaje de programación JAVA, y obteniendo un pizarrón interactivo básico, en cuanto a funcionalidad se refiere, pero con la misma capacidad que el del software WiimoteWhiteboard.

Al demostrar que el mapeo proyectivo funciona, se puede concluir que usando geometría proyectiva se puede mapear un plano arbitrario origen en uno destino, usando operaciones matriciales para convertir un punto ubicado en el espacio origen a su equivalente en el espacio destino.

Se comprueba que los 3 casos de la geometría proyectiva: de cuadro unitario a cuadrilátero, de cuadrilátero a cuadro unitario y de cuadrilátero a cuadrilátero, permiten resolver el sistema de 8 ecuaciones y obtener la matriz de transformación u homografía H mas rápido y fácil que al usar un algoritmo como DLT.

Finalmente, al implementar el código, se comprueba que siguiendo los 3 casos de las transformaciones proyectivas, se puede desarrollar un algoritmo genérico para poder crear un pizarrón interactivo infrarrojo funcional en cualquier lenguaje de programación.

 

Referencias

Jin, G. B. (2012) Smoothboard. Accesado desde http://www.smoothboard.net/wiimote/

Lee, J. C. (2012) Wii Remote Projects. Accesado desde http://johnnylee.net

Markowski, J. (2012) wiiBoardJ. Accesado desde http://wiiboardj.veuti.com

Peek, B. (2012) WiimoteLib - .NET Managed Library for the Nintendo Wii Remote. Accesado desde http://www.brianpeek.com/page/wiimotelib

Schmidt, U. (2012) Wiimote Whiteboard. Accesado desde http://www.uweschmidt.org/wiimote-whiteboard

 

Recebido / Recibido: 7/3/2015

Aceitação / Aceptación: 28/3/2015