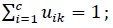ARTIGO

Análise de agrupamentos no estudo de caracteres agronômicos para a cultura do milho

Cluster Analysis in the study of agronomic traits for corn

Priscila Neves Faria^* e Douglas Silva Oliveira

Faculdade de Matemática/Núcleo de Estatística, Universidade Federal de Uberlândia, Uberlândia, Brasil

(*E-mail: priscilaneves@ufu.br)

---

RESUMO

Estudos a partir de dados genéticos são importantes para o conhecimento da variabilidade genética das populações, além de fornecer parâmetros para escolha de progenitores. Nos estudos para analisar o quão distante geneticamente um genótipo é de outro são utilizados métodos da estatística multivariada, permitindo unificar múltiplas informações de um conjunto de caracteres. Assim, o presente trabalho tem como objetivo utilizar dados de caracteres agronômicos de milho na aplicação do algoritmo de agrupamento fuzzy c-means, a fim de auxiliar na caracterização dos grupos obtidos, observando por meio do grau de relação do indivíduo com o grupo, qual tipo de indivíduo se agrega a um certo grupo. Foram identificados três agrupamentos com características específicas e os indivíduos do agrupamento 1 apresentaram desempenho agronômico superior quando comparados com os indivíduos dos outros agrupamentos.

Palavras-chave: linhagens, estatística multivariada, lógica difusa

---

ABSTRACT

Studies based on genetic data are important for the knowledge of the genetic variability of the populations, besides providing parameters for parent choice. In the studies to analyze how far genetically one genotype is from another are used multivariate statistical methods, allowing to unify multiple information of a set of characters. Thus, the present work aims used corn agronomic traits in the application of the fuzzy c-means clustering algorithm, in order to assist in the characterization of the groups obtained, observing through the degree of relationship of the individual with the group, which type of individual joins a certain group. Three clusters with specific characteristics were identified and the individuals of the first cluster presented superior agronomic performance when compared with the individuals of the other cluster.

Keywords: inbreeds, multivariate statistic, fuzzy logic

---

INTRODUÇÃO

A cultura do milho ocupou mais de 15,5 milhões de hectares na safra de 2013/2014 em território brasileiro, com produtividade média de 5,18 Mg/ha (ton/ha), sendo que, nos últimos anos, têm-se observado relevantes incrementos na produtividade de grãos dessa cultura. Isso se deve a mudanças tecnológicas recentes, tais como avanços no melhoramento genético, qualificação das adubações de base e de cobertura, modernização da mecanização agrícola, uso de irrigação e aprimoramento na gestão dos recursos agrícolas pela adoção da agricultura de precisão (Vian et al., 2016).

O potencial de produtividade de grãos de milho é determinado pela densidade de plantio, população final de plantas, número de espigas por planta, comprimento de espigas, número de fileiras de grãos por espiga, número de grãos por fileira, massa média do grão e pelo genótipo utilizado (Vian et al., 2016).

Estudos a partir de dados genéticos são importantes para o conhecimento da variabilidade genética das populações, além de fornecer parâmetros para escolha de progenitores. Para que estes estudos sejam realizados, é necessário muitas vezes o acesso aos dados de algum banco de germoplasma, acesso esse muitas vezes difícil de obter. Estima-se que 0,5% dos acessos de um banco devem ser requisitados por ano considerando que este seria o uso mínimo desejável (Brown, 1989).

Nos estudos para se analisar o quão distante geneticamente um genótipo é de outro são utilizados métodos da estatística multivariada, permitindo agrupar ou classificar objetos em categorias. Para realizar essa tarefa, pode ser empregado um mecanismo chamado análise de agrupamento.

A análise de grupos ou de agrupamento é uma técnica exploratória de análise multivariada que permite agrupar indivíduos ou variáveis em grupos homogêneos ou compactos relativamente a uma ou mais características comuns. Dessa forma, cada observação pertencente a um determinado agrupamento é similar a todas as outras pertencentes a esse agrupamento, e é diferente das observações pertencentes a outros agrupamentos (Mantovani, 2006).

Faria et al. (2013) aplicaram metodologias da estatística multivariada pensando na importância da espécie Capsicum chinense Jacq. (proveniente de banco de germoplasma) para agrobiodiversidade e melhor utilização do seu potencial, estudando a biometria de quarenta e nove acessos de pimenta.

Silva et al. (2016) avaliaram o crescimento e a produção de duas cultivares de milho verde submetidas a doses de Ribumin^® por meio de métodos da estatística multivariada como Análise de Agrupamentos e Análise de Componentes Principais.

No entanto, abordagens de agrupamento clássicos geram partições nas quais cada indivíduo pertence a um e somente um grupo, isto é, tem-se como resultado agrupamentos disjuntos. Mas na realidade o que acontece é a separação entre agrupamentos de maneira nebulosa, confusa, vindo daí o temo “fuzzy”. O conceito da lógica difusa (fuzzy logic) pode ser entendido como uma situação em que não basta responder simplesmente "sim" ou "não". Mesmo conhecendo as características necessárias sobre os indivíduos, dizer algo entre "sim" e "não", como "talvez" ou "quase", é mais adequado. Os conjuntos difusos oferecem a vantagem de expressar esta situação, de modo que se um indivíduo possui semelhanças com vários grupos, então o algoritmo poderá associar cada indivíduo parcialmente a todos grupos (Junior, 2006).

Assim, torna-se conveniente o uso de uma metodologia com a propriedade de descrever os valores de atributos, em vez de tentar fornecer uma representação numérica exata para os dados com valores incertos dos atributos. No tipo de abordagem não hierárquica, temos essa propriedade na metodologia difusa, mais flexível, na qual um objeto pode ser classificado em várias categorias, com diferentes graus de associação a cada uma delas.

No caso específico da análise de agrupamento difusa, diferentes métodos podem ser utilizados, por exemplo, o algoritmo fuzzy c-means, desenvolvido por Bezdek et al. (1984). Este algoritmo é um método de agrupamento que permite estabelecer, para um certo dado, um determinado grau de relação (também chamado de grau de pertinência) com cada um dos agrupamentos obtidos. O grau de relação entre uma amostra e um agrupamento é um valor que está no intervalo [0, 1]. Uma pertinência próxima a 1 significa que o indivíduo e o agrupamento em questão são similares. Caso contrário, se esse valor se aproxima de zero, indica dissimilaridade entre a amostra e o agrupamento analisado (Borges, 2010).

Uma relevante propriedade da modelagem difusa é a capacidade de codificar conhecimentos inexatos, de tal forma que se aproxime dos processos decisórios (Ruhoff et al., 2005). Os sistemas de inferência da lógica difusa proporcionam a apreensão do conhecimento próximo ao modelo “cognitivo” muito aplicado na análise de problemas de previsão e classificação. Logo, o processo de obtenção do conhecimento é simplificado, mais preciso e com menor probabilidade de erros.

As principais vantagens técnicas não-hierárquicas são que os resultados não são tão afetados por valores marginais e podem ser utilizados para grandes conjuntos de dados.

Considerando a importância da utilização de técnicas multivariadas em dados genéticos com estudos baseados em caracteres agronômicos, justifica-se a utilização do método fuzzy c-means em uma base de germoplasma, em que, no presente estudo foi aplicado à linhagens de milho.

MATERIAIS E MÉTODOS

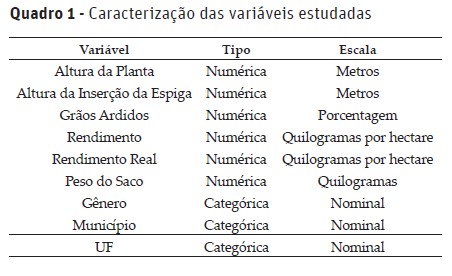
As linhagens avaliadas no estudo foram cedidas por uma multinacional sob termo de confidencialidade. A base original continha 1030 linhagens e 54 características avaliadas totalizando 298550 observações. No entanto, após eliminar do conjunto de dados os indivíduos com dados omissos para alguma característica, o conjunto de dados aqui estudado totalizou 13127 observações com 9 características, sendo que 6 dessas características foram utilizadas para a segmentação. Essas observações representam um acumulado no período entre 2012 e 2016 de várias localidades do Brasil. Para o estudo em questão foram consideradas nove características (Quadro 1) e destas, seis eram de interesse agronômico: Altura da Planta (m), Altura da Inserção da Espiga (m), Grãos Ardidos (%), Rendimento (Mg/ha), Rendimento Real (RE − AR − DE) e Peso do Saco (kg).

 

 

Apenas as variáveis de natureza numérica foram utilizadas para a segmentação dos indivíduos. Quanto às demais variáveis, essas foram utilizadas para caracterização e análises dos grupos já consolidados conforme será apresentado adiante.

Outro ponto a se destacar quanto às variáveis em estudo, é referente ao Rendimento Real, esse que por sua vez é calculado pela expressão RR = RE − AR – DE, em que RR é o Rendimento Real, RE é o Rendimento Total, AR é a quantidade (em kg/ha) de Grãos Ardidos e DE é a quantidade (em kg/ha) de Descarte.

Método fuzzy c-means

O algoritmo de agrupamento difuso mais popular é o fuzzy c-means. A ideia principal deste método é que não haja uma distância diferente de cada grupo até seus indivíduos. O método começa a partir de uma partição inicial e a cada passo modifica a distância do centro dos grupos a seus indivíduos, sendo este processo repetido até que o critério de convergência atinja um valor estacionário que representa um mínimo local, ou seja, não haja mais mudança na sua distância (Vargas, 2012). O problema mais importante no agrupamento difuso é a função de pertinência (grau de participação) uma vez que escolhas diferentes implicam decomposição de similaridades e de centroides de agrupamentos.

Supondo que se tem um conjunto de n indivíduos X = {x₁, … , x_n} em que cada indivíduo x_k ∈ ℝ_p, k = 1, … , n, e deseja-se organizá-los em c agrupamentos, C = {C₁, … ,C_c}. O algoritmo fuzzy c-means (Bezdek et al., 1984) é um método não hierárquico de agrupamento cujo objetivo é gerar uma partição difusa de um conjunto de indivíduos em c agrupamentos. Primeiramente o algoritmo define e minimiza uma função objetivo, cujo objetivo é maximizar a homogeneidade dentro de cada cluster e a heterogeneidade entre clusters. A função objetivo é definida como (Junior, 2006):

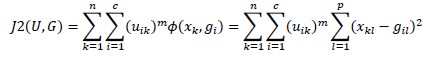
em que U ∈ M_{f cn} é uma matriz de pertinência {u_ik}, do indivíduo k ao agrupamento C_i; G é um vetor de protótipos dos agrupamentos ou centroides (g₁, … , g_K), g_i = (g_i1, … , g_ip); em que m ∈ ]1, + ∞[ é um parâmetro que controla a “nebulização” da pertinência dos indivíduos; e Ø(x_k,g_i) é o quadrado da distância L₂ Minkowsky, ou Euclidiana, a qual mede a dissimilaridade entre um indivíduo k e um protótipo de agrupamento i.

A distância Euclidiana utilizada no algoritmo é bastante sensível a ruídos, o que não faz diferença se o conjunto de dados não tem presença de ruídos ou outliers, mas, quando identifica-se a presença destes no conjunto de dados então o resultado final do algoritmo pode ser prejudicado (Döring et al., 2006).

O primeiro passo para execução do algoritmo é a partir de uma matriz de pertinência inicial, em seguida deve-se alternar um passo de representação e um passo de alocação até a convergência, isto é, quando o critério J2 (U,G) atinge um valor estacionário que corresponde a um mínimo, geralmente local (Junior, 2006). O sumário dos passos do algoritmo fuzzy c-means é dado pelo algoritmo a seguir.

Algoritmo Fuzzy c-means

O algoritmo Fuzzy c-means funciona por meio da realização dos seguintes passos:

1: Dados c, 2 ≤ c < n; 1 < m <∞>, T, como limite máximo de iterações e um escalar ε, de modo que ε > 0 mas ε seja pequeno;

2:Dado um método de iniciação, gere uma matriz de pertinência tal que a pertinência u_ik (i = 1, …, c e k = 1, …, n) e do indivíduo k ao agrupamento C_i seja tal que u_ik > 0 e

3: para t = 1 até T fazer

4:  A pertinência u_ik do indivíduo k ao agrupamento C_i está fixa;

5:Calcule os protótipos g_i do agrupamento C_i usando a equação 2.24 mencionada em Junior (2006);

6:  {Os protótipos g_i dos agrupamento C_i estão fixos}

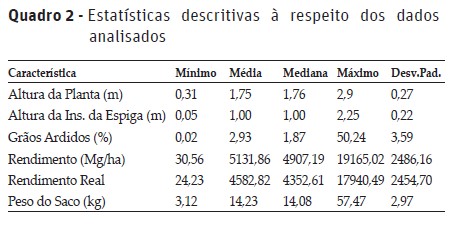
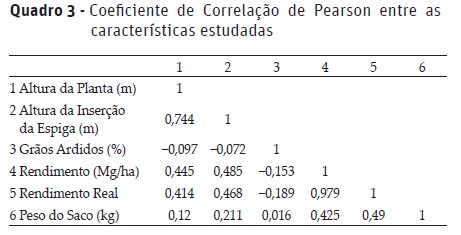
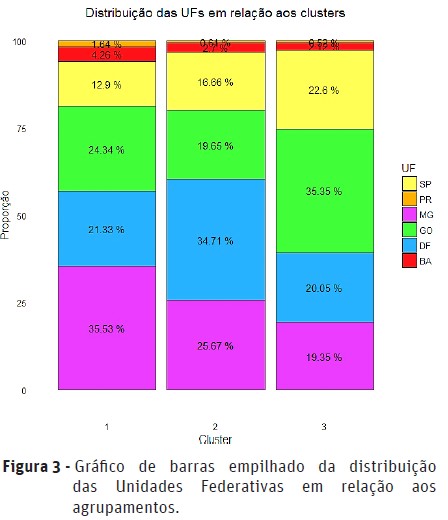
Atualize o grau de pertinência u_ik do indivíduo k ao agrupamento C_i para i = 1, …, c usando a equação 2.25 mencionada em Junior (2006);

7: Critério de parada:

8: se |J2^(t+1)-J2^t| , pare. Caso contrário, defina J2^t = J2^(t+1) e retorna ao passo 5.

10: fim se

11: fim para

RESULTADOS E DISCUSSÃO

Inicialmente foi realizada uma análise descritiva para evidenciar a variabilidade dos dados e a descrição das características dos indivíduos segue abaixo no Quadro 2.

Além das estatísticas descritivas obtidas no Quadro 2, foi verificado que aproximadamente 97% dos indivíduos analisados estão sendo utilizados no programa de melhoramento como fêmeas (F).

 

 

As características Altura da Planta (m), Altura da Inserção da Espiga (m), Grãos Ardidos (%), Rendimento (Mg/ha), Rendimento Real (RE − AR − DE) e Peso do Saco (kg) apresentam escalas distintas. Para evitar o efeito de determinadas escalas, os dados foram padronizados pela padronização Gaussiana.

O Quadro 3 apresenta os valores referente ao cálculo do Coeficiente de Correlação de Pearson, verificando a existência de associação linear entre as características estudadas.

 

 

As características que apresentaram correlação linear forte entre si foram o Rendimento Real e o Rendimento, além da Altura da Planta e a Altura de Inserção da Espiga.

Com o auxílio do pacote fclust, foi obtida a formação de três agrupamentos pelo Método fuzzy c-means de maneira que não houvesse influência de determinada característica devido à escala. A quantidade de agrupamentos foi determinada através de gerações sucessivas e comparações.  Foram realizados experimentos considerando 2, 3, 4 e 5 agrupamentos, sendo que o experimento 2 agrupamentos não ajudou a diferenciar os indivíduos, enquanto que os experimentos de tamanho 4 e 5 não apresentaram grandes diferenças do experimento de tamanho 3. Por esse motivo, optou-se pelo experimento com divisão entre três agrupamentos. A distribuição dos indivíduos em relação aos três agrupamentos foi a seguinte: Agrupamento 1 com 3853 indivíduos, Agrupamento 2 com 4881 e o Agrupamento 3 com 4393 indivíduos.

Neste tipo de agrupamento os indivíduos não pertencem a um único agrupamento mas aos c agrupamentos determinados pelo pesquisador, porém, com um grau de pertinência maior em um dos agrupamentos. Sendo assim, os indivíduos que foram agrupados do agrupamento 1 apresentaram maior grau de pertinência nesse agrupamento em relação aos demais agrupamentos. De maneira análoga é possível explicar o agrupamento dos demais indivíduos nos agrupamentos 2 e 3 (Quadro 4).

Na Figura 1, com a análise visual do comportamento das características dentro de cada um dos agrupamentos, foi verificado que os indivíduos com maior grau de pertinência no agrupamento 1 apresentaram características como a Altura da Planta (m), o Rendimento (Mg/ha), o Rendimento Real (RE − AR − DE) e o Peso do Saco (kg) superiores aos indivíduos dos demais agrupamentos. Quanto às características Altura da Planta (m) e Altura da Inserção da Espiga (m), essas apresentaram valores menores para os indivíduos do agrupamento 3.

Além disso, os indivíduos com maior grau de pertinência no agrupamento 3 apresentaram um comportamento superior quanto a quantidade de Grãos Ardidos (%) em relação aos indivíduos dos demais agrupamentos. Por fim, os indivíduos que apresentaram maior grau de pertinência no agrupamento 2, destacaram-se por serem indivíduos que apresentam características intermediárias em relação aos indivíduos dos agrupamentos 1 e 3 (Figura 1).

Foi observado que os indivíduos que apresentaram maior grau de pertinência para o agrupamento 1 também apresentaram o menor grau de pertinência para o agrupamento 3 e vice-versa (Figura 2). Desta forma, pelos resultados obtidos, as linhagens com maior grau de relação com o grupo 1 terão menor grau de relação com o grupo 3. Isto  também foi confirmado pela Tabela 4, uma vez que o grupo 1 possui linhagens com maiores valores registrados em quatro dos seis caracteres agronômicos em estudo, já o grupo 3 possui linhagens com os menores registros quando comparados com o grupo 1.  Quanto aos indivíduos que apresentaram maior grau de pertinência para o agrupamento 2, estes são intermediadores entre os demais agrupamentos (Figura 2).

Os indivíduos do agrupamento 1 são predominantes no estado de MG (Figura 3), enquanto que os indivíduos do agrupamento 2 e 3, apresentam predominância no DF e no estado de GO, respectivamente.

 

 

Aparentemente, nenhuma região se destacou quanto ao agrupamento (Figura 3). Apesar de haver certa predominância de determinadas Unidades Federativas, não foi possível garantir que uma suposição a respeito da influência climática e geológica das regiões quanto à produção dessas culturas estudadas.

CONCLUSÃO

Nesse estudo, em específico, foi possível avaliar o comportamento de linhagens de milho, proveniente de um banco de germoplasma cedido por empresa Multinacional sob termo de confidencialidade, por meio do método de segmentação fuzzy c-means. Dessa maneira, foram identificados três agrupamentos com características específicas.

Em destaque temos os indivíduos do agrupamento 1 que apresentaram um comportamento superior aos indivíduos dos demais agrupamentos em relação ao Rendimento e ao Rendimento Real.

 

Referências Bibliográficas

Bezdek, J.C.; Ehrlich, R. & Full, W. (1984) - FCM: The fuzzy c-means clustering algorithm. Computers & Geosciences, vol. 10, n. 2-3, p. 191–203. https://doi.org/10.1016/0098-3004(84)90020-7

Borges, V.R.P. (2010) - Comparação entre as Técnicas de Agrupamento K-Means e Fuzzy C-Means para Segmentação de Imagens Coloridas. XII Encontro Anual de Computação (EnAComp).         [ Links ]

Brown, A.H.D. (1989) - The case for core collections. In: Brown, A.H.D.; Frankel, O.H.; Marshall, D.R. & Williams, J.T. (Eds.) - The use of plant genetic resources. New York: Cambridge University Press, p.136-156.         [ Links ]

Döring, C.; Lesot, M.J. & Kruse, R. (2006) - Data Analysis with Fuzzy Clustering Methods. Computational Statistics & Data Analysis, vol. 51, n. 1, p. 192-214. https://doi.org/10.1016/j.csda.2006.04.030        [ Links ]

Faria, P.N.; Laia, G.A.; Cardoso, K.A.; Finger, F.L. & Cecon, P.R. (2013) - Estudo da variabilidade genética de amostras de pimenta (Capsicum chinense Jacq.) existentes num banco de germoplasma: um caso de estudo. Revista de Ciências Agrárias, vol. 36, n. 1, p. 17-22. https://doi.org/10.19084/rca.16276        [ Links ]

Junior, N.L.C. (2006) - Clusterização baseada em algoritmos fuzzy. Dissertação de Mestrado - Ciência da Computação, Universidade Federal de Pernambuco.         [ Links ]

Mantovani, L.S.D. (2006) - O processo de escolha de serviço de telefonia celular dos jovens em Curitiba. Dissertação de Mestrado. UFPR.         [ Links ]

Ruhoff, A.L.; Souza, B.S.P.; Giotto, E. & Pereira, R.S. (2005) - Lógica Fuzzy e Zoneamento Ambiental da Bacia do Arroio Grande. Anais do XII Simpósio Brasileiro de Sensoriamento Remoto, Goiânia-Brasil, INPE, p.2355-2362.         [ Links ]

Silva, R. de A.; Souza, U.O.; Santos, L.G. dos; Melo, N.C. & Vasconcelos, R.C. de (2016) - Características agronômicas de cultivares de milho verde submetidas a doses de Ribumin. Revista de Ciências Agrárias, vol. 39, n. 3, p. 395-403. https://doi.org/10.19084/RCA15126        [ Links ]

Vargas, R.R. de (2012) - Uma nova forma de calcular os centros dos clusters em algoritmos de agrupamento tipo Fuzzy C-Means. Tese (Doutorado) — Universidade Federal do Rio Grande do Norte – Centro de Tecnologia.

Vian, A.L.; Santi, A.L.; Amado, T.J.C.; Cherubin, M.R.; Simon, D.H.; Damian, J.D. & Bredemeier, C. (2016) - Variabilidade espacial da produtividade de milho irrigado e sua correlação com variáveis explicativas de planta. Ciência Rural, vol. 46, n. 3, p. 464–471. http://dx.doi.org/10.1590/0103-8478cr20150539

 

Recebido/received: 2019.01.22

Aceite/accepted: 2019.06.11