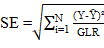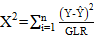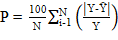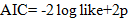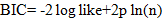INTRODUÇÃO
A semente consiste em um insumo básico para a produção de alimentos (Jilito et al., 2020), pois nela está contida a informação para o desenvolvimento de uma futura planta (Chable et al., 2020). Para que a semente conserve as suas características germinativas é necessário um adequado armazenamento, pois, após a colheita, a semente continua num processo contínuo de respiração e deterioração natural (Marcos Filho, 2015).
Neste contexto, a secagem consiste num processo de extrema importância na tecnologia de alimentos, pois permite o manuseio de produtos de alta qualidade, preservando suas propriedades físicas e químicas e reduzindo o teor de água a valores adequados para armazenamento (Jorge et al., 2021). A secagem pode ser estimada por meio de curvas ajustadas a dados experimentais por modelos de regressão não-lineares frequentemente usados para estimar esse processo (Sousa et al., 2017; Souza et al., 2019).
A secagem e o armazenamento da semente devem garantir a qualidade da semente, pois, a utilização de sementes de alta qualidade é um fator fundamental para a colheita promissora (Ferreira et al., 2017). Em função disso, é de suma importância a realização de testes em laboratórios e em campo para a avaliação do vigor de sementes (Rocha et al., 2015). Esses testes podem ser o teste de germinação de sementes (Marcos Filho, 2015); o índice de velocidade de emergência (Krzyzanowski et al., 1999) e o de condutividade elétrica (Lemes et al., 2015).
Diversos trabalhos foram realizados com o objetivo de estudar o processo de secagem em milho, seja semente ou grão. Souza e Ruffato (2021) estudaram o processo de secagem natural e seu efeito na qualidade de grãos de milho. Os autores verificaram que a redução do teor de água promoveu aumento da massa específica aparente e unitária dos grãos, enquanto que a qualidade fisiológica, não foi influenciada. Já Coradi et al. (2020), estudaram a influências da temperatura de secagem e das condições de armazenamento na preservação da qualidade do milho pós-colheita. De forma geral, os autores observaram que o aumento da temperatura do ar de secagem acelerou a redução do teor de água do grão, no entanto, aumentou a deterioração. Em relação ao armazenamento, foi verificado que a armazenagem hermética e arejada manteve a qualidade química dos grãos de milho.
Diante da importância do armazenamento adequado das sementes de milho, objetivou-se com o presente trabalho determinar e modelar a cinética de secagem de sementes de milho orgânico em diferentes temperaturas bem como avaliar a qualidade fisiológica das mesmas após a secagem.
MATERIAL E MÉTODOS
O estudo foi conduzido no Laboratório de Análise de Sementes (LAS) do Instituto Federal Goiano - Campus Ceres. As sementes de milho orgânico cultivar ‘BRS Caimbé’ foram adquiridas à Empresa Grãos Orgânicos Ltda, localizada em Minas Gerais, no município de Fortuna, Brasil. As sementes foram adquiridas com teor de água inicial de aproximadamente 10,64v% base úmida (b.u).
Para a realização da secagem foi necessário realizar o processo de umedecimento das sementes de milho orgânico, com o intuito de elevar o ter de água de 10,64 para 20 % (b.u). Dessa forma, adicionou-se água destilada às amostras e, posteriormente, estas foram acondicionadas em geladeira por 4 dias. Após o processo de umedecimento, o teor de água das sementes em base seca (b.s.) foi determinado utilizando o método de estufa ventilada a 105 ± 1 °C durante 24-h, em triplicado (Brasil, 2009).
Em seguida, as sementes foram secas em estufa de circulação forçada a 30, 40, 50 e 60 °C. As sementes foram secas até atingirem o teor de água adequado (11% kg-1 peso seco) para armazenamento (Silva et al., 2008). Para cada temperatura, quatro repetições de aproximadamente 250 g de sementes foram dispostas em bandejas de metal em uma única camada. O teor de água das sementes foi monitorado por gravimetria, por meio da pesagem das sementes periodicamente em balança analítica (resolução de 0,01 g).
Ao final do processo de secagem, foi determinado o teor de água em base seca, e posteriormente, realizado o cálculo da razão do teor de água (RX) durante os processos de secagem pela equação 1.
Em que: X - teor de água do produto, decimal b.s.; Xi - teor de água inicial do produto, decimal b.s.; Xe - teor de água de equilíbrio do produto, decimal b.s.
O teor de umidade de equilíbrio das sementes sob cada condição de secagem foi calculado usando o modelo de Oswin Modificado, cujos valores foram 11,68, 11,16, 10,65 e 10,13 % (b.s.), respectivamente, para temperaturas de 30, 40, 50 e 60 ° C. Já a umidade relativa do ar de secagem foi de 46% para todas as condições de secagem. Este modelo foi recomendado por Smaniotto et al. (2012) para estimar a dessorção isotermas de sementes de milho cultivar ‘AG 7088’.
A partir do RX de cada condição de secagem, realizou-se o ajuste de diferentes modelos matemáticos não-lineares, frequentemente utilizados para representar a cinética de secagem de produtos agrícolas, conforme o Quadro 1 (Alves et al., 2013; Moscon et al., 2017; Smaniotto et al., 2017).
Quadro 1 Modelos matemáticos utilizados para predizer o fenómeno de secagem
| Designação do modelo | Modelo | Nº |
| Aproximação por Difusão | RX=a.exp(-k.t)+(1-a)exp(-k.b.t) | 2 |
| Dois termos | RX=a.exp(-k1.t)+b.exp(-k2.t) | 3 |
| Henderson e Pabis | RX=a.exp(-k.t) | 4 |
| Henderson e Pabis Modificado | RX=a.exp(-k.t)+b.exp(-k1.t)+c.exp(-k2.t) | 5 |
| Exponencial de dois termos | RX=a.exp(-k.t)+(1-a)exp(-k.a.t) | 6 |
| Logarítmico | RX=a.exp(-k.t)+c | 7 |
| Newton | RX=exp(-k.t) | 8 |
| Midilli | RX=a.exp(-k.tn)+b.t | 9 |
| Midilli modificado | RX=exp(-k.tn )+a.t | 10 |
| Page modificado | RX=exp(-(k.tn)) | 11 |
| Page | RX=exp(-k.tn) | 12 |
Em que: RX - razão do teor de água do produto (adimensional); t - período de secagem, horas; k, k1, k2- coeficiente de secagem; a, b, c e n - constantes empíricas dos modelos.
Na seleção dos melhores modelos para representar a cinética de secagem de sementes de milho orgânico, foram considerados a significância dos coeficientes de regressão pelo teste t a p ≤ 0,05, a magnitude do coeficiente de determinação (R2), o erro médio relativo (P), o teste de qui-quadrado (χ2) e o desvio padrão de estimativa (SE).
Para a recomendação do modelo matemático de cinética de secagem, foi verificado o R2 mais próximo à magnitude, valores de P abaixo de 10% e os valores de SE e χ2 mais próximos de zero. Os valores do desvio padrão da estimativa (SE), teste de qui-quadrado (χ2) e o erro médio relativo (P) foram calculados pelas equações 13, 15 e 15.
em que:
N - número de observações experimentais;
Y - razão de teor de água experimental;
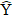 - razão de umidade predito; e,
- razão de umidade predito; e,
GLR - grau de liberdade do resíduo.
Para escolher um único modelo de regressão que melhor descreve o processo de secagem das sementes de milho orgânico, critérios adicionais foram usados. Para os modelos que obtiveram melhores ajustes de acordo com os critérios listados anteriormente, o Critério de Informação de Akaike (AIC) e o Critério de Informação Bayesiano de Schwarz (BIC) foram calculados usando as equações 16 e 17:
Onde:
p - número de parâmetros do modelo;
n - número total de observações; e,
loglike - valor do logaritmo da função de verossimilhança considerando as estimativas dos parâmetros.
Após a secagem em cada temperatura, a qualidade fisiológica das sementes foi avaliada pelo teste de germinação, primeira contagem de germinação (Brasil, 2009), condutividade elétrica (Vieira & Krzyzanowski, 1999), emergência (Nakagawa, 1994, 1999) e índice de velocidade de emergência de plântulas (IVE) (Maguire, 1962). Todos os testes foram realizados com quatro repetições de 50 sementes para cada tratamento.
O delineamento utilizado foi o inteiramente casualizado, sendo constituído de quatro temperaturas de secagem (30, 40, 50 e 60 ° C). Os testes de qualidade fisiológica foram submetidos a análise de regressão a 5% de probabilidade.
RESULTADOS E DISCUSSÃO
O teor de água das sementes de milho orgânico após o umedecimento foi de aproximadamente 30 % b.s. (Figura 1). Os tempos de secagem necessários para reduzir o teor de água das sementes para 11% foram 84,3, 20,0, 14,3 e 8,6 horas, respectivamente, para as temperaturas de 30, 40, 50 e 60 °C. A redução no tempo de secagem pode ser explicada pela maior taxa de retirada de água observada em temperaturas mais elevadas (Silva et al., 2018) (Figura 1).
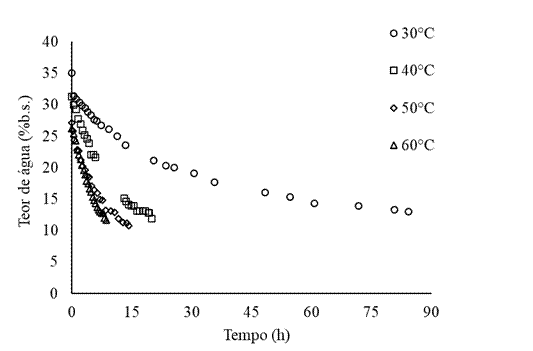
Figura 1 Teor de água durante a secagem das sementes de milho orgânico cultivar ‘BRS Caimbé’ em diferentes temperaturas.
No trabalho de Coradi et al. (2016), referente a secagem de sementes de milho em secador de fluxo contínuo, foi observado que a elevação da temperatura do ar de secagem promoveu o aumento da remoção de água da semente e, consequentemente, a diminuição do tempo de secagem. Já Paraginski et al. (2015), observaram que durante o armazenamento e a secagem de sementes de milho em ambiente semi- hermético, ocorreu a diminuição constante do teor de água a partir da temperatura de 35 ºC.
No Quadro 2 são apresentados os valores do coeficiente de determinação, erro médio estimado, erro médio relativo e teste de qui-quadrado dos diferentes modelos matemáticos ajustados aos dados experimentais da secagem das sementes de milho orgânico para as diferentes temperaturas de secagem. Nota-se que todos os modelos apresentaram coeficientes de determinação superiores a 96%. No entanto, segundo Corrêa et al. (2015), o uso isolado deste parâmetro não é suficiente para caracterizar ajuste adequado de modelos não lineares, sendo assim necessário considerar outros parâmetros estatísticos (Zeymer et al., 2017).
Quadro 2 Graus de ajuste dos modelos para a secagem das sementes de milho orgânico cultivar ‘BRS Caimbé’ em quatro temperaturas de secagem
| Modelo matemático | Temperatura | (R2) | SE (Decimal) | P (%) | χ² (Decimal) |
| (°C) | |||||
| Aproximação por difusão | 30 | 99,81 | 0,0513 | 4,0357 | 0,0026 |
| 40 | 99,77 | 0,0559 | 3,9689 | 0,0031 | |
| 50 | 99,41 | 0,0853 | 8,7353 | 0,0073 | |
| 60 | 99,63 | 0,0732 | 4,9396 | 0,0054 | |
| Dois termos | 30 | 99,80 | 0,0556 | 4,3075 | 0,0031 |
| 40 | 99,46 | 0,0913 | 7,1843 | 0,0083 | |
| 50 | 99,07 | 0,1180 | 40,1525 | 0,0139 | |
| 60 | 99,85 | 0,0444 | 3,4908 | 0,0020 | |
| Exponencial de dois termos | 30 | 96,61 | 0,2117 | 13,1081 | 0,0448 |
| 40 | 99,36 | 0,0922 | 8,6088 | 0,0085 | |
| 50 | 99,08 | 0,1075 | 40,6551 | 0,0115 | |
| 60 | 97,33 | 0,2069 | 14,9276 | 0,0428 | |
| Henderson e Pabis | 30 | 98,66 | 0,1052 | 7,0538 | 0,0111 |
| 40 | 99,46 | 0,0854 | 7,1843 | 0,0073 | |
| 50 | 99,07 | 0,1180 | 40,1530 | 0,0139 | |
| 60 | 98,40 | 0,1505 | 11,1824 | 0,0226 | |
| Logarítmo | 30 | 98,91 | 0,0968 | 5,8765 | 0,0094 |
| 40 | 99,82 | 0,0455 | 3,0115 | 0,0021 | |
| 50 | 99,51 | 0,0522 | 10,9214 | 0,0027 | |
| 60 | 99,73 | 0,0610 | 4,1481 | 0,0037 | |
| Newton | 30 | 92,46 | 0,3471 | 22,7622 | 0,1205 |
| 40 | 99,36 | 0,0894 | 8,6086 | 0,0080 | |
| 50 | 99,04 | 0,1118 | 38,8209 | 0,0125 | |
| 60 | 97,33 | 0,1973 | 14,9273 | 0,0389 | |
| Midilli | 30 | 99,55 | 0,0716 | 3,9389 | 0,0051 |
| 40 | 99,82 | 0,0451 | 2,8382 | 0,0020 | |
| 50 | 99,60 | 0,0708 | 7,7255 | 0,0050 | |
| 60 | 99,89 | 0,0362 | 2,6367 | 0,0013 | |
| Midilli Modificado | 30 | 99,42 | 0,0081 | 5,5582 | 0,0006 |
| 40 | 99,82 | 0,0432 | 2,8220 | 0,0019 | |
| 50 | 99,59 | 0,0663 | 8,1946 | 0,0044 | |
| 60 | 99,89 | 0,0350 | 2,6288 | 0,0012 | |
| Page Modificado | 30 | 98,98 | 0,1059 | 8,4632 | 0,0112 |
| 40 | 99,73 | 0,0584 | 4,2157 | 0,0584 | |
| 50 | 99,06 | 0,1180 | 36,2236 | 0,0139 | |
| 60 | 99,86 | 0,0412 | 3,2963 | 0,0017 | |
| Page | 30 | 98,98 | 0,1059 | 8,4632 | 0,0112 |
| 40 | 99,73 | 0,0603 | 4,2157 | 0,0584 | |
| 50 | 99,06 | 0,1150 | 36,2236 | 0,0132 | |
| 60 | 99,86 | 0,0412 | 3,2963 | 0,0017 |
Para que um modelo represente satisfatoriamente qualquer fenômeno, ele deve apresentar erro médio relativo (P) menor que 10% (Mohapatra e Rao, 2005); erro médio estimado (SE) e teste de qui-quadrado (χ²) mais próximo de zero (Günhan et al., 2005; Siqueira et al., 2012). Dessa forma, em relação ao SE e χ², verifica-se que os modelos Midili Modificado (SE = ≤ 0,0663 e χ² = ≤ 0,0044) e Logarítmo (SE = ≤ 0,0968 e χ² = ≤ 0,0094) foram os que apresentaram os melhores resultados nas condições estudadas. Já em relação ao P, nota-se que somente o modelo Midili Modificado apresentou valores inferiores a 10% para todas as temperaturas de secagem (Quadro 2).
O Critério de Informação Bayesiano de Schwarz (BIC) e o Critério de Informação de Akaik (AIC) também foram utilizados como parâmetros complementares para selecionar o melhor modelo entre os que se destacaram em relação aos parâmetros estatísticos calculados anteriormente (Midili Modificado e Logarítmo) (Quadro 3). De acordo com os resultados apresentados por Ferreira Junior et al. (2018), valores menores para esses critérios indicam melhor ajuste do modelo aos dados do fenomeno.
Quadro 3 Critério de Informação de Akaike (AIC) e Critério de Informação Bayesiano de Schwartz (BIC) dos modelos ajustados para curvas de secagem das sementes de milho orgânico cultivar ‘BRS Caimbé’ em diferentes temperaturas
| Modelo matemático | Temperatura | AIC | BIC |
| (°C) | |||
| Midilli modificado | 30 | -113,7037 | -108,8282 |
| 40 | -98,1644 | -94,6029 | |
| 50 | -79,7619 | -76,2004 | |
| 60 | -140,3507 | -135,8087 | |
| Logarítimico | 30 | -97,9363 | -93,0608 |
| 40 | -98,0096 | -94,4481 | |
| 50 | -77,7913 | -74,2298 | |
| 60 | -122,6163 | -118,0743 |
Verifica-se no Quadro 3 que o modelo Midilli Modificado apresentou valores mais baixos de AIC e BIC nas condições de secagem estudada e, portanto, este foi o modelo escolhido para representar a cinética de secagem das sementes de milho orgânico. Quequeto et al. (2019) que trabalharam com a secagem de sementes de Morinda citrifolia L., também utilizaram os critérios AIC e BIC para selecionar o modelo mais adequado.
No Quadro 4 encontram-se os valores dos coeficientes do modelo Midilli Modificado para as diferentes temperaturas de secagem. Constata-se que os coeficientes “k”, “n” e “a” não apresentaram tendência de comportamento em relação ao aumento da temperatura. Todos os coeficientes foram significativos a 5 % de probabilidade pelo teste t. De acordo com Babalis e Belessiotis (2004), o coeficiente “k”, que representa as condições externas de secagem, pode ser utilizado como uma aproximação para caracterizar o efeito da temperatura e está relacionado com a difusividade efetiva no processo de secagem no período decrescente e à difusão liquida que controla o processo.
Quadro 4 Valores dos parâmetros dos modelos ajustados para sementes de milho orgânico cultivar ‘BRS Caimbé’ em diferentes temperaturas de secagem 30, 40, 50 e 60°C
| Modelo | Parâmetros | Temperaturas | |||
| 30°C | 40°C | 50°C | 60°C | ||
| Midilli Modificado | k | 0,1430** | 0,1064** | 0,2069** | 0,1291** |
| n | 0,5739** | 0,9743** | 0,8496** | 1,2548** | |
| a | -0,001** | -0,0059** | -0,0090** | -0,0046** | |
**Significativo a 95% de probabilidade pelo teste t.
Na Figura 2 apresentam-se as curvas de secagem obtidas a partir do modelo Midilli Modificado para as diferentes condições de secagem estudadas. Constata-se que o modelo Midilli Modificado foi capaz de simular as diferentes temperaturas de secagem de forma satisfatória, adequando-se bem aos dados experimentais. De acordo com Goneli et al. (2014), o melhor ajuste do modelo de Midilli aos dados experimentais de secagem está ligado, provavelmente, à rápida perda de água nos estádios iniciais do processo gerando uma curva de secagem de maior declive e bem caracterizada matematicamente, por este modelo. Este modelo foi recomendado por Corrêa et al. (2010) para predizer a secagem de frutos de Coffea arabica L.
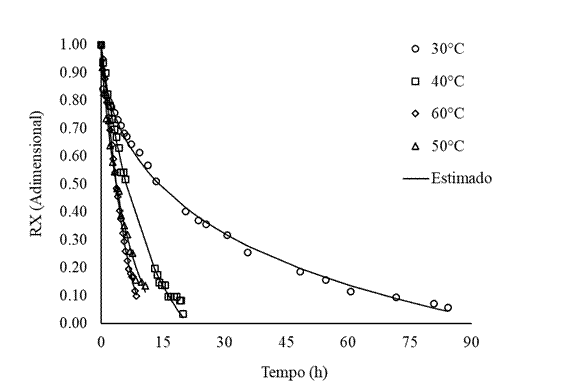
Figura 2 Valores da razão de umidade obtidos experimentalmente e estimados pelo modelo Midilli Modificado para a secagem de sementes de milho orgânico cultivar ‘BRS Caimbé’ durante o período de secagem em diferentes temperaturas
Em relação à qualidade fisiológica das sementes, verificou-se que a germinação decresceu e, portanto, foi influenciada pelas temperaturas de secagem, onde o aumento da temperatura promoveu um decréscimo nessa variável (Figura 3). Os resultados corroboram com os obtidos por Akowuah et al. (2018), onde a secagem de sementes de milho com temperaturas variando de 52,8 ± 5,4 a 44,4 ± 4,6 ºC, resultaram na redução da germinação das sementes. Já Costa et al. (2012), que estudaram a secagem de frutos de crambe (Crambe abyssinica Hochst) em diferentes temperaturas, observaram maiores valores de germinação em sementes submetidas a secagem na temperatura de 30 ºC, resultado semelhante ao encontrado no presente trabalho, onde a germinação das sementes foi superior a 90 % nesta temperatura.
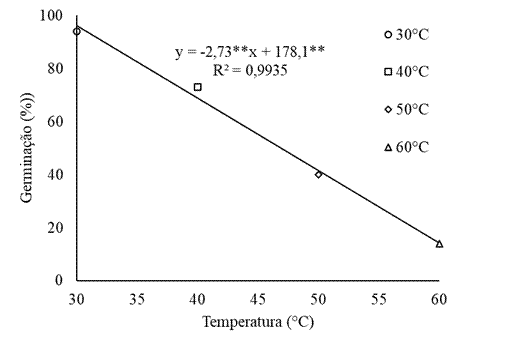
Figura 3 Germinação de sementes de milho orgânico cultivar ‘BRS Caimbé’ em diferentes temperaturas de secagem (** significativo a 5 % de probabilidade).
Menores valores de germinação, principalmente nas temperaturas de 50 e 60 ºC (40 e 14 %, respectivamente), pode estar relacionada às temperaturas elevadas durante a secagem (Akowuah et al., 2018). Segundo Paraginski et al. (2015), a diminuição da germinação das sementes está relacionada com as modificações que acontecem nas membranas citoplasmáticas devido ao aumento de temperatura.
Na Figura 4 estão ilustrados os valores da porcentagem de emergência para as sementes de milho orgânico, submetidas à secagem em diferentes temperaturas. Constata-se o decréscimo linear na porcentagem de emergência com o aumento da temperatura, demonstrando que temperaturas elevadas são prejudiciais às sementes cujo comportamento foi similar ao da germinação, que também apresentou decréscimo gradativo assim que a temperatura se elevou, evidenciando a diminuição do vigor das sementes. Já na Figura 5, estão apresentados os valores do índice de velocidade de emergência (IVE). Verifica-se que o comportamento do IVE foi linearmente reduzido com o aumento da temperatura evidenciando, assim, o a diminuição da qualidade fisiológica e do vigor das sementes.
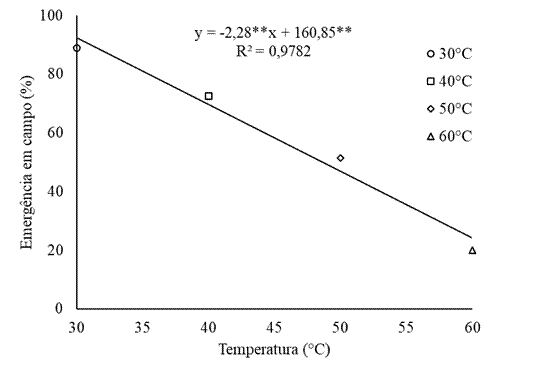
Figura 4 Emergência de sementes de milho orgânico cultivar ‘BRS Caimbé’ em diferentes temperaturas do ar de secagem (** significativo a 5 % de probabilidade).´
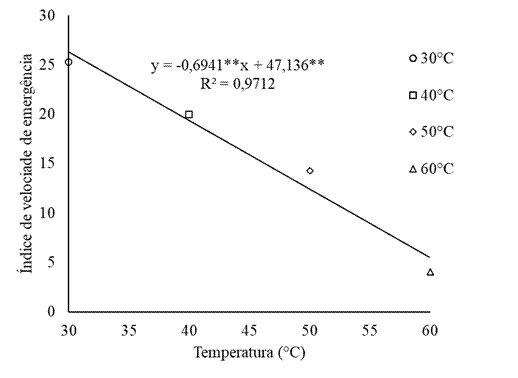
Figura 5 Índice de Velocidade de emergência de sementes de milho orgânico cultivar ‘BRS Caimbé’ em diferentes temperaturas de secagem. ** significativo a 5 % de probabilidade.
Ullmann et al. (2015), que estudaram o processo de secagem de sementes de sorgo sacarino, observaram a diminuição do índice de velocidade de emergência devido ao aumento da temperatura, resultado semelhante ao obtido no presente trabalho. Já Oliveira et al. (2016), que trabalharam com secagem de sementes de milho da cultivar ‘AG 7088’, verificaram aumento da velocidade de emergência entre as temperaturas de 40º e 70 ºC, e somente em temperaturas maiores, se obteve uma queda no índice. Salienta-se que o aumento da temperatura promove danos na estrutura física da semente, comprometendo sua fisiologia e, consequentemente, o seu desenvolvimento, como a velocidade de emergência das sementes.
Na Figura 6 observam-se os valores de condutividade elétrica em função das diferentes temperaturas de secagem. Salienta-se que não houve significância no ajuste de regressão para esta variável. Entretanto, de forma geral, verifica-se que o incremento da temperatura promoveu o aumento desta variável. Valores mais elevados de condutividade elétrica estão ligados a uma maior libertação de exsudatos para o meio ambiente através da membrana citoplasmática, indicando maior rompimento dessas (Carvalho et al., 2016). Resultados semelhantes foram descritos para sementes de Vigna angularis Willd (Resende et al., 2012; Almeida et al., 2013) e sementes de milho (Oliveira et al., 2016).
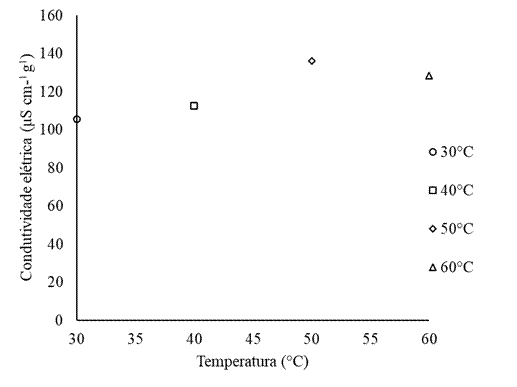
Figura 6 Condutividade elétrica de sementes de milho orgânico da cultivar ‘BRS Caimbé’ em diferentes temperaturas de secagem. **ns- não-significativo a 5 % de probabilidade.
Oliveira et al. (2016) afirmam que o incremento de temperatura de secagem em sementes de milho contribui para o aumento de danos nas membranas celulares enquanto que Paraginski et al. (2015) referem que temperaturas mais baixas diminuem as modificações em sementes, favorecendo a longevidade das mesmas. Neste contexto, verifica-se que a realização da secagem de sementes de milho a 30 °C foi a mais indicada para manutenção da qualidade fisiológica.
CONCLUSÕES
O modelo que melhor representou a cinética de secagem de sementes de milho orgânico foi o de Midilli modificado nas temperaturas de 30, 40, 50 e 60 °C.
A temperatura de secagem que proporcionou melhores resultados para a qualidade fisiológica de sementes de milho orgânico ‘BRS Caimbé’ foi a de 30 ºC.
O aumento da temperatura promoveu a redução no teor de água das sementes de milho orgânico ‘BRS Caimbé’ e a diminuição da germinação, nas condições estudadas.