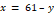O que seria dos professores, dos experts e dos pesquisadores se lhes pedissem que dissessem o que aprenderam, o que viveram, o que pensaram, e não o que lhes foi ensinado? Jorge Larrosa, 2014, p. 82
Introdução
Dentre todas as formas possíveis de comunicação em sala de aula, na disciplina de matemática, a escrita parece ser a forma mais comum, se constituindo, quase sempre, como principal recurso que os professores utilizam para que os alunos expressem o que sabem. Ao lidar com uma situação matemática, o registro escrito não é apenas importante, mas necessário, dependendo da complexidade da situação, das variáveis envolvidas, dos objetivos traçados pelo professor. Os registros escritos são necessários, como meio de organização e manutenção das ideias desenvolvidas, e, importantes, para veicular e comunicar uma solução, uma forma de pensamento, uma maneira de lidar.
Pesquisas geradas pelo GEPEMA - Grupo de Estudos e Pesquisa em Educação Matemática e Avaliação4 - tiveram como objeto de estudo a análise da produção escrita e a avaliação como prática de investigação, e, como meta, conhecer as formas pelas quais alunos e professores lidavam com as tarefas matemáticas propostas. A análise da produção escrita é apreciada como um dos recursos para que a avaliação escolar seja entendida como uma prática de investigação. Nesse sentido, a análise da produção escrita é uma prática que pode ser considerada tanto na formação do professor como em sua rotina letiva.
Uma das vertentes de pesquisa realizada no interior desse grupo de estudos se relacionou com o projeto “Análise da Produção Escrita como Oportunidade para o Desenvolvimento Profissional de Professores de Matemática” contemplado pela Chamada Universal do Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPQ), de 2012. Esse projeto consistiu na realização de um evento de extensão5 (interno à Universidade Estadual de Londrina - UEL, Brasil), que tinha como um de seus objetivos: “investigar como professores que ensinam matemática na Educação Básica lidam com a elaboração de uma Trajetória Hipotética de Aprendizagem (THA)”, na perspectiva de Simon (1995). Para cumprir este objetivo (dentro do “projeto maior”6 de pesquisa) ofertamos, em um evento de extensão, uma Oficina de Formação Continuada para a qual tínhamos como intenção que os docentes, em formação continuada, vivenciassem por meio dela a prática e experiência de: (1) analisar produções escritas de estudantes e (2) elaborar trajetórias de aprendizagem, a partir das quais fosse promovido um espaço de debate, formação e trocas de experiências.
Nesse sentido, o objetivo do presente estudo, está relacionado à segunda intencionalidade descrita anteriormente, ou seja, a de descrever e analisar os elementos constituintes7 das Trajetórias Hipotéticas de Aprendizagem (THA), elaboradas por professores que ensinam matemática, em um contexto de formação continuada. Como objetivos específicos deste estudo, buscaremos:
inventariar quais foram os elementos constituintes utilizados pelos docentes em formação na elaboração das THA, que mereceram destaque na produção deles,
associar os elementos inventariados aos quatro domínios do “Conhecimento matemático para o ensino” (Ball & Bass, 2003; Ball, Thames, & Phelps, 2008),
e realizar alguma reflexão e análise sobre as produções escritas e os relatos que os professores apresentaram em suas THA.
O professor ao trabalhar com a elaboração de Trajetórias Hipotéticas de Aprendizagem tem a possibilidade de estabelecer uma visão geral do que poderá desenvolver com os estudantes, pois ela retrata uma visão das tomadas de decisões do professor a respeito dos conteúdos e tarefas e, permite entender como os processos de ensino e de aprendizagem podem ocorrer (Rossetto, 2016).
O trabalho em grupo, em nosso caso, com 16 professores que ensinavam matemática e três professoras formadoras, permitiu um espaço de produção de diálogos, trocas, afetos e possibilidades para todos os participantes do grupo. Não se trata de um professor formador (que trabalha na Universidade) ensinar um professor que se constitui como aprendiz, em uma formação continuada (que trabalha na Educação Básica). Essas, entre outras considerações, são consideradas em nosso estudo. Talvez, como Larrosa (2014) nos inspira na epígrafe, que vivências, pensamentos, aprendizados podem ser produzidos, para além de uma perspectiva do ensino.
Análise da produção escrita e o desenvolvimento profissional de professores
A análise da produção escrita é um meio para conhecer modos como alunos e professores lidam com problemas matemáticos. Por meio da análise de trabalhos escritos, podemos conhecer o modo como alunos e professores lidam com a resolução de problemas matemáticos, que estratégias e procedimentos matemáticos apresentam em suas respostas em questões abertas de matemática (Buriasco, 2004). Dentre as diversas possibilidades para conhecer a atividade matemática, a análise da produção escrita se apresenta como um caminho promissor na Educação Matemática, pois, por um lado, é foco de diversas pesquisas, o que oportuniza outros olhares para a sala de aula e, por outro, está ao alcance dos professores da Educação Básica, pois pode ser implementada a partir das provas escritas, trabalhos e qualquer material que ofereça algum tipo de registro escrito.
Vários trabalhos apontam possibilidades da análise da produção escrita como meio de leitura a respeito das maneiras como os alunos interpretam enunciados de questões, quais são os entraves e potencialidades do contexto que circunscreve esses enunciados, quais obstáculos relacionados à linguagem e ao modo como ela é estruturada em um problema (Cooper & Harries, 2002, 2003; D’Ambrosio, Kastberg, & Lambdin, 2007; Viola Dos Santos, Buriasco, & Ferreira, 2010).
Estudos desenvolvidos no interior do GEPEMA (Buriasco, 2004; Dalto & Buriasco, 2009; Ferreira, 2009; Viola Dos Santos & Buriasco, 2009), a respeito da ideia de avaliação como prática de investigação, tomando a análise da produção escrita como possibilidade de implementação, apontam na direção de que professores podem realizar interpretações e reflexões a respeito de trabalhos desenvolvidos pelos alunos em sala de aula e que essas ações podem oferecer ‘retratos’ e leituras dos processos de ensino e de aprendizagem. ‘Retratos’ de um processo dinâmico, em tempos e condições diferentes, que podem possibilitar questionamentos sobre qual matemática os alunos aprendem, quais entendimentos têm do que é trabalhado em sala de aula, quais dificuldades apresentam e, por conseguinte, para os professores, que tipos de intervenções eles podem elaborar.
Há, na literatura em Educação Matemática, vários trabalhos que apresentam o potencial da análise da produção como um caminho para conhecer, de modo detalhado, a atividade matemática dos alunos, como citado anteriormente. Dessa maneira, um caminho a ser trilhado é o de investigar potencialidades da análise da produção escrita8 como oportunidade para a formação continuada de professores de matemática. Nesse sentido, algumas das questões que nos inquietam na pesquisa consiste em saber: como a análise da produção escrita pode ser realizada e implementada por professores da Educação Básica em suas salas de aulas? Como ela pode servir de mote para o desenvolvimento profissional de professores em formação e em serviço? De que modo a análise da produção escrita pode oferecer conhecimentos para professores lidarem com demandas matemáticas de seus alunos em sala de aula?
Um crescente número de pesquisas a respeito dos conhecimentos adequados e necessários para a prática profissional do professor de matemática buscam superar a dicotomia: conteúdo versus metodologia. Vários pesquisadores (Ball & Bass, 2003; Ball, et al., 2008; Ma, 2009; Lins, 2006; Rowland, 2008; Watson, 2008) têm apresentado diferentes sistematizações a respeito de conhecimentos: pedagógico, matemático, do currículo, a respeito dos alunos e suas dificuldades, dos recursos de trabalho do professor. A partir de demandas da prática do professor que ensina matemática, essas caracterizações buscam construir uma especificidade do conhecimento que é relativa ao trabalho do educador matemático. Ao encontro dessas pesquisas, a análise da produção escrita pode oferecer subsídios para essas caracterizações, bem como uma possibilidade de implementação de uma prática investigativa que ofereça condições dos professores construírem essas particularidades em suas práticas.
O trabalho de Kazemi e Franke (2004) apresenta resultados de uma pesquisa com um grupo de professores investigando coletivamente produções escritas de alunos. Segundo as autoras, os professores desenvolveram um profundo conhecimento sobre o pensamento matemático de seus alunos, trabalhando coletivamente e investigando suas produções escritas. As autoras afirmam que uma primeira mudança no trabalho com os professores foi em relação à atenção dada aos detalhes das produções escritas e, consequentemente, à atividade matemática dos alunos. Uma segunda, foi que os professores começaram a desenvolver possíveis trajetórias instrucionais para o trabalho em sala de aula. Como afirmam Kazemi e Franke,
o uso da produção escrita dos alunos tem um potencial de influenciar o discurso profissional dos professores sobre o ensino e a aprendizagem, engajá-los em ciclos de experimentação e reflexão e mudar o foco, de uma pedagogia geral para uma particularmente conectada a seus próprios alunos. (Kazemi & Franke, 2004, p. 204)
Assim, consideramos que a análise da produção escrita pode contribuir para a formação de professores de matemática, em aspectos relativos ao “Conhecimento Matemático para o Ensino” (Ball & Bass, 2003), por exemplo. Ela pode contribuir para o desenvolvimento de
um conhecimento matemático ‘decorrente do ensino’, para os professores, em outras palavras, um conhecimento matemático necessário para executar tarefas recorrentes do ensino de matemática para os alunos. (Ball et al., 2008, p. 399)
Os autores citados caracterizam esse conhecimento, específico dos professores de matemática, por meio de quatro domínios: conhecimento comum do conteúdo, conhecimento especializado do conteúdo, conhecimento do conteúdo e dos estudantes, e conhecimento do conteúdo e do ensino.
O primeiro domínio, conhecimento comum do conteúdo, é caracterizado como o conhecimento e habilidades matemáticas que são utilizadas em outros contextos além do ensino. Os professores precisam conhecer a resposta correta de uma adição de números representados na forma fracionária, por exemplo. Eles precisam reconhecer quando o livro apresenta uma definição incorreta. Para os autores, “o comum, nesse domínio, sugere que qualquer pessoa tem este conhecimento e que ele não é específico do ensino” (Ball et al., 2008, p. 399).
Os autores caracterizam o segundo domínio, conhecimento especializado do conteúdo, em relação às habilidades e conhecimentos matemáticos específicos do ensino. Este domínio é característico da prática pedagógica do professor. Entre outras características o professor necessita compreender diferentes interpretações das operações; diferentes interpretações para a ideia de subtração e divisão, por exemplo; eles precisam saber “desempacotar” o conhecimento matemático para poder auxiliar na compreensão dos conceitos pelos alunos; precisam ser capazes de falar explicitamente sobre como a linguagem matemática é utilizada; e precisam saber utilizar diferentes representações matemáticas em diferentes contextos (Ball & Bass, 2003; Ball et al., 2008).
O terceiro domínio, conhecimentos do conteúdo e dos alunos, é “um conhecimento que combina saberes sobre os estudantes e a matemática. Professores precisam antecipar o que provavelmente os alunos pensam e em que eles podem se confundir” (Ball et al., 2008, p. 401). Nesse domínio os professores precisam ser capazes de escutar e interpretar as ideias incompletas dos alunos; promover interações entre compreensões matemática específicas e o modo de pensamento dos alunos. O conhecimento do professor nesse domínio é “um amálgama do conhecimento sobre o conteúdo e sobre os estudantes, que envolve uma ideia ou procedimento matemático particular e a familiaridade com o que os alunos pensam ou fazem” (Ball et al., 2008, p. 401).
O quarto domínio diz respeito aos conhecimentos do conteúdo e do ensino. Ele combina conhecimentos em relação ao conteúdo e também ao ensino desse conteúdo. Segundo os autores, “cada tarefa requer uma interação entre uma compreensão matemática específica e uma compreensão das questões pedagógicas que afetam a aprendizagem dos alunos” (Ball et al., 2008, p. 401). Neste domínio estão questões relativas à utilização de uma determinada linguagem ou metáfora que pode ajudar ou dificultar na aprendizagem de determinados tópicos matemáticos. Semelhantemente ao terceiro domínio, “o conhecimento do conteúdo e do ensino é um amálgama que envolve uma ideia ou procedimento matemático particular e uma familiaridade com princípios pedagógicos para o ensino de um tópico particular” (Ball et al., 2008, p. 402).
Acreditamos que esses domínios do “Conhecimento Matemático para o Ensino”, podem ser desenvolvidos em contextos formativos com professores da Educação Básica, em atividades de análises de produções escritas de alunos e atividades de produções escritas realizadas pelos próprios docentes. Ao encontro dessas hipóteses, uma das intenções subjacentes ao trabalho realizado com os professores na Oficina de Formação continuada era o de investigar contribuições do trabalho com análise da produção escrita com professores da Educação Básica para a construção/desenvolvimento desses domínios, e consequentemente, um desenvolvimento profissional de professores em formação inicial e continuada. A estratégia utilizada pelas professoras formadoras na Oficina de Formação Continuada promovida foi a de sugerir aos docentes em formação a elaboração de Trajetórias Hipotéticas de Aprendizagem, sobre as quais iremos tecer considerações na próxima seção.
Trajetórias hipotéticas de aprendizagem
Uma das ações desenvolvidas no âmbito da pesquisa realizada pelo GEPEMA esteve relacionada com a elaboração de THA por professores de Matemática. Assumimos como hipótese de trabalho que a elaboração de THA oportuniza uma reflexão aos professores sujeitos da pesquisa sobre essa experiência e podem desvelar aspectos sobre “Conhecimento matemático para o ensino”. Desencadear um ambiente colaborativo de aprendizagem reflete em fazer com que a reflexão sobre a experiência seja crítica e atenta ao próprio conhecimento, para que o indivíduo desenvolva por si seu processo de aprender. Esse contexto experiencial faz emergir uma produção de ideias e sentidos que pode se tornar mais familiar tanto para o professor quanto para o aluno. Nesse sentido, encontramos apoio nos princípios da elaboração de THA baseada em Simon (1995). Segundo esse autor, a expressão Trajetória Hipotética de Aprendizagem (THA) é utilizada
tanto para referir à previsão do professor como para a trajetória que possibilitará a aprendizagem. É hipotética, porque a verdadeira trajetória de aprendizagem não é cognoscível de antecedência. Isso caracteriza uma expectativa. A aprendizagem individual dos estudantes ocorre de forma idiossincrática, embora muitas vezes em trajetos semelhantes. (Simon, 1995, p. 135)
Na tentativa de tentar responder à questão: “como os professores de matemática podem promover a construção de ideias matemáticas que a comunidade de matemáticos levou milhares de anos para desenvolver?”. Simon (1995) considerou o planejamento do professor como um fator essencial, uma vez que dentre suas responsabilidades está o planejamento. A THA, nesse sentido, é entendida como uma alternativa para o professor em sala de aula e é constituída por três componentes:
1. o objetivo do professor com direções definidas para a aprendizagem de seus alunos;
2. as atividades de ensino;
3. o processamento hipotético de aprendizagem (uma suposição de como o pensamento e o entendimento dos alunos serão colocados em ação no contexto de aprendizagem das atividades). (Simon, 1995, p. 136)
A Figura 1 apresenta um esquema do ciclo de ensino sugerido por Simon (1995) que sugere como a THA pode ser reelaborada a partir de sua implementação em sala de aula. A THA pode ser entendida como um planejamento detalhado, em que o professor poderá, caso ocorram imprevistos, repensá-la, modificá-la, pois as interações professor e aluno e as observações do professor fazem com que isso acorra. Essa modificação da THA não ocorre somente durante a sua elaboração, mas pode ser feita em um ou todos os três componentes da trajetória hipotética de aprendizagem: nos objetivos, nas atividades, ou no processo hipotético de aprendizagem (Simon, 1995).
A elaboração de uma THA permite ao professor: maior segurança no gerenciamento da elaboração e na execução da proposta; prever perguntas que possam levar os alunos a refletirem, pensarem a respeito da tarefa; tomar decisões a respeito dos conteúdos e das tarefas; prever uma trajetória que possibilitará a aprendizagem; construir diálogos hipotéticos com os alunos; e alterar e modificar todos os três componentes da trajetória de aprendizagem (Rosseto, 2016).
Uma vez definido o objetivo de aprendizagem, a elaboração de uma trajetória hipotética de aprendizagem envolve a geração de um processo de aprendizagem hipotético de um conjunto particular de tarefas. Enquanto os objetivos de aprendizagem fornecem uma direção para a elaboração da trajetória hipotética de aprendizagem, a seleção de tarefas e as hipóteses sobre o processo da aprendizagem dos estudantes são interdependentes. Segundo Simon e Tzur (2004), as tarefas são selecionadas com base nas hipóteses que o professor tem quanto ao processo de aprendizagem, e a hipótese do processo de aprendizagem está baseada nas tarefas que estarão envolvidas. Estes autores apresentam algumas questões em que o professor pode pensar para a criação desse processo, como exemplo: quais tarefas, atualmente disponíveis para os estudantes, podem ser a base para que eles consigam alcançar os objetivos de aprendizagem? Eles argumentam que o “educador matemático precisa de uma compreensão dos processos de aprendizagem e do papel das tarefas matemáticas no processo de aprendizagem” (Simon & Tzur, 2004, p. 92). A partir dessa reflexão, o professor pode buscar em seus materiais qual tarefa traz possibilidades para que ele alcance seus objetivos.
Depois de estabelecer o(s) objetivo(s) de aprendizagem e selecionar as tarefas, o professor avalia o trabalho que desenvolveu e tem a possibilidade de reformular sua trajetória hipotética de aprendizagem (Simon, 1995). Para tanto, ele pode considerar as possíveis dúvidas que os estudantes apresentem enquanto tentam resolver as tarefas. Ao levantar essas dúvidas, o professor também antecipa as possíveis respostas para que os estudantes consigam compreender os detalhes que os deixaram confusos.
A elaboração de uma trajetória hipotética de aprendizagem “antes do ensino” na sala de aula é um processo pelo qual o professor desenvolve um plano de atividades para ser realizado em sala de aula por seus estudantes. Contudo, ao interagir com os estudantes e observá-los, o professor e os estudantes constituem uma experiência, que pela sua natureza social, é diferente daquela antecipada pelo professor. Nesse contexto, as ideias do professor sobre o conhecimento dos estudantes podem alterar-se e ele tem a possibilidade de modificar a trajetória hipotética de aprendizagem que havia elaborado (Simon, 1995).
De acordo com Gómez, González e Lupiáñez (2007), o conhecimento do professor, sua experiência e a literatura disponível são as fontes básicas para que ele possa elaborar uma trajetória hipotética de aprendizagem que apoie seu planejamento. Ao elaborar uma trajetória hipotética de aprendizagem, o professor planeja possíveis situações e rotas pelas quais a aprendizagem pode ocorrer no contexto de tarefas particulares. Nesse sentido, corrobora-se com Pires (2009, p. 164) ao afirmar que “os jovens professores precisam de conhecimentos sobre os saberes dos alunos, para gerar trajetórias hipotéticas de aprendizagem e análises conceituais para que possam ensinar Matemática”.
Alguns estudos têm apontado para a elaboração de Trajetórias Hipotéticas de Aprendizagem como oportunidade para a formação do professor de Matemática (Ivars et al., 2018; Sztajn et al., 2012; Wilson et al., 2014; Wilson et al., 2017).
Na pesquisa de Sztajn et al. (2012), os autores tomam como premissa que as Trajetórias de Aprendizagem utilizadas na formação fornecem quatro estruturas altamente utilizadas para o ensino da matemática, a saber: conhecimento matemático para o ensino, análise de tarefas, discurso como facilitador e práticas de ação e avaliação formativa. Eles apresentam dois esquemas na tentativa de: (1) conceitualizar o ensino em torno das Trajetórias de Aprendizagem, (2) definir componentes da instrução baseados em Trajetórias de Aprendizagem. Este segundo se aproxima do estudo que apresentamos aqui, ao associar os elementos constituintes das Trajetórias Hipotéticas de Aprendizagem analisadas com os quatro domínios do “Conhecimento matemático para o ensino” (Ball & Bass, 2003; Ball et al., 2008).
Em Wilson et al. (2014), os autores relatam uma experiência na qual examinam o design de um programa criado para apoiar a aprendizagem de professores em uma trajetória de aprendizagem realizando uma reinterpretação a partir da perspectiva do conhecimento matemático para o ensino (Ball et al., 2008). Os resultados indicaram que as tarefas de aprendizagem profissional com foco no conhecimento do conteúdo pedagógico presente nas trajetórias de aprendizagem permitem a aprendizagem do professor sobre o “conhecimento do conteúdo”.
Ivars et al. (2018) concluem a partir de sua pesquisa que o uso de uma trajetória de aprendizagem hipotética como um guia para interpretar o pensamento matemático dos alunos pode melhorar o discurso dos professores em formação. No estudo destes autores, 29 professores em formação participaram de um ambiente de aprendizagem em que tiveram de interpretar o pensamento dos alunos sobre o conceito de fração usando uma trajetória de aprendizagem hipotética como guia. Segundo estes autores, essa ação de formação ajudou os professores a desenvolver um discurso mais detalhado ao interpretar o pensamento matemático dos alunos, aprimorando suas habilidades de “perceber”, as quais estavam ligadas ao conhecimento do conteúdo matemático dos professores em formação.
Na tentativa de dialogar com esses pressupostos teóricos, apresentamos o relato de um estudo que teve a elaboração de THA como um contexto formativo em uma Oficina para Formação Continuada de professores que ensinam matemática.
Procedimentos metodológicos
Nesse trabalho realizamos uma pesquisa qualitativa, visto a natureza dos nossos dados e nossas intenções. Algumas características básicas dessa abordagem de pesquisa são a íntima relação do pesquisador com o pesquisado (resultando em uma não neutralidade); um maior interesse no processo analisando as informações de maneira intuitiva; a descrição dos dados tendo como foco o particular buscando um maior nível de profundidade de compreensão; a não intenção de comprovação ou refutação de algum fato; a impossibilidade de estabelecer regulamentações (Bogdan & Biklen, 1994; Garnica, 2004). Essa pesquisa seguiu uma abordagem qualitativa de cunho interpretativo sob as orientações presentes na análise de conteúdo (Bardin, 2004), à luz de pressupostos teóricos da (1) análise da produção escrita, do (2) desenvolvimento profissional docente e (3) das trajetórias hipotéticas de aprendizagem.
O objetivo principal do presente estudo é de descrever e analisar os elementos constituintes das Trajetórias Hipotéticas de Aprendizagem (THA), elaboradas por professores que ensinam matemática, em um contexto de formação continuada.
A análise da produção escrita9 (1) é aqui utilizada, primariamente, como recurso para analisar as produções dos professores sujeitos da pesquisa dentro da THA, muito embora, ela tenha sido utilizada, também, como recurso para os sujeitos da pesquisa elaborarem suas THA.
Para o estudo que aqui se apresenta, optamos por nos debruçar apenas em descrever os resultados obtidos sobre os elementos constituintes que emergiram da elaboração das THA, muito embora, a análise da produção escrita tenha permeado e sustente todo o processo de elaboração das THA, como o exemplo que será apresentado mais adiante no Quadro 2. A “análise da produção escrita” é utilizada por nós, pesquisadores, como recurso analítico para fazer a leitura das produções dos professores elaboradores das THA apresentadas.
Aspectos do desenvolvimento profissional docente (2) na análise que será apresentada estarão associados ao olhar dos quatro domínios do “Conhecimento matemático para o ensino” de Ball e seus colaboradores (Ball & Bass, 2003; Ball et al., 2008).
E, por fim, a elaboração das trajetórias hipotéticas de aprendizagem (3) é utilizada como instrumento de formação bem como de coleta de dados da pesquisa, pois são elas (as THA) nosso objeto de estudo.
As informações para o desenvolvimento desta pesquisa foram coletadas em uma Oficina de Formação Continuada, que ocorreu no âmbito de um evento de extensão.
Participaram desta oficina 16 professores que ensinam Matemática da Educação Básica que aceitaram o convite das formadoras; três professoras do Departamento de Matemática da Universidade Estadual de Londrina (denominadas “formadoras”), três mestrandos do Programa de Pós-Graduação em Ensino de Ciências e Educação Matemática - PECEM, aqui denominados colaboradores da oficina e um aluno da graduação que desenvolvia seu projeto de iniciação científica.
Uma das atividades desenvolvidas na Oficina de Formação Continuada foi a elaboração de Trajetórias Hipotéticas de Aprendizagem por professores que ensinavam matemática. Tínhamos como hipótese que os professores em formação colocariam em prática, nas trajetórias, alguns procedimentos associados à “análise da produção escrita”, cujo tema tinha sido amplamente discutido e explorado nos encontros presenciais da oficina. Além disso, tínhamos também como hipótese que as escritas dos sujeitos da pesquisa na elaboração das THA desvelariam aspectos do desenvolvimento profissional dos mesmos.
As THA foram elaboradas pelos sujeitos da pesquisa em duplas durante os encontros presenciais da Oficina de Formação Continuada e, em parte, fora dele, em encontros entre as duplas. Tivemos como produto final desta ação 8 trajetórias elaboradas em duplas. É sobre as produções escritas dos professores presentes nessas THA por eles elaboradas que teceremos nossas análises e considerações na seção seguinte. Para situar as trajetórias e os sujeitos da pesquisa, decidimos codificá-los como T1, T2, T3, ..., para especificar as trajetórias distintas.
Para explicitar o contexto da elaboração dessas trajetórias é importante relatar que as professoras formadoras propuseram na Oficina de Formação Continuada outros temas e tarefas que motivaram o debate coletivo, e que podem ter influenciado fortemente algumas das decisões dos professores em formação na construção de suas trajetórias.
Análises e inferências
Nesta seção objetiva-se descrever e analisar os elementos constituintes das Trajetórias Hipotéticas de Aprendizagem (THA), elaboradas por professores que ensinam matemática, em um contexto de formação continuada. Buscaremos apresentar um inventário dos elementos utilizados pelos docentes em formação na elaboração e proposição das THA, os quais chamaremos de elementos constituintes das THA; associar esses elementos inventariados aos quatro domínios do “Conhecimento matemático para o ensino” (Ball & Bass, 2003; Ball et al., 2008); e realizar alguma reflexão e análise sobre as produções escritas e os relatos que os professores apresentaram em suas THA. Para isso fizemos uma leitura dos elementos que compuseram cada uma das trajetórias elaboradas, que são apresentados no quadro 1.
Nas linhas estão dispostos cada um dos elementos distintos que os docentes julgaram importantes de apresentar em suas produções. Nas colunas enumeramos a ordem em que estes elementos aparecem na trajetória no sentido “linear” da leitura, para termos uma ideia das escolhas que eles fizeram, ou, nenhuma marcação quando não são apresentados declaradamente10. Associamos as letras (a, b, c,...) aos números, para indicar os casos nos quais os elementos escolhidos apareceram simultaneamente, por exemplo: 08a e 08b, indicam que os dois elementos citados aparecem juntos, sem uma ordem específica.
Quadro 1: Elementos constituintes das THA apresentados pelos professores sujeitos da pesquisa
| Elementos constituintes das Trajetórias | T1 | T2 | T3 | T4 | T5 | T6 | T7 | T8 |
|---|---|---|---|---|---|---|---|---|
| Apresentação | 01 | 01 | 02 | |||||
| Introdução | 01 | 01 | 01 | 01 | ||||
| Objetivo Geral | 02 | 05 | ||||||
| Objetivos Específicos | 03 | 02 | 02 | 03 | 03 | 03 | 03 | |
| Intenções | 04 | 03 | 04 | 04 | 04 | |||
| Tempo Estimado | 03 | |||||||
| Conteúdos Estruturantes | 05 | 03 | 05 | |||||
| Conteúdos Específicos | 06 | 04 | 04 | 02 | 06 | 02 | 02 | |
| Estratégia Metodológica | 07 | 06 | 05 | |||||
| Contrato Didático | 08 | 05 | ||||||
| Enunciado das tarefas | 09 | 02 | 05 | 04 | 06 | 07 | 01 | 01 |
| Procedimentos de ensino | 10 | 06 | 04a | 05a | ||||
| Possíveis resoluções | 11 | 07 | 07 | 06 | 07 | 08a | 04b | 05c |
| Possíveis dúvidas - em um diálogo hipotético | 12 | 07 | 08a | 08b | 04c | 05b | ||
| Sistematização | 08 | 08 | 07 | 08b | 04d | |||
| Considerações Finais | 13 | 09 | 09 | 08 | 09 | 05 | ||
| Referências | 14 | 10 | 10 | 09 |
Começamos nossa análise pela observação dos três elementos básicos que compõem uma THA segundo Simon (1995), a saber: o objetivo do professor com direções definidas para a aprendizagem de seus alunos, tarefas de ensino e o processamento hipotético de aprendizagem. Verificamos que estes três elementos essenciais foram contemplados em todas as trajetórias elaboradas, podendo ser observados mais especificamente nos itens C e D (objetivo geral e específico); no item K (enunciados das tarefas) e, M e N (possíveis resoluções e possíveis dúvidas). Usamos a expressão “mais especificamente” na frase anterior, porque estes elementos são os que mais evidentemente caracterizam, a nosso ver, a constituição de uma THA. Porém, cabe salientar que o chamado “processamento hipotético”, segundo Simon (1995), também pode ser observado em outros elementos que são apresentados pelos docentes e que serão discutidos aqui.
No que diz respeito aos itens A e B, Introdução e Apresentação, identificamos que os docentes os utilizaram com o objetivo de fornecer informações aos leitores a respeito do que se tratava a proposta apresentada. Eles teceram comentários sobre aspectos teóricos da THA, sobre o contexto de elaboração das THA (Oficina de Formação Continuada) e, outros fatores, como exemplos: qual público seria destinada aquela trajetória, o ano escolar de implementação, e também, algumas justificativas que motivaram a apresentação do trabalho, como pode ser observado na escrita da produção T4:
Esta produção tem a intenção de apresentar uma proposta para o ensino de matemática inovador, matematizando conteúdos de forma que leve o aluno a pensar, problematizar, por meio de um modelo de ensino baseado na Trajetória Hipotética de Aprendizagem, formulada por Martin Simon (1995) tanto para fazer referência ao prognóstico do professor como para o caminho que possibilitará o processamento da aprendizagem. (T4, dados da pesquisa)
Ao explicitar na “Introdução” para qual ano escolar aquela trajetória em específico seria dedicada, os professores demonstram aspectos dos “conhecimentos do conteúdo e do ensino”, uma vez que “cada tarefa requer uma interação entre uma compreensão matemática específica e uma compreensão das questões pedagógicas que afetam a aprendizagem dos alunos” (Ball et al., 2008, p. 401). Os professores precisam reconhecer em qual nível cada tarefa pode ser adequada, e de qual público ela pode extrair maior debate, aprofundamento de ideias e versatilidade.
Os itens C, D e E denotam a importância dada pelos docentes em apresentar os objetivos com a THA proposta. Cabe relatar que durante a Oficina de Formação Continuada, os professores sujeitos da pesquisa tiveram a oportunidade de estudar teoricamente noções sobre a THA de Simon (1995) e participaram de seminários e debates coletivos sobre este assunto, na tentativa de encontrar “um lugar comum” para falar sobre a produção delas. Portanto, era de se esperar que os três elementos essenciais da THA fossem apresentados em suas produções. Além disso, observa-se que em algumas trajetórias encontramos os elementos “objetivo geral”, “objetivos específicos” e “intenções”. Um amplo debate havia sido realizado no âmbito dos encontros presenciais da Oficina de Formação Continuada. Essa distinção entre objetivos e intenções pode ser explicitada pelo seguinte excerto presente na produção de T1 (Figura 2).
Nessa perspectiva, o grupo como um todo chegou ao consenso de que “os objetivos” são as ações que são esperadas dos alunos, sujeitos da THA, e eles podem ser de dois tipos: Geral e Específicos. Já as intenções estão mais intimamente ligadas às ações dos docentes para fazer com que os alunos atinjam aos objetivos esperados (Figura 3).
Ao encontro desses itens identificamos aspectos do quarto domínio “conhecimento do conteúdo e do ensino” (Ball et al., 2008, p. 402), pois os objetivos, intenções e conteúdos estão intimamente ligados com a competência de reconhecer em qual contexto pedagógico eles se aplicam e, neste caso em particular, como se relacionam com a tarefa proposta e suas demandas para o ensino de um tópico em particular.
O item F (tempo estimado) esteve presente em apenas uma das trajetórias elaboradas (T4). Vale ressaltar que não existe uma “receita” única e explícita sobre o modo como as trajetórias devem ser desenvolvidas ou que elementos devem aparecer nela, salvo os três elementos citados por Simon (1995) que são uma espécie de “pilares”. Em alguns momentos das discussões, para explicitar a ideia de uma trajetória hipotética de aprendizagem, associamos a um recurso totalmente rotineiro e comum nas práticas docentes: a elaboração de planos de aula. Nesses, é comum que os docentes apresentem este elemento.
Nessa mesma interpretação, acreditamos que os itens G e H (conteúdos estruturantes e específicos) tenham surgido. Ao estabelecer/reconhecer quais conteúdos circunscrevem a tarefa proposta, os professores tiveram uma maior abertura para realizar as hipóteses no processamento hipotético que era esperado deles. Em especial, na Oficina de Formação Continuada, houve debate sobre as diferenças entre “conteúdos estruturantes” e “conteúdos específicos”, presentes em documentos orientadores para o ensino, como os PCN (Brasil, 1998) e DCE (Paraná, 2008).
Nestes elementos reconhecemos a importância do segundo domínio “conhecimento especializado do conteúdo”, uma vez que ele pode subsidiar as tomadas de decisão dos docentes. O professor necessita ter um domínio e conhecimento consistente do conteúdo para delimitar os objetivos de uma proposta pedagógica. Sem esse conhecimento, os objetivos para o ensino correm o risco de serem inúteis, improdutivos e até mesmo obsoletos. Os docentes precisam saber explorar o conhecimento matemático para poder auxiliar na compreensão dos conceitos pelos alunos (Ball et al., 2008).
Os itens I e J (estratégia metodológica11 e contrato didático), a nosso ver, foram fortemente influenciados por outras experiências formativas que os professores (em formação) estavam vivendo na universidade. Mais especificamente, os professores sujeitos da pesquisa tiveram a oportunidade de estudar teoricamente a Resolução de problemas e, o exemplo disso é que, T4 cita que a estratégia metodológica adotada na trajetória seria fundamentada em Allevato e Onuchic (2009). Em outras trajetórias, os sujeitos não fundamentaram a Resolução de Problemas ou deram destaque nela como um item constituinte, porém, nas análises, pudemos inferir que eles encaminharam seu processamento hipotético nessa perspectiva, como o excerto de T7 pode sugerir (Figura 4).
Os itens I e J vão ao encontro do quarto domínio que diz respeito aos “conhecimentos do conteúdo e do ensino” (Ball et al., 2008), pois ele combina conhecimentos em relação ao conteúdo e também ao ensino desse conteúdo. Este domínio envolve, a nosso ver, reconhecer a utilização de uma determinada estratégia metodológica oportunizadora de aprendizagem em um contexto desejado. Implica também reconhecer que a negociação de um “contrato didático” pode ajudar ou facilitar na aprendizagem de determinados tópicos matemáticos.
Observa-se que o item K (enunciado das tarefas) está presente em todas as trajetórias e isso, além de esperado, era praticamente obrigatório, uma vez que os professores em formação tinham como meta elaborar suas trajetórias a partir de uma tarefa de matemática. Nessas trajetórias em particular, os professores (em duplas) elaboraram uma trajetória a partir de apenas uma tarefa (denominada por Simon;1995 como atividades de ensino). Foi a partir dos enunciados dessas tarefas (no total de oito tarefas: uma para cada dupla) que eles elaboraram suas THA.
Os itens L, M, N e O (procedimentos de ensino, possíveis resoluções, possíveis dúvidas, sistematização) foram interpretados como sendo o núcleo do processamento hipotético de aprendizagem. Ao contrário deles, “conteúdos” e “objetivos”, por exemplo, foram quase que uma consequência imediata da “tarefa” propulsora da trajetória. Queremos salientar que uma tarefa que envolve essencialmente uma ideia de funções, não teria uma trajetória que pudesse se distanciar desse tema em seus conteúdos e objetivos. Por outro lado, os “procedimentos de ensino”, “possíveis resoluções”, “possíveis dúvidas” e meios de “sistematização” tomam rumos distintos, e mais hipotéticos possível, pois estão amalgamados nos conhecimentos e experiências que os sujeitos da pesquisa tiveram ao longo de suas vidas acadêmicas.
A Figura 4, apresentada anteriormente, ilustra um exemplo de como a dupla de T7 desenvolveu seus procedimentos de ensino. Já o elemento “possíveis resoluções” pode ser observado em todas as oito trajetórias elaboradas. Acreditamos que isso é um fator relevante para inferir que os professores em formação associaram o “caráter hipotético” de aprendizagem a este elemento, e, especialmente, por trazer no título o termo “possíveis”. Nesse elemento, os professores apresentam, em média, três ou quatro resoluções para a tarefa proposta, tentando diversificar em cada “possível resolução” as estratégias, os procedimentos, respostas e possíveis modos de lidar dos estudantes.
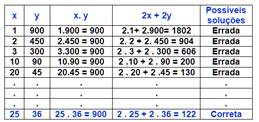
Como exemplo, a trajetória T2 se desenvolveu em torno de uma tarefa que requisitava noções de área e perímetro. As possíveis resoluções para esta tarefa abordaram procedimentos como: (1) tentativa e erro, (2) construção de tabelas, (3) desenvolvimentos aritméticos e (4) algébricos. Tanto as noções de “estratégias” quanto as de “procedimentos” estão associadas ao olhar da “análise da produção escrita” que é objeto de estudo do GEPEMA. Estas noções emergiram no contexto da Oficina de Formação continuada com estes professores e puderam ser observadas em suas trajetórias, como exemplificamos no quadro 2(apresentado na página seguinte).
A competência para explicitar possíveis resoluções, diferentes estratégias de abordagem de um problema tem uma íntima relação com o segundo domínio, “conhecimento especializado do conteúdo”. Como argumenta Ball e seus colaboradores, entre outras características, o professor necessita compreender diferentes interpretações das operações; diferentes interpretações para a ideia de subtração e divisão, por exemplo; precisam saber utilizar diferentes representações matemáticas que são mais adequadas em diferentes contextos (Ball & Bass, 2003; Ball et al., 2008). Ivars et al. (2018) sugerem que o desenvolvimento da habilidade de “perceber”12 o pensamento matemático dos alunos está vinculado ao conhecimento do conteúdo matemático dos professores em formação. Além disso, estes autores suspeitam ainda que o desenvolvimento da habilidade de perceber está associado à melhoria da qualidade do discurso profissional produzido pelos professores (Ivars et al., 2018). Nesse sentido, temos como suposição que a elaboração de THA pode colocar os professores em formação nesse movimento de “perceber” bem como o de melhorar seus discursos profissionais.
Quadro 2: Fragmentos da Trajetória de T2 que refletem a abordagem dada às Possíveis Resoluções para uma tarefa
Seis das oito das trajetórias também trazem o elemento “possíveis dúvidas”, acreditamos que na mesma direção de desenvolver o chamado “processamento hipotético”. A seguir apresentamos um exemplo que ilustra este elemento em T6 (Figura 5).
Ao encontro dessa perspectiva está o terceiro domínio “conhecimentos do conteúdo e dos alunos”, é um conhecimento que combina saberes sobre os estudantes e a matemática. Professores precisam antecipar o que provavelmente os alunos pensam e em que eles podem se confundir (Ball et al., 2008, p. 401). A competência para hipotetizar sobre contextos pedagógicos envolve processos de “antecipação”, que serão subsidiados pelas experiências escolares (ou não) que os docentes possuem. Nesse domínio, os professores precisam ser capazes de escutar e interpretar as ideias incompletas dos alunos; promover interações entre compreensões matemática específicas e o modo de pensamento dos alunos. O conhecimento do professor nesse domínio é “um amálgama do conhecimento sobre o conteúdo e sobre os estudantes, que envolve uma ideia ou procedimento matemático particular e a familiaridade com o que os alunos pensam ou fazem” (Ball et al., 2008, p. 401).
No que diz respeito ao elemento “Sistematização” (item O), observamos que ele aparece isolado nas trajetórias T2, T3 e T4 (existindo como um tópico específico e único para a tarefa), e aparece como um item diluído nas trajetórias T5 e T7, geralmente acompanhando cada possível resolução distinta. Aqui acreditamos que a forma como os docentes concebem o momento da “sistematização” foi um forte influente sobre o modo como organizaram suas trajetórias. Uma hipótese é que T3 e T4 apresentaram este elemento de forma isolada, pensando nas etapas da estratégia metodológica da Resolução de Problemas, segundo Allevato e Onuchic (2009), visto que eles a utilizaram declaradamente. O sucesso de uma proposta de sistematização de um conteúdo, a nosso ver, pode estar relacionado com um transitar híbrido entre o segundo e terceiros domínios de Ball, Thames e Phelps (2008), pois envolve tanto o conhecimento especializado do conteúdo quanto conhecimentos do conteúdo e dos alunos.
No item P (considerações finais) os professores autores das trajetórias geralmente expressam considerações mais sobre o trabalho desenvolvido no contexto da oficina de formação continuada, do que considerações específicas da trajetória que realizaram em particular. Essas considerações, em geral, foram na direção de: retomar o conceito teórico da THA pelas explicitações de Simon (1995); relatar as dificuldades que tiveram ao longo do processo da elaboração da THA; ressaltar as aprendizagens que tiveram neste processo (fala de T2, no Quadro 3); motivar outros docentes a elaborar THA (fala de T4, no Quadro 3); concluir que as THA se constituem como um recurso “articulador” de ideias; entre outros. No quadro 3 podemos ver alguns trechos que exemplificam essas considerações.
Quadro 3: Trechos que refletem exemplos sobre o elemento P “Considerações Finais”
| THA | Trechos captados nas “Considerações Finais” |
| T2 | “O envolvimento na realização de algumas tarefas, por meio da metodologia da Resolução de Problemas, utilizando a Trajetória Hipotética de Aprendizagem possibilita ao professor levar o aluno a construir conceitos e conteúdos matemáticos, proporcionando assim, uma maior aprendizagem, promovendo correções, possibilitando mudanças que favoreçam o entendimento dos alunos, ampliando seus conhecimentos e o nosso quanto professor”. |
| T3 | “A novidade para nós, enquanto professoras, foi que a partir de uma tarefa encontramos várias13resoluções e a partir delas desenvolvemos diversos conteúdos. Na busca dos conteúdos a serem trabalhados percebeu-se que um conduz a outro”. |
| T4 | “Desenvolver uma Trajetória Hipotética de Aprendizagem, permite ao professor estruturar seu planejamento prevendo situações, o que traz mais segurança, bem como possibilitar correções que possam favorecer a compreensão dos conceitos pelos alunos. Concordamos com Simon, que o professor deve assumir o papel de mediador da construção do conhecimento matemático, não sendo suficiente dividirmos a sala em equipes e deixarmos livres para resolver as questões, mas o professor deve fazer as intervenções necessárias para condução da tarefa a fim de se atingir o objetivo almejado. Assim, a THA possibilita ao professor a opção de construção de seu projeto baseado em suas hipóteses da melhor maneira de se planejar uma aula, pensando-se no processo de aprendizagem mais viável para os alunos”. |
| T5 | “Durante a elaboração das atividades da Trajetória Hipotética de Aprendizagem, observamos o quanto éramos conservadores em nossa prática em sala de aula, mesmo pensando que com diversas metodologias já estudadas e já sendo aplicadas. Vejo que através desta experiência no Projeto Universal14, muitos conceitos dos professores foram desconstruídos, ou seja, mudanças significativas ocorreram. Não voltaremos para a sala de aula da mesma forma de quando começamos este curso”. |
Observa-se na fala de T3 (Quadro 3) que os professores dão indícios do “perceber” o conhecimento do conteúdo matemático quando relatam que puderam visualizar nesta experiência realizada variados tipos de resolução para uma mesma tarefa, indo ao encontro do que é relatado na pesquisa de Ivars et al. (2018).
Por fim, temos o último item Q, que se trata das referências, nas quais os professores demonstram a preocupação em revelar as fontes nas quais se basearam para propor as trajetórias elaboradas. Esse é um detalhe muito importante que se destaca, pois os professores estavam inseridos em um ambiente acadêmico e mostraram respeitar a interlocução entre o estudo teórico e suas práticas e experiências docentes, representadas pelas produções que apresentaram e estudos que fizeram.
Algumas considerações finais
Uma contribuição da Oficina de Formação Continuada foi a elaboração de THA como um contexto formativo para oportunizar aspectos do desenvolvimento profissional de professores que ensinam matemática. Mais do que desvelar esses aspectos, o contexto colaborativo de formação oportunizado na Oficina de Formação Continuada permitiu o desenvolvimento profissional dos sujeitos da pesquisa. Em grupos, ou em duplas, eles se debruçaram sobre demandas intimamente relacionadas às suas práticas profissionais, as quais, poucas vezes, são discutidas e problematizadas em cursos de Licenciatura em Matemática. Outros estudos também foram realizados nessa intencionalidade e demonstram resultados favoráveis sobre o desenvolvimento profissional docente (Ivars et al., 2018; Sztajn et al., 2012; Wilson et al., 2014; Wilson et al., 2017). A seguir apresentamos algumas conclusões deste estudo.
Uma trajetória hipotética de aprendizagem é um planejamento (programa) bem detalhado do caminho, ou caminhos, da aprendizagem do estudante. O professor estabelece objetivos que quer que o estudante alcance, seleciona tarefas que farão que esses objetivos sejam alcançados e, por fim, hipotetiza como o estudante desenvolverá a tarefa para atingir os objetivos. Essas hipóteses são variadas e podem ser modificadas e, conforme pudemos observar nas THA elaboradas no contexto deste estudo, não há uma receita definida ou roteiro explícito de como pode ou deve ser realizada.
As possíveis perguntas e dúvidas previstas na elaboração da THA podem permitir ao professor maior segurança no gerenciamento da elaboração da proposta. Isto pôde ser evidenciado nas falas dos sujeitos participantes da pesquisa aqui relatada e, também, é uma inferência, uma vez que ao antecipar as dúvidas que os estudantes podem apresentar, o professor se coloca a questionar e refletir a própria prática, tarefas, recursos, o próprio conteúdo matemático em questão.
Ao relatar as hipóteses, professores podem utilizar diálogos hipotéticos com os alunos, para prever perguntas que possam levar os alunos a refletirem, pensarem a respeito da tarefa. Este foi o recurso mais utilizado pelos sujeitos da pesquisa para explicitar a forma como entendem um processamento hipotético dentro de uma THA.
De modo geral, os docentes sujeitos dessa pesquisa apresentaram estratégias e procedimentos da matemática escolar comumente trabalhada na Educação Básica. Estas estratégias e procedimentos se fizeram presentes ao descreverem as resoluções hipotéticas dos alunos dentro de suas THA.
Os elementos constituintes das THA elaboradas por eles se “aproximam” de suas práticas escolares. Isto significa que esses elementos fazem parte da rotina desses professores. O planejamento docente envolve praticamente todos os elementos observados, por exemplo, a delimitação dos objetivos, dos conteúdos, dos procedimentos de ensino, das tarefas. No entanto, usamos a palavra “aproximam” pelo fato de que, a abordagem dada a esse planejamento, nesse contexto, foi diferenciada, uma vez que os sujeitos da pesquisa explicitaram detalhadamente cada um desses elementos. Supomos que, na prática, dada a rotina de trabalho exaustiva dos professores brasileiros, esse planejamento com riqueza de detalhes dificilmente ocorre. Nesse sentido, por meio da análise da produção escrita que fizemos pudemos identificar aproximações dos elementos que chamamos de “constituintes” com os quatro domínios do “Conhecimento matemático para o ensino” (Ball & Bass, 2003; Ball et al., 2008) por acreditar que eles puderam desvelar aspectos do desenvolvimento profissional docente.
O Conhecimento Matemático para o Ensino exerce extrema influência nos modos de lidar com as tarefas que são previstas em uma THA. A quantidade de exemplos, possíveis resoluções, dúvidas hipotéticas, respostas e encaminhamentos dos docentes frente às dúvidas dos estudantes (hipotetizadas) podem influenciar no nível e aprofundamento de ideias apresentadas pelos docentes, que é consistente e coerente com a “bagagem” teórica e prática que construíram ao longo de seus anos escolares. Este é um tema que pode servir para futuras pesquisas.
As Trajetórias Hipotéticas de Aprendizagem elaboradas pelos sujeitos desta pesquisa revelam que eles inseriram em suas produções escritas elementos que foram tematizados e debatidos coletivamente na Oficina de Formação Continuada, indicando que a formação realizada exerceu alguma influência em seus modos de refletir suas práticas escolares.
Grupos de trabalho constituídos por diferentes professores que ensinam matemática e que atuam em diferentes níveis de ensino são espaços potentes para promover a formação docente, discussões e aprendizagem que podem impactar no desenvolvimento profissional e na atuação de professores que ensinam matemática. Grupos de trabalhos, análise de produções escritas e elaborações de trajetórias hipotéticas de aprendizagens oferecem possibilidades de organizar discussões, problematizações e produções de conhecimentos matemáticos para o ensino de professores que ensinam matemática. Esse trabalho vai na perspectiva de ampliar a ideia de ensino (alguém que já sabe e que se constitui como aquele que vai ensinar) e aprendizagem (alguém que não sabe e se constitui como aquele que vai aprender), na direção de construir espaços de aprendizagens (nos quais todos aprendem). Além disso, devem ser consideradas, nesse contexto, todas as demandas matemáticas e pedagógicas que se apresentam como um cenário para formação de professores que ensinam matemática.
Cabe salientar que nos restringimos a analisar uma primeira versão das THA elaboradas pelos professores sujeitos da pesquisa. Segundo a proposta de Simon (1995) seria desejável tornar essas trajetórias (apesar de hipotéticas) mais próximas da realidade através da implementação na prática, como um meio de avaliá-las e modificá-las conforme os sucessos e insucessos. Esta prática não foi realizada no contexto desse estudo, mas consideramos que pode ser um tema para futuras pesquisas.