As potencialidades da Teoria de Resposta ao Item na validade dos testes: Aplicação a uma prova de dependência-independência de campo

Maria João Vieira ^(*)

Rui Bártolo Ribeiro ^(*)

Leandro S. Almeida ^(**)

RESUMO

No presente estudo realizou-se uma análise aos itens da prova “Padrões” – teste de escolha múltipla informatizado que avalia a dependência-independência do campo – à luz dos modelos de um, dois e três parâmetros da Teoria de Resposta ao Item (TRI). Utilizou-se uma amostra de 1.918 candidatos ao Curso de Pilotagem Aeronáutica da Academia da Força Aérea Portuguesa. Analisou-se o ajustamento aos modelos logísticos de um (ML1), dois (ML2) e três parâmetros (ML3), concluindo-se que o primeiro modelo se ajustou a todos os itens que compõem a prova, o segundo apenas a sensivelmente metade dos itens, e o terceiro não chegou a cumprir as pré-condições. A análise dos resultados sugere que a principal razão do desajuste dos ML2 e ML3 se tenha ficado a dever à não unidimensionalidade do teste, ilustrando deste modo as exigências fundamentais da aplicação da TRI na construção e validação de provas psicológicas.

Palavras chave: Análise dos itens, Dependência-independência de campo, Teoria da Resposta ao Item (TRI), Validade dos testes.

 

ABSTRACT

In this paper analyses the items of “Padrões” test – a multiple-choice computerized test of field dependence-independence – considering the one, two or three parameters logistic models of Item Response Theory (TRI). A sample of 1918 candidates to an aeronautic course on Portuguese Air Force was considered. We analyzed the adjustment level for one parameter (1PL), two parameters (2PL) and three (3PL) parameters logistic models. Results show that 1PL adjusted to all items, 2PL adjusted to half, and 3PL didn’t allow the assurance of the previous conditions. Data analysis suggest that the first reason for 2PL and 3PL models maladjustment is the lack of unidimensionality, which can be considered as an illustration of the basic exigencies for IRT implementation on psychological test construction and validation.

Key words: Field dependence-independence, Item analysis, Item Response Theory (IRT), Tests validity.

 

 

INTRODUÇÃO

O livro de Lord e Novick (1968, citado por Embretson & Reise, 2000) pretendia revolucionar a metodologia seguida na construção e validação dos testes psicológicos, destacando várias potencialidades da “Teoria da Resposta ao Item” (TRI) na mensuração psicológica. Nesta teoria, também algumas vezes designada “Teoria do Traço Latente” (TTL), o nível do traço de um indivíduo é estimado a partir das respostas que ele dá aos itens que lhe são apresentados e não através da comparação do seu desempenho face à média e desvio-padrão dos resultados num qualquer grupo de referência (Embretson & Reise, 2000), sendo esta aliás a grande novidade do método.

A TRI está assente em vários pilares, nomeadamente: a forma específica das curvas características dos itens (CCIs); a independência local; a unidimensionalidade; e a função característica do item (FCC) (Embretson & Reise, 2000; Hambleton, Swaminathan, & Rogers, 1991; Yu, 2007). Deste conjunto de pressupostos ou condições prévias, importa aqui destacar a unidimensionalidade e a independência local dos itens de uma prova psicológica (Pasquali & Primi, 2003).

O postulado da independência local afirma que as respostas dadas por um mesmo sujeito a dois itens são independentes, desde que sejam mantidas constantes as aptidões que afectam o teste, à excepção da aptidão que está a ser medida (theta ou θ) (Pasquali & Primi, 2003). Em termos pragmáticos, este postulado tem uma implicação necessária à aplicação da TRI, ou seja, o desempenho do sujeito num item não afecta o seu desempenho nos restantes. A independência local diz-nos que se existir correlação, essa é causada por outros factores que não a aptidão. A partir do momento em que sejam mantidos constantes esses outros factores, o factor dominante (traço avaliado) passa a ser a única fonte de variabilidade, tornando-se assim as respostas independentes, dado que o sujeito responde aos itens apenas em função do seu θ (Pasquali, 2007; Pasquali & Primi, 2003).

Partindo do postulado da independência local chegamos também ao pressuposto da unidimensionalidade dos itens da prova. A TRI requer que todos os itens numa prova avaliem um único traço, ou seja, a prova deve ser unidimensional, pois de outra forma a sua análise deve ser feita por subconjuntos de itens ou dimensões. A questão da independência local implica o postulado da unidimensionalidade, uma vez que é o θ do sujeito a única causa ou factor latente da resposta dada (Pasquali & Primi, 2003).

Assim sendo, para uma correcta aplicação da TRI a um qualquer instrumento de medida psicológica, deve assumir-se a unidimensionalidade dos itens, ou seja, cada um dos itens mede apenas um traço latente (Wiberg, 2004). Extrapolando deste princípio, um participante com uma habilidade elevada no constructo que está a ser avaliado terá uma elevada probabilidade de responder correctamente ao item. Ao mesmo tempo, os itens que melhor avaliam a habilidade de um sujeito, são aqueles que exigem o nível de traço necessário para a correcta resolução equivalente ao nível geral de traço que esse mesmo sujeito possui. Por outras palavras, itens demasiado fáceis ou difíceis para um participante, contribuem muito pouco para estimar a sua habilidade (Green, Bock, Humphreys, Linn, & Reckase, 1984).

Dependência-independência de campo

O constructo dependência-independência de campo descreve duas formas distintas de processar informação e encontra-se entre os mais estudados no que diz respeito às dimensões dos estilos cognitivos (Guisande, Páramo, Tinajero, & Almeida, 2007). Os indivíduos dependentes de campo, tendencialmente, percebem o campo como um todo, têm dificuldade em separar a informação do seu contexto, e são mais facilmente influenciados por pistas externas. Já no outro extremo, os indivíduos independentes de campo, têm tendência para se focar em aspectos isolados, têm mais facilidade em separar a informação essencial do contexto, e são mais facilmente influenciados por pistas internas do que externas (Miyake, Witzki, & Emerson, 2001).

O teste “Padrões” permite-nos avaliar o construto dependência-independência de campo, tendo a singularidade de permitir que o sujeito visualize a figura-alvo enquanto está a tentar resolver o item (Bártolo-Ribeiro, 2003). O facto de esta prova ser realizada em contexto multimédia, através do uso de computador, por centenas de candidatos ao ano, faz dela um óptimo teste para estudar o comportamento psicométrico dos modelos logísticos da TRI.

Aproveitando uma base de dados disponível, pretendemos com o presente estudo testar os modelos de 1, 2 e 3 parâmetros logísticos na análise dos itens da prova “Padrões”, ilustrando assim a aplicabilidade que a Teoria de Resposta ao Item pode ter na validação e reestruturação das mais diversas provas.

MÉTODO

Amostra

A população em estudo é constituída por 1918 candidatos ao Curso de Pilotagem Aeronáutica da Academia da Força Aérea Portuguesa que prestaram provas entre 2004 e 2007. As idades dos candidatos oscilam entre os 17 e os 23, com uma média de idades de 18,7. Todos os participantes têm como mínimo de habilitações literárias o 12º ano de escolaridade completo, e 87,4% da amostra é do sexo masculino. Trata-se de uma amostra por conveniência (Maroco, 2007), que corresponde à totalidade dos candidatos que prestaram provas nos quatro anos consecutivos.

Instrumento

A prova “Padrões” é um teste de escolha múltipla informatizado, desenvolvido por Eugene Burke na década de noventa (Bártolo-Ribeiro, 2003), que avalia o constructo independência do campo. Semelhante ao teste das figuras embutidas, pode incorporar-se na classe dos testes de figuras ocultas, considerando que o participante tem que identificar se a figura-alvo – estímulo – se encontra em uma, nas duas, ou em nenhuma das figuras complexas apresentadas. A prova é composta por 10 itens, apresentados aos participantes numa sequência pré-estabelecida, sendo que para a resolução de cada um desses itens, os candidatos têm 1 minuto. A tarefa de resolução de cada item, tem presente a pressão temporal porque em janela própria, é apresentado em termos gráficos, o tempo restante em contagem decrescente. Essa barra, nos últimos dez segundos muda para a cor encarnada. Importante salientar que a pressão do tempo contribui para um aumento da ansiedade do candidato, podendo mesmo constituir-se como um factor não cognitivo limitador do sucesso da tarefa.

Na sua aplicação, solicita-se a cada um dos participantes que identifique uma figura-alvo em dois padrões visualmente desorganizados, sendo que a figura-alvo pode estar presente apenas num, nos dois ou em nenhum deles. O candidato deve escolher a sua resposta através de um teclado numérico premindo a tecla zero quando não encontra a figura-alvo em nenhuma das figuras complexas; a tecla um caso encontre a figura-alvo na figura complexa que se encontra no lado esquerdo; a tecla dois caso a figura-alvo esteja apenas na figura complexa do lado direito; e a tecla três caso se encontre em ambas.

Procedimento

A recolha de dados foi efectuada a posteriori, em 2007, através de uma rotina própria do sistema informático gestor da aplicação dos testes do Centro de Psicologia da Força Aérea Portuguesa. O teste Padrões faz parte da bateria de provas usada para o ingresso na Academia da Força Aérea Portuguesa, tendo sido aplicada em contexto real de selecção.

Em termos de análise estatística dos resultados, os itens foram analisados através do software BILOG-MG (Zimowski, Muraki, Mislevy, & Bock, 1996). Foram efectuadas várias execuções no sentido de se proceder à calibração dos itens e dos parâmetros de cada um dos três modelos. Foi também utilizado o Winsteps (Linacre & Wright, 2001), que é um software que permite a realização da análise dos dados, à luz do Modelo de Rash, ou Modelo Logístico de Um Parâmetro. Importa referir que o Winsteps (Linacre & Wright, 2001) faz a estimação dos parâmetros por máxima verossimilhança, ao passo que o BILOG-MG (Zimowski, Muraki, Mislevy, & Bock, 1996) utiliza processos de estimação bayesianos.

RESULTADOS

Antes de passarmos à verificação empírica dos modelos de 1, 2 e 3 parâmetros e apreciarmos o seu grau de adequabilidade face aos resultados empíricos obtidos nos itens do teste de dependência-independência de campo, quisemos proceder à verificação dos dois pressupostos prévios à aplicação da TRI: unidimensionalidade do teste e independência local dos itens.

Para a análise da dimensionalidade, procedemos à análise factorial das respostas aos itens. O teste KMO foi usado para verificarmos se os itens se encontravam suficientemente correlacionados (foi escolhido o KMO, em detrimento do teste de Bartlett, por este segundo ser sensível à dimensão da amostra). De acordo com Maroco (2007), o resultado da medida de adequação da amostragem obtido (KMO=0,69), é medíocre mas ainda aceitável, permitindo concluir que as variáveis se encontram suficientemente intercorrelacionadas.

Os resultados preliminares da referida análise factorial, sem imposição de limites ao número de factores a extrair, e de acordo com a regra de Kaiser, exibiram três componentes com valores próprios (eigenvalues) superiores a 1: o primeiro factor, com um valor-próprio de 1,99 explicava 20% da variância, o segundo factor com valor-próprio de 1,16 explicava 11% e o terceiro factor com valor-próprio de 1,04 explicava 10% da variância dos resultados nos 10 itens. Contudo, e embora a análise factorial sem forçar número de factores tenha sugerido a existência de 3 factores, a análise do Scree Plot evidenciou a possível existência de um factor muito forte, o que nos permitiu sustentar a justificação do pressuposto da unidimensionalidade da TRI para efeitos da prossecução deste estudo.

Avançando para a verificação do pressuposto da independência local, ou seja, a resposta dada a um item por um sujeito com determinado valor de θ, não é influenciada pelas respostas que deu a outros itens mas apenas reflecte o seu nível de traço (Andriola, 1998), tomámos a informação relativa à unidimensionalidade. Com efeito, o pressuposto da independência local pode derivar-se do princípio da unidimensionalidade, uma vez que os dois pressupostos são equivalentes (Hambleton et al., 1991). Assim sendo, e apenas para efeitos de prossecução deste estudo de ilustração, estão verificados os dois pressupostos base da TRI, pelo que poderemos passar à aplicação dos seus três modelos.

A Teoria de Resposta ao Item é uma metodologia muito valiosa na análise da qualidade dos itens de um dado teste, contudo, isto só se verifica quando os modelos se adequam aos dados empíricos, sem a evidência do ajuste do modelo, os resultados da análise podem ser suspeitos (Chernyshenko, Stark, Chan, Drasgow, & Williams, 2001; Pasquali, 2007). Como se pode verificar na Tabela 1, todos os valores dos índices Infit Mnsq e Oufit Mnsq oscilam entre 0,8 e 1,2, o que nos permite afirmar que os itens se ajustam ao modelo por serem considerados aceitáveis (cf. Linacre & Wright, 1994).

 

TABELA 1

Índices de ajuste do ML1 ao teste Padrões

 

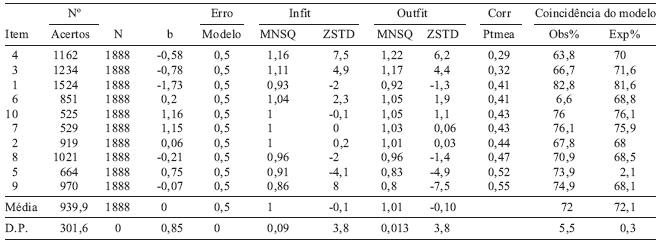
O Modelo de Rasch, permite-nos conhecer os valores do parâmetro b – dificuldade do item – revelando-se este valor através do nível de aptidão necessário para poder responder correctamente a cada um dos itens. Com base na análise do Winsteps (Linacre & Wright, 2001), podemos afirmar que o teste é fácil uma vez que, tendo em conta que o valor médio da aptidão é 0, os itens 1, 3, 4, 8 e 9, têm um parâmetro de dificuldade com valor negativo e o item 2 tem um valor de b muito próximo de zero (b=0,06), como se pode confirmar na Tabela 2. Através do mapa item pessoa podemos também afirmar que existe um número considerável de sujeitos com aptidões superiores às exigidas pelos itens mais difíceis.

 

TABELA 2

Amplitude das diferenças entre os parâmetros b obtidos através do ML1

 

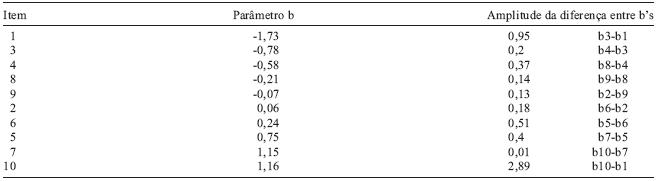
Como podemos verificar na Tabela 2 as amplitudes das diferenças entre os níveis de dificuldade dos itens são muito heterogéneas, sendo que os seus valores oscilam entre 0,01 (b₁₀-b₇) e 0,95 (b₃-b₁).

Um outro aspecto que nos parece relevante verificar, é se o grau de dificuldade de cada um dos itens está de alguma forma relacionado com o seu tipo de resposta. Recordemos que para cada um dos itens existem quatro tipos de resposta possíveis: (0) quando a figura-alvo não é encontrada em nenhuma das figuras complexas; (1) quando a figura-alvo se encontra na figura complexa do lado esquerdo; (2) quando a figura-alvo está no lado direito; e (3) quando a figura-alvo se encontra em ambas as figuras complexas. Depois de realizada essa análise, conseguiu-se fazer um match entre os três itens com menor grau de dificuldade, e o tipo de resposta 0. Contudo, não se consegue identificar um padrão claro entre os restantes tipos de resposta e o grau de dificuldade que os itens apresentam.

Em termos de adequação dos dados ao modelo de dois parâmetros (ML2), recorrendo-se para esta análise ao software BILOG-MG (Zimowski, Muraki, Mislevy, & Bock, 1996), a convergência foi verificada (maior mudança=0,001<0,01=critério de convergência). Inteirados de toda a panóplia de opiniões e divergências sobre a adequação dos modelos, tendo em conta que a única forma de obter as CCIs empírica e estimada através do software é forçar o procedimento estatístico com 10 itens, e sabendo que a alternativa é proceder ao desenho das curvas manualmente, optou-se por forçar o procedimento estatístico, solicitando ao software a criação das CCIs para todos os itens. De acordo com os outputs do software, o modelo ajusta-se apenas aos itens 3 e 4. Neste sentido, poder-se-ia concluir que o ML2 não é um modelo adequado à maioria dos itens que compõem o teste Padrões. Contudo, analisando o grau de ajuste de todos os itens através da análise gráfica da CCI teórica, e tendo em conta que o item 3 – considerado ajustado pelo próprio software – apresenta um ponto fora da margem de confiança e outro mesmo no seu limite, optou-se por considerar ajustados todos os itens que apresentassem até ao máximo de três pontos numa das duas condições supracitadas. Desta forma, consideram-se também ajustados os itens 1, 5 e 10.

Uma vez que o ML2 nos permite conhecer, além da dificuldade, a discriminação de cada um dos itens, podemos afirmar que os itens 3 e 4 apresentam um poder discriminativo muito baixo (0,18 e 0,14 respectivamente), os itens 1 e 10 apresentam um poder discriminativo baixo (0,43 e 0,43), e o item 5 tem um poder discriminativo moderado (0,88) (Baker, 2001). Os índices de dificuldade dos itens estimados pelo ML2 têm valores ligeiramente diferentes dos estimados pelo ML1, pois os processos de estimação utilizados pelos dois softwares são distintos, como já foi referido.

Não se prosseguiu com a verificação do ajuste do modelo ML3, por a convergência não ter sido alcançada para um critério de 0,005, quando forçado o procedimento estatístico para 10 itens.

DISCUSSÃO E CONCLUSÕES

O presente estudo propôs-se verificar qual dos três modelos para dados dicotómicos – ML1, ML2 e ML3 – se apresentava como o mais adequado aos itens que constituem o teste Padrões, com o fim último de salientar a aplicabilidade que a Teoria de Resposta ao Item pode ter na validação e identificação de pontos de melhoria, para uma eventual reestruturação da prova à luz da TRI.

Uma vez que a prova Padrões se apresenta como um teste de escolha múltipla, tornou-se particularmente relevante verificar o grau de acerto ao acaso, por parte dos participantes com baixa aptidão, nos itens que o compõem. Contudo, a análise anteriormente efectuada, permite-nos afirmar que o ML3 – modelo que permite ter conhecimento do parâmetro c – não se adequa de todo aos dados, uma vez que não chegou a ser cumprida a pré-condição, nomeadamente não se atingiu o critério de convergência. Algumas causas possíveis do desajuste são: (1) um parâmetro c com valor muito elevado; (2) a prova ser constituída por apenas dez itens, o que se apresentou como um obstáculo ao tratamento estatístico com o software BILOG-MG (Zimowski et al., 1996); (3) a baixa correlação total entre os itens, que por si só é já um mau prenúncio para o pré-requisito da unidimensionalidade; (4) a prova não ser unidimensional. A hipótese de falta de unidimensionalidade, no entanto, revela-se a mais provável uma vez que a análise factorial sem forçar número de factores, sugeriu a existência de 3 factores, e a correlação entre os itens é baixa.

No que diz respeito ao ML2 a pré-condição verificou-se, mas para se poderem obter as CCIs foi necessário forçar o software a computar a análise estatística do ajuste do modelo (pedindo as CCIs dos itens que, para um nível de significância de 0,005, não eram considerados ajustados). Essa análise revelou que os itens aos quais o modelo se ajustou, com critério de convergência de 0,005, foram os itens 3 e 4, sendo que através da metodologia gráfica para a análise do ajuste do modelo, se concluiu que os itens 1, 5 e 10 também se ajustavam ao ML2. Porém, os níveis de discriminação são baixos para todos os itens, à excepção do item 5 que detém, de acordo com Baker (2001), um moderado poder de discriminação.

Por um lado detemos o conhecimento de que nem todos os itens se ajustam ao modelo, mas por outro, vimos já que a TRI permite a realização de uma análise individual de cada item, sabemos que existem autores a defenderem a hipótese de itens de um mesmo teste serem ajustados a modelos diferentes (Embretson & Reise, 2000), e acrescentando a estes dois argumentos o facto de o ML2 nos dar mais informação do que o Modelo de Rasch, parece-nos que os itens acima mencionados deveriam ser representados através do ML2. É importante, no entanto, recordar que os itens são tanto melhores, para efeitos de avaliação psicométrica à luz da TRI, quanto maior o seu poder de discriminação, e neste caso concreto, verificámos que os itens que se ajustam ao ML2 não têm bom poder discriminativo.

O ML1, ou Modelo de Rasch, permite conhecer a dificuldade de cada um dos itens e é aquele que melhor se adequa aos dados, não se tendo verificado desajuste por parte de nenhum dos itens, através da análise dos resíduos estandardizados. O facto de se conseguir identificar um padrão entre os três itens com menor grau de dificuldade, e o tipo de resposta 0, sugere que os itens cuja figura alvo não se encontra em nenhuma das duas figuras complexas, são os mais fáceis.

Uma vez que existe ajuste do modelo a todos os itens, podemos avançar com algumas observações e sugestões para uma reformulação da prova. Tendo em conta que o item mais fácil apresenta um parâmetro de dificuldade de -1,73 e o mais difícil 1,16, a primeira observação que se pode fazer é o facto de espectro de dificuldade avaliado pelos itens ser grande (b₁₀-b₁=2,89). No ponto de vista da constituição da própria prova, embora seja constituída por cinco itens mais fáceis (leia-se com b<0) e cinco mais difíceis, tendo em conta o parâmetro b, constatou-se que a dificuldade dos itens não aumenta de forma gradual e equilibrada, verificando-se diferenças grandes no nível de exigência de um item para outro. Note-se que o item 1 é o mais fácil (b=-1,73), sendo que o segundo item mais fácil é o 3 (b=-0,78), havendo uma diferença de 0.95 nos seus graus de dificuldade.

A prova tem um item muito fácil (item 1), dois itens difíceis (itens 10 e 7), e os restantes têm valores intermédios de dificuldade, existindo itens que diferem no seu grau de dificuldade apenas por uma centésima, e outros que se distanciam por uma unidade. Neste sentido, e para que a prova seja mais eficiente, sugere-se que um dos itens mais difíceis (i₇ e i₁₀) seja retirado da prova, uma vez que têm os dois praticamente o mesmo nível de dificuldade (b₇=1,15, b₁₀=1,16). Se o ML2 se tivesse ajustado a estes dois itens, devia excluir-se o item que menos discriminação tivesse, como tal não se verificou, sendo que apenas o item 10 se ajusta ao ML2, sugere-se que seja retirado o item 7. Pode observar-se, também, que existe um número considerável de sujeitos cujas aptidões são superiores ao nível de aptidão necessário para responder ao item com maior parâmetro de dificuldade (b₁₀=1,16), neste sentido torna-se pertinente incluir na prova um item com um grau de dificuldade superior ao do item 10. Graves, Bezeau, Fogarty, e Blair (2004) adoptaram o mesmo procedimento no desenvolvimento de uma forma mais curta do Boston Naming Test (BNT), mas no sentido contrário, ou seja, como o teste era composto por muitos itens fáceis retiraram alguns deles.

O presente estudo permite-nos afirmar que a TRI, nos seus três modelos logísticos para dados dicotómicos, se apresentou como uma metodologia capaz de fornecer informação com bastante potencial para a análise e eventual reestruturação da prova “Padrões”.

 

REFERÊNCIAS

Andriola, W. (1998). Utilização da teoria de resposta ao item (TRI) para a organização de um banco de itens detinados a avaliação do raciocínio verbal. Psicologia, reflexão e crítica, 11, 1-13. Consultado em 4 Junho, 2008, de http://redalyc.uaemex.mx/redalyc/pdf/188/18811209.pdf        [ Links ]

Baker, F. B. (2001). The basics of item response theory. Washington, DC: ERIC.

Bártolo-Ribeiro, R. (2003). Os tempos de latência nas respostas aos itens de testes informatizados: Contributos para a compreensão do processamento cognitivo. Dissertação de mestrado não publicada. Instituto Superior de Psicologia Aplicada, Lisboa, Portugal.

Chernyshenko, O., Stark, S., Chan, K., Drasgow, F., & Williams, B. (2001). Fitting item response theory models to two personality inventories: Issues and insights. Multivariate Behavioral Research, 36(4), 523-562. Retrieved March 24, 2007 from the Psychology and Behavioral Sciences Collection database.

Embretson, S. E., & Reise, S. P. (2000). Item response theory for psychologists. New Jersey: Lawrence Erlbaum Associates, Inc.

Graves, R., Bezeau, S., Fogarty, J., & Blair, R. (2004). Boston naming test short forms: A comparison of previous forms with new item response theory based forms. Journal of Clinical and Experimental Neuropsychology, 26, 891-902. Retrieved September 5, 2008, from MEDLINE database.

Green, B., Bock, R., Humphreys, L., Linn, R., & Reckase, M. (1984). Technical guidelines for assessing computerized adaptive tests. Journal of Educational Measurement, 21, 347-360.

Guisande, M., Páramo, M., Tinajero, C., & Almeida, L. (2007). Field dependence-independence (FDI) cognitive style: An analysis of attentional functioning. Psicothema, 19, 572-577. Retrieved May 29, 2008, from PsycINFO database.

Hambleton, R., Swaminathan, H., & Rogers, J. (1991). Fundamentals of item response theory. New York: Sage publications.

Linacre, J. M., & Wright, B. D. (1994). Reasonable mean-square fir values. Rasch Measurement Transactions, 8, 370. Retrieved May 7, 2008 from http://www.rasch.org/rmt/rmt83b.htm.

Linacre, J. M., & Wright, B. D. (2001). Winsteps (Versão 3.61.1) [Computer software]. Chicago: Mesa Press.

Maroco, J. (2007). Análise estatística com utilização do SPSS (3ª ed.). Lisboa: Edições Sílabo.

Miyake, A., Witzki, A., & Emerson, M. (2001). Field dependence-independence from a working memory perspective: A dual-task investigation of the Hidden Figures Test. Memory, 9, 445-457. Retrieved May 20, 2008, doi:10.1080/0965821 0143000029.

Pasquali, L. (2007). Teoria de resposta ao item. Brasília, D.F.: Laboratório de Pesquisa em Avaliação e Medida.

Pasquali, L., & Primi, R. (2003). Fundamentos da Teoria de Resposta ao Item – TRI. Avaliação Psicológica, 2, 99-110. Consultado em Março, 10, 2008, através da fonte http://pepsic.bvs-psi. org.br/pdf/avp/v2n2/v2n2a02.pdf.

Wiberg, M. (2004). Classical test theory vs. Item response theory. Retrieved May 10, 2007, from http://www.umu.se/edmeas//publikationer/pdf/EMno50.pdf.

Yu, C. H. (2007). A simple guide to item response theory. Retrieved August 7, 2007 from http://www.creative-wisdom.com/computer/sas/IRT.pdf

Zimowski, M., Muraki, E., Mislevy, R., & Bock, R. (1996). BILOG-MG: Multiple-group IRT analysis and test maintenance for binary items (Versão 3.0) [Computer software]. Chicago: Scientific Software International (SSI).

 

^(*) Instituto Superior de Psicologia Aplicada, Lisboa.

^(**) Universidade do Minho, Braga.