Introduction
According to the Diagnostic and Statistical Manual of Mental Disorders (DSM-5; American Psychiatric Association [APA], 2013), the obsessive-compulsive disorder (OCD) is characterized by the presence of recurrent obsessions and/or compulsions that severely interfere with the daily functioning. Obsessions can be described as intruding thoughts, images or impulses that pervade the person’s stream of consciousness, without the subject being able to control them, while compulsions consist in repetitive behaviors, mental acts or rituals that the person feels compelled to perform, even if there is a desire to resist them. Compulsions may be performed in response to an obsession, like saying “magical” words to avoid certain things to happen, or they may consist in a set of rigidly performed actions, like washing and drying one’s hands exactly four times before leaving a washroom, or repeating six times a certain phrase to prevent a certain situation. In general, compulsions are usually intended to avert some feared event or to reduce distress, and most of the time they are not realistically connected with the things they try to prevent.
Measures
Several measures were developed to assess OCD, namely the Padua Inventory (PI; Sanavio, 1988) and its revisions, the Padua Inventory-Washington State University Revision (PI-WSUR; Burns et al., 1996) and the Padua Inventory-Revised (PI-R; Van Oppen et al., 1995), the Yale-Brown Obsessive-Compulsive Scale (Y-BOCS; Goodman et al., 1989) and the Y-BOCS-II; Storch et al., 2010), the Dimensional Obsessive-Compulsive Scale (DOCS; Abramowitz et al., 2010), the Vancouver Obsessive Compulsive Inventory (VOCI; Thordarson et al., 2004), the Inventory Obsessive-Compulsive - Revised (Rosa et al., 2005), the Schedule of Obsessions, Compulsions, and Pathological Impulses (SCOPI; Watson & Wu, 2005), the Obsessive-Compulsive Inventory (OCI; Foa et al., 1998) and the Obsessive-Compulsive Inventory Revised (OCI-R; Foa et al., 2002). Of the above, the Y-BOCS and Y-BOCS-II, which are clinician-rated instruments and mainly the OCI-R, a self-report instrument, are the most widely used (Angelakis et al., 2017; Hon et al., 2019; Koike et al., 2020; Overduin & Furnham, 2012; Wootton et al., 2015).
One commonly referred limitation of some of these measures is the fact that they often assess obsessions and compulsions separately, but several symptom dimensions include obsessions as well as compulsions (Anholt, 2010; Deacon & Abramowitz, 2005; Mataix-Cols et al., 2005). Another limitation of some of the above measures is the fact that their scores depend on the number and types of obsessive-compulsive (OC) symptoms, and this approach may not take symptom severity into appropriate account (Olatunji et al., 2017).
Several studies using factor analytic procedures have grouped OC symptoms into a small number of factors (Taylor et al., 2010), which include (a) checking compulsions, (b) washing rituals, (c) hoarding, (d) ordering and symmetry compulsions, (e) cognitive neutralizing rituals (i.e., mental acts of “undoing” the anticipated effects of a “bad” thought), and (f) obsessions characterized by aggressive, sexual, or religious themes (Foa et al., 2002; McKay et al., 2004). These six factors, apart from contributing to a total score, are assessed as individual dimensions in the OCI-R.
According to the Obsessive Compulsive Cognitions Working Group (OCCWG), normal and OCD individuals do not differ in the thoughts they have, but in the cognitive contents and processes, with the OC individuals evaluating the occurrence and content of their thoughts as personally important, highly unacceptable or immoral (Abramowitz et al., 2010). Therefore, the transition from normality to obsessive pathology is linked to the process that attaches dysfunctional appraisals or misinterpretations to the individual’s intrusive thoughts. Empirical research has shown that over 80% of non-clinical individuals reported the presence of intrusive thoughts, images or impulses in a similar manner of those with OCD, indicating that clinical conditions may be seen as an extreme variant of the above (Bouvard et al., 2017; Olatunji et al., 2008). In this scenario, the use of a cutoff score cannot be seen as a definitive threshold between OC and non-clinical groups. Also, the fact that most of the non-clinical individuals present in a mild form the symptoms of people with OCD, may be seen as an indicator in favor of a general factor, and thus a bifactor model, which could be present both in non-clinical and clinical groups.
In the original article the OCI-R was presented as a self-rating scale designed to assess the severity and type of symptoms of those potentially dealing with OCD (Foa et al., 2002), and a cutoff score of 21 was suggested to distinguish individuals with OCD from those without it, and the same value was recommended by others (Abramowitz & Deacon, 2006; Belloch et al., 2013; Kilicaslan et al., 2020), although different cut scores, ranging from 14 to 36 have been used in various populations (Abramowitz & Deacon, 2006; Gönner et al., 2008; Williams et al., 2013), but these discrepant values were probably due to heterogeneity of the samples used (Wootton et al., 2015). In our opinion, the use of a cutoff score, although necessary to distinguish NC and OC individuals, is limited in its interpretation, because of the continuous nature of these symptoms. In this perspective, anyone with 22 or more in the total score is classified in an OC group, but large differences exist in the range from 22 to 72, in terms of the symptom severity.
As mentioned above, the OCI-R is commonly used as the screening instrument for OCD in a large number of studies, which assess OCD symptoms and its relation with a wide variety of situations, namely alexithymia (Khosravani et al., 2017), epilepsy (Kilicaslan et al., 2020; Kim et al., 2020), suicidal experiences (Angelakis & Gooding, 2020), sexual functioning (Ghassemzadeh et al., 2017; Raisi et al., 2015), psychotic disorders (Schirmbeck et al., 2019), therapy outcome (Cludius et al., 2020; Külz et al., 2019; van Passel et al., 2016), neuropsychological performance (Winkworth & Thomas, 2019) or brain morphology and neurophysiological correlates of OCD (Hirose et al., 2017; Wagner et al., 2019; Wang et al., 2020; Yagi et al., 2017).
The bifactor model
In many situations, psychological instruments assess constructs that are comprised of a general factor and several related domains, which may be represented in one of two ways, through hierarchical models or bifactor models. Hierarchic or second-order models are used when specific lower-order factors are substantially correlated with each other, and a higher-order factor is hypothesized to account for the relationship among the lower-order factors (Mansolf & Reise, 2017).
Bifactor models can be used when there is a general factor that is hypothesized to account for the commonality of the items, as well as multiple domain specific factors, each of which is responsible for the unique influence of the specific domain over and above the general factor (Chen et al., 2006; Reise, 2012). The hierarchical and bifactor models differ essentially in the fact that in the hierarchical models, second-order factors explain the primary factors, which in turn explain item variation, while in the bifactor models, the general factor influences item variation directly, what means that in the bifactor models, the general factor and group factors compete equally to explain item variance and are set to be independent to each other (Chen et al., 2006; Mansolf & Reise, 2017). Thus, the bifactor model allows for the indicators to simultaneously load on an overall primary dimension and secondarily on distinct factors or domains, with specific factors modelling the residual association between the items once the contribution of the primary factor has been accounted for (Gibbons et al., 2007). The bifactor model provides an alternative to other non-hierarchical multidimensional representations of psychological concepts (Reise et al., 2007). In the typical specification of the bifactor model there are at least three indicators for each specific/group factor, which is the present case for the OCI-R, with one general factor and the six (uncorrelated) dimensions. Although the bifactor model may not be appropriate for all data and psychological phenomena, the bifactor model has been found to fit psychological data well across different problem areas, sample types, and ages (e.g., Ebesutani et al., 2014; Olatunji et al., 2019; Reise, 2012; Reise et al., 2007).
One notable advantage of the bifactor model is that it allows for easier interpretation and understanding of how specific content domains relate to external variables above and beyond the general factor. Therefore, the bifactor model may prove to be a useful approach to the OCD, since we can think of a structure with several dimensions being influenced by a general OC factor (Olatunji et al., 2017; Reise, Bonifay et al., 2013).
Although the bifactor model may be a valuable approach to better understand the structure of OC symptoms, no studies have examined the utility of this model in the OCI-R, with the vast majority of the studies so far mainly considering the six-factor correlated structure both in clinical (Abramowitz & Deacon, 2006; Belloch et al., 2013), non-clinical (Faria & Cardoso, 2017; Fullana et al., 2005; Hajcak et al., 2004; Malpica et al., 2009; Ólafsson et al., 2013; Roberts & Wilson, 2008; Zermatten et al., 2006) and both types of samples (Sica et al., 2009; Solem et al., 2010; Souza et al., 2011; Williams et al., 2013).
The present study aims to evaluate how the bifactor model fits the OCI-R, compared with three competing models - a general single factor model, a hierarchical second order model and the traditional correlated factors model.
Method
Participants
A total of 596 Portuguese adults participated in this study, 188 diagnosed with OCD and 408 without OCD from general population. In the OCD group (85 males, 103 females) ages ranged from 18 to 50 years old (M=33.8, SD=8.3), while in the non-clinical (NC) group (170 males and 238 females) ages ranged from 18 to 45 years old (M=32.5, SD=7.7). The clinical group was recruited in two private institutions and two central hospitals. Patients were diagnosed with OCD in accordance with DSM-V criteria in psychiatric consultation. Diagnosis times ranged from 4 months to 12 years, with a mean value of 2.5 years (SD=2.5). No differences were found for OCD and NC groups for age [t (594)=-1.78, n.s.], gender, educational level or marital status, p>.05 (see Table 1).
Measures
Participants answered a sociodemographic questionnaire, where information about age, gender, educational level and marital status were collected. For the clinical group, diagnosis time was also asked.
Obsessive-compulsive disorder was assessed by the Obsessive-Compulsive Inventory - Revised (OCI-R; Foa et al., 2002), an 18-item self-assessment questionnaire that evaluates the degree of disturbance regarding obsessive-compulsive symptoms during the last month. Responses are given on a five-point scale, from 0 (Not at all) to 4 (Extremely). The OCI-R includes six dimensions, (a) Hoarding, (b) Checking, (c) Ordering, (d) Neutralizing, (e) Washing, and (f) Obsessing, with three items each. The results for each subscale range from 0 to 12 and a total score is calculated by the sum of the 18 items, ranging from 0 to 72. The higher the total score on the scale, the higher the prevalence of symptoms.
The OCI-R showed good psychometric properties in several studies (Abramowitz & Deacon, 2006; Faria & Cardoso, 2017; Fullana et al., 2005; Malpica et al., 2009; Solem et al., 2010). In our study, the Portuguese version of the OCI-R (Faria & Cardoso, 2017) was used, which exhibited good convergent and divergent validity and Cronbach’s alpha values ranging from .61 to .90 for the six subscales and .89 for the 18-item scale (Faria & Cardoso, 2017).
Procedure
After approval of the ethical committee, clinical data were collected in four clinical institutions that specifically attend OCD patients, in two large Portuguese cities. Participants were assessed through a self-report protocol in an individual context, after their informed consent and explanation of all ethical issues. The whole protocol took about 15-20 min to complete (this study was part of a larger one, which also included the Beck Depression Inventory, the Beck Anxiety Inventory and the Yale-Brown Obsessive Compulsive Scale-II).
Data analytic approach
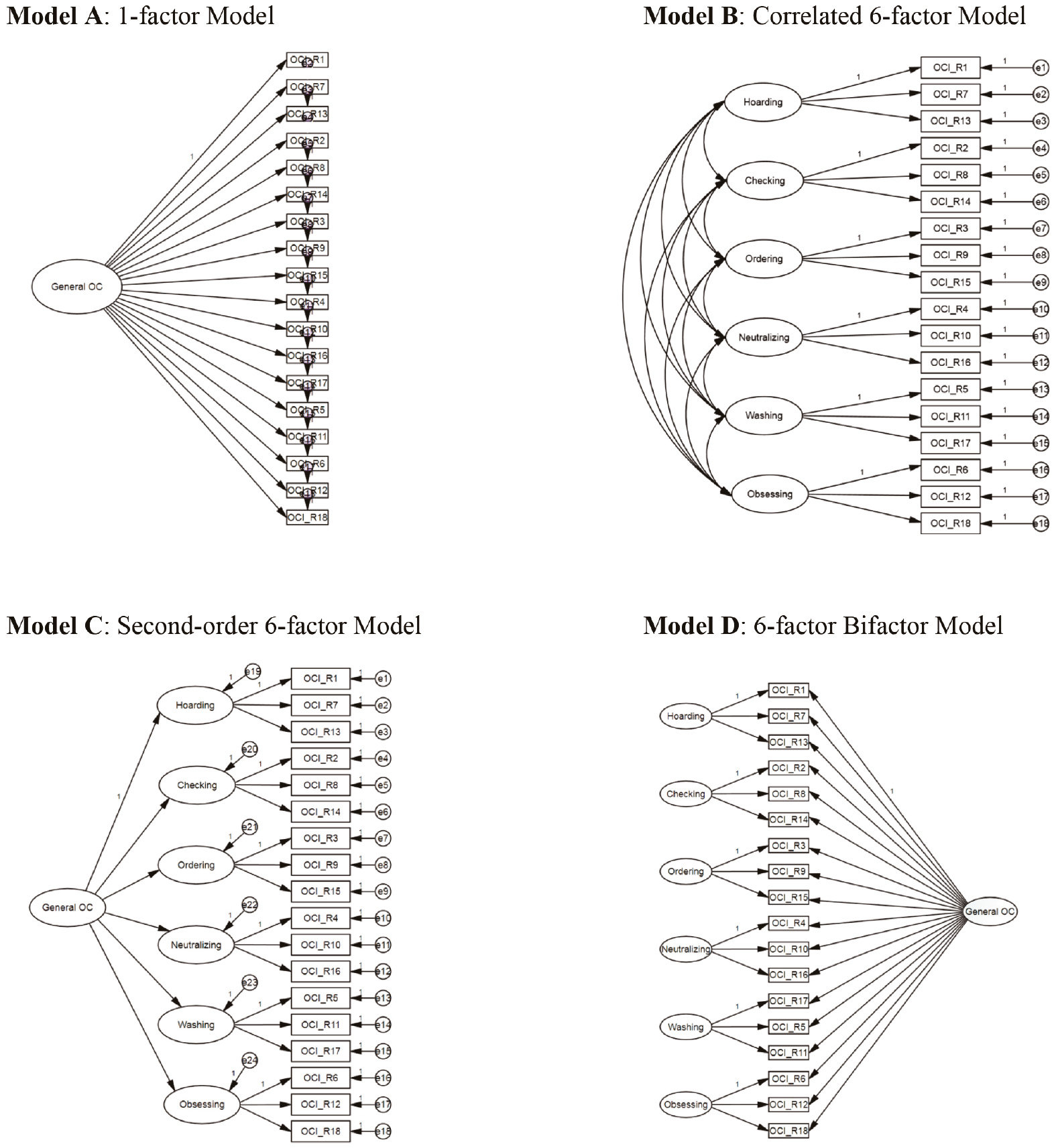
Confirmatory Factor Analyses. A confirmatory factor analysis (CFA) was conducted on the OCI-R using maximum likelihood method with robust estimators in EQS 6.3 (Bentler, 2006). Four models were tested (see Figure 1). The first (Model A) was a single-factor model with all items loading on one factor representing the general obsessive-compulsive dimension; the second (Model B), was a correlated 6-factor model (corresponding to the checking, ordering, neutralizing, washing and obsessing dimensions); the third (Model C), was a second order-model, where a general factor loads on the six dimensions and finally, a bi-factor model (Model D) with the six dimensions and a general factor loading in every single item.
To evaluate which model fits better the data, we used four approximate model fit indices and two information criteria, which make different assumptions and measure fit in different ways (Kline, 2015). The Comparative Fit Index (CFI; Bentler, 1990) and the Tucker-Lewis Index (TLI; Tucker & Lewis, 1973) were used because they reflect the improvement in fit relative to a baseline model, while the Standardized Root Mean Square Residual (sRMR; Jöreskog, 1978) and Root Mean Square Error of Approximation (RMSEA; Steiger, 1990) measure the absolute fit of the data to the model. Finally, the Akaike Information Criterion (AIC; Akaike, 1992) and the Bayesian Information Criterion (BIC; Neath & Cavanaugh, 2012) were used because they allow comparison of non-nested models. AIC is similar to the chi-square statistic, but it adjusts for the number of model parameters, thereby including a “penalty” function for model complexity. Similar to the AIC, BIC is another recommended fit statistic due to the importance it places on parsimony. Models can be compared with respect to the AIC and BIC values, and the model presenting the lower values is associated with a better model fit (Kline, 2015). The following recommended cut-points were used: CFI and TLI (≥.90, good, and ≥.95, desirable), RMSEA (≤.05, good fit; ≤.08, acceptable fit; ≥.10, poor fit) and sRMR (≤.06, good fit; ≤.08, acceptable fit) (Hu & Bentler, 1999).
Explained Common Variance and Percentage of Uncontaminated Correlations. The explained common variance (ECV) and percentage of uncontaminated correlations (PUC) are recommended indices that inform the consequences of forcing multidimensional data into a unidimensional structure when a particular set of data has a multidimensional structure that takes a bifactor form (Reise, Widaman et al., 2013).
The ECV statistic represents the percent of common variance attributable to the general factor (Reise, Widaman et al., 2013), and can be interpreted as the degree of “unidimensionality” when dealing with potential multidimensional data. High values of ECV (above .70) indicate that the general factor accounts for the majority of all common variance, whereas a low ECV means that item variance can be more accounted for by factors beyond the general factor (Reise, Widaman et al., 2013).
The PUC statistic indicates how much the factor strength will be biased due to forcing a bifactor structure into a unidimensional model (Reise, Widaman et al., 2013). With a bifactor structure, correlations among the items within group factors tend to be inflated due to both general factor and group factor variance, while correlations among items in different group factors only reflect variance from the general dimension and are thus uncontaminated by multidimensionality (Bonifay et al., 2015). As PUC increases, the average level of structural coefficient bias lessens, and a value above .80 is considered to represent negligible bias (Rodriguez et al., 2016).
Reliability. When we analyze multidimensionality and hierarchically structured constructs, the Cronbach’s α is misleading in how well a measure reflects a single construct (Cortina, 1993). As we apply bifactor structures, model-based reliability estimates should be computed that denote how precisely a certain scale score assesses the combination of general and specific constructs, and a certain target construct (Brunner et al., 2012).
Bifactor models offer the ability to use alternative statistics to better estimate reliability. Such statistics include the omega indices, which are “model-based” statistics based on confirmatory bifactor model results and are considered to be better able to yield more accurate estimates of reliability (Graham, 2006).
Omega. We computed Omega Total (which represents the reliability of the total score based on all sources of reliable variance across all the items) and Omega Subscale (which represents the reliability of a particular subscale based on all sources of reliable variance across the items from that subscale).
Omega Hierarchical. We also computed the omega hierarchical statistic (OmegaH; Zinbarg et al., 1997, 2005). a recommended statistic for evaluating the dimensionality of bifactor models, which can be applied to both the total score and subscale dimensions (Revelle & Zinbarg, 2009). The Omega hierarchical for the total score (OmegaH Total ) estimates the amount of total composite score variance explained by only the general dimension. This index reflects the degree to which the total score reflects a single latent construct. The Omega hierarchical for each subscale (OmegaH Subscale ) provides an estimate of subscale reliability, controlling for the general factor. As a consequence, Omega hierarchical statistics for the general factor are expected to be much higher than the Omega hierarchical statistics for each subscale.
Measurement Invariance analysis. We evaluated measurement invariance (MI) of the bifactor model across OCD and NC groups. First, we examined the fit of the single-group bifactor solutions in the OCD and NC samples separately. Next, we examined configural invariance across both groups, and if configural invariance was supported, then metric (weak) and scalar (strong) invariance were tested. Since our group sizes violated the assumption of equality (the NC group comprised around 70% of the sample), the assessment of both metric and scalar MI followed Chen’s (2007) recommendations. We used the ΔCFI test (difference between the CFI values of both models) because it has been recommended over the χ 2 difference test and the ΔRMSEA and ΔsRMR test, since it is not influenced by sample size or model complexity (Chen, 2007).
Results
Confirmatory Factor Analyses
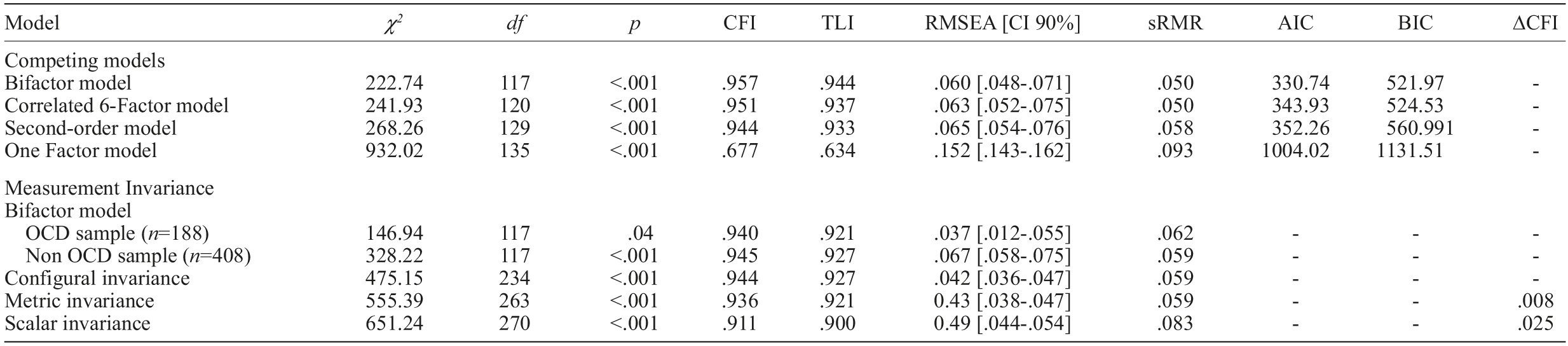
Results of the goodness-of-fit indexes are shown in Table 2. The 1-factor model inadequately fit the data, considering the criteria proposed for the fit indices (Hooper et al., 2008; Hu & Bentler, 1999).
Table 2 Fit statistics for the confirmatory factor analytic models
Note. χ 2 =Satorra-Bentler scaled chi-square; df=degrees of freedom; CFI=Comparative fit index; TLI=Tucker-Lewis index; RMSEA=root mean square error of approximation; sRMR=standardized root-mean-square residual; AIC=Akaike information Criterion; BIC=Bayesian information criterion; DCFI=change in CFI.
Evidence obtained in our study demonstrated that models with six factors showed a significant improvement of the fit indices, particularly the bifactor model, with six dimensions and a general factor, which presented the best fit of all models tested, with a value of Satorra-Bentler’s χ 2 =222.74, df=117, p<.001, χ 2 /df=1.903, CFI=.957, TLI=.944, RMSEA=.060, sRMR=.050, and regarding comparative values, AIC=330.74 and BIC=521.97, the lowest of the four models tested.
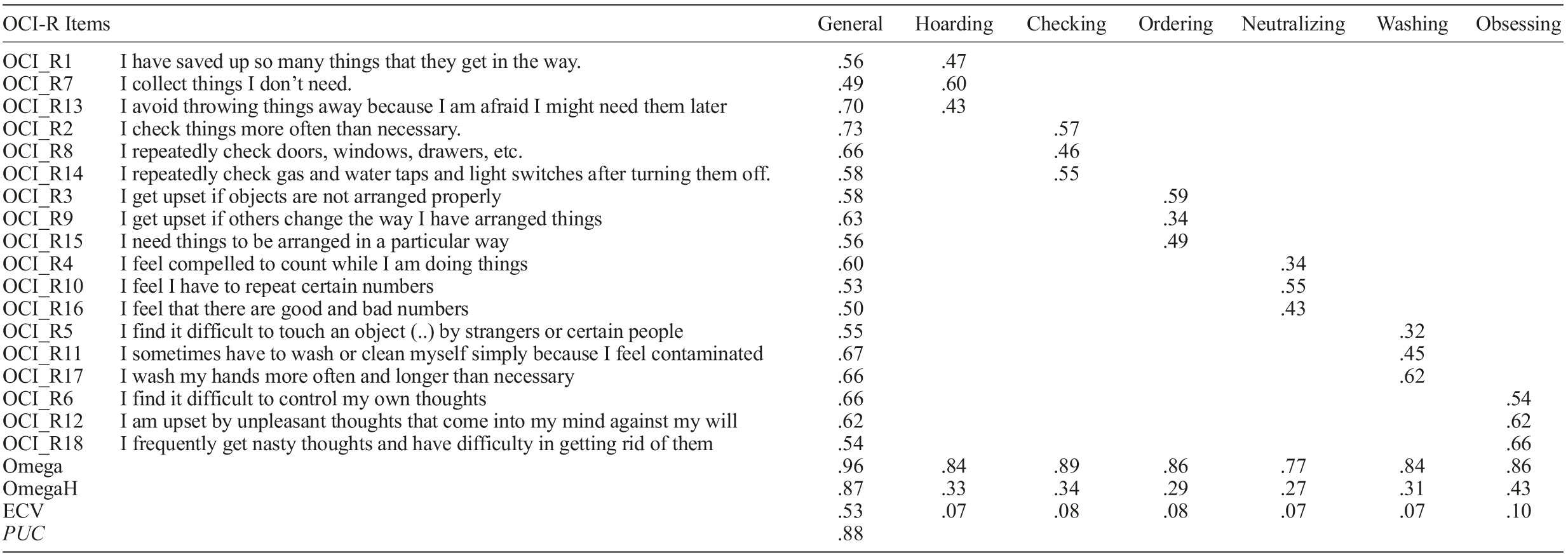
The bifactor model differentiates significantly from the model with the second best fit (χ 2 (3)=19.19, p<.001), using the chi-square change criterion (Hooper et al., 2008; Hu & Bentler, 1999). All items also loaded significantly on the general OC factor (with loadings ranging from .49 to .73) as well as on each of the six domains, ranging from .32 to .66 (see Table 3 for all factor loadings).
Explained Common Variance and Percentage of Uncontaminated Correlations
In our study, the ECV statistic associated with the confirmatory bifactor model presented a value of .53, indicating similar importance of both the general and particular factors. The value of the PUC statistic associated with the confirmatory bifactor model was .88, which suggests that fitting OCI-R items into a unidimensional structure (the bifactor model with a general factor) will not introduce a significant degree of bias on structural coefficients.
Reliability
In Table 3 are represented the reliability statistics for the total score and the six dimensions. The Omega General for the total score had a value of .96, indicating high reliability, while the Omega Subscale values for the six dimensions were .84 (Hoarding) .89 (Checking), .86 (Ordering), .77 (Neutralizing), .84 (Washing) and .86 (Obsessing).
The value of the OmegaH Total was high, .87, supporting the presence of a strong general OC dimension, while the values of the OmegaH Subscales , aried from .27 (Neutralizing) to .43 (Obsessing). These values were naturally lower since they represent the reliability of the subscales after accounting for the reliability due to the general factor.
Measurement Invariance Analysis
Two separate CFA’s were conducted, one for the OCD group [χ 2 (117)=146.94, p=.04; CFI=.940; TLI=.921; RMSEA=.037; sRMR=.062], and the other for the NC group [χ 2 (117)=328.22, p<.001; CFI=.945; TLI=.927; RMSEA=.067; sRMR=.059]. Since the results indicated an adequate fit for both samples, we then tested for MI. Configural invariance in OCD and NC groups was supported, with good fit values [χ 2 (234)=475.15, p<.01; CFI=.944; TLI=.927; RMSEA=.042; sRMR=.059]. Metric invariance was also supported, with adequate fit values (see Table 2) and a value of ΔCFI (0.008) below the recommended threshold of 0.01. We finally tested for scalar invariance, but although the fit indices were within the boundaries of acceptable fit (see Table 3), the change in CFI (0.046) was well above the recommended value of .01, so scalar invariance was not supported.
Discussion
Although the vast majority of studies in which the OCI-R was used consider a correlated six- factor structure (e.g., Abramowitz & Deacon, 2006; Faria & Cardoso, 2017; Olafsson et al., 2013; Solem et al., 2010), the present study examined the bifactor structure of the OCI-R, which was tested against three other models, a single factor model, a correlated six-factor model and a second order model with a general factor loading on the six domains.
Our results showed that the single factor model presented a very poor fit, with all the indices well below the acceptable values. On the other hand, although the correlated six factor model and the hierarchical second order model presented good fit values, the bifactor model was the one with the better fit, what supports the presence of a bifactor model for the OCI-R, with both the six dimensions and general factor loading on the items of the scale.
The present study also found that the general OC factor and the six specific OC symptom dimensions showed good reliability, estimated by the Omega indices since they generally provide better estimates than coefficient alpha (Dunn et al., 2014; Peters, 2014), and because they evaluate adequately the reliability of the specific OC symptom dimensions as well as the reliability attributed to the general OC factor.
The OmegaH Total for the general factor, corresponding to the amount of total score variance associated with variation on the general OC factor common to all the items was high (.80), thus suggesting the presence of a strong and reliable general factor, while the OmegaH Subscale for each of the six dimensions, corresponding to the degree to which the six specific OCI-R dimension scores provide reliable variance after accounting for the general OC factor were lower, as expected under the condition of a valid general factor. Also, the OmegaH Subscale values being similar, indicate that the six dimensions have the same importance.
With regard to dimensionality, the ECV value (.53) evidentiates a general factor responsible for about a half of the total variance, suggesting that some multidimensionality exists, while the value of PUC (.86) is above the threshold of .80 (Rodriguez et al., 2016), therefore no significant bias is introduced by considering a bifactor structure.
Regarding measurement invariance, our results showed that configural and metric invariance were supported across clinical and NC groups, while scalar invariance was not. This invariance of the bifactor model shows that this structure of a general factor and six dimensions is adequate for both clinical and non-clinical groups, suggesting that the symptom structure is similar in those with and without OCD, as noted earlier by Olatunji et al. (2017).
The use of the OCI-R allows for the differentiation of clinical and non-clinical individuals, by means of a cutoff score. In our view, this is a somewhat limited approach, since the conceptualization of the OC symptomatology as a continuum (Bouvard et al., 2017; Olatunji et al., 2008), does not allow for a clear distinction between the two realities. For instance, individuals with a total score of 19 or 20 are considered as non-clinic, while in fact they present more similarities with other individuals just above the cutoff limit (e.g., with 22 or 23) than with others, non-clinic, with a score of 10 or 12. It is necessary to introduce different levels of symptom severity in the OCD group, for instance mild, moderate and severe (see Abramovitch et al., 2010), and perform ROC analyses for each of these levels, in order to determine the optimal levels in terms of sensitivity and specificity. This study has several limitations. First, OCD group presents a wide variability in diagnosis times, from 4 months to 12 years, which turns our clinical group into a heterogeneous one, mostly in terms of symptom severity and treatment and medication time, and it is known that the OCI-R is sensitive to the effects of treatment in adults (Taylor et al., in press). Another limitation is the lack of control of comorbidities, since it is known that OCD is associated with several clinical conditions (Angelakis & Gooding, 2020; Brakoulias et al., 2017; Winkworth & Thomas, 2019). Also, because of the large span in diagnosis times, some patients were still diagnosed according to the DSM-IV criteria and others, with more recent diagnosis times, were done so according to the DSM-5 criteria, and it is possible that our OCD group included some individuals with hoarding symptomatology, diagnosed under the DSM-IV criteria. Also, diagnosis of compulsions or obsessions in DSM-5 require that they are time-consuming (more than one hour per day) and responsible for significant distress or impairment in functional areas, and these data were not available.
In conclusion, the bifactor model is adequate for the OCI-R, and in spite of the heterogeneity of OC symptoms, it exhibited good fit in both clinical and non-clinical samples. This model allows for the communalities due to a general OC factor along with the separate dimensions, in individuals with or without an OCD diagnosis. One of the advantages of the bifactorial models is the fact that the variation explained by specific factors or dimensions is independent of the general factor, what does not happen in the other models tested, and this allows a better understanding of how the specific dimensions correlate with external variables, in addition to the general factor. In addition, the bifactorial models also make possible the evaluation to what extent the variation in responses is due to a general construct or to the different dimensions.
We also think that the bifactor structure is compatible with other classifications of the OC symptoms, obtained through latent class analysis, namely those of autogenous vs. reactive obsessions (Lee et al., 2005), or the more recent proposed classification of autogenous obsessive, reactive obsessive-compulsive and reactive compulsive (Atli et al., 2014), because these classes are not mutually exclusive, therefore allowing for the presence of a common factor.