Evaluación de la vulnerabilidad a la degradación por erosión en suelos mediante un modelo de lógica borrosa

 

I. Melendez-Pastor ¹, P. Córdoba Sola, J. Navarro-Pedreño & I. Gómez

¹ Grupo de Edafología Ambiental, Departamento de Agroquímica y Medio Ambiente. Universidad Miguel Hernández de Elche. Av. de la Universidad s/n. Edificio Alcudia. 03202 Elche (España). E-mail: imelendez@umh.es / jonavar@umh.es, Tfno. +34 966658417, Fax: +34 966658340

 

RESUMEN

Se presenta un modelo simplificado para evaluar la vulnerabilidad de suelos a proce­sos degradativos, tales como la erosión. Es­tá basado en el empleo de la lógica borrosa para operar con variables predictivas con­tinuas estimadas a partir de imágenes de te­ledetección y modelos digitales de eleva­ciones. Combina variables explicativas re­lativas al estado de la cubierta vegetal y di-versos parámetros topográficos. Las esti­maciones se realizan mediante un sistema de decisión implementado en un sistema de información geográfica (SIG), obteniéndo­se mapas de vulnerabilidad que pueden ser actualizados con nuevas imágenes de saté­lite. La zona estudiada se localiza en el su­reste peninsular, caracterizado por un clima Mediterráneo semiárido. Se estimaron altas tasas de vulnerabilidad para todas las esti­maciones realizadas, en relación a los um­brales máximos y mínimos esperables. Se estudio la respuesta de los cambios de vul­nerabilidad en relación a los cambios de clases de erosión actual a potencial según el modelo USLE. Se estimó una alta corre­lación entre los cambios de clases de ero sión y los cambios de estimaciones de vul­nerabilidad.

Palabras claves: Vulnerabilidad de suelos, lógica borrosa, SIG, teledetección.

 

Assessment of soil vulnerability to erosion by a fuzzy logic model

ABSTRACT

A simplified fuzzy logic model to assess soil vulnerability to degradation processes, such as soil erosion, is presented. The model is based on the use of fuzzy logic to operate with explanatory continuous variables esti­mated from remote sensing images and digi­tal elevation models. It combines explana­tory variables concerning the state of vege­tation cover and topographic parameters. The estimations are made by a decision sys­tem implemented in a geographic informa­tion system (GIS). Output vulnerability maps can be updated with new satellite im­ages. The study area is located on the south­east Iberian Peninsula, characterized by a semiarid Mediterranean climate. It was found high vulnerability for all estimations in relation to the expected maximum and minimum thresholds. Responses of the vulnerability changes in relation with changes of existing classes of potential erosion (based on the USLE) were analysed. It was considered a high correlation between changes in classes of soil erosion and changes in vulnerability estimations.

Key-words: Soil vulnerability, fuzzy logic, GIS, remote sensing.

 

INTRODUCCIÓN

La degradación del suelo es un proceso biofísico originado por diferentes causas so­cioeconómicas y políticas que inducen una disminución de su calidad o reducción de su productividad (Eswara et al., 2001). La de­gradación del suelo implica la pérdida de la capacidad del sistema edáfico para desarro­llar sus funciones (Poch & Martínez Casasnovas, 2006). Un concepto relaciona­do con la degradación del suelo es la vulne­rabilidad del suelo. Este último se refiere a la sensibilidad de un suelo frente a los pro­cesos degradativos. La vulnerabilidad del suelo es la capacidad de que una o varias de las funciones ecológicas del suelo sean mermadas (Blum, 1990) La vulnerabilidad de un suelo se relaciona con la sensibilidad que posee frente a los procesos degradativos del mismo (erosión, desertificación, salini­zación,...), ejerciendo un papel crucial facto-res tales como la vegetación y la topografía del terreno. Suelos con una baja cobertura vegetal y elevadas pendientes resultan más vulnerables.

La erosión del suelo es una de tipos más notables de degradación edáfica, estando originada por la remoción activa de partícu­las debido a las fuerzas gravitacionales, el flujo de agua o del viento (Kapur & Akça, 2006). La importancia de la erosión del suelo en la degradación edáfica y la desertifica­ción en el ámbito mediterráneo está plena­mente reconocida (Brandt & Thornes, 1996). En el caso particular del sureste pe­ninsular, la conjunción de factores tales co­mo la existencia de un clima mediterráneo semiárido, altas tasas de pérdida de suelo por erosión o la elevada recurrencia de in­cendios, la hacen particularmente suscepti­ble de sufrir procesos de desertificación (MARM, 2008).

Los Sistemas de Información Geográfica (SIG o GIS por sus siglas en inglés) han si­do frecuentemente utilizados para la mode­lización de procesos de degradación edáfica (Lu et al., 2004; De Paz et al., 2006; Conta­dor et al., 2009). Dada la complejidad in­trínseca del sistema edáfico, los modelos en ciencias del suelo suelen estar caracterizado por la existencia de múltiple y a veces con­flictivos atributos, e incertidumbres en la concepción de las preferencias y los datos (McBratney & Odeh, 1997). Es por ello que se han desarrollado sistemas basados en la lógica borrosa (fuzzy logic) para representar la incertidumbre en las variables de predic­ción y en los atributos o clases predichas (McBratney et al., 2003). A raíz de esta po­tencialidad de la lógica borrosa en la mode­lización de procesos edáficos, numerosas aplicaciones se han desarrollado en el ámbi­to de la modelización de la degradación edá­fica (Tran et al., 2002; Metternicht & Gon­zalez, 2005; Cohen et al., 2008). En torno a esta línea, Melendez-Pastor et al. (2006) proponen un modelo experimental basado en la lógica borrosa para evaluar la vulnera­bilidad de los suelos a su degradación. Se basa en el empleo de imágenes de satélite y modelos digitales de elevaciones, para eva­luar el efecto de la cobertura vegetal y la to­pografía en la vulnerabilidad a la degrada­ción por erosión.

El objetivo de este estudio es aplicar un modelo empírico experimental para la eva­luación de la vulnerabilidad de los suelos a un área de estudio del sureste peninsular, y analizar la relación existente entre los in­crementos de las estimaciones de vulnerabi­lidad, respecto a los cambios en las tasas de erosión actual a potencial según el modelo RUSLE.

 

MATERIALES Y MÉTODOS

El área de estudio (Figura 1) está ubicada en el sureste peninsular, concretamente en la sierra de Escalona (provincia de Alicante).

 

Figura 1. Localización y Modelo Digital de Elevaciones (DEM) del área de estudio.

 

Se trata de un área con clima semiárido de acuerdo con el índice de aridez de la UNEP (1997). Según el sistema de clasificación climática de Köppen, es de clase Bsk que se corresponde con áreas de clima seco con una estación estival seca y temperaturas medias anuales inferiores a los 18ºC). Las principales tipos de suelos son Calciorthid, Torriorthent y Camborthid (IGN-CNIG, 2005). Los principales usos del suelo son los cultivos intensivos de regadío, mezclados con pinares y zonas de matorrales xerófitos.

En este estudio se aplicó un modelo de lógica borrosa para la estimación de la vul­nerabilidad de los suelos. La lógica borrosa (Fuzzy logic) surge a raíz de la Teoría de Conjuntos Borrosos (Fuzzy Sets en inglés) desarrollada por Zadeh (1965), que definió el concepto de los conjunto borroso como: un conjunto borroso A en X es caracterizado por una función de pertenencia (members­hip function) fA(x) que asocia cada punto en X un número real en el intervalo [0,1], en el que el valor de fA(x) en x representando el grado de pertenencia de x en A; cuanto más se aproxima el valor de fA(x) a la unidad, mayor es el grado de pertenencia de x en A. La lógica borrosa tiene la enorme potencia­lidad de trabajar con variables continuas ta­les como mapas de parámetros edáficos, pa­ra las que se define una determinada función de pertenencia según su comportamiento observado con respecto al fenómeno de es­tudio. La teoría de los conjuntos borrosos aportar una interesante herramienta mate­mática para comprender problemas de deci­sión y para construir reglas de decisión en sistemas de evaluación multi-criterio (East­man, 2009).

La vegetación, el relieve y los tipos de suelos están considerados entre los factores más influyentes en el comportamiento de los suelos frente a los procesos erosivos (Morgan, 1997). Es por ello que han sido considerados en el modelo aquí presentado. Dado que existe una cierta homogeneidad en cuanto al tipo de suelos a nivel de la es­cala de trabajo utilizada (el área de estudio se corresponde con una unidad ambiental cartografía previamente por Antolín (1998), con una litología y erosividad homogéneas para la superficie analizada), el parámetro tipo de suelo se consideró homogéneo para toda el área de estudio por lo que no fue in­cluido en posteriores fases de la modeliza­ción. Es por ello que el modelo, combina de manera simplificada dos tipos de informa­ción para evaluar es estado de la degrada­ción del suelo, siendo estos la topografía (que a su vez considera la pendiente y orien­tación de las laderas) y el estado de la cu­bierta vegetal. La topografía determina en gran medida la formación del suelo (Jenny, 1941) y la erosión hídrica del suelo (Wischmeier & Smith, 1965). Las pérdidas de suelo se incrementan exponencialmente conforme se incrementa la pendiente Wischmeier & Smith, 1965), mientras que la orientación de las laderas posee un efecto diferencial en las tasas de erosión (Agassi & Ben-Hur 1991) siendo las laderas orientadas al sur las más vulnerables. Por otra parte, la vegetación tiene una influencia directa e in­directa en los procesos erosivos mediante los siguientes mecanismos (Box & Bruce, 1995; Torri & Borselli, 2000): 1) las hojas y ramas, muy especialmente las hojas y ra­mas muertas de la superficie del suelo, in­terceptan parte de las gotas de lluvia redu­ciendo su energía cinética; 2) al disminuir la energía del impacto, se favorecen altas tasas de infiltración mediante la reducción del se­llado superficial; 3) la vegetación incremen­ta la resistencia hidráulica reduciendo la ve­locidad de la escorrentía; 4) reduce los mo­vimiento de tierras por el anclaje que pro­porciona el sistema radical; y 5) proporciona materia orgánica al suelo incrementando la estabilidad de los agregados. El modelo em-plea la capacidad de la lógica borrosa para modelizar el comportamiento de las varia­bles explicativas de un modo más realista que con un modelo de lógica booleana.

En la Figura 2 se muestra un diagrama de flujo simplificado del modelo de lógica bo­rrosa empleado. Las variables explicativas de vulnerabilidad seleccionadas representan el estado de la cubierta vegetal (variable NDVI) y la topografía del terreno (variables pendiente y orientación). La variable NDVI se obtiene a partir del calculó mediante imágenes de teledetección del índice espec­tral NDVI (Normalized Difference Vegeta­tion Index), cuya formulación original se atribuye a Rouse et al. (1974), siendo éste el ratio normalizado entre la reflectividad de cubiertas en el infrarrojo cercano y el rojo. El NDVI ha sido relacionado con múltiples parámetros relativos al estado de la vegeta­ción, tales como la cantidad de biomasa, el contenido en clorofila, el contenido hídrico d ellas hojas, el índice de área foliar (o leaf area index LAI en inglés) y otros muchos (Chuvieco, 2002). Por su parte, las variables topográficas se obtienen a partir de un mo­delo digital de elevaciones (MDE o Digital Elevation Model DEM en inglés). Los MDE pueden obtenerse de múltiples maneras, siendo lo más habitual el utilizar mapas to­pográficos tradicionales, o mediante senso­res aerotransportados (e.g. LIDAR) o senso­res satelitales (e.g. RADAR, sensores ópti­cos multi-angulares). A cada variable intro­ducida en el modelo se le asignó una fun­ción de pertenencia dependiendo su com­portamiento en relación al proceso de ero­sión y los rangos de valores para los que de­seaba fuese modelizada. Las funciones de pertenencia se caracterizaron según dos pa­rámetros (Eastman, 2009): 1) el tipo de función, pudiendo ser sigmoidea, exponencial (J-shaped), lineal o definida por el usuario; y 2) el comportamiento de la función, pudiendo ser monotónicamente creciente, monotónicamente decreciente o simétrica. Es esperable que suelos con baja cobertura vegetal y pendientes muy abruptas orienta das al medio día sean más vulnerables frente a la erosión. El modelo propuesto emplea las siguientes funciones de pertenencia para las variables de entrada: 1) NDVI, función linear monotónicamente decreciente; 2) pendiente, función exponencial monotónicamente creciente; y 3) orientación, función linear simétrica. Finalmente, las funciones de pertenencia son combinadas ponderando su importancia relativa para obtener la estimación final de vulnerabilidad.

 

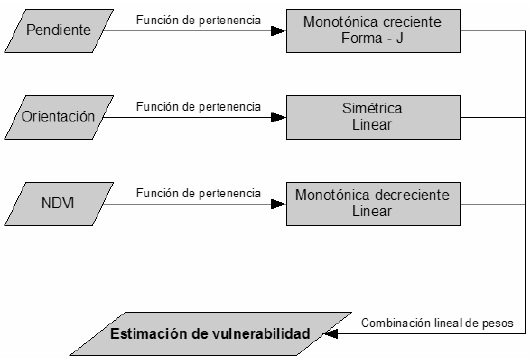
Figura 2. Diagrama de flujo del modelo de lógica borrosa

 

El modelo digital de elevaciones se generó a partir de cartografía vectorial (escala 1:10.000) que, mediante la estimación de polígonos TIN (Triangulated Irregular Network), se realizó una interpolación para ob­tener un MDE ráster con resolución espacial de 15m. Las variables pendiente y orienta­ción de laderas se calcularon a partir del MDE obtenido. En la Figura 1 se muestra el MDE empleado en el modelo.

Para la estimación de la variable relativa a la cobertura vegetal, se utilizaron cuatro imágenes multiespectrales adquiridas por el sensor ASTER, abordo del satélite TERRA. Las imágenes fueron adquiridas coincidien­do con el final de la primavera y final de ve­rano, para los años 2000 (30 junio y 1 de agosto) y 2003 (22 mayo y 10 de agosto). La selección de tales fechas se debe a que a finales de verano la vegetación está comple­tamente seca debido a la práctica ausencia de precipitación, y presenta un grado menor de protección del suelo respecto a la prima­vera. Las imágenes estaban corregidas at­mosféricamente, presentando reflectividad en superficie (producto de nivel 2 AST_07) con una resolución espacial de 15m.

El modelo de lógica borrosa se desarrolló en el software IDRISI Andes, realizándose una estimación de vulnerabilidad para cada una de las imágenes de satélite, con la fina­lidad de evaluar las variaciones estacionales (primavera, final del verano) e inter-anuales (2000, 2003). Estas cuatro estimaciones o escenarios, se corresponden con las fechas de adquisición de las escenas del sensor ASTER tal y como se presentan en la tabla 1.

 

Tabla 1. Relación de estimaciones de vulnerabilidad realizadas y escenas ASTER utilizadas.

 

En base a las estimaciones de vulnerabili­dad derivadas del modelo, se evaluó el por­centaje de cambio experimentado compa­rando todas las estimaciones. Adicional­mente se utilizaron a fines de establecer un rango de posibles valores de vulnerabilidad para el área de estudio, una estimación del máximo valor posible del índice de vegeta­ción (NDVI=1) y un valor del índice de ve­getación crítico para cubiertas desnudas (NDVI=0,1) (Holben, 1986).

Con la finalidad de evaluar el funciona­miento del modelo de vulnerabilidad con re­lación a la erosión de suelos, se utilizaron con fines comparativos mapas de erosión actual y potencial (Figura 3a y b) estimados mediante la aplicación del modelo USLE adaptado a la Comunidad Valenciana (An­tolín, 1998). Incrementos en las tasas de erosión (de una determinada categoría de erosión actual a otra diferente de erosión po­tencial) se identificaron con 1 y “no cam­bios” con 0. De este modo se pudieron cal­cular modelos de regresión logística bino­mial entre los incrementos de erosión (va­riable dependiente booleana), respecto los resultados de los cambios de vulnerabilidad.

 

Figura 3. Mapas de erosión actual (a) y erosión potencial (b) para el área de estudio en base al mode-lo RUSLE. Fuente de datos: Antolín (1998).

 

RESULTADOS Y DISCUSIÓN

Las estimaciones del índice espectral NDVI (Figura 4) muestran altos valores (mayor cantidad de vegetación) para las áreas de cultivo (zonas de forma poligonal y valores homogéneos) y vaguadas húmedas en los barrancos. Así mismo se puede apreciar una cierta variabilidad estacional con mayores valores para las imágenes de primavera. Es­tos mayores valores en primavera se deben al régimen ombrométrico del área de estu­dio, donde las mayores precipitaciones son en primavera y otoño, mientras que una acusada sequía estival propicia la disminu­ción de la vigorosidad de la vegetación y consecuentemente, una disminución en los valores del NDVI.

 

Figura 4. Estimaciones del índice de vegetación NDVI para: a) primavera 2000, b) verano 2000, c) primavera 2003, y d) verano 2003.

 

Se obtuvieron valores altos de vulnerabi­lidad para el área de estudio en todas las es­cenas, debido a la abrupta orografía existen­te y la poca vigorosidad de la cobertura ve­getal. En la Figura 5 se puede observar có­mo se obtuvieron valores promedios de vul­nerabilidad >80% para la todas las escenas en base a las que se aplicó el modelo. No se aprecia un cambio significativo entre la estimación de vulnerabilidad en la escena E01 y E02, mientras que sí que es posible apreciar un cambio más notable entre las escenas E31 y E32, debido a una disminución de la cobertura vegetal. En la Figura 7 pueden observarse las estimaciones del modelo de vulnerabilidad para las escenas E31 y E32.

 

Figura 5. Estimaciones del vulnerabilidad del suelo para: a) primavera 2000, b) verano 2000, c) pri­mavera 2003, y d) verano 2003.

 

Es posible apreciar un notable aumento en la estimación de vulnerabilidad en el centro de la escena (cambio de verde a marrón), atribuible a la eliminación de la co­bertura vegetal en parcelas agrícolas.

Los mejores resultados de los modelos de regresión logística se obtuvieron me­diante la inclusión de las variables inde­pendientes por el método de pasos hacia atrás por razón de verosimilitud. La de­tección de los incrementos de vulnerabili­dad a la erosión, fue muy alta, ya que se alcanzó un porcentaje de acierto global del 82,3% utilizando como variable inde­pendiente los porcentajes de cambio de vulnerabilidad. La detección de “no in­crementos” de vulnerabilidad a la erosión fue muy baja, debido a que las variables independientes utilizadas en los modelos estaban calculadas para estimar cambios de vulnerabilidad detectados mediante el modelo de lógica borrosa.

 

CONCLUSIONES

El empleo del modelo de estimación de vulnerabilidad mediante lógica borrosa se muestra altamente eficiente para la detec­ción de incrementos en la vulnerabilidad a la erosión de suelos, pudiendo realizarse de manera sistemática y con alta frecuen­cia temporal estimaciones de vulnerabili­dad, que permitirían un seguimiento tem­poral.

El modelo aquí presentado es un mode-lo simplificado, que brinda un marco de desarrollo marcado por el empleo de la lógica borrosa e información derivada de imágenes satelitales, cuya mejora y cali­bración presenta indudables oportunida­des para el desarrollo de futuros modelos dinámicos de evaluación de la degrada­ción de suelos.

 

AGRADECIMIENTOS

Los autores agradecen a la Caja de Aho­rros del Mediterráneo (CAM) la concesión de una beca predoctoral para la realización de este trabajo.

 

REFERENCIAS BIBLIOGRÁFICAS

Agassi, M. & Ben-Hur, M. 1991. Effect of slope length, aspect and phosphogyp­sum on runoff and erosion from steep slopes. Australian Journal of Soil Re­search, 29: 197-207.

Antolín, C. 1998. El suelo como recurso na­tural en la Comunidad Valenciana. Pu­blicaciones de Divulgación Técnica. Co­lección "Territori". Número 8. Generali­tat Valenciana. Valencia, España.

Blum, W.E. 1990. The Challenge of Soil Protection in Europe. Environmental Conservation, 17: 72-74.

Box, Jr., J. & Bruce, R. 1995. The effect of surface cover on infiltration and soil ero­sion. In Agassi, M. (Ed.) Soil Erosion, Conservation and Rehabilitation, pp. 107-123. Marcel Dekker, Inc., New York, USA.

Brandt, C.J. & Thornes J.B. 1996. Mediter­ranean Desertification and Land Use. Wiley, Chichester, UK.

Chuvieco, E. 2002. Teledetección Ambien­tal: la observación de la Tierra desde el Espacio. Ariel, Barcelona, España.

Cohen, S., Svoray, T., Laronne, J. & Alex­androv, Y. 2008. Fuzzy-based dynamic soil erosion model (FuDSEM): Model­ling approach and preliminary evalua­tion. Journal of Hydrology, 356: 185­-198.

Contador, J.F.L., Schnabel, S., Gutiérrez, A.G. & Fernández, M.P. 2009. Mapping sensitivity to land degradation in Extre­madura. SW Spain. Land Degradation & Development, 20: 129-144.

De Paz, J., Sánchez, J. & Visconti, F. 2006. Combined use of GIS and environ­mental indicators for assessment of chemical, physical and biological soil degradation in a Spanish Mediterranean region. Journal of Environmental Man­agement, 79: 150-162.

Eastman, J. 2009. IDRISI Taiga Guide to GIS and Image Processing. Clark Labs. Clark University, Worcester (MA), USA.

Eswaran, H., Lal, R. & Reich, P. 2001. Land Degradation: An overview. In Bridges, E., Hannam, I., Oldeman, L., Pening de Vries, F., Scherr, S. & Som­patpanit, S. (Eds.) Responses to Land Degradation. Proc. 2nd. International Conference on Land Degradation and Desertification. Khon Kaen, Thailand, pp. 20-35. Science Publishers, Inc., En-field (NC), USA,

Holben, B.N. 1986. Characteristics of maximum-value composite images from temporal AVHRR -data. International Journal of Remote Sensing, 7: 1417­1434.

IGN-CNIG. 2005. Atlas Nacional de Espa­ña. Sección II Grupo 7. Edafología. Se­gunda edición. Instituto Geográfico Na­cional (IGN) -Centro Nacional de In­formación Geográfica (CNIG). Ministe­rio de Fomento, Madrid, España.

Jenny, H. 1941. Factors of soil Formation. McGraw-Hill, New York, USA.

Kapur, S. & Akça, E. 2006. Degradation: Global Assessment. In Lal, R. (Ed.) En­cyclopedia of Soil Science, Second Edi­tion, pp. 428-437. Taylor & Francis Group, New York, USA,

Lu, D., Batistella, M., Moran, E. & Mausel, P. 2004. Application of spectral mixture analysis to Amazonian land-use and land-cover classification. International Journal of Remote Sensing, 25: 5345­5358.

MARM. 2008. Programa de Acción Nacio­nal contra la Desertificación (PAND. Convención de las Naciones unidas de Lucha Contra la Desertificación. Minis­terio de Medio Ambiente y Medio Rural y Marino (MARM), Gobierno de Espa­ña, Madrid, España.

McBratney, A.B., Mendonça Santos, M.L. & Minasny, B. 2003. On digital soil mapping. Geoderma, 117: 3-52.

McBratney, A. & Odeh, I. 1997. Applica­tion of fuzzy sets in soil science: Fuzzy logic, fuzzy measurements and fuzzy decisions. Geoderma, 77: 85-113.

Meléndez-Pastor, I., Navarro-Pedreño, J., Gómez, I., Mataix, J. & Jordán, M. 2006. A simplified fuzzy logic model to evaluate soil vulnerability. 1. Theoretical basis: DEM and Remote Sensing. 5th European Congress on Regional Geosci­entific Cartography and Information Sys­tems. Earth and Water. Proceedings Vol­ume I, pp. 182-184.Institut Cartogràfic de Catalunya & Institut Geològic de Cata­lunya, Barcelona, España,

Metternicht, G. & Gonzalez, S. 2005. FUERO: Foundations of a fuzzy ex­ploratory model for soil erosion hazard prediction. Environmental Modelling and Software, 20: 715-728.

Mitra, B., Scott, H., Dixon, J. & McKim­mey, J. 1998. Applications of fuzzy logic to the prediction of soil erosion in a large watershed. Geoderma, 86: 183­209.

Morgan, R. 1997. Erosión y Conservación del Suelo. Mundi-Prensa, Madrid, Espa­ña.

Poch, R. & Martínez-Casasnovas, J. 2006. Degradation. In Lal, R. (Ed.) Encyclo­pedia of Soil Science, Second Edition, pp. 375-378. Taylor & Francis Group, New York, USA.

Rouse, J., Hass, R., Schell, J. & Deering, D. 1974. Monitoring Vegetation Systems in the Great Plains with ERTS. Proceed­ings of the Third Earth Resources Tech­nology Satellite-1 Symposium, pp. 3010-3017. NASA SP-351, Washington D.C., USA,

Torri, D. & Borselli, L. 2000. Water ero­sion. In Sumner, M. (Ed.) Handbook of Soil Science, pp. G171-G194.CRC Press, Boca Raton (FL), USA.

UNEP. 1997. World Atlas of Desertifica­tion. Second edition. United Nations Environment Programme (UNEP), Nai­robi, Kenya.

Wischmeier, W. & Smith, D. 1965. Predict­ing rainfall-erosion losses from cropland east of the Rocky Mountains. Guide for Selection of Practices for Soil and Water Conservation. Agriculture Handbook 282. United States Department of Agri­culture (USDA), Washington D.C., USA.

Zadeh, L. 1965. Fuzzy sets. Information and Control, 8: 338-353.        [ Links ]