Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Similares em
SciELO
Similares em
SciELO
Compartilhar
Revista de Ciências Agrárias
versão impressa ISSN 0871-018X
Rev. de Ciências Agrárias v.33 n.1 Lisboa jan. 2010
Influência do comprimento do sulco sobre a equação de infiltração obtida pelo método dos dois pontos de Elliot & Walker
S. Shahidian1, R.P. Serralheiro1 & J. Serrano1
1 ICAAM, Apartado 94, 7000 Évora, email: shakib@uevora.pt; ricardo@uevora.pt; jmrs@uevora.pt
RESUMO
A Equação de infiltração do tipo Kostiakov pode ser determinada através do método dos dois pontos de Elliot & Walker. No entanto não existem normas para a selecção dos dois pontos. No presente trabalho foram utilizados diferentes pares de pontos ao longo de um sulco com 220m para calcular as correspondentes equações de infiltração. Os resultados demonstram que o expoente a da equação aumenta com o comprimento de sulco considerado, e com a distância até ao ponto do meio. Por sua vez, o coeficiente k tem um comportamento inverso, diminuindo com o aumento do comprimento do sulco. Assim, e por forma a que haja uma uniformidade de critérios, é recomendável que o primeiro ponto esteja o mais próximo da meia distância entre a cabeceira e o segundo ponto.
Palavras-chave: Elliot e Walker, Equações de infiltração, Kostiakov, Rega por sulcos
Influence of furrow length on the infiltration equation obtained by the two point method of Elliot & Walker
ABSTRACT
The Kostiakov infiltration equation can be established by the two point method of Elliot and Walker. Nevertheless, there are no indications as to how the two points should be selected. In this paper different pairs of points along a 220m long furrow are used to calculate the corresponding infiltration equation. The results indicate that the exponent of the equation increases with the length of the furrow, and with distance to the first point. The k of the equation behaves in the opposite direction, decreasing with an increase in the length of the furrow. It is recommended that the first measurement point should be located half way between the furrow inlet and the second measurement point.
Key-words: Elliot & Walker, Infiltration equation. Kostiakov, furrow irrigation
INTRODUÇÃO
A infiltração da água no solo pode ser descrita através de várias equações de infiltração algébricas (Or & Silva, 1996; Elliott & Eisenhauer, 1983; Katopodes et al., 1990). Provavelmente o mais comum é de Kostiakov:
Z kt a (1)
em que Z é a infiltração acumulada expressa em altura de água, ou volume por unidade de comprimento, t é o tempo de infiltração, e k e a são constantes empíricas. A equação de Kostiakov é também aquela que melhor representa a infiltrabilidade dos solos típicos do Alentejo.
Um método muito difundido para o cálculo da equação de infiltração é o método dos dois pontos, proposto por Elliot & Walker (1982). Neste método, medem-se os tempos de avanço até um ponto no meio, tm, e outro no fim do sulco, tf. Utilizando as equações de geometria do sulco (largura, b, e o perímetro molhado, Pm, em função da altura desde o fundo do sulco) calcula-se o volume armazenado superficialmente recorrendo a um coeficiente de armazenamento superficial, y, que normalmente toma o valor de 0,7. Por sua vez, o volume médio infiltrado até ao primeiro e segundo ponto do sulco, Vm,e Vf são obtidos através da realização de um balanço volumétrico.
A equação de infiltração propriamente dita é, finalmente calculada em função do tempo desde o início da rega, pelo método dos dois pontos:
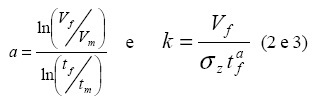
O método dos dois pontos tem sido utilizado com bastante êxito para representar a infiltração em sulcos de qualquer comprimento, não existindo à partida limitações à localização dos dois pontos de medição, estando apenas implícito que o primeiro ponto deve estar localizado próximo do meio do sulco (Serralheiro, 1995). No entanto, pouco se sabe acerca do efeito do comprimento sobre as equações obtidas ou o comprimento ideal do sulco para a determinação rigorosa dos parâmetros da equação. Efectivamente, tem-se observado grandes variações, na prática, quando se utilizam equações de infiltração sem se atender às condições em que foram obtidas (Sohrabi & Behnia, 2007).
Assim, o objectivo do presente estudo é averiguar o efeito da localização dos dois pontos sobre os parâmetros da equação de infiltração obtidos através do método de Elliot e Walker.
MATERIAL E MÉTODOS
O presente estudo foi realizado num Solo Argiluviado Pouco Insaturado, Mediterrâneo Pardo de Materiais não Calcários, de quartzodioritos (Pmg), localizado no Perímetro de Rega de Divor. Foram realizadas quatro regas com um caudal de 0,5 ls-1 em sulcos com 220 m de comprimento e um declive longitudinal de 0,2%. Posteriormente foi sintetizada uma curva de avanço típico a partir dos quatro avanços realizados. A utilização de uma curva de avanço médio tem a vantagem de eliminar os desfasamentos no avanço atribuíveis à irregularidade no perfil longitudinal (Figura 1).
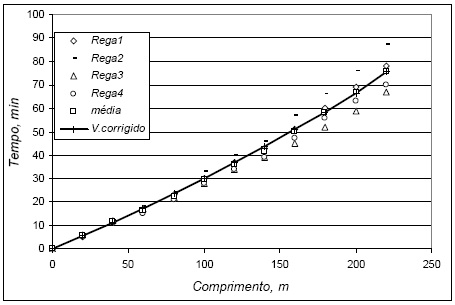
Figura 1-A curva de avanço médio.
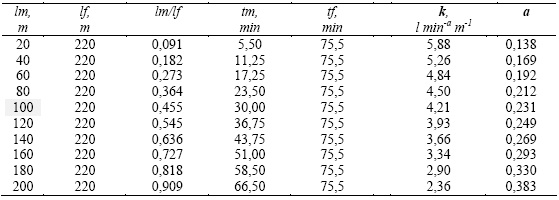
Com base nesta curva de avanço e utilizando valores reais de geometria medidos com recurso a um perfilómetro de barras (Quadro 1), foram considerados 15 diferentes pares de distâncias ao primeiro e segundo ponto, lm e lf. Foram considerados situações com o primeiro ponto exactamente a meia distância entre a cabeceira e o segundo ponto (lm = lf/2), a jusante (lm< lf/2) e a montante (lm > lf/2) da meia distância entre a cabeceira e o segundo ponto.
Quadro 1 -Parâmetros de geometria do sulco utilizados para a determinação da equação de infiltração (b: largura da secção do escoamento, A: a área da secção transversal do sulco, Pm: perímetro molhado e y: a altura desde o fundo do sulco)
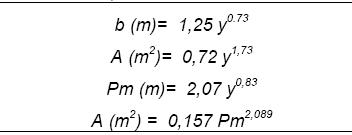
Para cada par de pontos foram calculadas as equações de infiltração do tipo Kostiakov, utilizando o programa CaboGest (Shahidian, 2002) desenvolvido com base na metodologia descrita por Elliot & Walker (1982). As equações obtidas estão apresentadas no Quadro 2.
Quadro 2 -Pares de pontos considerados e os respectivos valores obtidos (sendo lm e lf as distâncias até ao primeiro e segundo ponto, e tm e tf os tempos de avanço até esses pontos).
RESULTADOS E DISCUSSÃO
Apesar de todos os parâmetros de geometria dos sulcos serem praticamente iguais e de se estar a utilizar uma única curva de avanço, verifica-se que o expoente a da equação aumenta com o comprimento de sulco considerado, lf, e com a distância até ao ponto do meio, lm. Por sua vez, o coeficiente k tem um comportamento inverso, diminuindo com o aumento do lm e lf.A Figura 2 mostra claramente a evolução sistemática da equação de infiltração com os pares de distâncias considerados. As curvas sugerem o aumento da infiltração acumulada com o aumento das distâncias consideradas.
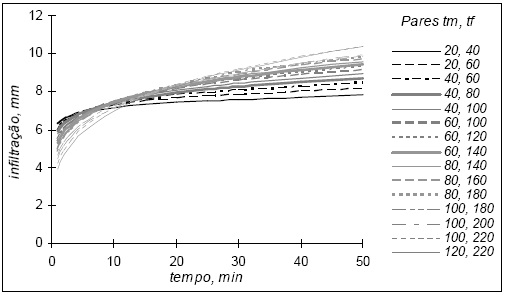
Figura 2 Representação das equações de infiltração obtidas pelo método dos dois pontos, considerando comprimentos progressivamente crescentes de sulco ao longo de uma mesma curva de avanço.
A explicação deste fenómeno reside na relação linear existente entre o expoente a,e a velocidade do avanço até ao fim do sulco (Figura 3a). À medida que a frente do avanço percorre o sulco, a profundidade de escoamento diminui, assistindo-se à redução da velocidade média de avanço. Ou seja, por cada incremento de distância, são necessários intervalos de tempo cada vez maiores para realizar o avanço. O método dos dois pontos interpreta isto como um aumento da infiltração por unidade de comprimento do sulco, e portanto quanto maiores forem os lm e lf considerados, maior será a infiltração calculada. Como o expoente a é calculado a partir da relação Vf/Vm (Equação 2), este aumentará significativamente com o aumento dos comprimentos considerados.
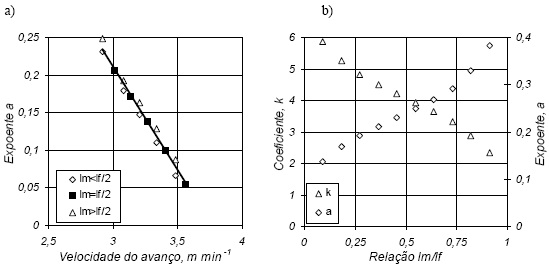
Figura 3-a) Variação do coeficiente a com a velocidade do avanço até ao segundo ponto considerado (lf/tf). b) Influência da posição relativa do primeiro ponto considerado sobre o valor dos parâmetros da equação de infiltração, k em l min-a m-1, e a.
Como uma parte do módulo parcelar infiltra no sulco, à medida que a frente do avanço vai percorrendo o sulco, a secção submersa vai diminuindo. De facto, se no primeiro metro dum sulco, a quase totalidade do caudal aplicado estará à superfície e portanto o coeficiente de armazenamento superficial, y, será muito próximo da unidade, aos 200 m do sulco a secção será atravessada por apenas uma pequena fracção do caudal aplicado à cabeceira do sulco, e portanto o armazenamento superficial será pequeno.
Relativamente ao posicionamento exacto do primeiro ponto, lm, observa-se que a sua localização afecta significativamente os parâmetros da equação de infiltração determinados pelo método dos dois pontos (Figura 3b e Quadro 3), embora o seu efeito seja menor do que o do comprimento total dosulco considerado. À medida que a posição do primeiro ponto se afasta do meio do sulco, os valores de k e a sofrem distorções cada vez maiores. O valor do a diminui ou aumenta, consoante o primeiro ponto se aproxima ou afasta da cabeceira, respectivamente.
Quadro 3 -Efeito da localização do primeiro ponto, lm sobre o coeficiente e expoente da equação de Kostiakov.
CONCLUSÕES
Embora os parâmetros da equação de infiltração sejam características do solo, os resultados obtidos indicam que não deixam de ser afectados pelos comprimentos considerados para a medição do avanço. Para um determinado sulco e rega, verifica-se que o expoente a da equação aumenta com o comprimento de sulco considerado, lf, e com a distância até ao ponto do meio, lm. Por sua vez, o coeficiente k tem um comportamento inverso, diminuindo com o aumento do lm e lf. Os resultados obtidos indicam claramente o aumento da infiltração acumulada com o aumento das distâncias consideradas.
Assim, e por forma a que haja uma uniformidade de critérios, recomenda-se que o primeiro ponto, lm, esteja o mais próximo da meia distância entre a cabeceira e o segundo ponto, lf.
No método dos dois pontos o expoente a da equação de infiltração é determinado em função das relações entre os volumes infiltrados ao fim e ao meio do sulco e dos tempos até ao fim e meio do sulco, pelo que, o seu valor é muito sensível às alterações na relação tm/tf. À medida que a duração do avanço nas duas metades do sulco se aproximam, o valor do expoente diminui, aproximando-se do zero. Deste modo, em solos com grande infiltrabilidade, onde a velocidade de escoamento diminui bastante ao longo do sulco, o valor do a será elevado, enquanto que em solos com baixa infiltrabilidade, a velocidade de escoamento será semelhante ao longo de todo o sulco, obtendo-se um a reduzido. Se a duração do avanço na primeira metade do sulco for superior ao da segunda metade, o expoente apresentará um valor negativo, o que não acontecerá sob condições normais.
REFERÊNCIAS BIBLIOGRÁFICAS
Elliott, R.L. & Eisenhauer, D.E. 1983. Volume balance techniques for measuring infiltration in surface irrigation. ASAE Winter meeting paper 83.
Elliot, R.L. & Walker, W.R. 1982. Field evaluation of furrow infiltration and advance functions. Transactions of the ASAE, 25(2): 396-400.
Or, D. & Silva, H.R. 1996. Prediction of surface irrigation advance using soil intake properties, Irrigation Science, 16: 159-167. [ Links ]
Katopodes, N.D., Tang, J.H. & Clemmens, A.J. 1990. Estimation of surface irrigation parameters, Jour. of Irrigation and Drainage Eng., 116(5): 676-694
Serralheiro, R.P. 1995). Furrow irrigation advance and infiltration equations for a Mediterranean soil. Jour. Agricultural Engineering Research, 62: 117-126.
Shahidian, S. 2002. Automação da Rega de Superfície com Retorno, em Tempo Real, da Informação do Campo. Tese apresentada à Universidade de Évora para obtenção de grau de doutor. Évora.
Sohrabi, B. & Behnia, A. 2007. Evaluation of Kostiakovs Infiltration Equation in Furrow Irrigation Design According to FAO Method. Journal of Agronomy, 6 (3): 468-471.














