Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Similares em
SciELO
Similares em
SciELO
Compartilhar
Revista de Ciências Agrárias
versão impressa ISSN 0871-018X
Rev. de Ciências Agrárias vol.41 no.2 Lisboa jun. 2018
https://doi.org/10.19084/RCA17278
ARTIGO
Secagem e difusividade de sementes de melão
Drying and diffusivity of melon seeds
Isneider L. Silva1*, Hellismar W. da Silva2, Fernando R. T. de Camargo1, Hiago F. L. de Farias1 e Elaine de F. M. Freitas1
1 Universidade Estadual de Goiás, Campus Ciências Exatas e tecnológicas - Henrique Santillo (CCET), Anápolis, Goiás, Brasil
2 Universidade Federal de Lavras, Lavras, Minas Gerais, Brasil
(*-Email: Isneider.luiz@gmail.com)
RESUMO
As sementes do melão contêm alto teor de água após a extração, necessitando da secagem para manter as suas qualidades fisiológicas. O objetivo deste trabalho consistiu em modelar curvas de secagem das sementes de melão em diferentes temperaturas, determinar o coeficiente de difusão efetivo e a energia de ativação. A secagem foi realizada em condições controladas, nas temperaturas de 35, 40, 45, e 50 °C, utilizando-se três repetições de 10 g de sementes, as quais foram pesadas periodicamente até atingirem massa constante. Os dados experimentais foram ajustados a diferentes modelos matemáticos frequentemente utilizados na representação da secagem de sementes. O coeficiente de difusão efetivo, calculado a partir do modelo matemático da difusão líquida para esferoide prolato, foi utilizado para obtenção da energia de ativação. Os resultados evidenciaram que o modelo de Page é o que melhor se ajusta aos dados experimentais. A elevação da temperatura de secagem reduz o tempo de secagem e promove aumento do coeficiente de difusão efetivo. A relação do coeficiente de difusão com a temperatura de secagem pode ser descrita pela equação de Arrhenius, apresentando uma energia de ativação de 55,81 kJ mol-1 no processo de secagem das sementes de melão.
Palavras-chave: difusão, energia de ativação, modelagem matemática, secagem.
ABSTRACT
The melon seeds contain high water content after extraction, requiring drying to maintain their physiological qualities. The objective of this work was to model drying curves of melon seeds at different temperatures, to determine the effective diffusion coefficient and the activation energy. Drying was carried out under controlled conditions at temperatures of 35, 40, 45, and 50 °C using three replicates of 10 g of seeds, which were weighed periodically until reaching constant mass. The experimental data were adjusted to different mathematical models frequently used in the representation of seed drying. The effective diffusion coefficient, calculated from the mathematical model of net diffusion to spheroid prolat, was used to obtain the activation energy. The results showed that the Page model is the one that best fits the experimental data. The increase of the drying temperature reduces the drying time and promotes an increase of the effective diffusion coefficient. The relation of the diffusion coefficient to the drying temperature can be described by the Arrhenius equation, presenting an activation energy of 55.81 kJ mol-1 in the drying process of the melon seeds.
Keywords: activation energy, diffusion, drying, mathematical modeling
INTRODUÇÃO
O melão (Cucumis melo L.) é uma cucurbitácea cultivada em várias regiões do mundo e tem grande expressão económica. As sementes de melão, bem como de outras culturas, ao serem extraídas dos frutos carnudos, apresentam alto teor de água, próximos de 65% (base úmida), fazendo com que seja necessária secagem para que a qualidade fisiológica não decaia (Guimarães et al., 2013).
O uso de modelos matemáticos é utilizado para simular o processo de secagem de sementes, cujo princípio se fundamenta na secagem de camadas delgadas ou finas do produto (Reis et al., 2011), assim, a perda de água da semente durante o processo de secagem pode ser muito bem representada por esses os modelos matemáticos (Mendonça et al., 2015).
O estudo da modelagem matemática da cinética de secagem já é muito utilizado por diversos investigadores e também para diferentes produtos. Na literatura, podem encontrar-se modelos matemáticos que têm sido utilizados para descrever a cinética de secagem de diversos produtos agrícolas, tais como sementes de cambre (Crambe abyssinica Hortsh Ex. R. T.; Faria et al., 2012), frutos de pimenta-cabacinha (Capsicum chinense L.; Silva et al., 2016), sementes de abóbora (Cucurbita moschata Duchesne; Diógenes et al., 2013), sementes de feijão (Vigna unguiculata (L.) Walp¸Camicia et al., 2015).
O coeficiente de difusão (Def) engloba os efeitos de todos os fenômenos que podem intervir sobre a migração da água, e seu valor é obtido pelo ajuste de valores experimentais. Todavia, pode-se entender a difusividade como a facilidade com que a água é removida do material (Reis et al., 2011).
Na literatura os estudos com cinética de secagem de sementes de melão ainda são escassos, o que torna necessário a obtenção de informações. De acordo com o exposto, o objetivo do presente trabalho foi estudar o ajuste de curvas de secagem para sementes de melão nas temperaturas de 35, 40, 45 e 50 °C, como também estimar o coeficiente de difusividade efetiva (Def) e a energia de ativação (Ea).
MATERIAL E MÉTODOS
Este trabalho foi desenvolvido no Laboratório de Secagem e Armazenamento de Produtos Vegetais do Campus de Ciências e Exatas e Tecnológicas - Henrique Santillo, da Universidade Estadual de Goiás em Anápolis – GO, Brasil.
Foram utilizadas sementes de melão amarelo (Cucumis melo L.) produzidas no município de Anápolis-GO, com coordenadas geográficas centrais 16º 22 22 de latitude Sul e 48º 53 08 de longitude Oeste e 1.012 m de altitude. O clima da região de acordo com a classificação de Köppen é do tipo Aw, com inverno seco e verões quentes e chuvosos (Pereira et al., 2002). As sementes foram extraídas manualmente, lavadas em água corrente, homogeneizadas, acondicionadas em saco plástico e armazenadas por dois dias em frigorífico (4 °C) até à instalação do ensaio (Camicia et al., 2015).
Antes de cada ensaio de secagem, as amostras foram retiradas do frigorífico e mantidas à temperatura ambiente, durante cerca de 6-h, visando homogeneizar a temperatura. O teor de água das sementes no início da secagem foi de aproximadamente 65,28±0,20% (b.u.). Para cada temperatura de secagem foram utilizadas três repetições com 10 g de sementes em camada única, as quais foram colocadas em recipientes com o fundo em tela. O processo de secagem das sementes foi realizado em estufa com sistema de circulação forçada de ar ajustada para as temperaturas de 35, 40, 45 e 50 °C e UR de 42, 37, 32 e 26 %, respectivamente.
Durante o processo de secagem as amostras foram pesadas periodicamente em balança analítica (precisão de 0,001 g) até que as sementes atingissem o equilíbrio higroscópico, com as condições do ar de secagem, ou seja, quando a variação de massa fosse constante na segunda casa decimal por três pesagens consecutivas (Melo et al., 2016a; Silva et al., 2016). Para o cálculo da razão de umidade (RX), durante as secagens nas diferentes temperaturas, foi utilizada a Equação 1 (Camicia et al., 2015; Coradi et al., 2015).
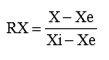 (1)
(1)
em que:
X = teor de água do produto, decimal (b.u);
Xe = teor de água de equilíbrio do produto, decimal (b.u);
Xi = teor de água inicial do produto, decimal (b.u).
Aos dados experimentais da secagem do melão foram ajustados modelos matemáticos empíricos e semi-empíricos, frequentemente utilizadas para representação da secagem de produtos agrícolas (Faria et al., 2012; Melo et al., 2016a; Silva et al., 2016), cujas expressões estão apresentadas na Quadro 1.
Para o ajuste dos modelos matemáticos de secagem aos dados experimentais, foi realizada análise de regressão não linear pelo método Quasi-Newton, utilizando o programa Statistica 10. O grau de ajuste de cada modelo considerou a magnitude do coeficiente de determinação ajustado (R2), o erro médio relativo (P), o erro médio estimado (SE) e o valor do Qui-Quadrado (χ2) conforme descrito nas Equações 11, 12 e 13, respectivamente (Siqueira et al., 2012; Melo et al., 2016b; Silva et al., 2016):
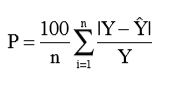 (11)
(11)
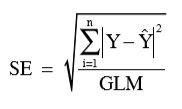 (12)
(12)
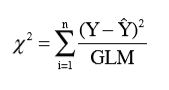 (13)
(13)
em que:
Y= valor observado experimentalmente;
 = valor estimado pelo
modelo;
= valor estimado pelo
modelo;
n = número de observações experimentais;
GLM = graus de liberdade do modelo (número de observações menos o número de parâmetros do modelo).
O coeficiente de difusão efetivo (Def) foi obtido por meio do ajuste do modelo matemático da difusão líquida (Equação 14), com aproximação de oito termos, aos dados experimentais da secagem das sementes de melão. Essa equação é a solução analítica para a segunda lei de Fick, considerando a forma geométrica do produto como esferoide prolato, desconsiderando a contração volumétrica e considerando a condição de contorno de teor de água conhecida na superfície da semente (Brooker et al., 1992).
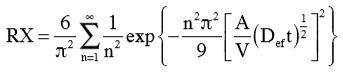 (14)
(14)
em que:
n = número de termos;
A = área superficial do produto, (m2);
V = volume do produto, (m3).
Para calcular o volume e a área superficial, 50 sementes tiveram os eixos ortogonais (comprimento, largura e espessura) mensurados com o auxílio de um paquímetro digital com resolução de 0,001 mm, conforme as seguintes expressões (Mohsenin, 1986)
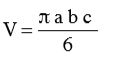 (15)
(15)
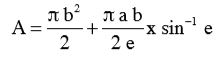 (16)
(16)
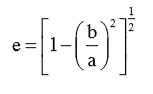 (17)
(17)
em que:
a = maior eixo do produto, (m);
b = eixo médio do produto, (m);
c = menor eixo do produto, (m);
e = excentricidade, adimensional.
Para avaliar a influência da temperatura de secagem sobre o coeficiente de difusão efetivo os dados foram ajustados à equação de Arhenius (Equação 18) (Diógenes et al., 2013):
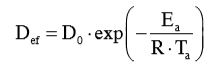 (18)
(18)
onde:
D0 = Fator Pré exponencial (m2 s-1);
Ea = Energia de ativação (KJ mol-1);
R = Constante universal dos gases, 8,314 kJ mol-1 K-1;
Ta = Temperatura absoluta (K).
RESULTADOS E DISCUSSÃO
As comparações entre os modelos de secagem analisados são apresentadas no Quadro 2, com os valores dos parâmetros estatísticos coeficientes de determinação (R²), erros médios relativo (P), estimado (SE) e qui-quadrado X2 para os modelos ajustados de secagem de melão amarelo, nas temperaturas de 35, 40, 45 e 50 °C.
Todos os modelos ajustados, para todas as temperaturas apresentaram coeficiente de determinação (R²) superior à 98%. Porém, o coeficiente de determinação isoladamente não constitui um bom parâmetro para a seleção de modelos não lineares; desta forma utilizou-se o valor do erro médio relativo (P) e estimado (SE). De acordo com Draper e Smith (1998), quanto menor o valor de P, SE e χ 2 maior a precisão.
Dentre a série testada o modelo de Page foi o que apresentou um melhor ajuste aos dados experimentais para todas as temperaturas, com elevados valores do coeficiente de determinação (R²), estando para todos os tratamento acima de 99% e com os menores valores de P, SE e χ2 .
Jittanit (2011) no seu trabalho com secagem de sementes de abóbora, também encontrou um melhor ajuste para os dados experimentais com o modelo de Page. Já Diógenes et al. (2013) ao ajustar modelos matemáticos para grãos de abóbora, que são morfologicamente semelhantes às sementes de melão, para as temperaturas de 40, 50, 60 e 70 °C encontrou um melhor ajuste para a Aproximação da difusão.
O tempo necessário para as sementes de melão amarelo alcançarem o equilíbrio higroscópico foi de 5,87; 4,91; 4,65 e 3,42-h nas temperaturas de 35, 40, 45 e 50 °C, respectivamente (Figura 1).
Após o processo de secagem das sementes de melão amarelo os teores de água de equilíbrio das amostras foram de 13,4; 10,2; 8,5 e 4,7 % base úmida, para as temperaturas de 35, 40, 45 e 50 °C, respectivamente.
A Figura 1 apresenta um bom ajuste do modelo de Page na descrição dos resultados experimentais e o cálculo da razão de umidade em função do tempo de secagem. Com o aumento da temperatura do ar de secagem ocorreu maior taxa de remoção de água do produto, concordando com diversos investigadores para vários produtos agrícolas, designadamente Coradi et al. (2015) para grãos de milho, Silva et al. (2016) para frutos de pimenta e Melo et al. (2016a) para grãos de feijão-carioca.
As curvas obtidas (Figura 1) demonstram para todas as temperaturas que o teor de umidade existente é reduzido com o aumento da temperatura do ar de secagem, até alcançar o teor de umidade de equilíbrio. Estes resultados estão de acordo com os trabalhos realizados sobre a secagem de diversos produtos como para curvas de secagem de grão de abobora (Diógenes et al., 2013) e de sementes de feijão-caupi (Camicia et al., 2015).
No Quadro 3 estão apresentados os valores dos coeficientes do modelo ajustado de Page, para cada temperatura.
Com relação aos valores da difusividade efetiva (Def), notou-se que aumentaram com a elevação da temperatura de secagem (Quadro 4), com valores de 1,553 x 10-10 m² s-1; 1,709 x 10-10 m² s-1; 1,917 x 10-10 m² s-1 e 2,091 x 10-10 para as temperaturas de 35, 40, 45 e 50 °C, respectivamente. Quando as temperaturas são elevadas a viscosidade da água diminuiu, facilitando a sua remoção das sementes (Reis et al., 2011).
Jittanit (2011) trabalhando com sementes de abóbora verificou valores de 3,76 × 10-10 a 5,09 × 10-10 para as temperaturas 60, 70 e 80 ºC. Guiné et al. (2012) secando também sementes de abóbora a temperaturas entre 30 e 70 °C, constataram o aumento dos valores do coeficiente de difusão conforme a elevação da temperatura do ar de secagem.
Constatou-se, na presente situação, que a energia de ativação para difusão líquida das sementes de melão amarelo, foi de aproximadamente 55,81 kJ mol-1 (valor obtido na resolução da equação 18). Destaca-se que nos processos de secagem quanto menor a energia de ativação maior será a difusividade de água no produto (Melo et al., 2016b).
A energia de ativação encontrada neste trabalho foi maior que a encontrada por Silva et al. (2016), cujo valor foi de 36,09 kJ mol-1 durante a secagem de frutos de pimenta com faixa de temperatura de 60 a 100 ºC. Estas diferenças surgem porque os valores de energia de ativação variam de acordo com a higroscopicidade do produto, a sua morfologia e as condições ambientais em que estão encontradas. Jittanit (2011) e Guiné et al. (2012) estudaram a secagem das sementes de abóbora, porém encontraram valores diferentes de energia de ativação.
CONCLUSÕES
O modelo matemático de Page apresentou o melhor ajuste aos dados experimentais nas diferentes condições de secagem.
As sementes entraram em equilíbrio higroscópico com 13,4; 10,2; 8,5 e 4,7 % base úmida, com o tempo de 5,87; 4,91; 4,65 e 3,42 horas, para as temperaturas de 35, 40, 45 e 50 °C, respectivamente.
O coeficiente de difusão aumenta com a elevação da temperatura, apresentando valores entre 1,553 x 10-10 a 2,091 x 10-10, para a faixa de temperatura de 35 à 50 ºC, respectivamente.
A relação entre o coeficiente de difusão efetivo e a temperatura de secagem pode ser descrita pela equação de Arrhenius, que apresenta uma energia de ativação de 55,81 kJ mol-1.
Referências Bibliográficas
Brooker, D.B.; Bakker-Arkema, F.W. & Hall, C.W. (1992) - Drying and Storage of Grains and Oilseeds. Westport: The AVI Publishing Company, 450 p. [ Links ]
Camicia, R.G.M.; Christ, D.; Coelho, S.R.M. & Camicia, R.F.M. (2015) - Modelagem do processo de secagem de sementes de feijão-caupi. Revista Caatinga, vol. 28, n. 3, p. 206–214. http://dx.doi.org/10.1590/1983-21252015v28n323rc [ Links ]
Coradi, P.C.; Milane, L.V.; Dias, C.F. & Baio F.H.R. (2015) - Mathematical modeling of drying maize grains in different temperatures. Revista Brasileira de Milho e Sorgo, vol. 14, n. 2, p. 247-259. http://dx.doi.org/10.18512/1980-6477/rbms.v14n2p247-259 [ Links ]
Diógenes, A.M.G.; Queiroz, A.J.M.; Fiqueiredo, R.M.F. & Santos, D.C. (2013) - Cinética de secagem de grãos de abóbora. Revista Caatinga, vol.26, n. 1, p. 71-80. [ Links ]
Draper, N.R. & Smith, H. (1998) - Applied regression analysis. 3ª ed. New York: John Wiley & Sons, 712 p. [ Links ]
Faria, R.Q.; Teixeira, I.R.; Devilla, I.A.; Ascheri, D.P.R. & Resende, O. (2012) - Cinética de secagem de sementes de Crambe. Revista Brasileira de Engenharia Agrícola e Ambiental, vol. 16, n. 5, p. 573-583. http://dx.doi.org/10.1590/S1415-43662012000500014 [ Links ]
Guimarães, M.A.; Telles, J.P.F.; Dasmaceno, L.A.; Viana, C.S. & Monteiro, L.R. (2013) - Pré-embebição de sementes e seus efeitos no crescimento e desenvolvimento de plântulas de melancia. Revista Ceres, vol. 60, n. 3, p. 442-446. [ Links ]
Guiné, R.P.F.; Henrriques, F. & Barroca, M.J. (2012) - Mass Transfer Coefficients for the Drying of Pumpkin (Cucurbita moschata) and Dried Product Quality. Food and Bioprocess Technology, vol. 5, n. 1, p. 176–183. http://dx.doi.org/10.1007/s11947-009-0275-y [ Links ]
Jittanit, W. (2011) - Kinetics and Temperature Dependent Moisture Diffusivities of Pumpkin Seeds During Drying. Kasetsart Journal-Natural Science, vol.45, n. 1, p. 147–158. [ Links ]
Melo, P.C.; Devilla, I.A.; Caetano, J.M.; Reis, V.B.S.; Antunes, A.M. & Santos M.M. (2016a) - Modelagem matemática das curvas de secagem de grãos de feijão carioca. Revista Brasileira de Ciências Agrárias, vol. 11, n. 3, p. 247-252. [ Links ]
Melo, P.C.; Devilla, I.A.; Lisboa, C.F.; Santos, M.M. & Duarte, P.H.T. (2016b) - Kinetics drying of Spirulina platensis. African Journal of Agricultural Research, vol. 11, n. 45, p. 4683-4691. http://dx.doi.org/10.5897/AJAR2016.11678 [ Links ]
Mendonça, A.P.; Sampaio, P.T.B.; Almeida, F.A.C.; Ferreira, R.F. & Novais, J.N. (2015) - Determinação das curvas de secagem das sementes de andiroba em secador solar. Revista Brasileira de Engenharia Agrícola e Ambiental, vol. 19, n. 4, p. 382-387. http://dx.doi.org/10.1590/1807-1929/agriambi.v19n4p382-387 [ Links ]
Mohsenin, N.N. (1986) - Physical properties of plant and animal materials. 2 ed. New York: Gordon and Breach Publishers. 841p. [ Links ]
Reis, R.C.; Barbosa, L.S.; Lima, M.L.; Reis, J.S.; Devilla, I.A. & Ascheri, D.P.R. (2011) - Modelagem matemática da secagem da pimenta cumari do Pará. Revista Brasileira de Engenharia Agrícola e Ambiental, vol. 15, n. 4, p. 347–353. http://dx.doi.org/10.1590/S1415-43662011000400003 [ Links ]
Silva, H.W.; Rodovalho, R.S.; Velasco, M.F.; Silva, C.F. & Vale, L.S.R. (2016) - Kinetics and thermodynamic properties related to the drying of Cabacinha pepper fruits. Revista Brasileira de Engenharia Agrícola e Ambiental, vol. 20, n. 2, p. 174-180. http://dx.doi.org/10.1590/1807-1929/agriambi.v20n2p174-180 [ Links ]
Siqueira, V.C.; Resende, O. & Chaves, T.H. (2012) - Drying kinetics of Jatropha seeds. Revista Ceres, vol. 59, n. 2, p. 171-177. http://dx.doi.org/10.1590/S0034-737X2012000200004 [ Links ]
Recebido/received: 2017.11.02
Recebido em versão revista/received in revised form: 2018.01.03
Aceite/accepted: 2018.01.03














