INTRODUÇÃO
A altura dominante apresenta um papel importante na tomada de decisão, pois permite avaliar e classificar o potencial produtivo de um determinado local. Contudo, nos inventários florestais tradicionais as variáveis são obtidas assumindo o pressuposto de que a sua média é constante em toda a população (Mello et al., 2009). Por outro lado, a posição das unidades amostrais pode influenciar no valor da variável desejada, sendo importante considerar tal efeito nas análises, permitindo maximizar o uso das informações disponíveis na área.
A variabilidade espacial desses valores pode ser obtida por métodos determinísticos e geoestatísticos, baseado na suposição de que as unidades amostrais vizinhas possuem maior similaridade entre si, em relação àquelas mais distantes, no espaço e tempo (Yamamoto e Landim, 2013). Os interpoladores espaciais diferenciam-se na forma como os ponderadores são calculados.
Na interpolação determinística, as estimativas são obtidas por meio da ponderação dos valores observados nos pontos vizinhos ao ponto de interesse (Negreiros et al., 2008), desconsiderando a estrutura de dependência espacial da variável, se presente. Este método não utiliza a teoria da probabilidade e prediz estimativas com base na combinação linear das unidades amostrais em função da sua distribuição no espaço (Mazzini & Schettini, 2009). Por isso, o mapeamento das incertezas não é possível com essa abordagem.
Os mais utilizados são o inverso do quadrado da distância e a interpolação polinomial (Mazzini & Schettini, 2009; Xie et al., 2011). O primeiro considera que a influência das amostras vizinhas é inversamente proporcional à distância quadrática euclidiana em relação ao ponto não amostrado (Alves & Vecchia, 2011). A interpolação polinomial global, por sua vez, é uma função matemática e consiste em caracterizar e descrever as tendências gerais de uma superfície de interesse (Negreiros et al., 2008; Li & Heap, 2014).
A geoestatística, por outro lado, baseia-se no estudo das variáveis regionalizadas (Yamamoto & Landim, 2013). Utilizando a semivariância como medida estatística básica, os semivariogramas experimentais e teóricos permitem caracterizar e modelar a dependência espacial das variáveis regionalizadas (Pelissari et al., 2014). Além disso, a ponderação das unidades amostrais é baseada em critérios probabilísticos, permitindo também a espacialização das zonas de incerteza associadas aos pontos preditos (Yamamoto & Landim, 2013).
Dentre os métodos de estimativa geoestatísticos, a krigagem e a cokrigagem são os mais abordados na literatura (Mello et al., 2005a; Guedes et al., 2015; Lundgren et al., 2015, 2016; Benítez et al., 2016; Scolforo et al., 2016; Pelissari et al., 2017; Santos et al., 2017). A cokrigagem baseia-se na covariância entre duas ou mais variáveis regionalizadas relacionadas, sendo apropriada a cenários em que o principal atributo de interesse é escasso, mas a informação secundária é abundante (Yamamoto & Landim, 2013).
Por apresentar-se geralmente com forte dependência espacial (Mello et al., 2005b; Guedes et al., 2015), a altura dominante em povoamentos florestais pode ser espacializada para indicar a capacidade produtiva de um local (Mello et al., 2005b). A sua espacialização permite, a partir da criação de zonas homogêneas de manejo, adotar práticas de silvicultura de precisão ao longo do ciclo da cultura (Pelissari et al., 2012).
Assim, levantam-se os seguintes questionamentos: i) a altura dominante apresenta estrutura de dependência espacial em povoamento de eucalipto? ii) Os métodos de estimativas geoestatísticos são mais precisos e exatos em relação aos determinísticos? A hipótese desse trabalho considera que a altura dominante apresenta forte dependencia espacial e os métodos geoestatísticos apresentam melhor desempenho na sua estimativa espacial. Nesse contexto, o objetivo deste estudo foi verificar a estrutura espacial da altura dominante em povoamento de eucalipto, comparando métodos determinísticos e geoestatísticos na estimativa.
MATERIAL E MÉTODOS
Área de estudo
Os dados utilizados foram coletados em povoamento de Eucalyptus sp., com 377 hectares, localizado no município de Bocaiúva, noroeste de Minas Gerais. Foram mensurados 14 talhões, com idades de 6,5 a 7,25 anos e espaçamento médio de 3 x 3 m. A altitude média da região é de 820 m e o clima local, segundo a classificação de Köppen, é definido como tropical úmido de savana (tipo Aw), de inverno seco e verão chuvoso (Alvares et al., 2014), apresentando temperatura e precipitação média anual de 24 ºC e 1.246 mm, respectivamente (Caldeira et al., 2005).
Banco de dados
Os dados foram coletados em 233 unidades amostrais, com área fixa de 200 m² (10 x 20 m) cada, utilizando o processo de amostragem sistemática, equivalendo a intensidade amostral de 1,23 %. Nas unidades amostrais foram mensurados o diâmetro a 1,30 m do solo (DAP) e a altura das árvores dominantes (Hd), segundo o conceito de Assmann (Scolforo & Thiersch, 2004). Em cada unidade amostral obteve-se os valores médios das variáveis de interesse e extraiu-se a respectiva coordenada central, para a posterior análise espacial. A presença de valores extremos foi avaliada pelo teste de Grubbs, ambos com 5% de probabilidade.
Interpoladores espaciais
Os interpoladores utilizados na estimativa espacial da altura dominante foram os geoestatísticos, krigagem e cokrigagem ordinárias (Yamamoto & Landim, 2013), e os métodos determinísticos, polinômio global do 10º grau (Negreiros et al., 2008) e inverso do quadrado da distância (Li & Heap, 2014). De forma complementar, aplicou-se a krigagem indicatriz (Yamamoto & Landim, 2013) para estimar a probabilidade de ocorrência de locais com valores de altura dominante acima da média.
Na krigagem ordinária, foi construído o semivariograma experimental (Equação 1) (Yamamoto & Landim, 2013) para obter os parâmetros iniciais efeito pepita ( C 0 ), contribuição (C) e alcance (a). Também foram analisados os semivariogramas direcionais (0º, 45º, 90º e 135º) a fim de verificar a existência de anisotropia, os quais confirmaram comportamento isotrópico da variável. O semivariograma experimental foi utilizado para o ajuste dos modelos esférico (Equação 2), exponencial (Equação 3) e gaussiano (Equação 4) pelo método da máxima verossimilhança.
Em que γ(h) = semivariância estimada entre pares de pontos; N(h) = número de pares de valores medidos z( x i ), z( x i + h), separados pela distância h.
Em que C 0 = efeito pepita; C = contribuição; a = alcance.
A qualidade de ajuste dos modelos ao semivariograma experimental foi avaliada por meio do erro médio reduzido ( ER ) (Equação 5) e desvio padrão dos erros reduzidos (Ser) (Equação 6), obtidos a partir da validação cruzada, concomitantemente com o critério de informação de Akaike (Equação 7). O AIC mede a distância da curva de um modelo ajustado a uma curva padrão (Araújo et al., 2018a). O menor AIC em conjunto com ER mais próximo de zero e Ser mais próximo de um, representam melhor qualidade do ajuste e ausência ou mínima tendência associada às estimativas.
Em que: z x i0 = valor observado no ponto i0; z x i0 = valor estimado no ponto i0; σ x i0 = desvio padrão da krigagem no ponto i0; L = máxima verossimilhança do modelo candidato; K = número de parâmetros do modelo.
Utilizando os parâmetros dos modelos ajustados, foi estimado o índice de dependência espacial (IDE= C C 0 + C , onde a dependência espacial foi classificada como baixa (IDE ≤ 25%), moderada (25% < IDE ≤ 75%) e forte (IDE > 75%), conforme descrito por Zimback (2003). Comprovada a dependência espacial, aplicou-se a krigagem ordinária (Equação 7) para predizer as estimativas em locais não amostrados. Os pesos ótimos foram obtidos a partir da variância mínima do erro sob a condição de não viés, conforme a restrição imposta pela equação 8 (Yamamoto & Landim, 2013).
Em que Z x 0 = estimativa no ponto não amostrado; Z x i = valor observado no i-ésimo ponto amostral; n = número de pontos amostrados; λ i = peso associado aos i-ésimos pontos amostrados (i = 1,2,3,...,n).
A dependência espacial conjunta entre a altura dominante e o diâmetro a 1,30 m do solo (DAP), medidas nas mesmas unidades amostrais (isotopia), foi descrita e caracterizada pelo semivariograma cruzado (Equação 09). A presença do modelo de corregionalização linear foi verificada pela estruturação dos semivariogramas diretos e cruzado, em conjunto com a condição de proporcionalidade, expressa pela equação 10 (Isaacs & Srivastava, 1989). A correlação linear de Pearson (R) entre essas variáveis também foi calculada.
Em que γ 11 = semivariância estimada da variável primária; γ 22 = semivariância estimada da variável secundária; γ 12 = semivariância cruzada estimada entre pares de pontos; Z 1 = variável primária (Hd); Z 2 = variável secundária (DAP).
A cokrigagem ordinária (Equação 11) objetiva utilizar a dependência espacial conjunta para maximizar o uso das informações espaciais disponíveis, a partir da medição de uma covariável regionalizada mais densamente amostrada (Yamamoto & Landim, 2013).
Em que Z 1 x 0 = estimativa da variável primária no ponto não amostrado; Z 1 x 1i = valor da variável primária observada no i-ésimo ponto amostral; Z 2 x 1j = valor da variável secundária observada no j-ésimo ponto amostral; λ 1i = peso associado a variável primária nos i-ésimos pontos amostrados (i = 1,2,3,...,n); λ 2j = peso associado a variável secundária nos j-ésimos pontos amostrados (j = 1,2,3,...,n).
Com a krigagem indicatriz (Equação 12) foi possível espacializar a probabilidade de ocorrência de sítios mais produtivos, a partir da transformação binária dos valores de altura dominante em cada unidade amostral. Valores acima da média da variável (valor de corte) foram transformados em 1 e valores abaixo, em 0. Em seguida, foi construído o semivariograma indicador na avaliação da estrutura de dependência espacial do novo conjunto de dados (Motomiya et al., 2006).
Em que F u; Z x n = valor estimado no local u para o valor de corte Z x baseado em n amostras vizinhas de u; Z x = valor de corte; i u; Z x = estimador da probabilidade de que a variável Z na localização j seja maior ou menor que Z x ; λ j = peso associado a variável primária nos j-ésimos pontos amostrados (j = 1,2,3,...,n).
Na interpolação determinística, foi avaliado o polinômio global do 10º grau (Equação 13) (Negreiros et al., 2008; Xie et al., 2011) e o inverso do quadrado da distância (Alves & Vecchia, 2011). A interpolação pelo inverso do quadrado da distância é dada pela seguinte expressão (Equação 14).
Em que β’s = coeficientes da regressão; X n = coordenadas geográficas do ponto amostrado; ε = erro aleatório; d i ² = distância quadrática euclidiana.
A qualidade da interpolação espacial, nos diferentes métodos, foi avaliada por meio do erro médio reduzido ( ER ), desvio padrão dos erros reduzidos (Ser), coeficiente de correlação de Pearson (R), coeficiente de determinação (R²) e índice de concordância de Willmott (d), na qual os valores estimados em cada unidade amostral foram obtidos a partir da validação cruzada.
A exatidão de cada método foi avaliada por meio do ajuste de uma regressão linear simples (y= β 0 + β 1 . X i + e i ), com os valores estimados em função dos observados. As hipóteses H 0 : β 0 = 0 e H 0 : β 1 = 1 foram testadas pelo teste F, com 95 % de probabilidade, em que, se aceitas, verificou-se que os valores estimados são estatisticamente próximos dos paramétricos, demonstrando alto nível de exatidão, caracterizado pela linha de regressão com inclinação de 45º ( β 1 = 1) passando pela origem ( β 0 = 0) (Scolforo et al., 2016).
O índice de desempenho (c), descrito por Araújo et al. (2018b), foi utilizado para avaliar o desempenho baseado na precisão e exatidão dos métodos. Deste modo, a associação entre os valores de correlação da regressão e o índice de concordância de Willmott (d) foi calculado por meio da relação c=Rd. O desempenho (D) dos métodos foi classificado como: péssimo (0 < c ≤ 25%), ruim (25% < c ≤ 50%), regular (50% < c ≤ 75%), ótimo (75% < c ≤ 100%). Todas as análises foram realizadas utilizado o software R (R Core Team, 2015), por meio dos pacotes geoR e gstat.
RESULTADOS E DISCUSSÃO
O teste de Grubbs foi não-significativo para altura dominante (p-valor > 0,05), indicando ausência de valores extremos. Para a variável DAP, o teste foi significativo (p < 0,05), indicando como outlier o valor mínimo do conjunto de dados (9,93 cm), onde foi removido em seguida. A exclusão de outliers é indicada pois reduz a variação ao acaso, representada pelo efeito pepita, e pode elevar o índice de dependência espacial da variável (Mello et al., 2005b).
Os parâmetros de ajuste dos modelos de semivariância, além das estatísticas de ajuste e índice de dependência espacial, constam no Quadro 1. Em todos os modelos ajustados a altura dominante se apresentou com forte dependência espacial, sendo o modelo esférico o de melhor ajuste ao semivariograma experimental (Figura 1) utilizado na krigagem ordinária. Como este modelo apresentou o menor AIC, foi considerado o mais confiável entre os modelos candidatos.
Quadro 1 Efeito pepita ( C 0 ), contribuição (C), alcance (a(m)), erro médio reduzido ( ER ), desvio padrão dos erros reduzidos (Ser), critério de informação de Akaike (AIC) e índice de dependência espacial (IDE%) dos modelos teóricos de semivariância ajustados para a krigagem ordinária
| Modelo | 𝐂 𝟎 𝐂 𝐚(m) 𝐄𝐑Ser | AIC | IDE(%) | ||||
|---|---|---|---|---|---|---|---|
| Esférico | 0,14 | 14,03 | 571,77 | -0,00 | 1,00 | 1.063 | 100 |
| Exponencial | 0,00 | 14,35 | 329,71 | -0,00 | 1,00 | 1.072 | 100 |
| Gaussiano | 3,17 | 9,65 | 296,54 | -0,00 | 0,97 | 1.077 | 75 |
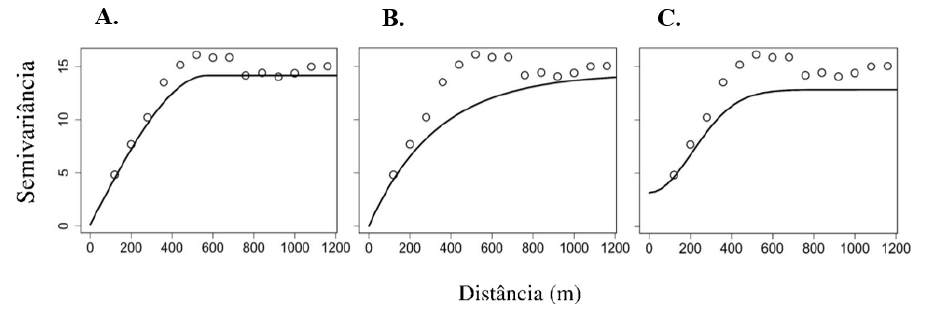
Figura 1 Modelos de semivariância teóricos esférico (A), exponencial (B) e gaussiano (C) ajustados ao semivariograma experimental unidirecional na análise geoestatística da variável altura dominante (Hd) em povoamento de eucalipto
Estes resultados retratam que a altura dominante é uma variável que tende a apresentar elevada estrutura de dependência espacial, conforme encontrado também por Mello et al. (2005b) e Guedes et al. (2015), avaliando o gênero Eucalyptus sp., e Pelissari et al. (2012), em estudos com Tectona grandis L. f. (teca). Mesmo não assumindo normalidade dos dados, a altura dominante apresentou, em geral, valores de ER próximos de zero, demonstrando que os resíduos convergem para um ponto central em sua distribuição. Assim, as estimativas para os pontos não amostrados apresentaram baixo nível de tendenciosidade.
O alcance de 571,77 m obtido pelo modelo esférico, demonstra uma maior distância em que a semivariância está estruturada e que a dependência espacial deve ser considerada. O alcance é um parâmetro importante, pois quanto mais elevado, maior é a área dos estratos considerados homogêneos e, sobretudo, permite a redução na intensidade amostral sem ônus na qualidade das estimativas espaciais em inventários futuros (Mello et al., 2005b; Lundgren et al., 2016). Além disso, é um parâmetro que indica a distância limite em que os interpoladores geoestatísticos geram estimativas robustas.
Na cokrigagem ordinária, o modelo esférico também foi o que apresentou melhor ajuste ao semivariograma cruzado experimental (Figura 2). Esse modelo permitiu um alcance de 608 m e índice de dependência espacial igual a 100%, permitindo associar pesos as unidades amostrais com maior índice de confiança associada.
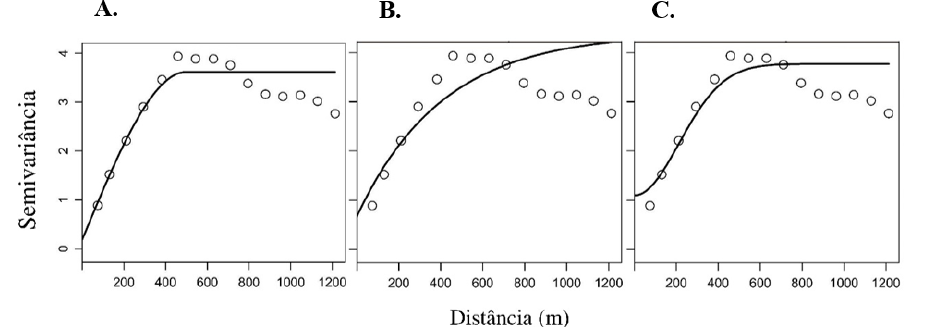
Figura 2 Modelos de semivariância teóricos esférico (A), exponencial (B) e gaussiano (C) ajustados ao semivariograma experimental cruzado na análise geoestatística da variável altura dominante (Hd) com a covariável diâmetro a 1,30 m do solo (DAP) em povoamento de eucalipto.
Na sequência, a altura média das árvores dominantes foi estimada nos locais não amostrados, a partir dos interpoladores geoestatísticos e determinísticos avaliados. No Quadro 2 estão apresentadas as estatísticas de precisão, exatidão e desempenho dos interpoladores espaciais.
Quadro 2 Erro médio reduzido ( ER ), desvio padrão dos erros reduzidos (ser), coeficiente de correlação de Pearson (r), índice de concordância de Willmott (d), índice de desempenho (c) e desempenho (D) da interpolação geoestatística e determinística da altura dominante em povoamento de eucalipto
| Interpolador | 𝐄𝐑Ser | r | d | 𝛃 𝟎 𝛃 𝟏c | D | |||
|---|---|---|---|---|---|---|---|---|
| KO | 0,0032 | 0,9465 | 0,8509 | 0,9127 | 6,6510 ns | 0,7217 ns | 0,7766 | Ótimo |
| CKO | 0,0027 | 1,3044 | 0,8610 | 0,9162 | 6,9454 ns | 0,7110 ns | 0,7888 | Ótimo |
| IQD | 0,0816 | 2,1001 | 0,8377 | 0,8797 | 10,0214 ns | 0,5828 ns | 0,7369 | Regular |
| PG | 0,0547 | 3,0640 | 0,6856 | 0,8123 | 6,3818 ns | 0,7345 ns | 0,5570 | Regular |
Em que KO = krigagem ordinária, CKO = cokrigagem ordinária; IQD = inverso do quadrado da distância; PG = polinômio global do 10º grau; ns = não-significativo.
Os valores de ER inferiores a 8,5%, para todos os métodos, são considerados baixos (Mello et al., 2005a). Isso está relacionado com a homogeneidade da variável no povoamento e a baixa variação aleatória no espaço, natural entre árvores dominantes do mesmo povoamento. Essa homogeneidade espacial corrobora o estudo feito por Guedes et al. (2015), em que a altura dominante demonstrou a menor variação em relação ao incremento médio anual e volume em plantios clonais de eucalipto.
Os métodos krigagem e cokrigagem apresentaram valores de ER e Ser mais próximos de zero e um, respectivamente, demonstrando a superioridade dos interpoladores geoestatísticos em predizer a altura dominante sem viés. Essa qualidade é inerente aos interpoladores geoestatísticos, cujas principais premissas são a variância mínima e a ausência de tendências nas estimativas (Mello et al., 2005a).
O desempenho da cokrigagem foi classificado como ótimo, indicando que o DAP eleva a confiabilidade nas estimativas espaciais da altura dominante. Avaliando o desempenho de métodos estatísticos e geoestatísticos na predição do volume em um povoamento de eucalipto, Lundgren et al. (2015), verificaram que o uso do DAP, como informação adicional na cokrigagem, também melhorou o desempenho nas estimativas espaciais, justificada também pela correlação forte (0,88) entre o diâmetro e volume. É valido ressaltar que a isotropia, condição em que a variável primária e secundária são mensuradas nas mesmas amostras (Yamamoto & Landim, 2013), concomitantemente com a correlação moderada (R=0,64) entre altura dominante e DAP, pode ter limitado o desempenho da cokrigagem em relação a krigagem.
A krigagem ordinária apresentou, também, ótimo desempenho em predizer a altura dominante na área analisada. Mesmo apresentado indicadores de desempenho (R = 0,8509 e d = 0,9127) pouco inferiores a cokrigagem ordinária, dentre todos os interpoladores analisados, foi a que gerou estimativas de menor tendência. Esse desempenho, é resultado da forte dependência espacial da altura dominante, que permitiu ponderar com robustez o nível de contribuição das amostras vizinhas nos locais não amostrados.
O inverso do quadrado da distância apresentou desempenho regular, com menores níveis de precisão e exatidão em relação aos métodos geoestatísticos. O ER encontrado indica uma tendência em superestimar a altura dominante, com maiores erros associados. O coeficiente de correlação de Pearson e índice de concordância de Willmott, para o inverso do quadrado da distância, foram próximos ao apresentado pelos métodos geoestatísticos, o que pode ser explicado pela intensidade amostral elevada (1.23%), homogeneidade da variável e distribuição sistemática das unidades amostrais.
Dentre todos os métodos testados, o polinômio global do 10° grau, de desempenho regular, estimou a altura dominante com menor precisão e exatidão. Esse interpolador determinístico é indicado para obtenção de informações de áreas extensas, em que a superfície apresenta informações cuja variabilidade é gradual (Negreiros et al., 2008). Mesmo apresentando baixa variação natural entre a altura das árvores dominantes, essa variação em nível local não permitiu estimativas confiáveis. Para a estratificação de uma superfície detalhada, os modelos polinomiais demandam de ordens maiores, ocasionando uma maior exposição a erros de predição. Em inventários florestais de cunho estratégico (Péllico Netto & Brena, 1997), geralmente aplicados em grandes áreas, o método pode apresentar melhor desempenho na espacialização de variáveis dendrométricas, em que o esforço amostral é menor (menor densidade de pontos).
Na Figura 3 estão os valores estimados de altura dominante em função dos valores observados em cada método, além dos coeficientes do ajuste da regressão linear simples.
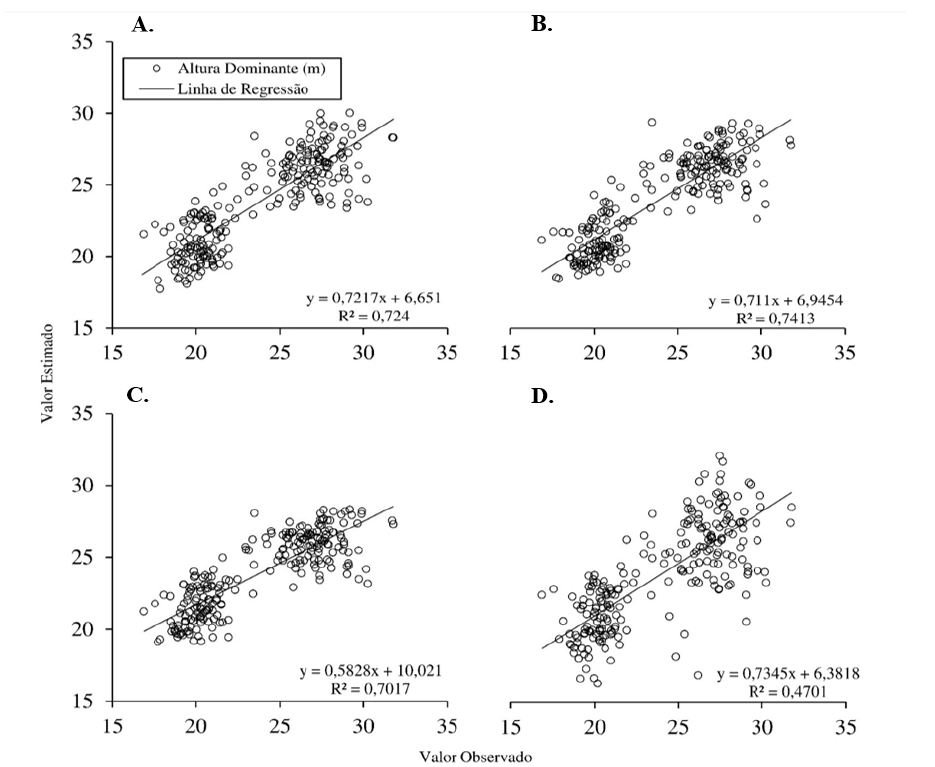
Figura 3 Valores preditos em função dos valores observados da altura dominante em povoamento de eucalipto pelos interpoladores espaciais krigagem ordinária (A), cokrigagem ordinária (B), inverso do quadrado da distância (C) e polinômio global do 10º grau (D).
Observa-se que os métodos geoestatatíticos foram superiores em produzir estimativas distribuídas em torno da linha de referência, seguido pelo inverso do quadrado da distância e polinômio global do 10º grau. O inverso do quadrado da distância apresentou o menor nível de exatidão, expresso por 𝛽 0 mais distante de zero (10,02) e 𝛽 1 de um (0,58). Apesar da inclinação mais perto do ideal ( 𝛽 0 = 0 e 𝛽 1 = 1) apresentada pelo polinômio global do 10º grau, a precisão desse modelo foi a menor dentre todos os interpoladores, conforme exibido pelo seu coeficiente de determinação (R² = 0,47). Este interpolador foi o que apresentou menor desempenho na predição dos valores.
Os mapas de predição de altura dominante para os métodos determinísticos e geoestatísticos estão apresentados na Figura 4.
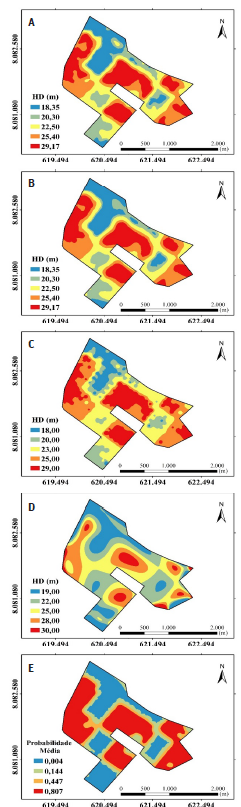
Figura 4 Espacialização da variável altura dominante em povoamento de eucalipto pelos interpoladores espaciais krigagem ordinária (A), cokrigagem ordinária (B), inverso do quadrado da distância (C), polinômio global do 10º grau (D) e da probabilidade associada a valores que excederam a média da variável pela krigagem indicatriz (E). Projeção UTM: Zona 23K - SIRGAS 2000.
O inverso do quadrado da distância, a krigagem e cokrigagem ordinária apresentaram estratos, em geral, muito semelhantes. No entanto, o mapa do inverso do quadrado da distância, apresentou o ruído conhecido como efeito mira ao redor das unidades amostrais, desvantagem desse interpolador (Mazzini & Schettini, 2009).
O mapa do polinômio global do 10º grau ilustrou o comportamento geral da altura dominante, mas com elevado erro de espacialização, decorrentes das características dessa interpolação. De acordo com Mazzini & Schettini (2009) o objetivo da regressão polinomial é descrever as tendências em larga-escala dos valores, e não prever os valores da variável dependente.
Os métodos geoestatísticos, pela possibilidade de utilizar a dependência espacial e gerar mapas com estratos definidos e precisos, demonstraram potencial elevado na caracterização precisa da capacidade produtiva da área. Além disso, a krigagem indicatriz permitiu a espacialização dos locais com maior probabilidade da altura dominante ser maior que a sua média (Figura 4E). A média espacial, definida como valor de corte, foi de 24,24 m. A krigagem indicatriz apresentou valores de ER e Ser igual a 0 e 1,04, respectivamente. Estes valores sugerem estimativas sem tendências associadas e confiabilidade na espacialização das probabilidades. Foram observadas quatro estratos indicando a probabilidade da altura dominante média, nesses locais, ser maior que a média espacial (Figura 4E). Essa infomação possui grande importância pois identifica zonas diferenciadas de manejo, e permite preliminarmente, direcionar prescrições silviculturais que maximizem a capacidade produtiva de cada estrato.
CONCLUSÕES
A altura média das árvores dominantes em povoamentos deeucalipto apresenta-se com forte estrutura de dependência espacial, sendo recomendada a utilização dos métodos geoestatísticos na sua espacialização.
A cokrigagem ordinária, utilizando o diâmetro como variável auxiliar, gera estimativas precisas e exatas, ampliando a acurácia no mapeamento da variabilidade espacial da altura dominante, também observada pela krigagem ordinária.
A krigagem indicatriz garante o mapeamento da probabilidade de uma determinada classe de altura dominante ocorrer, sendo essa uma informação primordial para o mapeamento do potencial produtivo em uma região e, consequentemente, do planejamento da rotação florestal.














