INTRODUCTION
Salinization has been identified as a major cause of soil degradation in countries located in the Mediterranean basin (European Commission, 2002). Assessments indicate that 1 to 4 million hectares of soils of the enlarged European Union, and mainly in the Mediterranean region, have moderate to high levels of degradation by salinization (Van Camp et al., 2004). The climatic and ecological conditions of the Mediterranean region, characterized by mild rainy winters and warm to hot dry summers, with high solar radiation and high evapotranspiration rates, favor salt accumulation in soils (Zalidis et al., 2002). Salts can accumulate in soils from both natural and anthropogenic sources. Natural sources include the process of mineral weathering where salts are gradually released and made soluble, salt deposition from rain, and upwards movement of groundwater due to capillary action that can bring salts from groundwater to surface soil. The anthropogenic sources include salts added through irrigation water and fertilization practices. The vulnerability to soil degradation of the Mediterranean region may worsen at increasing rates in the coming decades. The reasons for such vulnerability are the expected increase in irrigated areas, intensive farming and poor drainage, and also climate alterations (with intensified dry periods and temperature rise), and the increasing scarcity of good quality water (Bowyer et al., 2009; Riediger et al., 2014).
This study was carried out in Lezíria Grande de Vila Franca de Xira (Portugal), an important agricultural region of alluvial origin in the estuary of the river Tejo (1-2 m above sea level). This region presents primary salinization, due to the alluvial and marine origin of the soil, the tidal nature of the estuary and the existence of a saline water table (12-30 dS m-1 at 1-2 m depth). Lezíria also presents secondary salinization risks due to degradation of the irrigation water quality, especially in drought years, since the water is uptaken in a zone with tidal influence and increased probability of saline intrusion. A way to tackle soil salinization and/or sodicization phenomena in irrigated agriculture and particularly in regions with increased vulnerability is using a modelling approach. During the last decades, numerical models have been increasingly used to predict and to analyse water flow and solute transport in the unsaturated zone (Rubio and Poyatos, 2012). Hydrus-1D (Šimůnek et al., 2016) is one of the most widely used models based on the physical concepts of water flow and solute transport, that solve the Richards equation for water movement, and the advection-dispersion equation for solute transport. Modelling the subsurface water flow and salts dynamics in the vadose zone allows the understanding of the transport processes and the management of contamination risks. With such modelling in and below the root zone, one can further achieve the prediction of salinization risks and the implementation of better irrigation and fertilization practices (Gonçalves et al., 2006). The Hydrus software has been used for modelling and simulating outputs from irrigation and fertilization practices (Ramos et al., 2011).
In this study, the model Hydrus-1D was used to evaluate soil water and salt dynamics in an irrigated Fluvisol cultivated in a crop rotation of maize and annual ryegrass, and to predict irrigation-induced risks of soil salinization. The aims were: (i) to calibrate the Hydrus-1D model for predicting soil water flow and solute transport with observed field data and considering the presence of a saline water table, (ii) to predict future risks of soil salinization when irrigated with different water qualities using scenario analysis, (iii) to evaluate the salts dynamics in the soil profile explored by the roots in those scenarios, (iv) to perform a soil water and salt balance after both crop cycles and to evaluate the final levels of salinity in the soil at the end of the simulated period.
MATERIAL AND METHODS
Study area
The study area is located in Lezíria Grande de Vila Franca de Xira (Lezíria), approximately 25 km northeast of Lisbon, Portugal. The area is a peninsula that rises 1-2 m above the sea level and is located in the transition between the Tagus estuary and the Sorraia River as shown in Figure 1. Lezíria is an important agricultural area of about 13400 hectares with irrigation and drainage infrastructures for intensive crop production and pastures. This area of low elevation land is surrounded by protection dykes and is prone to shallow saline water tables arising from the estuarine tides. The climate is temperate with hot and dry summers, according to the Köppen classification. Regional climate measurements for the period from 1971 to 2000 show an average annual rainfall of 716 mm, which occurs mainly in winter, with a maximum in November (127.6 mm) and a minimum in July (2 mm). For the same period of 1971-2000, the average maximum temperature was 28.8 °C (August), and the average minimum temperature was 6.7 °C (January and February). The average annual aridity index for this period, calculated as the ratio between precipitation and potential evapotranspiration, was 0.5, corresponding to a dry subhumid type of climate (Portal do Clima, n.d.).
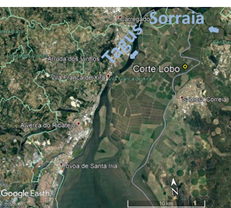
Figure 1 The study area of Corte Lobo located in Lezíria Grande de Vila Franca de Xira (Lisbon, Portugal).
The soils in Lezíria are from alluvial, fluvial and marine origin, typically clayey and homogeneous with fine to very fine texture. In the northern part of the Lezíria, where the experimental field of Corte Lobo is located (38° 57' 26.9''N 08°52' 17.5'' W), the soil is classified as Fluvisol (according to IUSS Working Group WRB, 2014). In Corte Lobo the soil presents a clay-loam texture (Table 1) and the subsoil layers, i.e. below 0.7 m depth, are classified as sodic according to Richards (1954), i.e. soils with an electrical conductivity of the soil saturated paste, ECe < 4.0 dS m-1, and the exchangeable sodium percentage, ESP ( 15.
Table 1 Soil physical and chemical characteristics at the study area in Lezíria
| Depth (cm) | 0-30 | 30-60 | 60-90 | 90-120 | 120-150 |
| Coarse sand (g Kg-1) | 1.45 | 1.49 | 1.06 | 0.63 | 0.74 |
| Fine sand (g Kg-1) | 15.80 | 10.31 | 5.51 | 2.96 | 3.27 |
| Silt (g Kg-1) | 47.40 | 42.26 | 42.49 | 44.77 | 45.06 |
| Clay (g Kg-1) | 35.36 | 45.94 | 50.95 | 51.63 | 50.94 |
| Texture | Silty-Clay-loam | Clay-loam | Clay-loam | Clay-loam | Clay-loam |
| pH (H2O) | 7.12 | 8.01 | 8.55 | 8.69 | 8.56 |
| ECe (dS m-1) | 1.85 | 2.87 | 2.97 | 3.01 | 3.86 |
| SAR (meq L-1)0.5 | 7.03 | 9.86 | 12.41 | 19.32 | 23.48 |
| ESP (%) | 7.99 | 8.92 | 11.37 | 14.60 | 15.52 |
| CEC (cmol(c) kg-1)c | 22.35 | 22.17 | 24.93 | 26.46 | 23.25 |
| Classification according to ECe and ESP (Richards, 1954)* | Nonsaline and nonsodic | Nonsaline and nonsodic | Nonsaline and nonsodic | Sodic | Sodic |
*Soils are classified as: nonsaline and nonsodic with an electrical conductivity of the soil saturated paste, ECe < 4.0 dS m-1 and the exchangeable sodium percentage, ESP < 15 and as sodic with an ECe < 4.0 dS m-1 and ESP ( 15.
Field measurements
In Corte Lobo, field measurements were performed during two growing seasons of maize (Zea mays L.) from sowing to harvest dates in two consecutive years (15/06/2017 to 12/10/2017 and 22/05/2018 to 9/10/2018). Annual ryegrass (Lolium multiflorum, Lam) was used as a winter crop. During the growing season, the electrical conductivity of the irrigation water (ECw) was 0.48 dS m-1 and when fertilizers were applied ECw was elevated to 4 dS m-1. Irrigation was made with a center pivot (10 mm/event) and a total of 3600 m3ha-1 was applied each year corresponding to 79% of the crop evapotranspiration (ETc) in 2017 and 76% of the ETc in 2018. The amount of irrigation water applied in both maize cycles resulted from the economic exploitation of this field by a farmer. Probably, this water-saving strategy was due to limited water availability in the region, since 2017 was a year of drought.
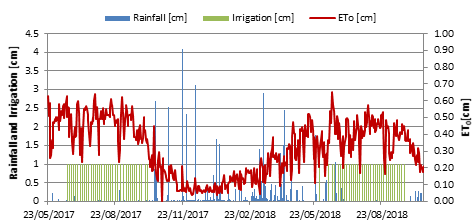
Figure 2 Rainfall, irrigation and reference evapotranspiration in Corte Lobo located in Lezíria (Portugal) during the study period.
Soil moisture (() was monitored using the gravimetric method, where the soil moisture content is expressed by weight as the ratio of the mass of water present to the dry weight of the soil sample. Soil samples were collected (two dates in 2017 and six in 2018) at five different depths in each 30 cm of soil and up to 150 cm depth. Soil salinity was monitored in those depths by measuring the electrical conductivity of the soil saturated paste (ECe in dS m−1) in the extract collected with suction filters according to the method described by Richards (1954).
Simulation Model
Simulations of soil water content and solute transport were performed using Hydrus-1D software package version 4. This model can numerically simulate one-dimensional water flow and solute transport in a variably-saturated porous media by solving the Richards (2), and the convection-dispersion equations CDE (Simůnek et al., 2016).
where θ is the volumetric water content (L3 L−3), t is the time (T), K is the hydraulic conductivity function (L T−1), h is soil water pressure head (L), z is the spatial coordinate (positive upward) (L), and S is the sink term accounting for root water uptake (L3L−3T−1). The model uses the van Genuchten-Mualem soil-hydraulic functions to parametrize the water retention curve θ(h) (Van Genuchten, 1980), given by equation (3). The hydraulic conductivity function as presented by Mualem (1976) is described by equation (4):
where θris the residual water content [L−3L−3], θsis the saturated water content [L−3L−3], h is the water pressure head [L], α [L−1], n and m are empirical parameters (m = 1 - (1/n)), Ks is the saturated hydraulic conductivity, l is a pore connectivity parameter, S e is the effective saturation, (0 ≤ S e ≤ 1), given by S e = (θ - θr)/(θs - θr). The Hydrus-1D model solves the advection-dispersion equations (CDE) for heat transfer and solute transport that also considers molecular diffusion (Ramos et al., 2011) given by the following equation (5):
where C is the solute concentration of the liquid phase [M L−3], D is the dispersion coefficient [L2 T−1], and v is the average pore water velocity [L T−1]. When ignoring molecular diffusion, the dispersion coefficient can be calculated by the product of v, average pore water velocity with λ, dispersivity (L) that is viewed as a material constant independent of the flow rate.
The sink term, S, in the Richards equation (eq. 2) is defined as the volume of water removed by plants from a unit volume of soil per unit of time (L3 L−3 T−1). It is calculated using the macroscopic approach by Feddes et al. (1978), where the potential root water uptake rate, corresponding to the potential transpiration rate (L T-1), is distributed over the root zone and reduced due to the presence of depth-varying water and osmotic stresses (Skaggs et al., 2006; Šimůnek and Hopmans, 2009). In this study, the Feddes model was considered as the water stress response function and parameters used for maize were: h1 = −15 cm, h2 = −30 cm, h3 = −325 to −600 cm, h4 = −8000 cm, available in Hydrus-1D database (Wesseling, 1991), where h1 corresponds to the pressure head below which roots start to extract water from the soil, and h3 is the value of the limiting pressure head below which roots can no longer extract water at the maximum rate. Water uptake is considered optimal between pressure heads h2 and h3, whereas for pressure heads between h1 and h2 water uptake decreases (or increases) linearly with pressure head. Water uptake becomes zero when the pressure head is below h4 or over h1. The osmotic effects of pore water salinity on root water uptake were considered by applying Maas’s (1990) threshold-slope function. Hydrus-1D has a database with threshold-slope salinity parameters for several crops based on Maas’s work. These threshold values were based on the electrical conductivity of the saturation extract (ECe) and were converted in EC of the soil water (ECsw) using the ratio ECsw/ECe = 2. For the maize crop, the database considers a slope (s) of 6% and a threshold value (ECt) of 3.40 dSm-1. In this study, the effects of water and salinity stresses were further assumed to be multiplicative (van Genüchten, 1987), enhancing those effects on root water uptake (Oster et al., 2012).
Model setup
Initial and boundary conditions
Simulations were performed in a 516 days period, considering 1.5 m soil profile composed with 5 layers in 30 cm depth increments. It was also considered the use of atmospheric boundary conditions (BC) with daily data of potential evaporation and transpiration rates, and the irrigation, rainfall, and concentration fluxes on the surface layer (Figure 2). Daily crop evapotranspiration rates (ETc) were calculated using the product of daily reference evapotranspiration rate (ETo) and the single crop coefficient (Kc) for the Mediterranean region (Allen et al., 1998). Kc is a crop coefficient accounting for both soil evaporation and crop transpiration. The Kc values used for maize were: 0.30 during the initial stage (during 27 days after sowing (DAS) in 2017 and 30 DAS in 2018), increasing from 0.30 to 1.20 during the vegetative stage (between 28 to 56 DAS in 2017 and 31 to 63 DAS in 2018), 1.20 for mid-season (between 57 to 96 DAS in 2017 and 64 to 113 DAS in 2018), and decreasing until 0.60 for late season crop stage (between 97 to 119 DAS in 2017 and 114 to 140 DAS in 2018). For annual ryegrass, the Kc values used were: 0.95 for the initial crop stage (during 12 DAS in 2017), and increasing until 1.05 (from 13 to 29 DAS in 2017), and 1.05 for mid and late-season stages (from 30 to 210 DAS in 2017). For maize, the leaf area index (LAI) curve used was obtained from Ramos et al. (2017) with a mean of 3.09 m2 m-2 (ranging between 0.01 - 6.33 m2 m-2). For annual ryegrass, it was used the estimated LAI curve from Lambert et al. (1999) with a mean value of 3.72 m2 m-2 (ranging between 0.01 - 4.20 m2 m-2). As required by Hydrus-1D, ETc daily values were divided into crop transpiration (T) and soil evaporation (E) rates. Both rates were estimated as a function of LAI and the corresponding Soil Cover Factor (SCF) to account for different stages of crop development, following the equations (6) proposed by Ritchie (1972):
Root depth was specified in the time-variable boundary conditions file increasing to a maximum depth of 50 cm for maize, and 30 cm for annual ryegrass. Variable pressure head was considered as lower boundary condition due to the presence of a groundwater table at the maximum and minimum depths of 2.6 and 1.3 m, respectively. Solute upper and lower boundary condition was assigned as a concentration flux. Initial soil water content and solute concentration were derived from field measurements to each soil layer. The EC of the groundwater table varied from 3 to 19 dS m-1 during the simulation period. To convert the ECe into total dissolved solids (TDS in gL-1) the following equation (7) was used (Richards, 1954):
TDS=(ECe×𝑘)/1000 [g L-1] (7)
Where: k = 640 if 0.1 < ECe ( 5 dSm-1 or k = 800 if ECe > 5 dSm-1
Soil hydraulic properties and solute parameters
The soil water retention curve, ( (h), was determined on 100 cm3 undisturbed soil samples in the laboratory using suction tables with sand for suctions below 100 cm, and a pressure plate apparatus for suctions above 1000 cm. Undisturbed soil samples (100 cm3) were collected at the beginning of the experiment on the different soil layers and were dried at 105 ºC to measure soil dry bulk density (( - g m-3). The saturated hydraulic conductivity (Ksat) was measured on 750 cm3 undisturbed soil samples at the depths 0-30 and 30-60 cm, using a constant head method. Measured water retention points and saturated hydraulic conductivity were parameterized using the van Genuchten equation that describes the volumetric soil water content, θ (L3L− 3), as a function of matric potential, ψ (L) (van Genuchten, 1980). The van Genuchten equation estimates the following set of parameters: residual and saturated water contents (θr and θs), saturated hydraulic conductivity (Ks) and empirical shape factors ((, n and l) by simultaneously optimizing the retention and conductivity parameters with the RETC computer program (van Genuchten et al., 1991). The soil hydraulic and solute transport parameters used as input to Hydrus -1D model are presented in Table 2.
Table 2 Values of volumetric water content (θr and θs), pore connectivity (l), saturated hydraulic conductivity (Ks), and shape parameters (α and n) for the different soil layers within the flow domain
| Depth (cm) | 0-30 | 30-60 | 60-90 | 90-120 | 120-150 |
|---|---|---|---|---|---|
| θr (m3 m-3) | 0.08† | 0.08† | 0.09† | 0.10† | 0.10† |
| θs (m3 m-3) | 0.50† | 0.51† | 0.51† | 0.52† | 0.58† |
| l | -1 | -1 | -1 | -1 | -1 |
| Bulk density (g cm-3) | 1.3* | 1.3* | 1.2* | 1.2* | 1.2* |
| Ks (cm d-1) | 115 | 125 | 125 | 140 | 180 |
| α | 0.032 | 0.032 | 0.028 | 0.027 | 0.027 |
| n | 1.25 | 1.25 | 1.24 | 1.22 | 1.22 |
θr, residual volumetric water content; θs, saturated volumetric water content; l, pore connectivity parameter, Ks, Saturated hydraulic conductivity; α and n, shape parameters.
† Measured properties in laboratory experiments: soil water retention curve parameterized with the van Genüchten equation
*Obtained as an average from 2 cylinders,
Statistical analysis
Field measurements of soil water content and total dissolved solids in soil water were compared with results from Hydrus-1D simulations using the mean error (ME) and root mean square error (RMSE). ME is given by equation (8), and describes the average of error in a set of data, meaning the difference between observations (Oi) and model predictions (Pi) in the units of a particular variable, with n being the number of observations:
RMSE is the square root of the mean square error in the units of a particular variable and is given by equation (9):
The coefficient of determination (R2) was also used (10) where Oi and Pi are the observed and predicted values at time i (i ¼ 1, 2…, n), and O and P are the mean observations and model predictions. ME and RMSE values close to zero indicate good model predictions. Values of R2 close to 1 indicate that the model explains well the variance of observations. This statistical analysis can evaluate the degree in which extend the RMSE value exceeds ME, usually a good indicator of the presence and extent of outliers, or the variance of the differences between the observed values (Legates and McCabe, 1999). The Percent bias (PBIAS) was used (11) to evaluate the average tendency of the simulated data to be larger or smaller than the observed (Gupta et al., 1999). It also measures over- and underestimation of bias and expresses it as a percentage. PBIAS can vary between negative and positive values, and by definition, PBIAS values close to zero indicate better model performance.
Simulation scenarios
Soil salinization risks were assessed using the model Hydrus-1D in a scenario analysis. In this analysis, it was considered the application of three irrigation water qualities: S1.5, S3, and S5, corresponding to an ECw of 1.5, 3, and 5 dS m-1, respectively. These scenarios were compared with the baseline conditions in Lezíria (B), i.e., considering an electrical conductivity of the irrigation water (ECw) of 0.48 dS m-1. When setting up the scenarios, several conditions were maintained identical to the baseline. It was considered the same period of 2 years (2017-2018), the same crop rotation of maize and annual ryegrass, and the same boundary conditions for soil water and salinity. It was considered in each maize irrigation cycle a total amount of 3600 m3 ha-1 with an average of 10 mm per irrigation event and scheduled as the baseline conditions. The three scenario analysis will help to understand the possible salinization risks of this Fluvisol in Lezíria. Such analysis becomes of particular interest when considering that in a scenario of climatic alterations, the availability and quality of water for irrigation may decrease due to saltwater intrusion in the upper Tagus estuary (Rodrigues et al., 2019). For both maize irrigation cycles, it was estimated a soil water balance with Hydrus-1D. In the three scenarios, it was evaluated the mean solute concentration in the root zone and performed a salt balance to compare the consequences of irrigating with different water qualities. The salt balance was performed after the crop cycle and at the end of the simulation period to evaluate the final levels of salinity in the soil.
RESULTS AND DISCUSSION
Model adjustment
Table 2 shows the calibrated values of α, n, and Ks. Figure 3 shows the measured and simulated θ during the study period. In the simulation period, there was good agreement between measured and simulated values of soil water content in Lezíria with a ME of -0.001 m3 m-3, RMSE = 0.019 m3 m-3 (ranging from 0.23 to 0.58 m3 m-3), PBIAS = -0.006 % and R2 = 0.94. Soil water content was slightly overestimated at 15 and 45 cm depth in the 2018 irrigation season. These soil layers near the soil surface are prone to have higher soil heterogeneity due to chiselling and irrigation practices and are also more susceptible to reflect the inter-daily variations dependent on the time step used for specifying boundary conditions in Hydrus (in this case is one day). As expected, during the irrigation periods ( increases, and between the end of the irrigation season (September) and the beginning of rainy seasons (October or November), ( gradually decreased allowing maize to be harvested. During the rainfall season, soil water content is dependent on rainfall events. In this study, in the rainfall season of 2017-2018, we observe an increase in soil water content. During the simulated period, it was noticeable that the presence of shallow groundwater influenced soil water content in deeper soil layers.
Figure 3 Measured (dots) and predicted (solid line) soil water content (() for the different soil layers in the simulation period with Hydrus-1D in Corte Lobo, Lezíria (Portugal) 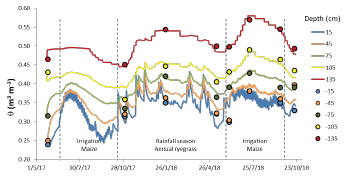
Figure 4 shows the fit between field observations and simulated values of the total dissolved solids in the soil (TDS) in the two irrigation cycles and considering a soil profile of 1.5 m. The adjustment was not as good for TDS as it was for ( as shown by an ME of 0.012 g L-1, RMSE = 0.208 g L-1 (ranging from 0.35 to 2.47 g L-1), PBIAS = 0.033% and R2 = 0.77.
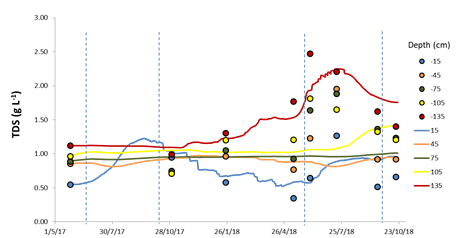
Figure 4 Measured (dots) and predicted (solid line) salinity (TDS) for the different soil layers in the simulation period with Hydrus-1D in Corte Lobo, Lezíria (Portugal).
In Figure 4 we observe that top and bottom soil layers were the ones showing better fit, and there is a generalized tendency of underestimating TDS in Hydrus-1D simulations. The soil depth of 75 cm is particularly unresponsive to irrigation events during the two years simulation period, probably due to the amount of water applied per irrigation event (10 mm) that is used by the crop and does not infiltrate to deeper soil layers. The overestimation of ( at 15 and 45 cm depth in the 2018 irrigation period, can lead to underestimating salinity in the same period as observed in Figure 4. For the model, the measured high TDS values in the deeper soil layers cannot be explained by the amount of irrigation water applied (3600 m3 ha-1 with an electrical conductivity of 0.48 dS m-1). Phogat et al. (2018) experienced similar difficulties when modelling salinity using Hydrus-2D and identified more difficulties in modelling salinity than soil water flow, especially for low values of water content. Several studies found better RMSE when modelling soil water content than when modelling salinity (Ramos et al., 2011; Slama et al., 2019). Roberts et al. (2009) found that Hydrus-2D underestimated salinity by approximately 1 dS m-1 using ECe. There are several possible causes for the underestimation of TDS in Lezíria by Hydrus-1D: soil spatial heterogeneity (also induced by chiselling practices), locally occurring geochemical processes, such as adsorption-desorption, and the alluvial and marine origin of the soils in this region. Also in Corte Lobo, the soil below 0.7 m depth is classified as sodic (according to Richards, 1954) and therefore facing the risk of degradation of their structure. Salts accumulation, and particularly Na+ and K+, often leads to clay dispersion, swelling, flocculation, and as a result reduces the soil hydraulic conductivity, infiltration rate, and soil water retention. The salt predictions by the model would be altered if the effects of salt accumulation on soil hydraulic properties were considered. Understanding that the adjustment of Hydrus-1D for salinity is far from perfect, we believe that such inaccuracy will not importantly affect the utility of this comparative study.
Salt concentration in the root zone resulting from irrigation water quality scenarios
Salts accumulation in the soil can occur as a consequence of irrigation water quality and is a process that increases over time. We evaluated the salinity level (TDS) in the Fluvisol layer of 15 cm in several scenarios with Hydrus-1D. At this soil layer near the surface, it is possible to evaluate the entry of salts due to the ECw, and as expected, with higher ECw the TDS increases (Figure 5). The salts build up over time, as shown in Figure 5, evidenced by the TDS increasing during the simulated period in the baseline and scenarios. At the end of the simulated period, TDS in the scenarios increased by 2, 3.8, and 5.9 times in S1.5, S3, and S5, respectively, when comparing with the baseline. TDS values indicated salt deposition at the end of the simulation period that is coincident with the end of the second irrigation cycle and excludes the 2018 rainfall season.
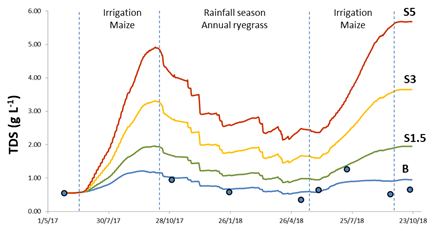
Figure 5 Total dissolved solids in the soil at 15 cm depth (observed in dots and predicted in solid line) for the baseline and scenarios of irrigation water quality in the simulation period with Hydrus-1D in Corte Lobo, Lezíria (Portugal).
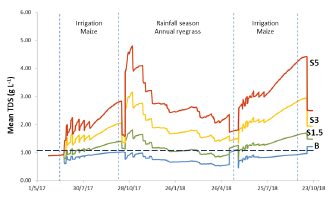
Figure 6 Mean solute concentration in the root zone for the baseline and scenarios of irrigation water quality in the simulation period with Hydrus-1D in Corte Lobo, Lezíria (Portugal). The threshold solute tolerance of maize is represented with the dashed horizontal line
In Figure 6 it is presented the mean solute concentration in the root zone of maize and annual ryegrass for the three ECw scenarios. These calculations were performed by Hydrus-1D considering the depth of 45 cm and once again, salinity builds up in the soil as ECw increases. Salts tend to accumulate initially at the soil surface and then are transported downwards and sideways depending on irrigation volumes and frequency, rainfall, evapotranspiration rates, and soil hydraulic properties. In the case of Hydrus-1D, it is only considered the downwards movement for salt transport and not lateral movements. The cyclical pattern is linked with salt accumulation during the crop cycles and lixiviation in the rainfall season, depending on the amount of irrigation, rainfall or evapotranspiration (Devitt et al., 2007). In Figures 5 and 6, we can observe the cyclical pattern that soil salinity is expected to exhibit. In the root zone, salts accumulate at the end of both irrigation cycles and it is observed a reduction in the mean concentration of solutes after the rainfall season (Figure 6). In the simulated scenarios of increasing ECw S3 and S5, the mean concentration of solutes in the root zone increased to levels above the threshold tolerance of maize, i.e., an ECe = 1.7 dSm-1 corresponding to TDS = 1.09 g L-1. Such values in the root zone became high enough to induce reductions in maize yield, but never exceeding the levels to obtain zero yields, i.e., an ECe = 10 dS m-1 corresponding to a TDS of 8 g L-1 (Ayers and Westcot, 1985; Mass, 1990; Steppuhn et al., 2005). While maize is considered moderately sensitive to salinity, annual ryegrass is moderately tolerant with a limit of tolerance of ECe = 6 dSm-1 that corresponds to approximately TDS= 3.84 g L-1 (FAO, 2002).
Water and salt balance in the root zone resulting from irrigation water quality scenarios
Table 3 shows the components of the soil water balance estimated with the Hydrus-1D model in both irrigation cycles of maize. The total water inputs in the two irrigation cycles were 470 mm in 2017 and 492 mm in 2018. In both crop seasons, the variation of the soil water storage was -9 mm and -2 mm in 2017 and 2018, respectively. In both crop seasons, maize did not register actual transpiration (Ta) reductions due to water stress. Simulation results of actual evaporation (Ea) for both irrigation cycles were 25% and 20% of total water inputs in 2017 and 2018, respectively. Capillary rise accounted for 24% of the total water inputs in 2017, and 20% in 2018. The total water balance error for both seasons was 2.4% and 1.2%, respectively.
Table 3 Water balance estimated with Hydrus-1D at the root zone for both irrigation cycles of maize in Corte Lobo, Lezíria (Portugal)
| Inputs | Outputs | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Net Rainfall R | Net Irrigation I | ( Soil storage S | Capillary rise CR | R+I+S+CR | Actual Evaporation Ea | Potential Transpiration Tp | Actual Transpiration Ta | Drainage D | E+Ta+D | Water balance error | |
| (mm) | (%) | ||||||||||
| 2017 Irrigation cycle (111 days) | 8 | 360 | -9 | 110 | 470 | 119 | 325 | 320 | 42 | 481 | 2.4 |
| 2018 Irrigation cycle (117 days) | 34 | 360 | -2 | 100 | 492 | 100 | 330 | 330 | 56 | 486 | 1.2 |
( Soil storage = (final - (initial
Water balance error = (inputs - outputs)/ inputs x 100
Salts accumulation or lixiviation in the root zone was evaluated by calculating the differences of solute concentration (TDS) at the beginning and end of each irrigation cycle, at the end of the rainfall season and the end of the simulation period (Table 4). As expected, the net salt concentration increased at the end of both irrigation cycles when compared with baseline simulation. After the rainfall season, the net value of TDS was negative meaning that salts lixiviated from the root zone. In this rainfall season has occurred 485 mm of precipitation distributed in 8 months (Oct-May). The rainfall-induced lixiviation was not sufficient to reduce salts to levels similar to the beginning of the first irrigation cycle. At the beginning of the second irrigation cycle (2018), the net value of TDS for scenarios S1.5, S3, and S5 increased 1.5, 2.2, and 3.2 times, respectively. At the end of the simulation period, we can observe the cumulative effect of salts build-up in the root zone in baseline and scenarios. For S1.5, S3, and S5 scenarios, salts accumulated in 1.77, 3.97, and 6.58 g L-1, corresponding to increases of 1.2, 2.7, and 4.5 times, respectively. In this study, the end of the simulation period does not include the subsequent rainfall season, and so, leaching of the salts from the root zone that could occur remains unknown. The importance of rainfall in root zone salinity dynamics was studied with Hydrus-1D by Phogat et al. (2018) to evaluate salinity risks to viticulture. In that study, simulations of seasonal average salinity indicated a remarkable increase of three or four times in the root zone salinity as rainfall-induced salt leaching was reduced to a great extent. Other studies also used the modelling approach to evaluate rainfall distribution role in determining soil seasonal salinity in the root zone (Isidoro and Grattan, 2011; Cucci et al., 2016).
Table 4 Salt balance expressed as TDS in the root zone (15-45 cm depth) in Corte Lobo, Lezíria (Portugal)
| TDS (g L-1) | B | S1.5 | S3 | S5 | ||
| Beginning of the 1st irrigation cycle (2017); t=26 | 1.43 | 1.43 | 1.44 | 1.43 | ||
| End of the 1st irrigation cycle (2017); t=137 | 2.08 | 2.87 | 4.24 | 5.87 | ||
| Net value 1st irrigation cycle | +0.65 | +1.44 | +2.80 | +4.44 | ||
| Beginning of the 2nd irrigation cycle (2018); t= 372 | 1.45 | 2.11 | 3.24 | 4.57 | ||
| Net value Rainfall season | -0.63 | -0.76 | -1.00 | -1.29 | ||
| End of the 2nd irrigation cycle (2018); t= 489 | 1.85 | 3.11 | 5.31 | 7.89 | ||
| Net value 2nd irrigation cycle | +0.40 | +1.00 | +2.07 | +3.32 | ||
| End of simulation period (2018); t=516 | 1.90 | 3.18 | 5.38 | 7.99 | ||
| Net value simulation period | +0.47 | +1.75 | +3.94 | +6.56 | ||
TDS, total dissolved solids in the soil; TDS Net value = TDSfinal - TDSinitial ; Influx (+); Efflux (-)
A way to control the increased root zone salinity above the crop threshold is by adopting an appropriate leaching fraction. In the case of this study, increasing the amount of water applied per irrigation cycle (3600 m3 ha-1) or irrigation event (10 mm). Although, a high leaching fraction may be advisable in this region, in drought years the amount of water available for irrigation is limited, and soluble salts that are leached out from root zone may re-enter in response to dynamic evaporative fluxes at the soil surface. In alternative, these salts can be leached deeper into the soil and may enter the river system via groundwater, which may be hydraulically connected (Cook et al., 2004).
CONCLUSIONS
In this study, we use a numerical model Hydrus-1D to evaluate soil water and salt dynamics in an irrigated Fluvisol and to evaluate future water-related salinity risks in response to different irrigation water qualities. Hydrus-1D successfully simulated soil water content and TDS. The model showed a better fit when simulating soil water content (RMSE = 0.019 m3 m-3 and R2= 0.94) than TDS (RMSE = 0.208 g L-1 and R2 = 0.77). In the baseline simulation, the irrigation-induced salinity risks were low. The scenario analysis strongly suggests that salinity risks increase when irrigation occurs with water of 3 and 5 dS m-1 (scenarios S3 and S5). In both scenarios, salts concentration in the root zone increases, 2.7 and 4.5 times when compared to baseline, to levels above the threshold tolerance of maize, probably inducing yield reductions with the associated economic losses and the salinity related environmental risks. Scenarios S3 and S5 also indicate salts accumulation in the root zone as rainfall-induced leaching was not sufficient to reduce to levels below the crop threshold. These predictions can be aggravated in drought years, where less rainfall occurs, and the seasonal-salinity increases salts build-up in the soil due to irrigation. In Lezíria, there are secondary salinization risks due to possible degradation of irrigation water quality, since the water is uptaken in a zone with tidal influence and increased probability of saline intrusion that can restrict the application of the leaching water fraction. In such sensitive regions, managing irrigation and monitoring soil seasonal salinity dynamics is of greater importance. Simulation of irrigation-induced risks using Hydrus-1D constitutes a very useful tool in planning and managing irrigation, and for predicting soil salinity risks.














