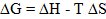INTRODUÇÃO
O quiabo (Abelmoschus esculentus (L.) Moench), é um vegetal consumido mundialmente, principalmente em regiões subtropicais e tropicais, contendo em sua composição proteínas, vitaminas, cálcio, ferro, potássio, magnésio, sódio, polifenóis e outros antioxidantes (Sabitha et al., 2012; Hussain et al., 2016; Kpodo et al., 2017). Contém teores apreciáveis de pectina e lignina, polissacarídeos hidrofílicos que em contato com a água formam uma solução de aspecto viscoso, que constitui um hidrocoloide (Khathuriya et al., 2015; Kpodo et al., 2018).
É colhido quando está parcialmente desenvolvido e fisiologicamente imaturo, apresentando uma vida de prateleira curta e alta perecibilidade, uma vez que o seu metabolismo respiratório continua ativo, com transformações químicas que ocorrem até que chegue ou ultrapasse a fase de amadurecimento (Santos et al., 2019a). A perda de valor comercial e desinteresse por parte do consumidor requerem o uso de medidas e técnicas que possam aumentar a vida útil, permitindo a manutenção da qualidade em condições de transporte e armazenamento.
Uma das formas mais efetivas de se reduzir o desperdício de produtos agrícolas em geral é por meio da secagem. A secagem é uma operação unitária de retirada de água do material por evaporação ou sublimação, mediante aplicação de calor em condições controladas, que faz decrescer a atividade de água, permitindo minimizar a deterioração causada pelas reações microbiológicas, químicas e enzimáticas. É realizada como uma transferência de calor que tem por objetivo a vaporização do líquido e a transferência de massa do líquido ou vapor presente no interior do material para a atmosfera, na forma de vapor (Tadini et al., 2016). A redução do teor de água faz com que o produto tenha maior estabilidade, maior vida útil, redução do peso e facilidade no transporte (Karam et al., 2016).
Por ser um processo que na maioria dos métodos utiliza o calor para promover a remoção de água, e que depende da composição e da matriz estrutural das matérias-primas, a máxima precisão para se descrever o comportamento destas quando submetidas a secagem requer estudos dedicados, com testes experimentais que são bem ajustados por modelos citados em literatura. A determinação da cinética de secagem e das propriedades termodinâmicas fornecem informações imprescindíveis para a execução do processo com a máxima eficiência. Ante o exposto, objetivou-se secar quiabo em fatias nas temperaturas de 50, 60, 70, 80 °C, ajustar modelos matemáticos aos dados experimentais e determinar os coeficientes de difusão, a energia de ativação e as propriedades termodinâmicas envolvidas.
MATERIAL E MÉTODOS
Matéria-prima
A matéria-prima utilizada foram quiabos (Abelmoschus esculentus (L.) Moench) quinados do subgrupo verde, da variedade Santa Cruz, em estádio de maturação verde, proveniente do município de Caturité, Estado da Paraíba, Brasil (latitude: 7° 25' 12'' S, longitude 36° 01' 37'' O, altitude 405 m).
Os quiabos foram transportados ao laboratório, selecionados manualmente de forma a eliminar os que apresentavam danos físicos ou estádio de maturação indesejado; em seguida, foram submetidos a uma lavagem em água corrente, sanitização em água clorada (50 ppm) por 15 min e, posteriormente, enxague em água corrente.
Cinética de secagem
Para a realização das secagens os quiabos foram cortados em fatias com espessura padronizada de 2 mm (Figura 1). Em seguida, as amostras eram colocadas em bandejas de aço inoxidável e submetidas à secagem em estufa com circulação forçada de ar, nas temperaturas de 50, 60, 70 e 80 °C, realizando-se pesagens em intervalos regulares até se constatar o equilíbrio higroscópico, identificado pela massa constante entre pesagens, determinando-se assim os dados da cinética de secagem, obtidos em triplicata.
No final das secagens foram determinadas as massas secas e calculados os teores de água. Com os dados experimentais calculou-se os valores da razão do teor de água (Equação 1).
Onde: RX - razão do teor de água do produto, adimensional; X - teor de água do produto em determinado tempo, % base seca; Xi - teor de água inicial do produto, % base seca; Xe - teor de água de equilíbrio do produto, % base seca.
Os dados das cinéticas de secagem dos quiabos, representadas pela razão do teor de água em função do tempo de secagem, foram assim obtidos, e os modelos matemáticos (Quadro 1) de Aproximação da difusão, Henderson e Pabis, Logarítmico, Midilli, Newton, Page e Thompson foram ajustados aos dados experimentais.
Quadro 1 Modelos matemáticos utilizados para estimar as curvas de cinética de secagem do quiabo
| Designação do modelo Matemático | Modelo | Equação |
|---|---|---|
| Aproximação da difusão | (2) | |
| Henderson e Pabis | (3) | |
| Logarítmico | (4) | |
| Midilli | (5) | |
| Newton | (6) | |
| Page | (7) | |
| Thompson | (8) |
RX - Razão do teor de água (adimensional), a, b, c, k, n - Constantes dos modelos, t - tempo (min)
Para aplicação dos ajustes matemáticos dos modelos aos dados experimentais foi utilizado o programa computacional Statistica 7.0, por meio de análise de regressão não linear, utilizando o método de estimativa Quasi-Newton. Para avaliar a qualidade do ajuste dos modelos aos dados experimentais, foram utilizados como critérios a análise do coeficiente de determinação (R²), do desvio quadrático médio (DQM) (Equação 9) e do qui-quadrado (χ2) (Equação 10).
Onde: DQM - desvio quadrático médio; RXpred - razão do teor de água predito pelo modelo, adimensional; RXexp - razão do teor de água experimental, adimensional; n - número de observações.
Onde: (2 - qui-quadrado; RXpred - razão de teor de água predita pelo modelo; RXexp - razão de teor de água experimental; N - número de observações; n - número de constantes do modelo
Os coeficientes de difusão efetiva (Def) do quiabo para as temperaturas de secagem de 50, 60, 70 e 80 °C foram calculados baseada na teoria da difusão líquida, representada pela equação que é a solução analítica da segunda lei de Fick, considerando-se a forma geométrica do produto como aproximada de uma placa plana e com aproximação de sete termos (n = 7), de acordo com Equação 11.
Onde: RX - razão do teor de água, adimensional; n - números de termos da equação; Def - difusividade efetiva (m² s-¹); L - espessura (m); t - tempo (s).
Para avaliar a influência da temperatura de secagem sobre o coeficiente de difusão efetivo (Def), os dados foram ajustados à equação do tipo Arrhenius (Equação 12).
Onde: Def - coeficiente de difusão efetivo (m2 s-1); Def0 - fator pré exponencial (m2 s-1); Ea - energia de ativação (kJ mol-1); R - constante universal dos gases, 0,008314 kJ mol-1 K-1; T - temperatura absoluta (K).
Propriedades termodinâmicas
As propriedades termodinâmicas do processo de secagem do quiabo em fatias determinadas foram a entalpia, entropia e a energia livre de Gibbs, de acordo com as Equações 13, 14 e 15, respectivamente (Corrêa et al., 2012).
Onde: ∆H - variação da entalpia (J mol-1); Ea - energia de ativação (J mol-1); R - constante universal dos gases, 8,314 J mol-1 K-1; T - temperatura absoluta (K); ∆S - variação da entropia (J mol-1 K-1); Kb - constante de Boltzmann, 1,38 x 10-26 J K-1; hp - constante de Planck, 6,626 × 10-37 J s; ∆G - variação de energia livre de Gibbs (J mol-1).
RESULTADOS E DISCUSSÃO
Os parâmetros dos modelos matemáticos (Quadro 2) ajustados aos dados experimentais das cinéticas de secagem dos quiabos em fatias, demostram que todos os modelos matemáticos proporcionaram bons ajustes, com coeficientes de determinação (R²) superiores a 0,98, desvios quadráticos médios (DQM) e qui-quadrado (χ²) inferiores a 0,068 e 0,0051, respectivamente. Dentre todos, o modelo de Midilli apresentou os maiores coeficientes de determinação (R² > 0,9990) e os menores desvios quadráticos médios (DQM < 0,013) e qui-quadrado (χ² < 0,0003) nas condições estudadas.
Quadro 2 Parâmetros obtidos, coeficientes de determinação (R²), desvios quadráticos médios (DQM) e qui-quadrado (χ²) dos modelos matemáticos ajustados aos dados da cinética de secagem do quiabo
| Modelo | T | Parâmetros | R2 | DQM | χ² | ||||
|---|---|---|---|---|---|---|---|---|---|
| (°C) | a | b | c | k | n | ||||
| Aproximação da difusão | 50 | -13,2651 | 0,9495 | - | 0,0099 | - | 0,9996 | 0,0097 | 0,0001 |
| 60 | -19,3196 | 0,9949 | - | 0,0144 | - | 0,9996 | 0,0104 | 0,0001 | |
| 70 | -95,0282 | 0,9915 | - | 0,0186 | - | 0,9989 | 0,0169 | 0,0003 | |
| 80 | -54,9894 | 0,9841 | - | 0,0252 | - | 0,9990 | 0,0163 | 0,0003 | |
| Henderson e Pabis | 50 | 1,0609 | - | - | 0,0056 | - | 0,9961 | 0,0320 | 0,0011 |
| 60 | 1,0707 | - | - | 0,0080 | - | 0,9951 | 0,0361 | 0,0014 | |
| 70 | 1,0826 | - | 0,0101 | - | 0,9930 | 0,0433 | 0,0020 | ||
| 80 | 1,0941 | - | - | 0,0132 | - | 0,9913 | 0,0483 | 0,0020 | |
| Logarítmico | 50 | 1,1173 | - | -0,0724 | 0,0048 | - | 0,9981 | 0,0224 | 0,0005 |
| 60 | 1,1219 | - | -0,0664 | 0,0070 | - | 0,9971 | 0,0278 | 0,0009 | |
| 70 | 1,1371 | - | -0,0710 | 0,0088 | - | 0,9955 | 0,0346 | 0,0013 | |
| 80 | 1,1594 | - | -0,0847 | 0,0111 | - | 0,9947 | 0,0380 | 0,0017 | |
| Midilli | 50 | 0,9944 | -0,0002 | - | 0,0013 | 1,2553 | 0,9998 | 0,0080 | 0,0001 |
| 60 | 0,9967 | -0,0003 | - | 0,0015 | 1,2812 | 0,9997 | 0,0092 | 0,0001 | |
| 70 | 0,9852 | -0,0003 | - | 0,0016 | 1,3932 | 0,9994 | 0,0126 | 0,0002 | |
| 80 | 0,9877 | -0,0003 | - | 0,0019 | 1,4578 | 0,9996 | 0,0103 | 0,0001 | |
| Newton | 50 | - | - | - | 0,0052 | - | 0,9932 | 0,0420 | 0,0018 |
| 60 | - | - | - | 0,0073 | - | 0,9915 | 0,0474 | 0,0023 | |
| 70 | - | - | - | 0,0091 | - | 0,9885 | 0,0553 | 0,0032 | |
| 80 | - | - | - | 0,0118 | - | 0,9857 | 0,0621 | 0,0040 | |
| Page | 50 | - | - | - | 0,0013 | 1,2651 | 0,9996 | 0,0098 | 0,0001 |
| 60 | - | - | - | 0,0017 | 1,3093 | 0,9996 | 0,0098 | 0,0001 | |
| 70 | - | - | - | 0,0017 | 1,3632 | 0,9992 | 0,0147 | 0,0002 | |
| 80 | - | - | - | 0,0018 | 1,4386 | 0,9995 | 0,0122 | 0,0002 | |
| Thompson | 50 | -12,1059 | 0,7655 | - | - | - | 0,9928 | 0,0439 | 0,0020 |
| 60 | -31,2806 | 1,4854 | - | - | - | 0,9913 | 0,0478 | 0,0024 | |
| 70 | -46,0888 | 2,0621 | - | - | - | 0,9884 | 0,0555 | 0,0033 | |
| 80 | -38,8716 | 0,6914 | - | - | - | 0,9829 | 0,0678 | 0,0050 | |
Diversos trabalhos abordando cinética de secagem de produtos agrícolas tem reportado o modelo de Midilli como o que resultou nos melhores ajustes, entre eles Doymaz e Medine (2016), ao estudarem a cinética de secagem de brócolis (Brassica oleracea) em fatias em secador convectivo nas temperaturas de 45, 55, 65 e 75 °C com velocidade de ar de 2,0 m/s; Silva et al. (2017), ao desidratarem cenouras nas temperaturas de 50, 60, 70 e 80 °C em estufa com circulação forçada de ar; Baptestini et al. (2017) na secagem de fatias de banana (cv. Prata) em quatro diferentes estádios de maturação nas temperaturas de 65, 75, 85 e 95 °C; e Santos et al. (2019b) na desidratação de fatias de acuri (Attalea phalerata Mart. ex Spreng.) em estufa com circulação de ar nas temperaturas de 60, 70, 80 e 90 °C, que também obtiveram excelentes ajustes com o modelo de Midilli.
O parâmetro k, dos modelos avaliados, que representa a constante da taxa de secagem, aumentou com o acréscimo da temperatura. Esse parâmetro representa o efeito das condições externas de secagem, o qual tendeu a aumentar com a elevação da temperatura do ar (Goneli et al., 2011). Nascimento et al. (2015), ao estudarem a secagem de vagens de algaroba (Prosopis juliflora SW) nas temperaturas de 60, 70 e 80 °C, reportaram que o aumento da temperatura de secagem resultou no aumento da constante k nos modelos utilizados.
Constata-se que houve aumento do parâmetro n dos modelos de Midilli e Page com o aumento da temperatura de secagem. O parâmetro n provê um efeito de moderação do tempo e corrige os prováveis erros resultantes da negligência da resistência interna para a transferência de água (Perez et al., 2013). Comportamento semelhante foi reportado por Reis et al. (2015) ao secarem pimenta da variedade bico (Capsicum chinense) em temperaturas de 40, 50 e 60 °C e velocidade do ar de secagem de 1,0; 1,5 e 2,0 m/s. As demais contantes dos modelos testados não possuem significado físico, de forma que suas variações se devem aos ajustes matemáticos, não tendo relação com o fenômeno de secagem, uma vez que os modelos utilizados são semiempíricos (Midilli et al., 2002).
Apresenta-se na Figura 2 a relação entre os valores da razão do teor de água experimentais e preditos (Figura 2A) e as curvas experimentais das cinéticas de secagem do quiabo (Figura 2B) nas temperaturas de 50, 60, 70 e 80 °C, com ajustes com o modelo de Midilli, utilizado por apresentar os melhores ajustes.
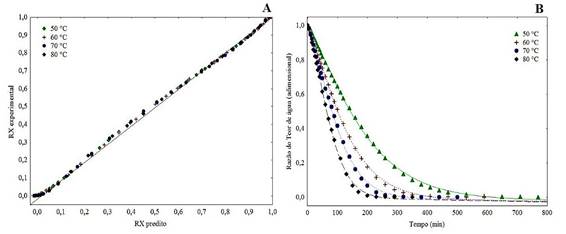
Figura 2 Relação entre os valores experimentais e preditos do teor de água (A); Curvas de cinética de secagem (B) do quiabo em fatias nas temperaturas de 50, 60, 70 e 80 °C ajustadas pelo modelo de Midilli.
Na Figura 2A observa-se a proximidade entre os valores experimentais e a curva representando os valores preditos pelo modelo, com valores praticamente coincidentes em razões de teor de água entre zero e 0,2 e acima de 0,7, demonstrando o correlacionamento positivo entre o comportamento das amostras na secagem e a predição do modelo, conforme os bons valores dos parâmetros R², DQM e χ2.
Nas curvas de cinética de secagem (Figura 2B) verifica-se, pelo distanciamento entre as curvas, um maior efeito do aumento de temperatura entre 50 e 60 °C do que os incrementos de 10 °C a partir da temperatura de 60 °C, correspondentes a 70 e 80 °C que aparentam coeficientes angulares mais aproximados até os primeiros 150 minutos de secagem. Os tempos de secagem foram de 770, 590, 500 e 350 minutos, com teores de água de equilíbrio de 8,45; 8,04; 5,27 e 5,14% bu, para as temperaturas de 50, 60, 70 e 80 °C respectivamente, com uma redução de 54,5% no tempo de desidratação da menor para a maior temperatura. Tempos mais curtos em temperaturas mais altas são consequência do aumento da taxa de transferência de calor para o interior do produto, provocando o aumento da taxa de remoção de água (Herman et al., 2018).
Wankhade et al. (2013) ao desidratarem o quiabo em fatias de 5 mm de espessura nas temperaturas de 40 a 90 °C verificaram uma perda do teor de água mais rápida no início da secagem, havendo redução no tempo de desidratação de 20% da menor para a maior temperatura; Afolabi e Agarry (2014) ao avaliarem a secagem em estufa de quiabo em fatias com espessuras de 10 a 20 mm, nas temperaturas de 50 a 70 °C, verificaram um tempo de secagem superior ao do presente estudo, variando de 720 a 1140 minutos, respectivamente; Famurewa e Olumofin (2015) ao estudarem a secagem do quiabo na espessura de 2 mm, nas temperaturas de 40, 50 e 60 °C, obtiveram teores de águas de equilíbrio de 13,00; 12,5 e 10% b.u, respectivamente.
Apresenta-se no Quadro 3 os coeficientes de difusão efetiva (Def), estimados com o modelo Fick, da secagem do quiabo nas temperaturas de 50 a 80 °C, com respectivos coeficientes de determinação. Os coeficientes de determinação (R2) foram superiores a 0,903, demonstrando que o modelo de Fick para uma placa plana, ajustou-se aos dados experimentais satisfatoriamente.
Quadro 3 Valores médios da difusividade efetiva (Def) obtidos na secagem do quiabo nas temperaturas de 50, 60, 70 e 80 °C e respectivos coeficientes de determinação (R2)
| Temperatura °C | Def (x 10-11 m² s-1) | R² |
|---|---|---|
| 50 | 2,60 | 0,9257 |
| 60 | 3,67 | 0,9204 |
| 70 | 4,63 | 0,9135 |
| 80 | 6,03 | 0,9046 |
Verifica-se o aumento da difusividade com a elevação da temperatura, representando a elevação da velocidade com que a água migra do interior para a superfície do produto, de forma que com o aumento da temperatura esse processo ocorre com maior rapidez. Segundo Goneli et al. (2014) a viscosidade da água diminui com o aumento da temperatura, favorecendo o movimento desta no interior do produto e deste para o ar de secagem, como consequência do aumento da difusão da água. Gupta e Alam (2014) explicaram que com o incremento da temperatura a difusividade efetiva também aumenta devido ao aumento da pressão de vapor dentro da amostra.
A magnitude dos coeficientes de difusão efetiva obtidos nos quiabos variou entre 2,60 x 10-11 e 6,03 x 10-11 m2 s-1. Segundo Madamba (2003) os valores do coeficiente de difusão efetiva para produtos alimentícios encontram-se dentro de uma faixa de 10-11 a 10-9 m2 s-1. Valores inferiores de Def foram encontrados por Doymaz (2005) ao estudarem a secagem do quiabo em secador convectivo nas temperaturas de 50 a 70 °C, em que verificaram valores de 4,27 x 10-10 a 1,30 x 10-9 m2 s-1, respectivamente; Sobukola (2009) determinaram para fatias de quiabos com 2 mm nas temperaturas de 50 °C valor de 7,13 x 10-9 m2 s-1, em 60 °C de 7,36 x 10-9 m2 s-1 e em 70 °C de 0,12 x 10-9 m2 s-1; e Afolabi e Agarry (2014), na secagem do quiabo em fatias com espessura de 20 mm, nas temperaturas de 50, 60 e 70 °C, verificaram valores de 3,29; 3,86 e 4,76 x 10-10, respectivamente.
A energia de ativação para a difusão liquida do quiabo foi de 26,12 kJ mol-1, valor que se encontra na faixa dos reportados para produtos agrícolas, os quais variam de 12,7 a 110 kJ mol-1 (Zogzas et al., 1996). A energia de ativação corresponde a barreira que deve ser ultrapassada para que o processo de difusão possa ser desencadeado, constituindo-se na energia mínima necessária para que as moléculas de água iniciem o movimento de dentro para fora do produto (Kashaninejad et al., 2007). Nos processos de secagem, quanto menor for a energia de ativação maior será a difusividade de água, isto é, mais baixa será a energia necessária para transformar a água em vapor (Corrêa et al., 2010). Valores superiores foram reportados por Doymaz e Medine (2016) na secagem de fatias de brócolis em secador convectivo, nas temperaturas de 45, 55, 65 e 75 °C, em que reportaram para o material sem tratamento o valor de 35,41 kJ mol-1. As variações na energia de ativação entre os diversos trabalhos é justificada pela diversidade das características físicas e biológicas dos produtos de origem agrícola (Martins et al., 2015).
Propriedades Termodinâmicas
No Quadro 4 são apresentados os valores das propriedades termodinâmicas variação de entalpia, entropia e de energia livre de Gibbs determinadas no processo de secagem do quiabo nas temperaturas de 50 a 80 °C.
Quadro 4 Valores médios da variação de entalpia (∆H), entropia (∆S) e energia livre de Gibbs (∆G) determinadas no processo de secagem do quiabo nas temperaturas de 50, 60, 70 e 80 °C
| Temperatura °C | ∆H (kJ mol-1) | ∆S (kJ mol-1 K-1) | ∆G (kJ mol-1) |
|---|---|---|---|
| 50 | 23,43 | -0,3672 | 142,09 |
| 60 | 23,35 | -0,3674 | 145,76 |
| 70 | 23,27 | -0,3677 | 149,44 |
| 80 | 23,18 | -0,3679 | 153,12 |
Os valores da variação de entalpia foram reduzidos de forma inversamente proporcional ao aumento de temperatura, com variações percentualmente pequenas, mas de maneira gradual e consistente. Resende et al. (2017) afirmaram que a energia necessária para a retirada da água do produto, que na secagem ocorre por difusão, é composta pela entalpia de vaporização da água livre e a entalpia de vaporização da água no produto ou calor isostérico. Com o aumento da temperatura e consequente aumento da pressão parcial de vapor da água no interior do material ocorre redução na entalpia de vaporização da água livre, de forma que no balanço final, com a elevação da temperatura do ar de secagem ocorre redução na entalpia (Araujo et al., 2017). Comportamento semelhante foi reportado por Silva et al. (2017) na secagem de cenouras em estufa com circulação de ar, nas temperaturas de desidratação de 50, 60, 70 e 80 °C, cujos valores de variação de entalpia apresentaram redução de 33,83 para 33,59 kJ mol-1.
A variação de entropia comportou-se de forma similar à entalpia, com valores sendo reduzidos com o acréscimo da temperatura de secagem. Com a elevação da temperatura do ar de secagem e consequente aumento na pressão parcial de vapor da água no produto, também ocorre aumento na excitação das moléculas de água e redução da viscosidade, fatores que combinados propiciam o aumento da velocidade do processo de difusão de água e redução da entropia no processo (Silva et al., 2016). Segundo Moreira et al. (2008), os valores negativos de entropia são atribuídos à existência de adsorção química e/ou modificações estruturais do adsorvente.
A variação de energia livre de Gibbs apresentou valores positivos, indicando que o processo é não espontâneo, sendo, portanto, necessário fornecer energia térmica para que possa ocorrer (Silva et al., 2016). A energia livre de Gibbs é uma função termodinâmica responsável por quantificar a máxima energia liberada em um processo sendo que, em condições de temperatura e pressão constantes, essa energia pode servir de indicativo quanto ao trabalho útil realizado e o seu valor positivo é explicado por uma adição de energia que envolve o produto para a ocorrência da mudança de fase (líquido para vapor), onde no caso de secagem não existe reação química, o que torna essa operação não espontânea nessas condições (Araujo et al., 2017).
Observou-se que houve aumento da energia livre de Gibbs com o aumento da temperatura de secagem, comportamento reportado em outros estudos: como na secagem de folhas de timbó nas temperaturas de 40, 50, 60 e 70 °C, com valores de 140,10 kJ mol-1, 142,07 kJ mol-1, 144,03 kJ mol-1 e 145,99 J mol-1 respectivamente (Martins et al., 2015); em fatias de alho desidratadas nas temperaturas de 40 a 60 °C, encontraram valores de 100,43 a 103,96 kJ mol-1 (Cagnin et al., 2017); e em grãos de girassol (Helianthus annuus), secados nas temperaturas de 40, 60, 80 e 100 °C, com valores de 93,52; 97,99; 102,46 e 106,95 kJ mol-1, respectivamente (Carvalho et al., 2018).
CONCLUSÕES
O modelo de Midilli resultou nos melhores ajustes da cinética de secagem de quiabo nas temperaturas de 50 a 80 °C, seguido pelo modelo de Page; Os quiabos secados em fatias apresentaram coeficientes de difusão efetivos na ordem de 10-11 m2 s-1 e energia de ativação de 26,12 kJ mol-1;
As propriedades termodinâmicas foram afetadas pela temperatura de secagem, com reduções da variação de entalpia e entropia, e aumento da variação de energia de Gibbs, indicando um processo endergônico não espontâneo, requerendo energia para sua realização.