Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Similares em
SciELO
Similares em
SciELO
Compartilhar
Revista Portuguesa de Educação
versão impressa ISSN 0871-9187
Rev. Port. de Educação vol.24 no.2 Braga 2011
Construindo um modelo de análise da prática lectiva numa aula de Matemática
Carlos Miguel Ribeiro & Rute Monteiro* e José Carrillo**
*Universidade do Algarve, Portugal
**Universidade de Huelva, Espanha
RESUMO
A prática dos professores pode ser encarada sob distintas perspectivas, sendo uma delas a cognitiva. Apresentamos um modelo que, partindo da prática dos professores, nos permite analisar que cognições se encontram em jogo enquanto estes se encontram imersos na sua prática e também de que forma essas cognições se relacionam e qual o seu papel no processo de ensino. A elaboração de um tal modelo permite-nos simplificar algo tão complexo como o processo de ensino. Neste artigo apresentamos o processo de construção desse modelo, numa aula do 4.º ano do primeiro ciclo em que a professora efectua uma revisão dialogada das diferenças entre quadrados e rectângulos relativamente à medida e nome dos lados. Do modelo ressaltam as cognições evidenciadas pela professora, bem como as relações entre estas e as acções que executa. Terminamos discutindo possíveis implicações do uso deste modelo na formação inicial e contínua de professores.
Palavras-chave: Modelo de ensino; Cognições; Prática lectiva; Matemática
Building a model to analyse a mathematics teacher practice
ABSTRACT
Teaching practice can be seen in different perspectives; one of them is the cognitive perspective. We present a model that, starting from teaching practice, allows us to examine which cognitions are at stake when teachers are immersed in their practice, and also the ways in which those cognitions are related and what is their role in the teaching process. The establishment of such a model allows us to simplify something so complex as the teaching process. In this paper we present the process of construction of such a model, in an elementary 4th grade class in which the teacher makes a dialogued review of the differences between squares and rectangles regarding measurements and number of sides. The model emphasizes the cognition evidenced by the teacher as well as the relations between them and the actions he takes. We finish by presenting the possible implications of the use of this model in the initial and continuing training of teachers.
Keywords: Teaching model; Cognitions; Practice; Mathematics
La construcción de un modelo de Analysis de la práctica lectiva en una classe de matemáticas
RESUMEN
La práctica de los profesores puede ser mirada desde perspectivas distintas, una de ellas la cognitiva. Presentamos un modelo que, partiendo de la práctica de los profesores, nos permite analisar qué cogniciones están en juego cuando estos se encuentran inmersos en su práctica y también de qué forma esas mismas cogniciones se relacionan y cuál es su rol en el proceso de enseñanza. La elaboración de un tal modelo nos permite simplificar algo tan complejo como lo es el proceso de enseñanza. En este artículo presentamos el proceso de construcción de dicho modelo, en una clase de 4º año de primaria en la cual la profesora hace una revisión dialogada de las diferencias entre cuadrados y rectángulos relativamente a la medida y nombre de sus lados. Del modelo surgen las cogniciones evidenciadas por la profesora bien como las relaciones entre estas y las acciones que implementa. Terminamos presentando posibles implicaciones del uso de este modelo en la formación inicial y permanente de los profesores.
Palabras clave: Modelo de enseñanza; Cogniciones; Practicas; Matemáticas
A sala de aula pode ser encarada sob diversas perspectivas e recorrendo a distintos focos de interesse (Esteban, 2006), sendo um deles o professor e a sua prática. O tipo de decisões que o professor toma e a forma como o faz são fundamentais no processo de ensino, pois influenciam todo o seu decurso.
Com o intuito de obtermos um maior entendimento sobre o que se passa na sala de aula, e uma vez que o processo de ensino é por demais complexo, envolvendo inúmeras variáveis (algumas das quais impossíveis, sequer, de equacionar), podemos recorrer a modelos. Assim, e com vista a uma aproximação à prática lectiva do professor, decidimos centrar-nos na sua actuação, considerando como ponto fulcral dessa actuação as possíveis relações existentes entre as suas cognições. Elaboramos, para o efeito, um modelo cognitivo que permite uma simplificação do processo de ensino – pois, como modelo que é, centra-se apenas em algumas das variáveis envolvidas –, possibilitando uma análise mais profícua do mesmo. Para a sua elaboração baseamo-nos nos modelos apresentados por Monteiro (2006), Monteiro, Carrillo e Aguaded (2008), Schoenfeld (1998a, 2000) e Schoenfeld, Ministrell e Zee (2000).
Este artigo enquadra-se numa investigação mais ampla, no âmbito do desenvolvimento profissional, orientada para o estudo das relações entre as cognições de duas professoras do 1.º Ciclo enquanto se encontram imersas na sua prática lectiva e as acções que levam a cabo. Aqui focaremos apenas o caso de uma delas, a professora Maria. Começamos por apresentar o modelo e os seus elementos constituintes, passamos pela contextualização e metodologia utilizada, expondo, de seguida, uma situação exemplificativa da aplicação do modelo num caso concreto. Centramo-nos depois nas relações entre as cognições evidenciadas pela professora, concluindo com algumas reflexões sobre a situação apresentada e as potencialidades da aplicação do modelo no âmbito da formação inicial e/ou contínua de professores.
As distintas componentes do modelo
Por ser um modelo cognitivo, baseia-se fundamentalmente nas cognições – objectivos, crenças e conhecimentos – do professor e, no nosso caso, naquelas que são evidenciadas em pleno decurso da sua prática lectiva, pois consideram-se mais profícuas as investigações baseadas na prática e a partir da prática. Por entendermos que a forma como o professor comunica com os outros (alunos) fornece inúmeras informações sobre si próprio e a visão que tem de si e de todo o processo de ensino, optámos por incluir no modelo, para além das cognições, o tipo de comunicação que ocorre na aula.
Concebendo os objectivos como algo que se pretende atingir (Schoenfeld, 1998b), estes podem ser explícitos ou não, e podem ser tomados numa perspectiva imediata ou longínqua. O professor (ou qualquer indivíduo) poderá inclusivamente não estar completamente consciente do alcance das suas acções e do peso/importância das suas palavras/actuações. Podemos então, à semelhança de Saxe (1991), encarar os objectivos como um fenómeno emergente, possuindo cada indivíduo a capacidade de os construir, adaptar, modelar e remodelar de acordo com o seu próprio percurso, as suas próprias experiências, vivências e conhecimentos, no âmbito da situação específica em que se encontra.
Consideramos que as cognições não existem de forma isolada, coexistindo, relacionando-se e influenciando-se mutuamente, e sendo cada uma delas encarada como parte integrante de um sistema que as contém. Não podemos, portanto, falar de objectivos de forma isolada, mas sim de um sistema cujas diversas componentes (de nível imediato, a médio e longo prazo) se conjugam, de forma preferencialmente simbiótica, para que seja possível uma maior profundidade de alcance no núcleo de tal sistema, de modo a que o conjunto de acções executado com esse fim seja efectivamente proveitoso. Os objectivos (e todas as cognições) podem ser inferidos ou observados; porém, os que mais rica e fidedigna informação nos podem fornecer sobre o processo de ensino são os que se inferem durante o próprio processo, ou seja, os objectivos em acção, sendo, portanto, sobre esses que nos iremos debruçar.
Os objectivos do professor estão em relação directa com as crenças que possui relativamente a todo o processo de ensino. Existem diversas perspectivas segundo as quais podemos analisar crenças, ou como o encaramos sistema de crenças. Uma vez que o processo de ensino é um fenómeno complexo, e não sendo, de todo, nosso objectivo concluir da existência do que se poderá chamar de inconsistências, mas sim compreender os motivos dessa falta de correspondência, coincidimos com Leatham (2006) na consideração das crenças como sistemas sensatos, cuja inconsistência aparente pode dever-se à falta de compreensão, por parte do investigador, da complexidade do fenómeno analisado. O sistema de crenças desempenha, no estudo do processo de ensino, um dos papéis fundamentais, pois uma sua maior compreensão implica, tal como referem Aguirre e Speer (2000), um ampliado conhecimento da sua influência nesse processo. Para efectuar o estudo das crenças, consideraremos os indicadores tomados de um instrumento de análise de crenças de Climent (2005), onde a investigadora, seguindo Carrillo (1998), foca um vasto conjunto de aspectos do conhecimento profissional dos professores do 1.º Ciclo. Note-se que não se pretende associar os professores a determinada tendência didáctica, pois o nosso modelo não é avaliativo (Schoenfeld, 2000), pretendendo-se, sim, obter um maior entendimento acerca do seu processo de ensino.
O conhecimento profissional necessário a cada profissão é sempre algo muito específico dessa profissão. Consideramos que o conhecimento profissional dos professores consiste numa conjunção de todos os saberes e experiências que possuem, e de que fazem uso no desenvolvimento do seu trabalho docente (Estepa, 2000) sendo, portanto, um processo de apropriação dos saberes e vivências pessoais, bem como, necessariamente, da sua interpretação destes. Assim, o conhecimento vai-se construindo desde o início da sua formação e continua durante toda a sua carreira. Além disso, e também por estarem envolvidos na formação das gerações vindouras, contactarem directamente com os alunos e, não raras vezes, com os seus ascendentes, é-lhes fundamental um pleno domínio dos conhecimentos que pretendem ensinar, em todas as suas vertentes.
O conhecimento profissional dos professores pode ser encarado sob diversas perspectivas (e. g. Azcárate, 1999; Ball, Thames e Phelps, 2008; Elbaz, 1981, 1983; Ernest, 1989; Ponte, 1999; Schön, 1983, 1987; Shulman,1986). Porém, neste texto, e por pretendermos também obter uma maior informação relativa ao conhecimento dos professores enquanto estes se encontram imersos na sua própria prática – e não com base nos documentos oficiais –, focar-nos-emos no refinamento elaborado por Ball et al. (2008) das componentes do conhecimento profissional de Shulman (1986). Ball e colegas apresentam uma proposta, ainda em construção, e considerá-la-emos com algumas adaptações, nomeadamente a incorporação de alguns descritores de Park e Oliver (2008).
Ball e colegas (e.g. Ball & Bass, 2003; Ball et al., 2008; Hill, Rowan & Ball, 2005) introduzem a noção de Mathematical Knowledge for Teaching. Dividem o conhecimento do conteúdo e o conhecimento (pedagógico) didáctico geral em três categorias cada. O conhecimento do conteúdo é formado, segundo propõem, pelo Horizon Content Knowledge (HCK), Common Content Knowledge (CCK) – conhecimento comum a qualquer pessoa escolarizada em matemática – e Specialized Content Knowledge (SCK), enquanto que as três componentes do conhecimento didáctico do conteúdo (que contém o conhecimento curricular de Shulman) dizem respeito ao conhecimento do conteúdo e: do ensino (KCT), dos alunos (KCS) e do currículo (KCC).
Muitas acções que os professores realizam nas aulas requerem, da sua parte, um conhecimento matemático específico para o ensino se assim não fosse, qualquer pessoa poderia ensinar, mas o processo de ensino é bem mais amplo do que apenas explicar como se faz e corrigir os erros que possam ocorrer. Considera-se, assim, que aos professores compete possuírem um conhecimento profissional muito próprio/específico, pois, para além de um conhecimento de como fazer isto é, o conhecimento matemático comum (CCK) devem possuir também um conhecimento de como ensinar a fazer. Também Groth (2007) defende a existência de um conhecimento matemático comum que não é suficiente para ensinar, referindo-se explicitamente ao saber calcular com precisão, efectuar exposições matemáticas com correcção e resolver problemas.
Não basta, portanto, um conhecimento do conteúdo que se pretende ensinar, sendo necessário também um conhecimento especializado e específico da profissão docente conhecimento esse que está relacionado com a necessidade de tornar o conteúdo perceptível aos alunos. Assim, por exemplo, mais do que saber apenas determinar o resultado do produto de dois números decimais (considerado CCK), é preciso que o professor possua um conhecimento que facilmente lhe permita perceber e identificar não apenas o erro (o que qualquer indivíduo apto a efectuar o algoritmo faz, mas, essencialmente, a sua fonte (Ball et al., 2008) o que, se lhe for alheia, se torna muito mais complexo (SCK). O professor deverá ser ainda conhecedor de processos alternativos de apresentação/resolução dos conteúdos, para que, sem dificuldade, possa colmatar as lacunas dos seus alunos. Competir-lhe-á, ainda, possuir um conhecimento das relações existentes entre os distintos tópicos matemáticos e de que forma as aprendizagens de um mesmo tópico vão evoluindo ao longo da escolaridade (HCK).
Como parte integrante do conhecimento didáctico e curricular do conteúdo identificado por Shulman (1986) que, recorde-se, foram aglutinados numa só categoria Ball et al. (2008) consideram que os professores devem possuir um conhecimento combinado entre conhecimento sobre o ensino e sobre o conteúdo – matemático (KCT). Este é um tipo de conhecimento que o professor utiliza na aula mesmo em situações que podem não ser vistas especificamente como sendo de exploração de conteúdos, mas que estão relacionadas com os mesmos, em particular: as acções de decidir qual a sequência das tarefas, com que exemplo iniciar, e escolher apropriadamente as representações mais adequadas a cada situação. Park e Oliver (2008) incluem nessa componente do conhecimento profissional também as estratégias específicas de ensino relacionadas com o conteúdo a ser abordado.
No que se refere ao conhecimento do conteúdo e dos alunos (KCS), Ball et al. (2008) relacionam-no com a necessidade de os professores anteciparem o que os alunos pensam, as suas dificuldades (e facilidades) e motivações, bem como de ouvir e interpretar os seus comentários, referindo-se, portanto, a situações em que é exigido que ocorram interacções entre a compreensão matemática e o conhecimento do pensamento matemático dos alunos. Equivalentemente a esta componente, Park e Oliver (2008) consideram o conhecimento das possíveis concepções erróneas, motivações e interesses dos alunos, bem como das suas necessidades.
A forma como o professor comunica com os alunos fornece inúmeras informações sobre si próprio e sobre o modo como se encara a si e a todo o processo de ensino. Fornece indícios sobre a sua postura relativamente a cada assunto, bem como sobre o à-vontade (ou não) com que se relaciona com este, assumindo a comunicação com os alunos um importante papel no que estes aprendem efectivamente (Lampert & Blunk, 1998), e marcando decisivamente a natureza do processo de ensino-aprendizagem da disciplina (Ponte et al., 2007). Essa forma de comunicar encontra-se também relacionada com as suas crenças (Crespo, 2003; Nicol, 1999), pois poderá evidenciar distintas abordagens ao processo de ensino, influenciando, portanto, os indicadores relativos a uma mesma categoria das referidas anteriormente (Climent, 2005). Comunicando de forma distinta, a maneira como leva a cabo cada acção, ou conjunto de acções, será diferente, podendo a perspectiva de ensino ser também substancialmente distinta (o tipo de comunicação é reflectido no modo de ensinar do professor, pelo que, dentro de uma mesma categoria, influencia o tipo de indicador atribuído em cada episódio).
Existem diversas teorias de comunicação, dependendo da área em que nos movemos. Há quem considere a comunicação como transmissão de informação, domínio em que, basicamente, se postula a existência de um emissor e um receptor, circulando a comunicação entre estes, mas não sendo os elementos particulares tidos em conta no processo. Se entendermos que, pelo contrário, existe uma interacção entre os participantes, e que nesta interacção ocorre uma negociação de significados, estamos a conceber a comunicação como um processo de interacção social (Belchior, 2003; Ferin, 2002; Sierpinska, 1998). Iremos focar-nos nesta perspectiva da comunicação como interacção social, mas apenas na óptica do professor, sem abordar/discutir o tipo de interacções que ocorrem entre os alunos e a sua importância no processo de ensino. Centrando-nos especificamente no tipo de comunicação oral do professor, adoptamos a classificação de Brendefur e Frykholm (2000), com algumas adaptações colhidas de Carrillo, Climent, Gorgorió, Rojas e Prat (2008).
Brendefur e Frykholm (2000) propõem quatro tipos de comunicação matemática: unidireccional, contributiva, reflexiva e instrutiva. A comunicação unidireccional encontra-se associada a um ensino mais tradicional, em que o professor assume o papel principal, e ao aluno compete apenas reproduzir textualmente o que ouve. Quando o professor recorre a uma comunicação contributiva, ao aluno é já facultada alguma participação no decurso da aula; porém, as interacções que ocorrem são fundamentalmente de natureza correctiva, não se aprofundando o conteúdo. Na comunicação reflexiva, as interacções ocorridas na sala de aula, entre alunos e professor, são detonantes das investigações a ocorrer. Tal como Carrillo et al. (2008), consideramos que a modificação da compreensão matemática dos alunos é própria das actividades de investigação que lhes são facultadas. Ao comunicar de forma instrutiva, o professor, para além do que se verifica ao recorrer a uma comunicação reflexiva, pretende fornecer algumas "luzes" sobre o conteúdo que se irá abordar de seguida, promovendo uma integração das ideias dos alunos na prática – avanços e/ou dificuldades –, sejam essas ideias manifestadas ou intuídas, pelo professor ou pelos próprios alunos.
Elementos constituintes do modelo
Este modelo cognitivo – que apresentamos na Figura 1 baseado nos de Monteiro (2006), Monteiro et al. (2008), Schoenfeld (1998a, 2000) e Schoenfeld et al. (2000), parte da prática, sendo construído a partir dela. O modelo baseia-se na divisão de cada aula, tomada como um todo, em partes fenomenologicamente coerentes (Schoenfeld, 1998a, 1998b), denominadas episódios, correspondendo cada um deles a um determinado objectivo específico. Estes episódios são delimitados por eventos de início (desencadeante) e de término, os quais encerram em si o objectivo específico, que dá o nome ao episódio. Os episódios são delimitados pelas linhas da transcrição correspondente, e cada evento de término precede imediatamente um outro evento desencadeante de outro episódio.
Apresentação gráfica do modelo cognitivo e seus elementos constituintes

Entre cada um destes eventos decorre o episódio, e nele identificamos não só as cognições, mas também o seu tipo, distinguindo-se o facto de pertencer, ou não, à imagem da lição. A imagem da lição é entendida como uma antevisão, do professor, do que irá ocorrer e como irá decorrer a aula, imediatamente antes do seu início. Esta antevisão é verbalizada instantes antes do início da própria aula e não deve, portanto, ser confundida com a planificação da mesma. Para cada episódio são identificados: os indicadores de crenças (Climent, 2005); o conteúdo; o objectivo específico; os conhecimentos do professor necessários para o implementar (Ball et al., 2008; Park & Oliver, 2008); o tipo de episódio; o tipo de comunicação; a forma de trabalho; e os recursos utilizados. É ainda analisado se o episódio faz parte, ou não, da imagem da lição (veja-se a figura).
O tipo de episódio diz respeito às sequências de acção executadas pelo professor, que podem corresponder a rotinas, scripts ou guiões de acção, e a improvisações (Monteiro, 2006; Monteiro et al., 2008; Schank & Abelson, 1977; Schoenfeld, 2000; Schoenfeld et al., 2000; Sherin et al., 2000). Entende-se por rotina toda a acção independente do conteúdo, executada de forma rotineira. Os scripts, ou guiões de acção, são especializações de rotinas, mas com dependência conceptual. As improvisações correspondem a todas as acções que o professor leva a cabo como resposta a algum evento que ocorre de forma inesperada. Consideramo-las (Ribeiro et al., 2009) num sentido mais amplo do que o dos autores anteriormente referidos, pois diferenciamo-las, de acordo com a relação que os acontecimentos/acções têm, ou não, com os conteúdos, por improvisações de conteúdo e improvisações de gestão. Às improvisações de conteúdo estão associados, necessariamente, objectivos emergentes, sendo, portanto, as situações em que, de modo bastante vincado, são evidenciadas as cognições do professor, já que, nestes casos, é necessária uma reacção/resposta intuitiva. As de gestão não têm relação com os conteúdos abordados e ocorrem, por exemplo, quando alguém do exterior interrompe o decurso da aula.
Achamos também importante incluir no modelo o tipo de comunicação, a forma de trabalho e os recursos utilizados, pois o modo como têm intervenção directa no processo de ensino poderá fornecer-nos informações mais profícuas quanto às relações que se verificam efectivamente entre as cognições em acção.
Para a inclusão no modelo, como vimos anteriormente, centramo-nos especificamente nos quatro tipos de comunicação oral do professor propostos por Brendefur e Frykholm (2000), com algumas adaptações de Carrillo et al. (2008). Esta comunicação é levada a cabo utilizando diversas estratégias comunicativas/tipos de diálogos, como sejam, por exemplo: o diálogo interactivo, o socrático, o não planeado, o monólogo e a mini apresentação (Schoenfeld, 1998a, 1998b, 2000; Schoenfeld et al., 2000). É de salientar o facto de considerarmos que, numa aula, a comunicação não é necessariamente toda do mesmo tipo, podendo variar durante o seu decurso. A identificação, em cada situação/episódio, deverá, portanto, ser efectuada pelo modo predominante de comunicação matemática que ocorre. Esta predominância não deverá ser contabilizada numericamente, mas sim pela importância que os episódios/acontecimentos representam para o decurso da mesma.
Quanto à forma de trabalho, refere-se, tal como o nome indica, ao modo de trabalhar dos alunos e a como o desenvolvem, nomeadamente que recursos utilizam em cada episódio para levar a cabo o objectivo que se lhe encontra associado.
De maneira a evidenciar como concebemos graficamente o modelo que iremos utilizar, apresentamos, na Figura 1, o seu aspecto gráfico, bem como a localização das componentes no mesmo, considerando que corresponde ao j-ésimo episódio da i-ésima aula transcrita pertencente à segunda fase (aula resultante do período de trabalho colaborativo), que denominamos por [II.i.j], que tem n acções, representadas, do lado direito por [II.i.j.n].
Contextualização e metodologia
Neste texto apresentamos e discutimos o processo de elaboração de um modelo cognitivo do processo de ensino, a partir do qual se torna possível uma análise mais sistemática às cognições do professor enquanto se encontra imerso na sua prática lectiva. Em particular, apresentamos e discutimos a modelação de um episódio de revisão dialogada do conteúdo (diferenças entre quadrados e rectângulos relativamente à medida e nomes dos lados) numa turma do 4.º ano de escolaridade de uma vila do barlavento Algarvio, leccionada por uma professora – Maria – com 18 anos de prática e que pertencia a um grupo de trabalho colaborativo formado por duas professoras do 1.º Ciclo e o investigador, encontrando-se ambas também, em simultâneo, a frequentar o Programa de Formação Contínua em Matemática para professores do 1.º e 2.º Ciclos (PFCM) 2. Este estudo faz parte de uma investigação mais ampla, no âmbito do desenvolvimento profissional, orientada para o estudo das relações entre crenças, conhecimentos, objectivos e acções do professor. Nela combina-se o estudo de caso (Ponte, 1994; Stake, 1998, 2000; Yin, 1993) com uma metodologia de cariz interpretativo onde o investigador é não interveniente.
Com o intuito de apresentar o modelo e evidenciar as cognições e suas relações, discutiremos alguns dos fundamentos teóricos subjacentes ao mesmo, ilustrando o processo de modelação do ensino com recurso a um excerto de uma aula – associado ao objectivo específico de recapitular as diferenças entre quadrados e rectângulos relativamente à medida e nomes dos lados – e evidenciando o tipo de relações que se estabelecem entre as diversas acções da professora, para levar a bom porto o objectivo específico e as crenças associadas.
Por se centrar na professora enquanto esta se encontrava no exercício da sua prática lectiva, a recolha de dados – gravação de aulas em áudio e vídeo – ocorreu no seu local de trabalho, tendo-a como foco, e decorreu em três fases distintas ao longo do ano, correspondendo, portanto, a três conteúdos diferentes (mas sempre durante o período de introdução dos mesmos), e que se desenvolveram com envolvências distintas por parte dos participantes. A primeira fase correspondeu a uma recolha de dados onde se pretendia obter um ponto de partida (estado da arte), a segunda ao resultado de um trabalho colaborativo (complementar ao que decorria normalmente no âmbito do PFCM) envolvendo os três participantes – as duas professoras do 1.º Ciclo e o investigador –, e a terceira fase associou-se a um trabalho pós colaborativo, não tendo tido o investigador qualquer intervenção na discussão da preparação das aulas.
De modo a obter algumas informações que se consideravam pertinentes para a inclusão no modelo – imagem da lição –, foram realizadas conversas informais antes (para se ter uma antevisão da aula) e depois de cada aula (para clarificar algumas inferências). A gravação em vídeo permitiu registar as interacções ocorridas entre professora e alunos, bem como facilitar, de modo substancial, a realização da análise da aula, por via da sua posterior visualização.
Após as gravações, foi efectuada a transcrição áudio, complementada com vídeo (Figura 2). Esta transcrição, linha-a-linha, é, efectivamente, o primeiro passo da elaboração do modelo (Schoenfeld et al., 2000), pois reflecte as efectivas interacções que ocorrem entre os agentes educativos – alunos e professor –, bem como a forma como ocorrem, correspondendo cada mudança propositada de linha a uma mudança de interacção/intervenientes. O período de transcrição corresponde a uma primeira fase na modelação, dado que foi efectuada, logo ali, a decomposição de cada aula em episódios, identificando-se o objectivo específico em cada momento, bem como os eventos de início e de término que lhes estão associados.
Figura 2
Transcrição de um excerto da segunda aula, da segunda fase, relativamente à revisão de diferenças entre quadrados e rectângulos e à medida e nomes dos lados

Depois de divididas todas as aulas correspondentes a um mesmo período de trabalho, foram agrupados todos os episódios do mesmo tipo (com o mesmo tipo de objectivo) e foi efectuada a intersecção dos indicadores de crenças (Climent, 2005), que resultam como sendo os indicadores associados àquele tipo de episódio. Para os conhecimentos, o processo foi similar; porém, foi efectuada a reunião de todos os conhecimentos identificados, obtendo-se assim o conhecimento profissional da professora, envolvido naquela fase específica, relacionado com cada tipo próprio de episódio.
O processo de modelação
Para a ilustrar o processo de construção do modelo, apresenta-se um excerto de uma transcrição da segunda aula, da segunda fase, fase esta, em que a professora, durante três aulas, aborda as medidas de área padrão e as relações entre estas. Este é um episódio associado a um objectivo que a professora não tinha inicialmente equacionado (rever as diferenças entre quadrados e rectângulos relativamente à medida e nomes dos lados) e que surgiu do decurso da aula, correspondendo, portanto, a uma improvisação de conteúdo.
Uma vez que um episódio não poderá ser entendido de forma isolada e descontextualizada, sob pena de a análise efectuada não ter qualquer sentido no âmbito da investigação da qual faz parte, considera-se importante uma pequena contextualização, que passamos a apresentar.
No episódio imediatamente anterior, correspondente a um episódio de construção do conteúdo 3, são exploradas, de forma instrutiva, em grupos (quartetos), colaborativamente, e tendo como recurso material manipulável (1dm 2 ), formas de determinar a área de um rectângulo (mesa da sala) – quer seja utilizando superfícies distintas (quadrados, triângulos, rectângulos), quer seja através do recurso à fórmula da área. Nesse contexto, e sem que o tivesse programado/pensado – daí corresponder a uma improvisação, e de conteúdo, pois está directamente relacionada com conteúdos específicos –, aproveitando um comentário de um aluno, a professora sente necessidade de efectuar uma revisão das diferenças entre quadrados e rectângulos, em particular no que concerne aos nomes dos lados, e fá-lo dialogando de forma contributiva para o grande grupo (grupo turma). Este é um tipo de revisão que ocorria já com frequência durante a primeira fase de recolha de dados. Posteriormente a este episódio, a professora retoma o seu plano e apresenta aos alunos a definição de dm 2 como sendo um quadrado com um decímetro de lado. Esta apresentação é efectuada de forma reflexiva, em grande grupo, colaborativamente, e com recurso a material manipulável.
Na transcrição que a seguir se apresenta, P refere-se à professora, A a um aluno e As a vários alunos. Nas linhas da transcrição em que se omite o agente enunciador, considera-se que se mantém o mesmo que anteriormente.
Para a obtenção desta parte da transcrição, correspondente a um episódio, foram já efectuados alguns dos passos do processo de modelação, tais como a identificação dos eventos de início (P pega num dos quadrados com um decímetro de lado) e de término (P reforça a resposta dos alunos face ao número de quadrados com 1dm de lado necessários para cobrir a mesa) e a identificação do objectivo da professora neste momento específico (recapitular a diferença entre quadrados e rectângulos relativamente à medida e nomes dos lados) que, tal como foi já referido, está em relação directa com a nomenclatura do próprio episódio.
Entre os eventos de início e de término do episódio, a professora leva a cabo algumas acções, as quais se encontram associadas a crenças e conhecimentos. Neste episódio específico, a professora executa duas acções distintas – recapitular e clarificar o conteúdo – que são dependentes do tipo de comunicação que utiliza, influenciando assim, directamente, tanto os indicadores de crenças como as componentes do conhecimento profissional identificados.
As duas acções que a professora executa neste tipo de episódios de revisão – revisão dialogada – são, também por esta ser a forma mais simples de rever o conteúdo, as bases de todos os episódios de revisão e, pelas evidências, encontram-se associadas a indicadores de crenças (Climent, 2005) que se transformam assim, também eles, nas bases do sistema de crenças aquando de uma revisão do conteúdo, independentemente dos recursos ou agrupamentos que utiliza, podendo diferir apenas no que respeita ao tipo de comunicação que é utilizado. Quanto aos conhecimentos, e uma vez que estão mais directamente relacionados com os conteúdos abordados, em cada episódio a professora evidencia uns muito específicos daí que a identificação dos conhecimentos correspondentes a cada tipo de episódio seja efectuada pela reunião de todos os identificados em cada ocorrência de um mesmo tipo de episódio.
Dado que um modelo se quer simplificativo da situação analisada, com vista a tornar o seu manuseamento mais acessível, e a tornar a análise das relações exequível e mais profícua, seguindo o que foi referido anteriormente, apresentamos as cognições reveladas no episódio descrito, recorrendo a um desenho dinâmico que nos permite uma fácil visualização das suas componentes. A cada uma destas acções da professora encontram-se associados os indicadores de crenças e os conhecimentos evidenciados neste caso específico. Apesar de as acções serem aqui apresentadas pela ordem cronológica pela qual ocorrem, por uma questão de simplificação, não significa isso que, noutras ocorrências deste tipo de episódio, tenham de suceder necessariamente por essa ordem (dependendo do decurso da aula), demonstrando-se assim também a complexidade da mente humana e do próprio processo de ensino.
Figura 3
Modelação de um episódio da segunda aula, da segunda fase [II.2.15], da professora Maria relativamente à revisão de diferenças entre quadrados e rectângulos e à medida e nomes dos lados

Da identificação dos conhecimentos profissionais ressalta que, neste episódio, não se registe o recurso ao SCK, embora a professora deixe perceber uma sua carência que se manifesta em KCS, pois poderá induzir os alunos em erro, levando-os a confundir caracterização de quadrados com enumeração de propriedades.
Podemos apresentar as relações entre acções e cognições recorrendo a um esquema que, apesar de não introduzir novas informações, permite observar mais claramente o tipo de relações que se verifica entre as diversas acções da professora para concretizar este objectivo específico, bem como as crenças e conhecimentos associados.
Figura 4
Relações entre acções, crenças e objectivo da professora Maria aquando da revisão dialogada do conteúdo (diferenças entre quadrados e rectângulos e à medida e nomes dos lados), de forma contributiva e em grupo
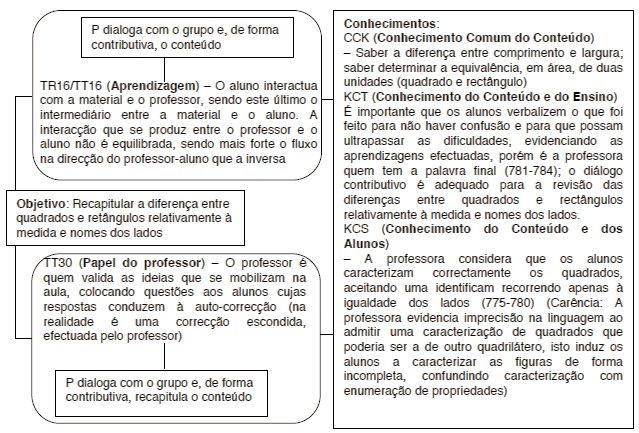
Com esta apresentação esquemática das relações, pretende-se também evidenciar, de forma clara, o facto de ocorrerem activações prioritárias de acções e/ou de crenças associadas mutuamente, ou seja, o não se considerar que se verifica uma supremacia de umas em detrimento de outras. De modo a conseguir alcançar o objectivo emergente a que se tinha proposto, a professora recorre a componentes do conhecimento profissional que se encontram associadas, fundamentalmente, ao conhecimento que possui do processo de ensino (KCT) e dos seus alunos (KCS), pois não se verificam evidências de que, nesta situação, recorra a um conhecimento específico para o ensino (SCK) e, mesmo no conhecimento comum, revela uma carência, que se manifesta posteriormente no KCS, relativamente ao facto de julgar suficiente para caracterizar os quadrados referir a igualdade da medida dos lados.
Estas acções e o tipo de comunicação a que se encontram associadas permitem à professora exteriorizar as suas cognições predominantes nesta situação específica que, por ser uma improvisação de conteúdo, corresponde, quanto a nós (Ribeiro et al., 2009), a um dos tipos de situações/episódios em que, mais marcadamente, entram em jogo todas as suas cognições na forma mais pura, pois reflectem efectivamente o seu modo de actuação e postura face a todo o processo e intervenientes.
O modelo na formação inicial e/ou contínua de professores
A elaboração deste tipo de modelo poderia ser implementada tanto na formação inicial como na contínua, de modo a que, associada a um processo reflexivo, os professores (ou futuros professores) pudessem consciencializar-se das suas próprias cognições. O processo de modelação, e as consequentes discussões e reflexões, poderia representar, inclusivamente, um possível ponto de partida para as discussões das suas aulas, focando-se em aspectos verdadeiramente pertinentes e deixando de lado aspectos acessórios (Star & Strickland, 2008), tal como sejam somente dados relacionados com o conhecimento, ou não, dos processos de ensino – uma parte de KCT –, abdicando da componente que se refere ao conteúdo concreto que se aborda (no caso dos professores ou futuros professores dos primeiros anos, independente da área curricular a que se refere).
Através do processo de elaboração do seu próprio modelo de ensino, seria possível aos professores não só consciencializarem-se das suas cognições, o que permitiria a sua discussão e a reflexão sobre o seu papel no processo de ensino, mas também identificarem e consciencializarem-se de algumas possíveis lacunas ou efectivas necessidades de adequação/formação no seu conhecimento profissional. No que concerne aos futuros professores e, por acréscimo, também aos seus supervisores/professores acompanhantes, este processo, e consequente tomada de consciência acerca da forma como se relacionam as cognições e como influenciam o processo de ensino, permitir-lhes-ia assumir uma postura mais crítica (e não apenas submissa) quando realizam as suas práticas.
Nos programas de formação contínua, este poderia ser o ponto de partida a considerar, sendo o aspecto fulcral da identificação das efectivas necessidades de formação dos professores, partindo da sua própria prática. Esta é, aliás, uma das premissas seguidas para a elaboração do próprio modelo que se baseie na prática, pois apenas a partir dela poderão ocorrer efectivas alterações/adequações face às Orientações Ministeriais dado que, tal como referem também Tichá e Hopesová (2006), para que se verifique uma alteração das crenças (cognições) dos professores sobre o sentido e significado que atribuem ao ensino da Matemática, o modo como se encontram preparados para este e do seu conceito de actividade matemática, não é suficiente o facto de lhes ser fornecida informação acerca de outros tipos possíveis de abordagem na aprendizagem da Matemática. É, portanto, necessário, e mesmo fundamental, que se considere a sua própria sala de aula como ponto de partida.
A professora Maria seguiu o processo de visualização (Rochelle, 2000; Santagata et al,, 2007; Sherin, 2004) e reflexão sobre as suas próprias aulas e acompanhamento da elaboração do seu modelo de ensino, o que lhe permitiu também uma reflexão sobre a sua própria prática (Schön, 1983, 1987) e uma consciencialização acerca das suas cognições e postura face a todo o processo de ensino. Apesar de não ter sido ela própria a elaborar o seu modelo, efectuou um acompanhamento muito próximo, seguindo todos os passos do mesmo. Todo este processo e sua importância foram explanados no portefólio que realizou no âmbito do PFCM. Esta reflexão individual, acompanhada de discussão e reflexão crítica com outros colegas e investigadores, considera-se um primeiro passo para um sustentado desenvolvimento profissional (Climent & Carrillo, 2003; Jaworski, 2006).
REFERÊNCIAS
Aguirre, J., & Speer, N. (2000). Examining the relationship between beliefs and goals in teacher practice. Journal of Mathematical Behaviour, 18(3), 327-356. [ Links ]
Azcárate, P. (1999). El conocimiento profesional: Naturaleza, fuentes, organización y desarrollo. Quadrante, 8, 111-138. [ Links ]
Ball, D. L., & Bass, H. (2003). Toward a practice-based theory of mathematical knowledge for teaching. In B. Davis & E. Simmt (Eds.), Proceedings of the 2002 Annual Meeting of the Canadian Mathematics Education Study Group (pp. 3-14). Edmonton, AB: CMESG/GCEDM. [ Links ]
Ball, D. L., Thames, M. H., & Phelps, G. (2008). Content knowledge for teaching: What makes it special? Journal of Teacher Education , 59(5), 389-407. [ Links ]
Belchior, F. H. (2003). Pedagogia, comunicação e existência. Revista Portuguesa de Pedagogia, 37(3), 197-230. [ Links ]
Brendefur, J., & Frykholm, J. (2000). Promoting mathematical communication in the classroom: Two preservice teachers' conceptions and practices. Journal of Mathematics Teacher Education, 3, 125-153. [ Links ]
Carrillo, J. (1998). Modos de resolver problemas y concepciones sobre la Matemática y su enseñanza: Metodología de la investigación y relaciones. Huelva: Universidad de Huelva Publicaciones. [ Links ]
Carrillo, J., Climent, N., Gorgorió, N., Rojas, F., & Prat, M. (2008). Análisis de secuencias de aprendizaje matemático desde la perspectiva de la gestión de la participación. Enseñanza de las Ciencias, 26(1), 67-76. [ Links ]
Climent, N. (2005). El desarrollo profesional del maestro de Primaria respecto de la enseñanza de la Matemática. Un estudio de caso . Tesis Doctoral. Michigan: Proquest Michigan University. [ Links ]
Climent, N., & Carrillo, J. (2003). El dominio compartido de la investigación y el desarrollo profesional. Una experiencia en matematicas con maestras. Enseñanza de las Ciencias, 21(3), 387-404. [ Links ]
Crespo, S. (2003). Learning to pose mathematical problems: Exploring changes in preservice teachers' practices. Educational Studies in Mathematics, 52(3), 243-270. [ Links ]
Elbaz, F. (1981). The teachers' "practical knowledge": Report of a case study. Curriculum Inquiry, 11, 43-71. [ Links ]
Elbaz, F. (1983). Teacher thinking: A study of practical knowledge. Londres: Croom Helm. [ Links ]
Ernest, P. (1989). The knowledge, beliefs and attitudes of Mathematics teacher: A model. Journal of Education for Teaching , 15(1), 13-33. [ Links ]
Esteban, M. T. (2006). Sala de aula – Dos lugares fixos aos entre lugares fluidos. Revista Portuguesa de Educação, 19(2), 7-20. [ Links ]
Estepa, J. (2000). El conocimiento profesional de los profesores de Ciencias Sociales. In J. Pagés, J. Estepa & G. Travé (Eds.), Modelos, contenidos y experiencias en la formación profesional del profesorado de Ciencias Sociales. Huelva: Universidad de Huelva Publicaciones. [ Links ]
Ferin, I. (2002). Comunicação e culturas do quotidiano. Lisboa: Quimera. [ Links ]
Groth, R. E. (2007). Toward a conceptualization of statistical knowledge for teaching. Journal for Research in Mathematics Education, 38(5), 427-437. [ Links ]
Hill, H. C., Rowan, B., & Ball, D. L. (2005). Effects of teachers' mathematics knowledge for teaching on student achievement. American Education Research Journal, 42(2), 371-406. [ Links ]
Jaworski, B. (2006). Theory and practice in Mathematics teaching development: Critical inquiry as a mode of learning in teaching. Journal of Mathematics Teacher Education, 9(2), 187-211. [ Links ]
Lampert, M., & Blunk, M. L. (1998). Talking Mathematics in school: Studies of teaching and learning. Cambridge, UK: Cambridge University Press. [ Links ]
Leatham, K. R. (2006). Viewing Mathematics teachers' beliefs as sensible systems. Journal of Mathematics Teacher Education , 9, 91-102. [ Links ]
Monteiro, R. (2006). La enseñanza de las Ciencias Naturales desde el análisis cognitivo de la acción. Unpublished Tesis Doctoral. Huelva: Universidad de Huelva. [ Links ]
Monteiro, R., Carrillo, J., & Aguaded, S. (2008). Emergent theorizations in modeling the teaching of two Science teachers. Research in Science Education, 38(3), 301-319. [ Links ]
Nicol, C. (1999). Learning to teach Mathematics: Questioning, listening, and responding. Educational Studies in Mathematics, 37, 45-66. [ Links ]
Park, S., & Oliver, J. S. (2008). Revisiting the conceptualization of pedagogical content knowledge (PCK): PCK as a conceptual tool to understand teachers as professionals. Research in Sciences Education , 38, 261-284. [ Links ]
Ponte, J. P. (1994). O estudo de caso na investigação em Educação Matemática. Quadrante, 3(1), 3-18. [ Links ]
Ponte, J. P. (1999). Didácticas específicas e construção do conhecimento profissional. In J. Tavares, A. Pereira, A. P. Pedro & H. A. Sá (Eds.), Investigar e Formar em Educação: Actas do IV Congresso da SPCE (pp. 59-72). Porto: SPCE [ Links ]
Ponte, J. P., Guerreiro, A., Cunha, H., Duarte, J., Martinho, H., Martins, C., Menezes, L., Menino, H., Pinto, H., Santos, L., Varandas, J. M., Veia, L., & Viseu, F. (2007). A comunicação nas práticas de jovens professores de Matemática. Revista Portuguesa de Educação, 20(2), 39-74. [ Links ]
Ribeiro, C. M., Monteiro, R., & Carrillo, J. (2009). Professional knowledge in an improvisation episode: The importance of a cognitive model. In V. D. Guerrier, S. Soury-Lavergne & F. Arzarello (Eds.), Proceedings of the 6th Conference of the European Society for Research in Mathematics Education (CERME 6) (pp. 2030-2039). Lyon, France: ERME. [ Links ]
Rochelle, J. (2000). Choosing and using video equipment for data collection. In A. Kelly & R. Lech (Eds.), Handbook of research design in Mathematics and Science Education (pp. 709-732). Londres: Lawrence Erlbaum Associates Publishers. [ Links ]
Santagata, R., Zannoni, C., & Stigler, J. W. (2007). The role of lesson analysis in pre-service teacher education: An empirical investigation of teacher learning from a virtual video-based field experience. Journal of Mathematics Teacher Education, 10(2), 123-140. [ Links ]
Saxe, G. (1991). Culture and cognitive development: Studies in mathematical understanding. Hillsdale: Lawrence Erlbaum Associates. [ Links ]
Schank, R. C., & Abelson, R. P. (1977). Scripts, plans, goals, and understanding: An inquiry into the human knowledge structures. Hillsdale: Lawrence Erlbaum Associates. [ Links ]
Schoenfeld, A. H. (1998a). On modeling teaching. Issues in Education, 4(1), 149-162. [ Links ]
Schoenfeld, A. H. (1998b). Toward a theory of teaching-in-context. Issues in Education, 4(1), 1-94. [ Links ]
Schoenfeld, A. H. (2000). Models of the teaching process. Journal of Mathematical Behavior, 18(3), 243-261. [ Links ]
Schoenfeld, A. H., Ministrell, J., & Zee, E. v. (2000). The detailed analysis of an established teacher's non-traditional lesson. Journal of Mathematical Behavior, 18(3), 281-325. [ Links ]
Schön, D. (1983). The reflective practitioner: How professionals think in action. Nova York: Basic Books Inc. Publishers. [ Links ]
Schön, D. (1987). Educating the reflective practitioner: Toward a new design for teaching and learning in the professions. San Francisco, CA: Jossey Bass. [ Links ]
Serrazina, L., Canavarro, A., Guerreiro, A., Rocha, I., Portela, J., & Saramago, M. J. (2005). Programa de formação contínua em Matemática para professores do 1.º Ciclo (documento não publicado). [ Links ]
Sherin, M. G. (2004). New perspectives on the role of video in teacher education. In J. Brophy (Ed.), Using video in teacher education (pp. 1-28). Oxford: Elsevier Ltd. [ Links ]
Sherin, M. G., Sherin, B. L., & Madanes, R. (2000). Exploring diverse accounts of teacher knowledge. Journal of Mathematical Behavior, 18(3), 357-375. [ Links ]
Shulman, L. (1986). Those who understand: Knowledge growth in teaching. Educational Researcher, 15(2), 4-14. [ Links ]
Sierpinska, A. (1998). Three epistemologies, three views of classroom communication: Constructivism, sociocultural approaches, interactionism. In H. Steinbring, M. G. B. Bussi & A. Sierpinska (Eds.), Language and communication in the Mathematics classroom (pp. 30-62). Reston, VA: NCTM. [ Links ]
Stake, R. E. (1998). Investigación con estudio de casos. Madrid: Ediciones Morata. [ Links ]
Stake, R. E. (2000). Qualitative case studies. In N. K. Denzin & Y. Lincoln (Eds.), Handbook of qualitative research (pp. 435-454). Thousand Oaks: Sage. [ Links ]
Star, J. R., & Strickland, S. K. (2008). Learning to observe: Using video to improve preservice Mathematics teachers' ability to notice. Journal of Mathematics Teacher Education, 11(2), 107-125. [ Links ]
Tichá, M., & Hopesová, A. (2006). Qualified pedagogical reflection as a way to improve Mathematics education. Journal of Mathematics Teacher Education, 9, 129-156. [ Links ]
Yin, R. K. (1993). Applications of the case study research. Thousand Oaks, CA: Sage Publications. [ Links ]
Toda a correspondência relativa a este artigo deve ser enviada para:Carlos Miguel Ribeiro, e-mail cmribeiro@ualg.pt
Recebido em Dezembro, 2008
Aceite para publicação em Junho, 2011
Agradecimentos
Este artigo foi parcialmente financiado pela Fundação para a Ciência e a Tecnologia.
Este trabalho forma parte do Projecto "Conocimiento matemático para la enseñanza respecto a la resolución de problemas y el razonamiento" (EDU2009-09789), Dirección General de Investigación y Gestión del Plan Nacional de I+D+i. Ministerio de Ciencia e Innovación (Espanha).
NOTAS
1 Grande parte das acções que se verificam durante o decurso de uma aula iniciam-se com a professora a dialogar com os alunos.
2 Este Programa de Formação teve origem no despacho conjunto n.º 812/2005 (2.ª série), do Diário da República – II série, n.º 204, de 24 de Outubro de 2005, onde foi criada uma comissão de acompanhamento que definiu que o portefólio reflexivo (onde constassem, o guião, descrição e reflexão de duas aulas) seria o seu instrumento de avaliação (Serrazina et al., 2005).
3 Este tipo de episódio refere-se concretamente àqueles em que a professora faculta aos alunos a oportunidade de irem construindo os conceitos/conhecimentos/ relações à medida que desenvolvem as actividades.













