1. Introduction

Any quantitative method is shaped by certain rules or assumptions that constitute its own rationale (^{Gauer et al., 2010}; ^{Golino & Gomes, 2014}a, ²⁰¹⁴b, ²⁰¹⁶; ^{Gomes, 2020}; ^{Gomes & Almeida, 2017}; ^{Gomes et al., 2019}; ^{Gomes & Valentini, 2019}; ^{Pereira et al., 2019}). They provide the conditions as well the constraints which determine how the evidence can be constructed (^{Gomes et al., 2017}; ^{Gomes & Gjikuria, 2017}; ^{Gomes et al., 2013}; ^{Gomes & Jelihovschi, 2016}). For example, factor analysis (^{Gomes, Linhares et al., 2021}; ^{Matos et al., 2019}) and item response theory (^{Golino et al., 2015}; ^{Golino & Gomes, 2019}; ^{Gomes, 2013}) assume that scientific constructs are latent variables that explain the variance of observable variables, which are, in general, respondents’ performance in tasks (^{Gomes & Nascimento, 2021}; ^{Gomes et al., 2021}a, ^2021b, ^2021c) or respondents’ self-reports about certain statements, words, and so on (^{Fleith & Gomes, 2019}; ^{Gomes, Araujo et al., 2020}). When factor analysis or item response theory estimate latent variables in an individual, the time parameter is added, usually assuming that the previous response has an influence over the individual’s response (^{Ferreira & Gomes, 2017}; ^{Gomes et al., 2018}; ^{Rodrigues & Gomes, 2020}). These rules constrain the evidence that can be constructed by the researcher. In other words, factor analysis and item response theory transform information from data into knowledge through a frame that bind latent and observable variables in a linear structure. In sum, the rationale of any quantitative method is both a possibility and a restriction required as the evidence is being constructed (^{Jelihovschi & Gomes, 2019}; ^{Pires & Gomes, 2017}, ²⁰¹⁸).

Educational large-scale assessments, such as the International Association for the Evaluation of Educational Achievement (IEA) (^{Härnqvist, 1975}), the Programme for International Student Assessment (PISA) (^{OECD, 2019}), and the National Exam of Upper Secondary Education (ENEM) (^{Brasil/INEP, 2015}) are, essentially, complex datasets. Some properties that constitute these assessments as complex datasets are the following: (1) They have large amounts of information about students and their socioeconomic, psychological, familiar, and educational backgrounds; (2) not by chance, they involve many non-linear relationships among the variables; (3) besides, they have a large set of nominal variables with many categories. For example, the variable country in PISA has dozens of countries, and the variables states of Brazil in ENEM has dozens of states; (4) they have many ordinal variables, whose distances between their values, at least conceptually, is not the same.

The General Linear Model (i.e. Structural Equation Modeling, Multiple Regression, Multilevel Regression, ANOVA, correlations) is the mainstream approach in Education. However, its use in complex datasets is very questionable. The techniques from the General Linear Model can model nonlinear relationships among variables, and deal with nominal and categorical variables with many variables, but they do it through difficult ways.

The General Linear Model can only estimate non-linear relationships that are previously modeled by the analyst and inserted a priori in the model, so, in this way, many non-linear relations may be lost. For example, if the analyst suspects that there is a non-linear relationship between engagement and achievement, then he/she needs to introduce this non-linear relationship in the model, also defining the kind of non-linearity she believes is occurring between these variables, otherwise it will not work, that is, what is not modeled will not be identified and considered in the analysis. Since the General Linear Model is the mainstream in Education, being extensively applied in educational complex datasets (i.e. large-scale assessments), we may infer that many non-linear relationships between predictors and outcomes have been lost or not identified.

The General Linear Model is not suitable to deal with nominal variables with many categories. As an example, ENEM has a nominal variable with 27 categories, representing the States of Brazil. One common approach of the General Linear Model to deal with this variable is to transform the variable in 26 dummy variables, taking one category from the 27 categories as reference. For example, if the Category A (Minas Gerais State) is taken as the reference, all other categories (States of Brazil) will be compared only with this category (Minas Gerais State). Therefore, the slopes of the other dummy variables, representing the other categories, are estimated in comparison to the category A (Minas Gerais State). This is a real problem, because if the researcher wants to understand how the slope of the category B (Rio de Janeiro State) is related to the slope of the category C (São Paulo State), she will not be able to do that since all the slopes are comparable only to the slope of the category A (Minas Gerais State). This drawback of linear models narrows down substantially the information and interpretation from the data, compromising the constructed evidence from these models.

The General Linear Model is not appropriate for dealing with ordinal variables. It assumes, incorrectly, that ordinal variables are scales, that is, the distances between any two of their values are the same. This incorrect assumption is an issue. Educational large-scale datasets are plentiful of ordinal variables. Let’s see an example. Suppose that an ordinal variable of motivation to study has three discrete values: 1- no motivation, 2- weak motivation, and 3- strong motivation. The General Linear Model assumes that the distance between the value 1 and value 2 is the same as the distance between the value 2 and value 3. The estimation of the intercept and the slopes of this variable are produced considering this assumption. However, conceptually this assumption is wrong, since ordinal variables are not scales, so there is no guarantee that the distances are the same.

By imposing several assumptions about normality, linearity, homoscedasticity, or independence of data for data analysis (^{Geurts, Irrthum & Wehenkel, 2009}), the General Linear Model approach demands a great deal of effort to deal with complex educational datasets. On the other hand, the rationale of the Regression Tree Method is effective in dealing with complex datasets because this is a data-driven approach (^{Gomes & Jelihovschi, 2019}). This method does not demand any assumption about the data, and this absence of assumptions makes it very suitable to deal with all types of variables, and all kind of linear and non-linear relationships among the variables (^{James et al., 2013}).

The CART algorithm is, probably, the most famous and used technique of the Regression Tree Method. It has been originated in the machine learning field (^{James et al., 2013}). This algorithm was created by ^{Breiman, Friedman, Olshen and Stone (1984}) to implement the Classification and Regression Tree Method. Since the CART algorithm is not part of the mainstream quantitative approaches in Education and Psychology, we shortly explain the principles of this technique. [See ^{Gomes and Almeida’s (2017}) as well Gomes and ^{Jelihovschi’s (2019}) papers for more detailed information about this approach, especially its application to educational data.].

The CART algorithm contains some attractive properties. For instance, this algorithm does not make any assumptions about data, which makes it very useful for discovering linear or non-linear relationships among the variables (^{Geurts et al., 2009}). It also allows for the presence of many types of predictors in its models, without the need of preparing or transforming the variables. Another advantage is that its outputs generate results that are easy to read and to interpret, making them understandable and accessible to decision makers, managers, educators, as well as the general public (^{Gomes & Almeida, 2017}).

In the case of regressions, the CART algorithm tries to reduce to the minimum possible the ordinary least squares error of the outcome prediction. To reduce this error, the CART algorithm divides the data into parts, and every data partition generates two new separated parts (^{Lantz, 2015}). The CART algorithm' output looks like a tree. The original data is named root node. The parts created by the algorithm through the splits of the data are named nodes, and the nodes that are not broken are called terminal nodes or leaves (^{Zhang & Singer, 2010}).

The process of data partition is complex. Every division of data is originated from the best split from a set of splits. For instance, for any partition of the data, the CART algorithm performs a specific split of that partition, for each value of every predictor. From these splits, the algorithm selects the best split, which is the split that reduces the most the outcome prediction error. The partition of the data is recursive and continues until it is no longer possible to decrease the outcome prediction error, or until another criterion is achieved, as for example, the minimum number of cases for each node.

As a result of this approach, the CART algorithm produces some data partitions that reduce the outcome prediction error only for the sample in question, but not for other samples, hindering the generalization of the results. The literature of machine learning recognizes this phenomenon and refers to it as overfit. To deal with overfit, the machine learning field recommends separating, randomly, the data in a training sample and a test sample, as well as to perform a cross-validation in the training sample (^{James et al., 2013}), and also to "prune" (name coined by the literature) some of the tree nodes created by the CART algorithm to help the generalization of the model or to facilitate the interpretability of the tree (^{Rokach & Maimon, 2015}).

The literature of machine learning suggests two different ways to carry out the process of pruning the tree: one is called complexity cost criterion, while the other use the interpretability criterion (^{Rokach & Maimon, 2015}). The complexity cost criterion identifies the number of tree nodes that generates the lowest outcome prediction error, pruning all the nodes that are beyond a given cut-off value. In turn, the interpretability criterion aims to maintain only a small amount of tree nodes, easy to interpret, as well as to generate substantial information, pruning all the other nodes (^{James et al., 2013}; ^{Rokach & Maimon, 2015}).

2. Comparing Regression Tree Model to Multiple Regression

In this article, we compare the Regression Tree Method to Multiple Linear Regression applying both in a predictive model with 53 predictors and the languages domain as the outcome of reading achievement. We apply Multiple Linear Regression because this technique is a very representative technique of the General Linear Model and largely applied in Education. All variables of the model come from the 2011 National Exam of Upper Secondary Education (Exame Nacional do Ensino Médio [ENEM]). Currently, ENEM is the measure by which the quality of the Secondary Education is evaluated, and it is also the main national assessment measure to select students for the entrance in Brazilian public universities, through the Unified Selection System (SiSU), as well as in some universities abroad (^{MEC/INEP, 2013}). Besides, if we consider the number of students who take the exam annually, the ENEM has a remarkable position in the world as an assessment for the entrance of students to Higher Education (^{Brasil/INEP, 2015}). Since 2009, the ENEM has 180 multiple-choice items and an argumentative essay measuring four broad domains: natural sciences, mathematics, human sciences, and languages, and it is administered once a year, over two days, to millions of students. Each year, the ENEM microdata collect, register and store demographic, socioeconomic, educational, and motivational information about the students who take the exam.

The ENEM microdata are composed by many and diverse variables (i.e. quantitative, nominal variables with many categories and ordinal variables) which are freely available for download by the INEP at http://portal.inep.gov.br/web/guest/microdados and are supported by the Brazilian Ministry of Education (^{MEC/INEP, 2012}). Some studies have applied the Regression Tree Method to predict academic achievement (i.e. ^{Pazeto et al., 2019}, ²⁰²⁰). Some of them applied this method in educational complex datasets, as the ENEM (^{Gomes, Amantes et al., 2020}; ^{Gomes & Jelihovschi, 2019}; ^{Gomes, Fleith et al., 2020}; ^{Gomes, Lemos & Jelihovschi, 2020}). However, concerning the ENEM, none of them have studied the suitable of the Regression Tree Method to construct educational evidence regarding the relationship between predictors and outcomes, in comparison to the General Linear Model. Our purpose, in this article, is to compare the Regression Tree Method and the Multiple Regression to empirically illustrate our argument that the Regression Tree Method is more adequate to construct evidence in complex educational datasets.

We believe the most important contribution of our article is to argue that the Regression Tree Method may be broadly applied in complex educational datasets. Additionally, we intend to show that the General Linear Model can be applied with important restrictions and cautious. We aim to challenge the almost exclusive use of the General Linear Model in complex educational datasets, inviting the researchers to use suitable alternatives.

3. Method

3.2. Variables of the analysis

Next, we briefly present the structure of our database and the variables of the analysis. The 2011 ENEM's microdata are comprised of seven parts or blocks of information: (1) Students’ data; (2) students’ school data; (3) municipality data, the place where the student took the exam; (4) multiple-choice exam data; (5) argumentative essay data; (6) basic education census data; (7) socioeconomic questionnaire (^{MEC/INEP, 2012}).

Table 1 Predictors of the study, which were extracted from the 2011 ENEM's microdata. 

The outcome variable of our study comes from the fourth block of information and it refers to the students' scores in languages domain, which comprises reading. The exam has 180 items and 45 items measure the language domain. This is a broad domain composed of 9 language competences and 30 abilities that are defined by a theoretical reference matrix. The students' languages scores derive from a standardized scale with a mean of 500 points and standard deviation of 100 points, ranging from 0 to 1000 points (^{Brasil/INEP, 2015}). This scale is produced by the Instituto Nacional de Estudos e Pesquisas Educacionais Anísio Teixeira (INEP), which is the Brazilian institute responsible for producing, storing, and making available to the public the ENEM' microdata. In turn, the 53 predictors of our study originate from the first, second, and the seventh block of the 2011 ENEM's microdata. All the predictors are outlined in Table 1. The reader can get more details about the ENEM and its microdata in ^{MEC/INEP (2012)}.

4. Results and discussion

The Regression Tree Method and the CART algorithm are not current approaches in Educational Sciences. So that, we will present and discuss the results together, focusing on the reading of the pruned tree, and showing how the structure of this tree can provide substantial information about the relationship between the predictors and outcome.

The CART algorithm generated a non-pruned tree with 32,131 leaves and 45,053 data splits. Many of these tree leaves only increase the outcome prediction error. The cost complexity criterion indicated that the first 2,074 leaves of this tree produced the lowest outcome prediction error (72.08%). Nonetheless, the cost complexity criterion suggested a pruned tree with still a very large number of leaves yet (2,074), leaving the tree with no interpretation and without any substantial information. Thus, we used the interpretability criterion to produce the final pruned tree. This remaining tree has only 13 splits and 14 leaves, and an outcome prediction error of 79.80%. Comparing this tree to the pruned tree indicated by the cost complexity criterion, there's a difference of only 6.72%, in terms of outcome prediction error favoring the cost complexity criterion. However, there is a difference of 2,060 leaves in favor of the final tree. Although this tree produced a relative worse outcome prediction, it allows the attainment of substantial information and interpretability. Therefore, our study resulted in this pruned tree with 14 leaves.

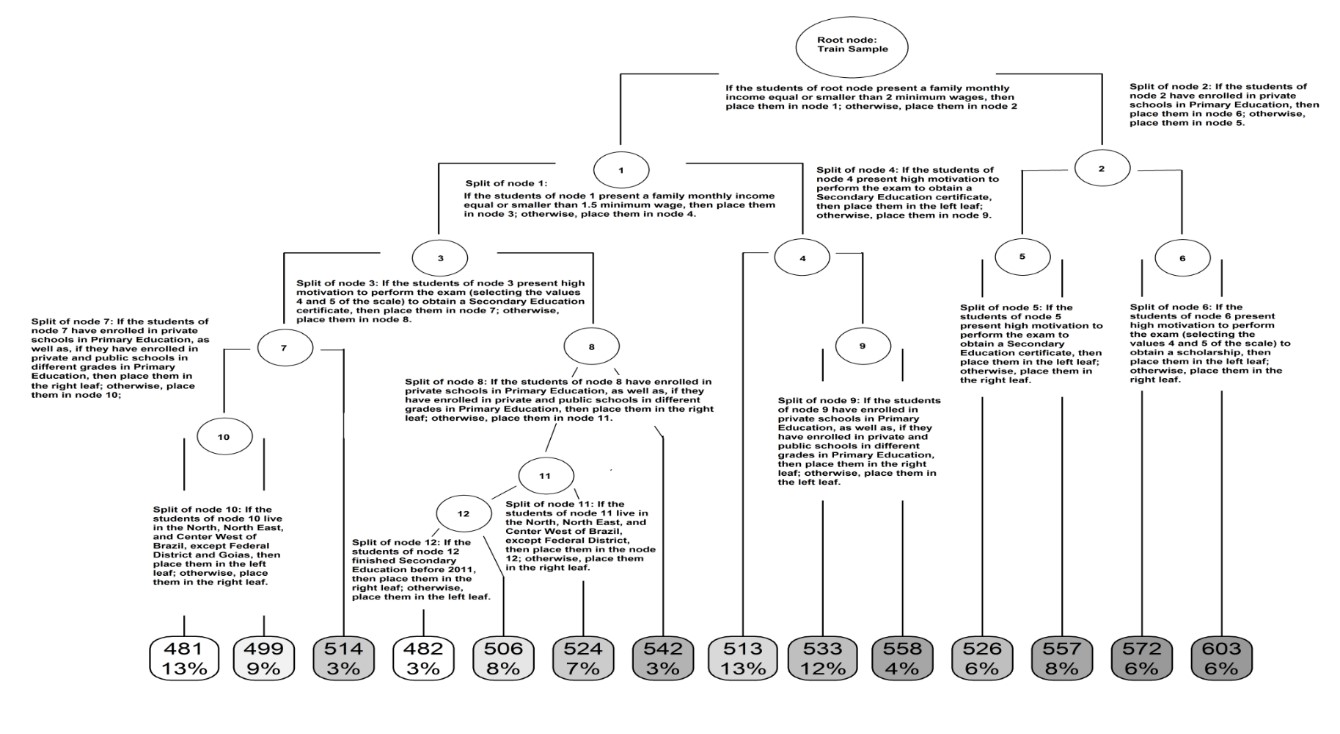
The final tree with 14 leaves explained 20.20% of the students' reading achievement variance in the training sample, as well as 20.14% of the students' reading achievement variance in the test sample. This small difference of 0.06% between the samples suggests a considerable generalization of the predictive model. The Figure 1 shows the pruned tree with 14 leaves. The root node is represented by the oval figure at the top of Figure 1. The nodes are represented by the numbered circles and the leaves (terminal nodes) are represented by the oval figures at the bottom of Figure 1. Every tree leaf in the Figure 1 has two numbers: The top number shows the reading average achievement of the students contained in the leaf, while the bottom number shows the percentage of the students in the training sample that belong to the leaf. For example, at the left corner of Figure 1 (taking the reader as reference), there is a leaf with the numbers 481 and 13%. These numbers indicate that this leaf is composed of students with an average of 481 points in reading achievement, which represent 13% of the training sample.

Figure 1 Pruned tree.  

Since every tree leaf is formed by a set of splits, which starts at the root node, we get information of each leaf by reading the tree through a top-down screening. For example, the leaf with 13% of the training sample and an average of 481 points in reading achievement, at the left corner of Figure 1, is the product of the splits of root node, node 1, node 3, node 7, and node 10. This leaf contains the students who: [1] have a family monthly income equal or smaller than 1.5 minimum wage (splits of root node and node 1), [2] show high motivation to perform the exam in order to obtain a Secondary Education certificate (split of node 3), [3] have not enrolled in private schools in Primary Education or attended private and public schools in different grades in Primary Education (split of node 7), and [4] live in the North, North East, and Center West of Brazil, except Federal District and Goiás State.

We now present the main results. Despite the large number of 53 predictors employed in the predictive model, we can observe in the Figure 1 that the CART algorithm used six predictors to produce the splits in the pruned tree. These variables are: [1] Students' family monthly income; [2] type of schools attended by students in Primary Education; [3] students' motivation to perform the exam to obtain a Secondary Education certificate; [4] students' motivation to perform the exam to obtain a scholarship; [5] student's home location: State in Brazil; and [6] completion of Secondary Education.

The most important variable used by the CART algorithm to discriminate students' reading achievement is students' family monthly income, as we can see in Figure 1, which is an indicator of socioeconomic status (^{OECD, 2019}). This variable of the ENEM microdata is an ordinal variable with a large number of categories that represent different intervals of income. The pruned tree shows that students with a family monthly income higher than 2 minimum wages cluster around the four leaves at the right corner of Figure 1; in general, these leaves (526 points, 557 points, 572 points, 603 points) have the greatest averages in reading achievement. In turn, students with a family monthly income between 1.5 and 2 minimum wages compose the three leaves with average of 513 points, 533 points, and 558 points, representing an intermediate achievement in reading. Students who present a family monthly income equal or smaller than 1.5 minimum wage compose the seven leaves at the left corner of Figure 1; overall, these leaves have the lowest averages in reading achievement. These results show that a family monthly income higher than 2 minimum wages is related to the highest averages in reading achievement, while a family monthly income between 1.5 and 2 minimum wages is related to intermediate averages in reading achievement, and a family monthly income smaller than 1.5 minimum wage is related to the lowest averages in reading achievement. By looking into this result, we observe that only a few categories of this predictor are relevant to discriminate the variance of the outcome. This result is striking because it shows that the General Linear Model’s assumption about the ordinal variables is incorrect for the analyzed data. It is not adequate to assume, as General Linear Model does, that all the values of ordinal variables have the same importance to explain the outcome variance. As the pruned tree shows, many categories of family income, particularly the higher intervals of income, have no significance. This outstanding result is an important parameter for the researcher’s interpretation of the relationship between the students’ income and reading achievement. Through this result the researcher can build evidence that only the lower income categories make any difference to differentiate the students’ reading variance. Consequently, the researcher can conclude that if public politics act on income, changing the small income brackets of Brazilian families can provide better opportunities for students to increase their achievement.

In spite of the students' family monthly income be the main predictor, it is not, by itself, a powerful enough predictor of students' reading achievement (Figure 1). For example, the leaf with an average of 533 points, which comprises the students' family monthly income between 1.5 and 2 minimum wages, shows a higher average performance than the leaf with an average of 526 points, which is associated with students' family monthly income higher than 2 minimum wages. Thus, other variables in addition to students' family monthly income account for the shared variance with reading achievement. Along our pruned tree (Figure 1), it can be observed that one variable that discriminates students' reading achievement besides students' family monthly income is students' motivation to perform the exam to obtain a Secondary Education certificate. This finding suggests that if a student shows high motivation to perform the exam to obtain a Secondary Education certificate, then her reading achievement tends to be lower compared to their counterparts who have medium or low motivation to perform that exam. Moreover, students' motivation to perform the exam to obtain a scholarship is a relevant variable, namely for those students whose family monthly income is higher than 2 minimum wages (split of root node) and have enrolled in private schools in Primary Education (split of node 2). These results might seem incorrect, at least superficially, since they affirm that more motivation leads to lower reading achievement. However, these findings make sense. In Brazil, the students who intend to take ENEM to obtain a certificate are those who did not finish high school in the expected time. These are students who have failed and had to repeat one or more years of their education. They usually have learning difficulties, as well as, lower academic achievement. Therefore, more motivation to take the ENEM to obtain the certificate implying less academic reading achievement is a result that makes sense in the Brazilian context. The same applies to the result which shows that more motivation to perform the exam to obtain a scholarship implies less achievement in reading, notably in family monthly income higher than 2 minimum wages. In Brazil, the scholarships are provided by the Brazilian government only for those students which have lower income and intend to enroll in private universities. In comparison, private universities have high costs while public schools are free. In addition, private institutions are less prestigious than public universities, which centralize research in Brazil. Hence, students need to get a high score on ENEM to enroll in public universities, while a low score is enough to enroll in almost all private institutions. Thus, students with low family income and low ENEM scores enroll in private universities hoping to get a scholarship from the Brazilian government. Even if they receive a scholarship, their family income must be higher 2 minimum waves, otherwise they are not able to pay the high costs of private universities, because scholarships tend not to cover all the costs (^{Gomes & Jelihovschi, 2019}).

Another very important aspect of the results regarding the predictors of motivation is the General Linear Model assumption involving the ordinal variables. As we can see in Figure 1, the values 4 and 5 are the substantial values to explain the variance of the outcome. The distances between 0 and 1, 1 and 2, 2 and 3 are not important, which supports the conclusion about family monthly income that only a few categories are indeed important. Both results show that the General Linear Model assumption about ordinal variables is very incorrect, at least for the analyzed data. This makes substantial difference when building evidence about the predictors and the outcome. Through the output of the pruned tree, the researcher can conclude that only the higher values of motivation to get a certificate or a scholarship make a difference in discriminating students’ reading performance. She can claim that more or less motivation at the lower values of motivation makes no difference, claiming that the relation between motivation and reading achievement is non-linear and seems to work like the activation of the neurons, in that one needs to greatly increase motivation to influence variation in reading achievement.

It is worth mentioning that the output of the pruned tree shows how predictors are conditioned by other predictors to predict the outcome. As we said, the students' motivation to perform the exam to obtain a scholarship is conditioned by the variable “family monthly income” and the variable “type of schools attended by students in Primary Education”. The General Linear Model is not able to provide this kind of evidence about the relationships between the variables. The Multiple Regression approach, for example, assumes that the predictors are unrelated, that is, orthogonal, so the weight of each predictor is added to the weight of the other predictors to explain the variance of the outcome. In a very different approach, the Regression Tree Method assumes that if a node is a product of ancestral nodes that were created by using distinct predictors, then this node indicates that a relationship exists between these predictors.

Another relevant variable to discriminate students' reading achievement is the type of school attended by students in Primary Education. The highest averages in reading achievement are related to the students who have attended only private schools (split of node 2), or at least, have attended a mix of private and public schools in different grades in Primary Education (split of nodes 7, 8 and 9). Furthermore, students who finished Secondary Education before 2011 (right leaf of split of node 12, with 506 points) tend to have a better performance than the students who did not finished Secondary Education before 2011 (left leaf of split of node 12, with 482 points). In turn, students who live in the South, South East of Brazil, or in the Federal District, tend to have a better performance (right leaf of split of node 10, and right leaf of split of node 11, with 499 and 524 points, respectively) than the students who live in other regions (left leaf of split of node 10, and leaves from the left node (node 12) of split of node 11, with 481 and 482 or 506 points, respectively).

We may conclude then, that two main properties regarding the relationship between the predictors and the outcome variable of students' reading achievement are important. The first represent the fact that some predictors are conditioned by other predictors in terms of their own predictive roles. For example, the completion of Secondary Education only discriminates the reading achievement of the students who: [1] have a family monthly income equal or smaller than 1.5 minimum wage (split of node 1), [2] present medium or low motivation to perform the exam to obtain a Secondary Education certificate (split of node 3), [3] neither enrolled in private schools in Primary Education, nor attended in private and public schools in different grades in Primary Education (split of node 8), and [4] live in the North, North East, and Center West of Brazil, except Federal District (split of node 11). Furthermore, the completion of Secondary Education does not have a predictive role in other contexts. This variable is neither for students whose family has a monthly income higher than 2 minimum wages, nor of students whose family has a monthly income between 1.5 and 2 minimum wages. This is an evidence of non-linear relationship among a set of predictors and the outcome. Another example of non-linearity among variables is the fact that the variable student's home location does not have any predictive role for the students whose family has a monthly income higher than 2 minimum wages, nor the students whose family has a monthly income between 1.5 and 2 minimum wages. Another striking result refers to the second trend: there are categories of some variables that are related to either worse or better reading achievement under specific conditions. For example, in the case of type of school attended by students, for those students who present a family monthly income higher than 2 minimum wages, only private schools are related to a better performance. On the other hand, for students who have a family monthly income equal or smaller than 2 minimum wages, a mix of private and public schools attended by the students in different grades in Primary Education is also related to a better performance. In other words, as Figure 1 shows, depending on the socioeconomic context, the type of school attended by students is related to a better or to a worse reading achievement. Another example: Goiás State is related to a better reading achievement in the context of node 10 split (499 points vs 481 points), and to worse reading achievement in the context of node 11 split (482 or 506 points vs 524 points). This is a very interesting result that is very unlikely to be achieved by General Linear Model techniques.

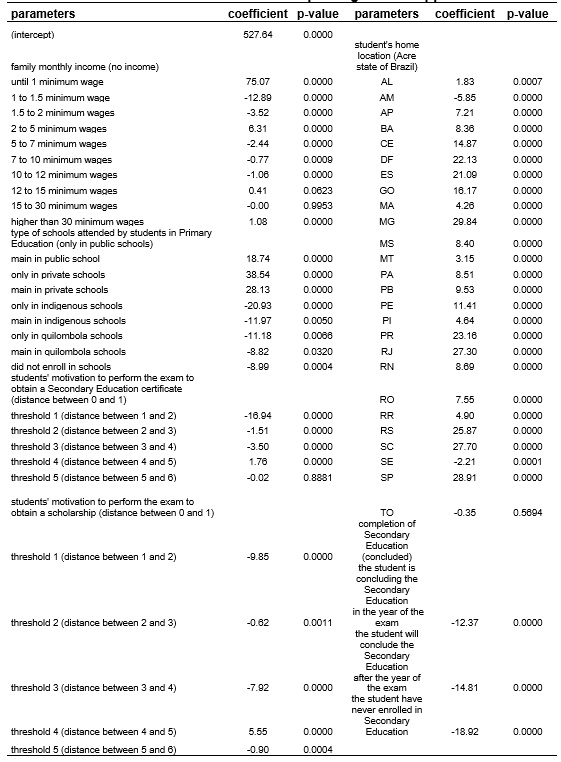
The results of the Multiple Regression technique are shown in Table 2. The intercept is 527.64, indicating that if all predictors have the value of their reference category, then the score of the students who took the 2011 edition of ENEM will have 527.64 points in reading.

All the results on the predictors corroborate what we have previously argued. As stated, the reference category of the family monthly income variable is “no income”. It is notable that the multiple regression result supports that if the family’s monthly income is up to 1 minimum wage, compared to a family with no income, then these students will score 75.07 points higher than students living in families with no income. Note in Table 2 that the distances between the categories are very unequal. According the General Linear Model assumption, the distances should be equal and either increase or decrease. The result shows a very different pattern, that is, a non-linear shape. Some categories indicate a better reading achievement compared to the reference category, while other categories show lower reading achievement. As we said, even creating dummy variables for ordinal variables, as we did, this is not very appropriate, since the researcher is asked to compare all the categories only in against the reference category. Therefore, in our case, we can only compare the categories with respect to the reference category “no income”. We do not know anything else.

What is observed in the ordinal variable family monthly income also occurs in the nominal variable type of schools attended by Primary Education students. The reference category is students who enrolled only in public schools. The results show that the largest increase for this reference category is of 38.54 points in reading achievement, relative to the category of students enrolled in private schools only. The results also show that if students enrolled in any year in private school, then their reading achievement is better than that of the students who are only enrolled in public schools. On the other hand, if students enrolled in any other type of schools besides private and public schools, then these students have lower reading achievement. Note that all results are about the categories compared to students enrolled in public schools only. If the researcher wants to compare other interesting relationships between other categories, she is not able to do that.

Table 2 Results from the Multiple Regression Approach. 

Regarding students’ motivation to take the exam to obtain a high school certificate, the results of the regression model show that the only relevant distance between the values is the one covering values 1 and 2. If the students move from value 1 to 2, their achievement in reading have a reduction of 16.94, compared to students moving from value 0 to 1. The other distances imply small reductions, and the distance between value 4 and 5 implies an increment in the achievement score. This indicates a non-linear relationship between this predictor and the outcome. A similar finding is observed in the motivation of students to take the exam to obtain a scholarship.

Regarding the nominal variable completion of Secondary Education, the results indicate that if the students do not complete high school before taking the exam, they will have a worse reading achievement, compared to students who have completed high school. As for the nominal variable of students’ location, the results show that only those living in the states of Sergipe and Amazonas are related to a worse reading performance, compared to the Brazilian state of Acre (p < .05). In addition, students living in Minas Gerais will score 29.84 points higher in reading achievement than students living in Acre.

5. Conclusions

In this article, we presented the advantages of the Regression Tree Method, compared to the General Linear Model, for building evidence on complex educational datasets. Our comparison found many substantial non-linear relationships between the predictors and the outcome. In addition, we show why the logic of the General Linear Model is inadequate to handle non-linear relationships. Not dealing adequately with non-linearities makes the evidence fragile, since non-linear relations tend to change the results considerably, as well as, the scientific narrative that the researcher will hold about the data.

We also show that the General Linear Model is not the best idea when it comes to complex educational datasets. Unfortunately, its use is very dominant in Education and complex educational datasets. We hope that researchers will understand that the use of the General Linear Model should be applied to complex datasets only under special conditions. Taking our data as example, if a researcher argues that her interest primarily involves observing how the other categories of each ordinal and nominal predictors are related to a specific reference category of each predictor in which she has a theoretical interest, then the General Linear Model may be a reasonable approach. However, this goal is very restrictive and it is not the rule when the researcher intends to use a quantitative method. Typically, the researcher wants the method to be able to provide her with some substantial results about the relationships between various categories of nominal and ordinal variables, if these types of variables are present in the predictive model. In addition, the researcher wants the method to be able to provide a suitable approach to discovering complex non-linear relations, if they are relevant and represent important pattern in the data. For example, the pruned tree showed us that living in Southern, Southeastern of Brazil, or the Federal District, and having completed high school before ENEM 2011, showed only a predictive role for reading achievement in the context of the poorest families, who had a family monthly income of 1.5 minimum wages or less. This striking evidence is surprising and difficult to find by the General Linear Model. It substantially undermines scientific knowledge about how predictors are associated with outcomes and thus their effects on public policy and leads to inappropriate educational interventions. Imagine that you are an educational manager or an educational researcher and you discover that there is a non-linear relationship among type of school, family income and reading achievement. Also, suppose that you found that for the students who have a family monthly income higher than 2 minimum wages, only private schools predicted a better performance in reading. On the other hand, for the students who have a family monthly income equal or smaller than 2 minimum wages, a mix of private and public schools attended by the students in different grades in Primary Education predicted a better performance. Will this finding change your knowledge about reading and some factors that may affect this result producing substantial evidence? We found this result in our analysis only because we applied the Regression Tree Method. If we had used only Multiple Regression, we would not have found it.

Like many other studies, in spite of their originality and relevance, our study has some limitations that need to be considered. We did not simulate the data to be analyzed. We used an empirical data set to illustrate our arguments. Therefore, new studies could be interesting to corroborate or refute our arguments through simulation studies. However, although our data are not simulations, they do represent complex educational datasets everywhere, and not only in the Brazilian context. Our data is abundant in nominal and ordinal variables with many categories, just as our data seem to be abundant in non-linear relationships among variables. Although our goal was to use the data as an illustration to enrich our argument about the advantages of the Regression Tree Method, as compared to the General Linear Model, for analyzing complex educational datasets, we believe that our data, if not perfect as a simulation, was sufficient. Another possible limitation is that we only used Multiple Regression as a technique of the General Linear Model. We could apply a large number of techniques from this model to obtain more robust evidence. However, as we said, the Multiple Regression approach is the most widely used technique and represents well the logic of the General Linear Model. Therefore, we believe that using only Multiple Regression was not a problem and did not compromise our results and conclusions.

Our study has found evidence that highlights the relevance of investing in data-driven approaches, capable of discovering relevant non-linear relations that are hindered in the use of techniques from the General Linear Model. We hope see, in a short range of time, the Regression Tree Method pertaining to the techniques of the mainstream approaches in Education, especially in the context of the complex educational datasets.