Polynomial Method for the Calculation of Corrosion Parameters in a System with Mixed Control

M. Guzman^a,* , R. Lara^a and G. Garay^b

^a Universidad Catolica del Norte, Facultad de Ciencias, Departamento de Quimica, Angamos 0610, Antofagasta-Chile

^b Universidad Catolica del Norte, Facultad de Ciencias, Departamento de Matematicas. Angamos 0610, Antofagasta-Chile

 

Abstract

An algorithm is presented for the calculation of corrosion parameters with mixed charge-transfer and diffusion control, based on the polynomial method, and having good accuracy and precision.

Keywords: polynomial method; mixed-control; corrosion parameters; electrokinetic parameters.

 

Introduction

Several algebraic and computational methods have been developed [2-12] for the calculation of corrosion parameters derived from the Wagner-Traud [1] equation for a corrosion system controlled by charge transfer. Nevertheless, the case of mixed charge transfer and diffusion control has been little studied. The most important equations related to this situation are those of Nagy [13], for describing the cathodic diffusion reaction, and the El-Fecki [14] equation related to the anodic and cathodic reactions. The polynomial method has been used for calculating corrosion and electro kinetic parameters [11, 15] in systems controlled only by charge transfer.

The goal of the present study is to apply the polynomial method to resolve the corrosion parameters in a system with mixed control of charge transfer and diffusion of the cathodic reaction.

 

Experimental

The effect of mass transport in the determination of corrosion parameters obtained from polarization data is given by the equation of mixed polarization control obtained by Nagy [13]

 

 

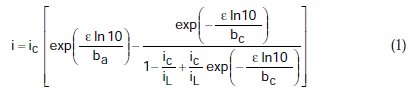
where, i = current density, ic = density of corrosion current, iL =density of limiting cathodic current, e = polarization, ba = anodic Tafel slope, and bc = cathodic Tafel slope. This general equation describes the polarization curve for the case in which the cathodic reaction is under the control of mass transfer (ic = iL), mixed control (iL > ic), and control of charge transfer (iL = ∞). In the following, for simplicity, we use ic/iL = r.

Equation (1) can be developed according to the Maclaurins series, following which, and ordering the terms, we obtain:

 

 

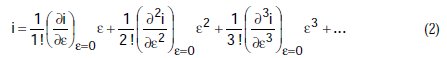
If we divide by e the preceding equation is transformed to:

 

 

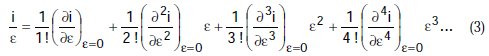
Equation (3) is a polynomial, and may be simplified to:

 

 

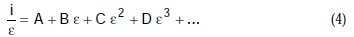
where A, B, C, D are known constants for a given system, equal to:

 

 

 

 

 

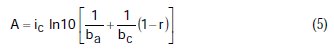
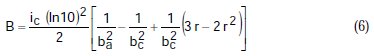
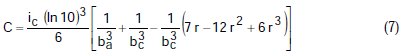
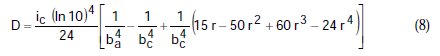
To obtain the corrosion parameters ic, r, ba, and bc from the Nagy equation, even though there are four equations and four unknowns, since these equations are not linear, it was necessary to employ a mathematical program, which, in the present case, was maple18.

 

Results and discussion

Test method artificial data

In order to test the methodology we generated artificial data on polarization, Table 1, with four significant figures, provides the corrosion density, r and Tafel constants for Equation (1).

 

 

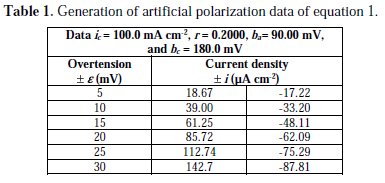
Using the Polynomial method, and with the help of the mathematical program above cited, parameters for this initial equation are calculated. Through polynomial regression of i/e versus e, we obtain the polynomial equation:

 

 

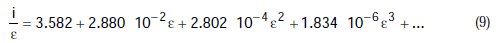
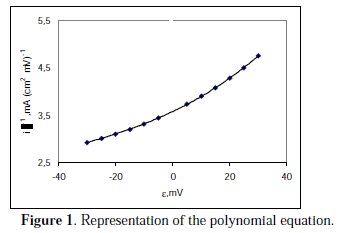
There is a correlation coefficient of R2=1.000, the graphic representation of which is shown in Fig. 1.

 

 

Taking the constants from the preceding polynomial, we obtain four equations:

 

 

 

 

 

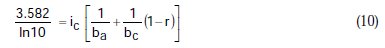
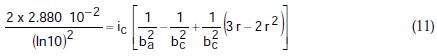
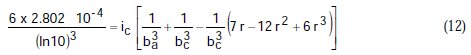
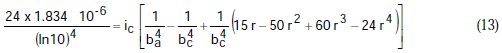
Using the non-iterative maple18 mathematical program, the results are: ic = 100.0 mA/cm²; ba = 90.00 mV; bc = 180.0 mV y r = 0.2000. These results suggest that the solution of the equation is adequate, since they are the same as the initial ones (Table 1), and therefore, the polynomial method resolves the mixed control equation (Equation (1)).

Testing the method with experimental data

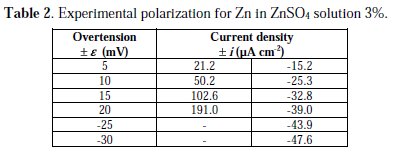
With the purpose of testing the method with experimental data, the data obtained by LeRoy [16] for the polarization of Zn electrode in a solution of ZnSO4 3% at 30 °C were chosen, as shown in Table 2.

 

 

Through polynomial regression of i/e versus e, we obtain the polynomial equation:

 

 

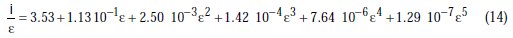
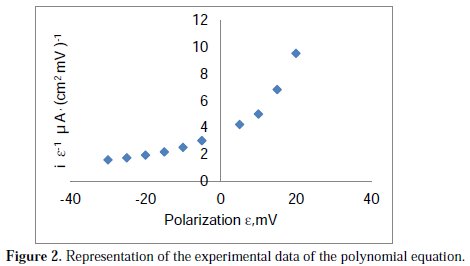
with a correlation coefficient of R2=1.000, the graphic representation of which is shown in Fig. 2.

 

 

Taking the constants from the preceding polynomial, we obtain four equations:

 

 

 

 

 

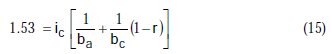
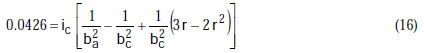
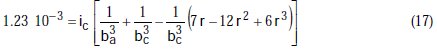
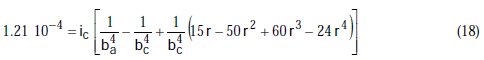
The results of corrosion parameters in the mixed system obtained using the non- iterative maple18 mathematical program, are shown in Table 3.

 

 

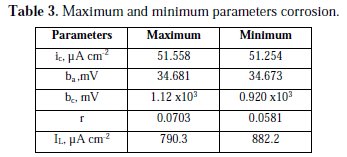
Parameters results show high sensitivity, whose extreme values are very similar. The very large cathodic Tafel slope indicates that the control is mixed. The anodic Tafel slope is the normally found for this system; the process controlled by activation is approximately 30 mV. The cathodic Tafel slope is very large, due to the reduction of oxygen, which is limited by the diffusion of oxygen.

This same system, using the polynomial calculation method for a corrosion system controlled by charge transfer [11], has delivery values for ic 51.5 μA cm^-2, ba 34.7 mV and bc 1.02 10³ mV; this is a high value, which also indicates that there is mixed charge-transfer and diffusion control.

 

Conclusions

It can be concluded that the non-iterative polynomial method, which is able to employ data obtained either by potentiostatic or galvanostatic techniques, can also be used for the calculation of corrosion parameters in mixed-charge transfer and diffusion control with high precision and accuracy.

 

References

1. Wagner C, Traud W. Z Elecktrochem. 1938;44:391.         [ Links ]

2. Barnartt S. Electrochim Acta. 1970;15:1313.         [ Links ]

3. Mansfeld F. Corrosion. 1973;29:397.         [ Links ]

4. Janskowski J, Juchniewicz J. Corros Sci. 1980;20:841.         [ Links ]

5. Bandy R. Corros Sci. 1980;20:1017.         [ Links ]

6. Greene ND, Gandhi RH. Mater Perform. 1982;21:34.         [ Links ]

7. Feliu V, Feliu S. Corrosion. 1986;42:151.         [ Links ]

8. Jensen M, Britz D. Corrosion. 1990;46:111.         [ Links ]

9. Guillen M, Guzman M, Lara R. Bol Soc Chil Quim. 1995;40:427.         [ Links ]

10. Guzman M, Ortega P, Vera L. Bol Soc Chil Quim. 1998;43:461.         [ Links ]

11. Guzman M, Ortega P, Vera L. Bol Soc Chil Quim. 2000;45:191.         [ Links ]

12. Barbato S, Alvarez M. J Chil Chem Soc. 2005;50:739.         [ Links ]

13. Nagy Z, Thomas DA. J Electrochem Soc. 1986;133:2013.         [ Links ]

14. El-Fecki AA, Walter GW. Corros Sci. 2000;42:1055.         [ Links ]

15. Guzman M, Ortega P, Vera L. J Chil Chem Soc. 2006;51:821.         [ Links ]

16. LeRoy R. J Electrochem Soc. 1977;124:1006.         [ Links ]

 

Acknowledgements

The authors thank Universidad Catolica del Norte for its economic support.

 

^*Corresponding author. E-mail address: mguzman@ucn.cl

Received April 21, 2016; accepted December 20, 2016

www.peacta.org