1. Enquadramento teórico

Ao longo das últimas quatro décadas diversos investigadores têm-se debruçado sobre as potencialidades da HM no ensino e na formação de professores (e.g. ^{Arcavi et al., 1982}; ^{Isaacs et al., 2000}; ^{Jankvist et al., 2019}; ^{Mosvold et al., 2014}; ^{Pinto & Costa, 2020}; ^{Schubring et al., 2000}; ^{Siu, 1997}; ^{Swetz, 1994}). No início da década de 80 do séc. XX já se pensava que “maybe a mathematics teacher can profit from the study of the history of mathematics” (^{Arcavi et al., 1982}, p.30). O grupo HPM - The International Study Group on the Relations between the History and Pedagogy of Mathematics - desde 1976 um afiliado do ICMI - International Comission on Mathemathical Instruction -, agrega a maioria dos investigadores nesta área, tendo também uma atuação dinamizadora através de encontros internacionais bianuais, da difusão das publicações (em (^{HPM, 2021})) é possível aceder à maioria do corpo científico produzido no âmbito da sua atuação), entre outros.

Uma discussão recorrente que tem acompanhado a investigação nesta área é a discussão sobre os diferentes modos de utilizar a HM no ensino (^{Katz, 2004}; ^{Swetz et al., 1995}; ^{Tzanakis & Arcavi, 2000}). Por exemplo, em Portugal, a Associação de Professores de Matemática publicou, pouco tempo depois da publicação de (^{Swetz et al., 1995}), a tradução de três artigos dessa obra, (^{GTHEM, 1997}), que refletiam sobre as vantagens da utilização da HM no ensino, mostrando que esta corrente era acompanhada em Portugal. Os títulos desses artigos são ilustrativos das questões que se colocavam aos investigadores: “Porquê estudar a História da Matemática?” (Struik), “A utilização da História em Educação Matemática” (Fauvel) e “Quer dar significado ao que ensina? Tente a História da Matemática” (Swetz).

Em 2004, Katz publicou uma obra de referência na HM, com a particularidade de incluir um apêndice dedicado à sua aplicação ao ensino. Este apêndice (Katz, 2004, pp. 521-524) é muito informativo pois faz a ligação entre conteúdos matemáticos comuns no ensino da disciplina com os diferentes momentos e os diferentes povos da HM que, de algum modo, contribuíram para a descoberta e desenvolvimento desses mesmos conteúdos.

Anos mais tarde, Jankvist apresentou uma sistematização da utilização da HM na educação fazendo uma “categorization of the 'whys' and 'hows' of using history in mathematics education” (^{Jankvist, 2009a}). O autor aponta duas categorias para a utilização da HM no ensino: (i) a HM como ferramenta para ensinar outros conteúdos e (ii) a HM como objetivo em si própria. Na segunda categoria, este autor apresenta um estudo aprofundado na sua tese de doutoramento “Using History as a “Goal” in Mathematics Education” (^{Jankvist, 2009b}).

Em Portugal, as orientações oficiais vão no sentido da categoria (i), ainda que as referências à HM e à sua utilização como ferramenta na prática de ensino nos programas, desde o EB ao ES, tenham vindo a diminuir. Os programas de Matemática de 1991 e 1997 valorizavam bastante a HM. Desde então, no programa para o EB, a tendência foi diminuir a referência à HM, desaparecendo no programa de 2013 e no ajustamento de 2018. O Programa e Metas Curriculares de Matemática do ES (2015/2016) apresentam menção explícita à HM em alguns descritores das Metas, indicando o uso da HM para enquadrar de um ponto de vista histórico os conteúdos abordados, bem como ilustrar a forma como a Matemática foi construída ao longo dos tempos e contribuir para uma compreensão mais profunda do pensamento científico.

Para além do modo como utilizar a HM no ensino, também o “como fazer” é uma questão essencial na investigação na área. Nesta última, há que atender a duas dimensões: por um lado, as práticas dos professores, e a existência de formação específica na área; por outro, as conceções dos professores sobre o potencial didático da HM.

Diversas investigações recentes a nível internacional dão contributos para esta discussão. Clark apresenta highlights de desenvolvimento da área de investigação, bem como diversos exemplos de aplicações práticas da HM no ensino (na Dinamarca, no Brasil e nos Estados Unidos) (^{Clark, 2019}); em (^{Clark et al., 2016}) efetua-se uma resenha, desde o ano 2000, das investigações que abordam as questões essenciais nesta área: Que história é adequada, pertinente e relevante para a Educação Matemática (EM)? Que papel pode a HM desempenhar em EM? Até que ponto a HM tem sido integrada em EM (currículos, livros didáticos, material de apoio/recursos educativos, formação de professores)? Como pode este papel ser avaliado e em que medida contribui para o ensino e aprendizagem da Matemática?; em (^{Barbin et al., 2018}) apresentam-se dez experiências que introduzem uma perspetiva histórica na sala de aula de Matemática (para alunos entre os 11 e os 18 anos); e Lim & Chapman relatam efeitos positivos do uso da HM nas atitudes, ansiedade, motivação e aprendizagens dos alunos de uma turma do 11.º ano (^{Lim & Chapman, 2015}).

Em Portugal, os trabalhos de investigação nesta área surgem, maioritariamente, através de dissertações de mestrado e teses de doutoramento; em vários casos os investigadores são professores de Matemática e entusiastas da HM, o que os leva a focar as suas investigações na aplicação ao ensino de temas da HM. Em (^{Neves, 2007}) são apresentadas tarefas para a utilização da HM na sala de aula, enquanto que nos estudos de doutoramento (^{Gil, 2012}; ^{Gonçalves, 2011}; ^{Tavares, 2016}) são apresentados estudos de caso em que tarefas com HM foram aplicadas em contexto de sala de aula no EB. ^{Jorge (2008}) “apresenta e avalia um Percurso de Formação com foco na História da Matemática, em que a resolução e exploração didáctica de problemas históricos foram encarados como uma metodologia a privilegiar na formação inicial de professores para o ensino básico” (p. iv).

Man-Keung Siu apresenta uma das primeiras tentativas de quantificar a opinião e a utilização que os professores fazem da HM (^{Siu, 2007}). A partir de 608 inquéritos realizados a professores de Hong Kong, a investigação efetuada estabeleceu os principais motivos apontados pelos professores para não utilizar a HM na sala de aula: “Não tenho tempo para isso durante as aulas” (67%); “Existe pouco material disponível nesse tema” (64%) e “Existe pouca formação de professores nessa área!” (83%).

2. Experiência de formação

A experiência de formação decorreu no âmbito da OF “Temas transversais nas Aprendizagens essenciais da Matemática”. Esta teve como objetivo conhecer, manejar e explorar os domínios inerentes às Aprendizagens Essenciais da Matemática, tendo em conta o Perfil do Aluno à saída da escolaridade obrigatória. Neste contexto, trabalharam-se os temas transversais - Resolução de Problemas, História da Matemática e Modelação Matemática - integrados nos programas da disciplina de Matemática do ES, com vista à elaboração e resolução de tarefas matemáticas. Pretendeu-se, ainda, promover o trabalho colaborativo entre os professores e a partilha de experiências didáticas, sem descurar a discussão e adequação das diferentes modalidades previstas para avaliação dos alunos, promovendo articulação curricular.

Os temas matemáticos trabalhados, com ênfase no papel da HM no processo ensino/aprendizagem, foram: Lógica e conjuntos (Álgebra de Boole); geometria (geometria euclidiana vs geometrias não euclidianas, Descartes e a geometria analítica); polinómios e funções polinomiais (equações do 2.ºgrau, segundo Pedro Nunes; Galois e a resolubilidade algébrica de equações); funções exponenciais e funções logarítmicas (do problema das tangentes ao cálculo diferencial; breve história dos logaritmos; breve história do número de Neper); números complexos (breve evolução histórica). Focou-se a transversalidade dos tópicos e a articulação da Matemática com outras ciências/áreas do conhecimento (abordou-se a álgebra de Boole e a conceção de circuitos elétricos; em Geometria, trabalhou-se a geometria do planeta Terra). Fez-se uso de recursos diversificados, entre os quais textos originais em HM, em articulação com tecnologias de apoio (calculadora gráfica, na resolução da equação cúbica; uso de Ambientes de Geometria Dinâmica (AGD), para tratar problemas “antigos”, como o quinto postulado da geometria de Euclides e a origem da geometria hiperbólica ou a noção de distância de Manhattan).

A OF foi desenvolvida intercalando sessões presenciais conjuntas (25 horas) com trabalho autónomo dos formandos (25 horas). As sessões presenciais foram ponto de partida e de chegada do trabalho autónomo dos formandos, articulando a teoria e a prática de sala de aula. Para os temas mencionados foi proposta a exploração de tarefas conducentes à produção de materiais, tendo em conta a transversalidade dos tópicos e as aplicações das diferentes áreas. Estes materiais foram aplicados em sala de aula e as reflexões sobre a sua aplicação feitas em grupo. Os passos metodológicos privilegiados foram: (i) diagnóstico das conceções e práticas dos formandos sobre conteúdos e temas transversais na aprendizagem da Matemática; (ii) pesquisa e listagem de recursos facilitadores da aprendizagem disponíveis on-line; (iii) planificação e produção de tarefas/materiais/recursos pedagógicos; (iv) reflexão em grande grupo sobre a implementação de estratégias de ensino e aprendizagem, bem como dos materiais produzidos e sinalizados; (v) reformulação de estratégias e materiais produzidos, em resultado da sua implementação; (vi) apresentação de resultados, seguida de debate, com vista à reflexão sobre o trabalho produzido; (vii) apresentação e debate dos trabalhos realizados, reflexão final de avaliação e balanço da OF.

O período da formação coincidiu, em grande parte, com o período de confinamento decretado em março de 2020, devido à pandemia de COVID 19, durante o qual funcionou o regime de ensino a distância. Tratando-se de uma OF, e ainda que em aulas em formato diferente do usual, os formandos implementaram algumas das propostas realizadas em grupo, recorrendo a guiões orientados e resumos sobre assuntos.

3. Métodos

O estudo tem uma natureza mista, combinando uma vertente quantitativa (predominante) com uma vertente qualitativa. Esta opção resulta dos objetivos delineados para o estudo e do contexto em que este ocorre (^{Bardin, 2002}; ^{Creswell, 2007}; ^{Gall, Gall, & Borg, 2003}).

Os participantes no estudo são 16 dos 18 professores de Matemática que frequentaram e concluíram a OF, a qual decorreu entre março e maio de 2020. Os professores lecionam na região Braga, a maioria dos quais (96%) nos 3.º CEB ou ES. A sua idade média é de 51 anos, o tempo médio de serviço docente é de 27 anos e 75% dos professores são do género feminino. A maioria dos professores (88%) possui licenciatura (destes, 71% com licenciatura em Ensino da Matemática), 8% possui mestrado (em Educação, com especialização em Supervisão) e 8% doutoramento (em Matemática).

A recolha de dados assentou na aplicação, on-line, de um questionário (Q) no início e no final da formação, com o objetivo de recolher informação que permitisse caracterizar: (i) a sua formação em HM; e (ii) as suas conceções e práticas sobre o uso da HM, antes e após a formação. Dois dos 18 professores não preencheram o questionário no final da formação e em outros quatro não foi possível emparelhar os questionários do início e do fim, pelo que não foram considerados na análise. O questionário está organizado em três secções relativas às dimensões do estudo: formação dos professores em HM (4 perguntas), conceções dos professores sobre HM (6 perguntas) e práticas dos professores no uso da HM na sua prática letiva (2 perguntas). Em cada uma das secções havia perguntas de resposta fechada, com escala de 1 (concordância mínima) a 4 (concordância máxima), e perguntas de resposta aberta, predominando as primeiras. Para além do questionário, recorreu-se também a notas de campo (NC) tomadas pela investigadora/formadora e a registos documentais (RD) produzidos pelos professores, nomeadamente uma apreciação da OF, produzida na última sessão.

Tendo esta investigação uma natureza mista, na análise de dados recorreu-se a técnicas de análise estatística e de análise de conteúdo. Em termos quantitativos, efetuou-se uma análise descritiva dos dados recolhidos na aplicação do questionário nos dois momentos, recorrendo a frequências e medidas de estatística descritiva. Na avaliação da representatividade da média utilizou-se o coeficiente de variação (CV) (a média será tanto mais representativa quanto menor o valor de CV; para CV>50% considera-se que a média não é representativa) (^{Afonso & Nunes, 2010}). Procedemos, também, a uma análise comparativa, item a item, dos resultados em dois momentos (no início e no final da formação), recorrendo ao teste de Wilcoxon, um teste de hipóteses não paramétrico. Neste estudo, conclui-se a existência de evolução significativa, do primeiro para o segundo momento, para p<.05 (significância de 5%). Para os cálculos, foi usado o software IBM® SPSS, versão 27.

Em termos da análise de conteúdo, analisaram-se as respostas dos professores às questões de resposta aberta, apreciações à formação realizada e notas de campo da formadora/investigadora.

Esta análise incidiu sobre três temas e respetivas categorias de análise (Tabela 1).

Tabela 1 Temas e categorias de análise 

4. Resultados

4.2 Conceções dos professores sobre o uso de HM para ensinar

As conceções dos professores quanto ao uso da HM são apresentadas na Tabela 2, organizadas em potencialidades e constrangimentos.

Tabela 2 Médias de concordância dos professores sobre as potencialidades do uso da HM na aula de Matemática ( x i , x f ), coeficientes de variação ( 𝐶𝑉 𝑖 , 𝐶𝑉 𝑓 ), no início e final da formação, e valor-p (p). 

No início da formação, os professores apreciaram de forma bastante positiva as potencialidades da HM (80% a 100% níveis 3/4; médias entre 2.9 e 3.6 pontos, representativas do conjunto de dados). Destacam-se a desmistificação da Matemática como um produto acabado e ilustrar a utilidade e importância da Matemática (100% níveis 3/4; médias 3.6 e 3.5). O item com menor pontuação foi ilustrar relações da Matemática com outras disciplinas (mais de 80% níveis 3/4; média 2.9).

Após a formação, os itens com melhores pontuações mantiveram-se. A avaliação global dos itens melhorou (100% níveis 3/4; média geral passa de 3.3 para 3.6, mantendo-se representatividade das médias). O maior aumento na média foi no item ilustrar relações da Matemática com outras disciplinas (0.6). De realçar, também, o acréscimo (0.3) nas médias da abordagem à Matemática diferente do usual e da ilustração de relações entre diversos domínios matemáticos.

Pelo teste de Wilcoxon, é possível concluir que os professores, no final da formação, reconhecem de forma mais significativa o potencial do uso da HM na aula de Matemática, ao nível da ilustração de relações da Matemática com outras disciplinas (p=0.035).

O reconhecimento da potencialidade da HM, enquanto recurso didático, é ilustrado pela seguinte afirmação:

Foi maravilhoso poder mergulhar no passado e percorrer as vivências de inúmeros matemáticos, que contribuíram para o desenvolvimento de todas as tecnologias, da ciência, afim da humanidade, apesar de todas as suas limitações, sobretudo em termos técnicos […] Neste momento, valorizo muito mais […] Este valor e agradecimento que devemos ter para com quem lutou e contribuiu para a evolução e desenvolvimento das nações, deverá ser passado aos nossos alunos. (RD_P2).

Apresentamos na Tabela 3 as perspetivas dos professores relativamente aos constrangimentos ao uso da HM nas suas aulas.

Tabela 3 Médias de concordância dos professores sobre os constrangimentos do uso da HM na aula de Matemática ( 𝑥 𝑖 , 𝑥 𝑓 , 𝑥 𝑖𝐶𝑎𝑡 , 𝑥 𝑓𝐶𝑎𝑡 ), coeficientes de variação ( 𝐶𝑉 𝑖 , 𝐶𝑉 𝑓 ), no início e final da formação, e valor-p. 

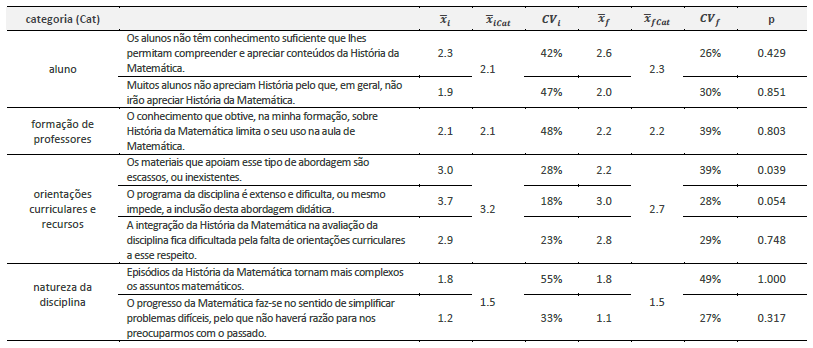
No início da formação, os maiores constrangimentos incluíam-se na dimensão orientações curriculares e recursos (média 3.2), destacando-se claramente a extensão do programa (mais de 90% níveis 3/4; média 3.7), seguida da escassez de materiais e da integração da HM na avaliação. Os constrangimentos com menor relevância tinham que ver com a natureza da disciplina (média 1.5, com representatividade pouco significativa).

Após a formação, os professores continuam a identificar como maiores constrangimentos aqueles relacionados com orientações curriculares e recursos (média 2.7), ainda que com decréscimos muito acentuados em escassez de materiais e programa da disciplina (0.8 e 0.7). Nas suas avaliações finais, identificaram, ainda, o excesso de tarefas burocráticas como limitador à pesquisa e conceção de propostas didáticas. Os professores passaram a julgar o conhecimento insuficiente dos alunos como um constrangimento mais relevante (acréscimo de 0.3 na média). A dimensão natureza da disciplina não sofreu alterações significativas.

De notar que o constrangimento formação do professor não é relevante para os professores (médias 2.1 e 2.2). Globalmente, as médias tornaram-se mais representativas.

O teste de Wilcoxon permite concluir que os professores, no final da formação, reconhecem, de forma mais significativa, a existência de materiais para o uso da HM (p=0.039).

4.3 Práticas dos professores de uso da HM para ensinar

Uma larga maioria dos professores (83%) referiu, no início da formação, utilizar a HM como recurso didático, aumentando esse nível para 100%, após a formação. Progresso semelhante admitem quanto à frequência desse uso (algumas/muitas vezes): inicialmente, 60%; após a formação, 92%. A tabela 4 apresenta resultados relativamente aos recursos mobilizados no uso da HM na aula de Matemática

Tabela 4 Médias de concordância dos professores sobre recursos mobilizados no uso da HM na aula de Matemática ( 𝑥 𝑖 , 𝑥 𝑓 ), coeficientes de variação ( 𝐶𝑉 𝑖 , 𝐶𝑉 𝑓 ), no início e final da formação, e valor-p. 

No que se refere ao uso de recursos em práticas de ensino recorrendo à HM verificou-se, no início da formação, uma predominância clara do manual escolar (100% níveis 3/4; média 3.3), seguido de textos/vídeos/sítios da web (mais de 90% níveis 3/4; média 3.1). Os recursos menos utilizados foram jogos antigos, instrumentos antigos e material didático elaborado pelo professor (médias 1.6; 1.7 e 1.8), itens cujas médias são menos representativas.

No final da formação é de assinalar a grande diminuição do uso do manual escolar (decréscimo 0.4 na média). Indicadora de uma dependência profunda desse recurso (que deixa pouco espaço à criatividade) é a seguinte avaliação:

apesar da sensibilização e do interesse que tive desde a formação inicial (que já vai longe!) pela História da Matemática […] tenho caído, em muitos momentos, na rotina que conduz à apresentação da matemática como um corpo de conhecimentos acabado e “compendizado” (RD_P2).

Os maiores aumentos nas médias verificaram-se nos itens material didático elaborado pelo professor, biografias de matemáticos e jogos antigos (0.9; 0.6 e 0.5).

O teste de Wilcoxon permite confirmar que os professores passaram a reconhecer, de forma mais significativa, do início para o final da formação, a utilização da HM através de materiais didáticos elaborados pelo professor (p=0.039). Para além disso, assumem valorizar menos o uso do manual escolar (p=0.044).

Os registos recolhidos evidenciam consenso quanto ao benefício do uso diversificado de recursos, quer ao nível de textos originais como integração de ferramentas tecnológicas. Disso é exemplo a seguinte afirmação:

As inúmeras pesquisas efetuadas, os documentos analisados e a exploração de ferramentas ao nível da geometria hiperbólica (técnicas, até então, desconhecidas por mim), proporcionou-me uma evolução grandiosa em termos tecnológicos. O conhecimento de factos históricos, de percursos efetuados por grandes matemáticos até à atualidade, provocou uma vontade enorme de exploração. (RD_P3)

Os formandos sentiram-se motivados para explorar diferentes formas de abordar conteúdos do programa da disciplina.

A tabela 5 apresenta resultados relativamente a formas de utilização da HM na aula de Matemática.

Tabela 5 Médias de concordância dos professores sobre formas de utilização da HM na aula de Matemática ( 𝑥 𝑖 , 𝑥 𝑓 ), coeficientes de variação ( 𝐶𝑉 𝑖 , 𝐶𝑉 𝑓 ), no início e final da formação, e valor-p. 

Das situações mais frequentes na utilização da HM, os professores realçaram, no início da formação, a introdução a um conteúdo matemático (100% níveis 3/4; média 3.7). Como menos frequente surge o uso da HM centrada na resolução de tarefas matemáticas (40% níveis 3/4; média 2.3). Todos os itens foram avaliados de forma francamente positiva (à exceção deste último, as médias variaram entre 2.6 e 3.7, sendo representativas).

Após a formação, os maiores destaques são na introdução a um conteúdo matemático, com menor pontuação e elevado decréscimo na média (1.3), e o aumento ao nível da utilização da HM centrada na resolução de tarefas matemáticas, com elevado acréscimo na média (0.6).

Pelo teste de Wilcoxon, nota-se uma evolução significativa nas respostas dos professores, em termos do reconhecimento das formas de utilização da HM, relativamente aos casos desenvolvimento de um conteúdo matemático e centrada na resolução de tarefas matemáticas (p=0.032 e p=0.041).

Estas alterações explicam-se pelo desafio lançado aos formandos de, em grupo, refletirem sobre diversas formas de integração da HM no ensino da disciplina e construírem tarefas matemáticas que envolvessem a HM para além da introdução a um conteúdo matemático. Os grupos criaram tarefas orientadas nos temas equações do 2.º grau, usando o método de Pedro Nunes (8.º ano) e método da falsa posição (simples e dupla), na resolução de problemas (9.º ano). Nas suas avaliações finais da formação, esclareceram ter sido sua preocupação abordar os conteúdos de forma diferente da usual levando os alunos a realizar uma aprendizagem ativa, daí perder-se a centralidade do papel do professor.

No questionário aplicado foi pedido aos professores que descrevessem uma das suas práticas de uso da HM na aula de Matemática.

Os exemplos apresentados antes da formação revelam uma forte ligação aos manuais escolares (por exemplo, história dos números complexos, Trigonometria, teorema de Pitágoras). Após a formação, a maior parte (75%) tem ligação direta à formação, por terem sido tópicos aí trabalhados, constituindo práticas distintas daquelas presentes em manuais escolares. Desses, destacamos a “Introdução à geometria”. Na formação foi trabalhado o aparecimento de outras geometrias, a partir do 5.º postulado de Euclides (postulado das paralelas). Os formandos aderiram muito bem a esta abordagem, com tarefas onde se conjugou o uso da HM com AGD e o telemóvel (este último, em tarefas envolvendo a “geometria do táxi”, com recurso a mapas para orientação na cidade de Braga). Evidência disso é a seguinte opinião: «nunca imaginei este tipo de problemas […] penso que vêm enriquecer a geometria e trazê-la da Grécia Antiga e das fórmulas de Descartes para a nossa rua» (P4).

A tabela 6 apresenta resultados sobre o impacto da utilização da HM nas aprendizagens dos alunos.

Tabela 6 Médias de concordância dos professores sobre impacto da utilização da HM nas aprendizagens Matemática ( 𝑥 𝑖 , 𝑥 𝑓 ), coeficientes de variação ( 𝐶𝑉 𝑖 , 𝐶𝑉 𝑓 ), no início e final da formação, e valor-p. 

Quanto ao reconhecimento do impacto do recurso à HM nas aprendizagens dos alunos, os professores, no início da formação, não divergem muitos na avaliação dos diversos itens, com resultados francamente positivos (níveis 3/4 entre 70% e 80%, médias entre 2.8 e 3.2 e representativas). O item mais bem pontuado foi o apreciar mais a Matemática (80% nos níveis 3/4 e média 3.2). Já o desenvolvimento de capacidades transversais foi o item menos bem pontuado (média 2.8, mas, ainda assim, com 70% nos níveis 3/4).

A avaliação global dos itens melhorou (nenhum avaliado com nível 1, níveis 3/4 superiores a 80% e médias entre 3.2 e 3.3), mantendo-se pouca divergência nas pontuações. As médias de pontuação aumentaram em todos os itens, sendo o maior aumento ao nível do desenvolvimento de capacidades transversais (0.5).

Pelo teste de Wilcoxon, nota-se uma evolução significativa nas respostas dos professores, em termos do reconhecimento do impacto do uso da HM nas aprendizagens dos alunos, ao nível do desenvolvimento de capacidades transversais, bem como na motivação (p=0.039 e p=0.047).

As mudanças que se verificaram na avaliação feita pelos professores decorrem das suas experiências de implementação de propostas recorrendo ao uso da HM, em regime a distância. Como exemplo disso, transcrevemos a posição de um dos professores:

Nas últimas aulas lecionadas on-line, tenho usado a História da matemática e efetivamente apercebi-me da importância que os alunos dão à história da evolução de determinado conteúdo, manifestando curiosidade e interesse no percurso desenvolvido até aos dias atuais. Questionam-me frequentemente, sobre o contexto real da aplicação destes saberes e qual o qual o contributo para o progresso e evolução da ciência. (RD_P4)

Na avaliação global da sua experiência de uso da HM na prática letiva, 90% dos professores consideram-na, antes da formação, positiva, aumentando a percentagem para 100%, após a formação.