Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Similares em
SciELO
Similares em
SciELO
Compartilhar
Psicologia
versão impressa ISSN 0874-2049
Psicologia vol.25 no.2 Lisboa dez. 2011
Avaliação da escala de auto-estima de Rosenberg mediante o modelo de rasch
Evaluation of Rosenberg self-esteem scale using rasch model
Sónia Quintãoa, Ana R. Delgadob e Gerardo Prietob
aFaculdade de Ciências Médicas da Universidade Nova de Lisboa (Portugal); CEDOC.
bUniversidad de Salamanca (Espanha)
RESUMO
O objectivo deste estudo consistiu em avaliar as características psicométricas da versão portuguesa da escala de Rosenberg mediante o modelo de Escalas de Classificação, uma extensão para itens politómicos do modelo de Rasch. Foi recolhida uma amostra de 510 estudantes universitários, 223 do sexo masculino e 287 do sexo feminino, com uma média etária de 21.7 anos (DP = 3.80). As análises indicam que o ajuste dos dados ao modelo é aceitável. Conclui-se que tanto o formato de resposta da versão portuguesa (tipo Likert com quatro categorias) como a fiabilidade dos dados resultam adequados. No entanto, de um ponto de vista substantivo e, em concordância com estudos prévios, constata-se que a escala não permite distinguir as pessoas com níveis médio e alto de auto-estima.
Palavras-chave: Auto-estima; Modelo de Rasch; Rosenberg; Portugal.
ABSTRACT
The objective of this study consisted on evaluating the psychometrical characteristics of the Portuguese version of the Rosenberg Scale by means of the Rating Scale model, an extension for the polytomic items of the Rasch Model. A sample of 510 college students was collected, 223 males and 287 females, with an average of 21.7 years (SD = 3.80). The analysis indicates that the adjustment of the data to the model is acceptable. We conclude that the response format from the Portuguese version (Likert type with four categories) as well as the reliability of the data, results adequate. However, from a substantive point of view, and in agreement with previous studies, it appears that the scale does not distinguish people with medium and high levels of self-esteem.
Key-words: Self-esteem; Rasch model; Rosenberg; Portugal
Avaliação da Escala de Auto-Estima de Rosenberg mediante o Modelo de Rasch
Rosenberg (1965) define auto-estima como uma avaliação que o indivíduo faz sobre si mesmo, que se expressa numa atitude positiva ou negativa em função de si, em que este aprova ou não o resultado. Uma auto-estima elevada implica que o indivíduo sinta que tem valor e inclui a dimensão dos sentimentos positivos que tem sobre si. Neste contexto, uma baixa auto-estima é originada por uma diminuição do indivíduo perante si próprio, através de uma auto-avaliação negativa. De acordo com este autor, a auto-estima global é baseada não só na avaliação da qualidade dos seus constituintes, como o auto-conceito, mas concomitantemente na avaliação das qualidades que são importantes para o indivíduo.
A escala de auto-estima de Rosenberg (1965) é a medida de auto-estima mais comummente utilizada em investigação (Ghaderi, 2005; Kwan, John, Kenny, Bond, & Robins, 2004) e está traduzida e validada para Portugal (Santos & Maia, 2003). A brevidade de aplicação, a linguagem acessível dos itens e os resultados positivos evidenciados no estudo original de validação, permitiram que esta escala se transformasse no padrão de referência na avaliação da auto-estima (Santos & Maia, 2003), embora exista um estudo (Gray-Little, Williams & Hancock, 1997) em que se sugeria que a escala de Rosenberg só é adequada para medir com precisão pessoas situadas nos níveis baixos do constructo de auto-estima.
A Teoria Clássica dos Testes (TCT) foi o principal modelo psicométrico empregue na construção e análise de testes. No entanto, foram assinaladas várias limitações à TCT, como utilizar distintas escalas para medir os sujeitos e os itens (o que impede a análise das suas interacções para construir interpretações sobre a variável medida), pressupor falsamente que o erro de medida é invariante ao longo da variável, etc. (Embretson, 1996). As suas limitações levaram a uma proposta de modelos alternativos, dos quais o mais harmonioso é o modelo de Rasch, que permite a medição conjunta de pessoas e itens numa mesma dimensão ou constructo (Prieto & Delgado, 2003; Stone, 2003). Assim, é um dos principais modelos que proporciona a objectividade específica para a construção de escalas, permitindo a independência das estimações com respeito à distribuição do atributo pelas pessoas em que é medido (Bond & Fox, 2001). Este modelo tem recebido muita atenção como revelam as publicações em distintas línguas, especificamente na língua portuguesa (Ziviani & Primi, 2002).
O modelo de Rasch, proposto por Georg Rasch (1960), fundamenta-se em dois pressupostos principais: o atributo que se pretende medir pode representar-se numa dimensão onde só se situariam conjuntamente as pessoas e os itens; o nível da auto-estima do inquirido e a dificuldade do item são os únicos determinantes da probabilidade de uma determinada resposta. Se o controlo da situação é adequado, esta expectativa é razoável e pode ser representada matematicamente através do modelo.
Rasch apresenta uma fórmula para modelar esta relação em itens dicotómicos: ln (Pis / 1 – Pis ) = (Bs – Di). Esta equação indica que o quociente entre a probabilidade de uma determinada resposta (por exemplo, concordo) e a probabilidade da outra resposta possível (discordo) num item (Pis / 1 – Pis), é função da diferença no atributo entre o nível da pessoa (Bs) e o nível do item (Di). Assim, quando uma pessoa responde a um item equivalente ao seu nível no atributo, terá a mesma probabilidade de uma resposta de concordar ou discordar (Pis / 1 – Pis = 0.50/0.50). Neste caso, o logaritmo natural de (Pis / 1 – Pis), reflecte que a dificuldade do item é equivalente ao nível do sujeito no atributo medido (Bs – Di=0) (Bond & Fox, 2001; Prieto & Delgado, 2003; Stone, 2003).
Existem extensões do modelo de Rasch para itens politómicos. Uma das formas de apresentar este tipo de dados, mais utilizadas na avaliação em saúde mental, são as escalas tipo Likert. O modelo estabelece a localização de cada ponto do item desde os itens mais baixos até os mais altos. Assim, cada item tem uma localização estimada. O modelo também estima os valores das categorias da escala para dar uma estrutura de qualificação à escala, que é partilhada por todos os itens que a compõem. Com dados dicotómicos, cada item tem uma estimação de localização e um erro de estimação associado. Com dados politómicos, não só cada item tem uma localização estimada como adicionalmente a escala tem uma série de pontos de transição (incremento na probabilidade de escolha de uma categoria de resposta em função do nível da auto-estima do inquirido) entre as categorias sucessivas. Podemos apresentar una extensão do modelo básico de Rasch para escalas com categorias ordenadas segundo o Modelo de Escalas de Classificação
(Rating Scale Model, Andrich, 1978): ln (Pnik / Pni(k-1)) = Bn – Di – Fk. Onde: Pnik é a probabilidade de que a pessoa n, perante o item i seja observada, ou responda, na categoria k; Pni(k-1) é a probabilidade de que a observação ou a resposta esteja na categoria k-1 ; Bn é a habilidade, atitude, etc., da pessoa n; Di é a dificuldade do item i; Fk é o ponto de transição entre a categoria k e a categoria k-1, i.e. o késimo passo de calibração, de onde as categorias se numeram 0, m.
Com base no exposto, foi objectivo do presente estudo a análise das características psicométricas da tradução portuguesa da escala de Auto-Estima de Rosenberg mediante o Modelo de Escalas de Classificação (MEC, Wright & Masters, 1982). Era esperado que a escala apresentasse características razoáveis ao nível da consistência interna, mas que não permitisse distinguir níveis médios e altos de auto-estima, tal como sugerido por Gray-Little, Williams e Hancock (1997) que referiram que a escala de Rosenberg só é adequada para medir com precisão pessoas situadas nos níveis baixos do constructo de auto-estima, devido aos itens serem muito orientados para os extremos do constructo.
Método
Participantes
Participaram no estudo 510 estudantes universitários, 223 do sexo masculino e 287 do sexo feminino, com uma média etária de 21.7 anos (DP = 3.80). A maior parte dos participantes eram solteiros (95.24%), estudantes do primeiro e segundo ano da universidade (52.39%), futuros licenciados em Letras, Direito e Historia (35.97%) e em Economia, Gestão, Contabilidade e Marketing (29.25%), sem profissão (90.34%).
Medidas
Rosenberg Self-esteem Scale (RSES; Rosenberg, 1965) é uma medidade auto-avaliação da auto-estima global. A RSES foi originalmente construída como uma escala de tipo Guttman embora, na maioria dos casos, os investigadores optem por um formato tipo Likert (Santos & Maia, 2003). A RSES original apresentava boas propriedades psicométricas: a sua consistência interna era elevada, com um valor de α de Cronbach igual a .92 (Rosenberg, 1965).
Um estudo internacional sobre as características psicométricas da escala, em 53 países, mostrou que a escala apresenta uma consistência interna pelo menos adequada em 50 desses países (α de Cronbach superior a .70), sendo o valor mais elevado de .90, com excepção da República Democrática do Congo, Etiópia e Tanzânia (Schmitt & Allik, 2005).
Este questionário, na versão portuguesa, é constituído por 10 itens, com um formato de resposta tipo Likert de quatro pontos (1. Concordo fortemente; 4. Discordo fortemente), 5 de orientação positiva e 5 de orientação negativa. A medida permite um resultado total, que varia de 10 a 40, crescendo em função do nível de auto-estima.
A escala traduzida apresenta, de uma forma genérica, qualidades psicométricas comparáveis às relatadas originalmente por Rosenberg (1965) e a outras versões de outras línguas (Schmitt & Allik, 2005; Shapurian, Hojat, & Nayerahmadi, 1987). Apresenta uma consistência interna adequada, com um valor de α de Cronbach igual a .86, e boa estabilidade temporal, dado que com um intervalo de duas semanas entre avaliações, o coeficiente de correlação de Pearson era igual a .90 (Santos & Maia, 2003).
Procedimento
A aplicação do questionário foi realizada em universidades (bibliotecas e salas de estudo). Pediu-se a colaboração desinteressada dos participantes de forma oral e por escrito, com informação prévia do objectivo do estudo e do tipo de participação pretendida, da confidencialidade e anonimato, da possibilidade de desistência durante a elaboração da avaliação, assim como da inexistência de respostas correctas ou incorrectas.
A recolha da amostra decorreu em diversas universidades da cidade de Lisboa, tendo a aplicação da prova demorado em média cinco minutos.
Codificação e análise dos dados
Uma vez recolhidos os dados, estes foram recodificados de maneira a que as categorias correspondentes aos itens que mediam em sentido inverso passarem a estar no sentido da variável medida, isto é, a maior valor corresponder maior auto-estima.
Os dados foram analisados com o programa Winsteps (Linacre & Wright, 2000).
Em primeiro lugar, realizou-se uma análise da funcionalidade das categorias de resposta, de acordo com os seguintes critérios estatísticos convencionais propostos por Linacre (2002, 2010):
1. Frequência suficiente e distribuição regular das categorias: as frequências baixas não são úteis para estimar as calibrações dos passos (Fk). O primeiro critério exige um mínimo de 10 observações dentro de cada categoria da escala. Baixas contagens dentro de uma categoria pode levar a estimativas imprecisas ou instabilidade nas calibrações dos passos. A situação ideal é uma distribuição uniforme, mas também é adequada uma distribuição unimodal ou bimodal com as frequências maiores nas categorias dos extremos.
2. As categorias não devem apresentar um desajuste elevado com o modelo.
Para pôr à prova o ajuste das pessoas, itens e categorias, usaram-se as médias dos resíduos (diferenças entre as respostas dadas e as esperadas) Outfit (média dos resíduos estandardizados elevados ao quadrado) e Infit (média dos resíduos estandardizados elevados ao quadrado, ponderados com a função de informação) que são as estatísticas que indicam o grau de ajuste. Outfit é muito sensível aos padrões de resposta inesperados (outliers), quetêm menos influência no Infit (Wright & Mok, 2004). O valor esperado para as duas estatísticas é a unidade (Wright, 1996). Valores altos indicam padrões anormais com respeito ao modelo, significando que há maior probabilidade de erro do que a probabilidade sistemática no item e valores baixos indicam possibilidade de existirem padrões aproximados aos modelos deterministas de resposta como o de Guttman (significando que pode existir probabilidade sistemática nas respostas ao item que não é explicada pela variável latente de interesse, que no presente estudo é a auto-estima). Os valores de Infit ou Outfit, superiores a 1.5 e inferiores a 2, indicam que o desajuste dos dados empíricos é moderadamente alto, mas não enfraquecem gravemente as medidas. No entanto, os valores superiores a 2 revelam um alto desajuste, assim como valores inferiores a .50 indicam possibilidade de existirem padrões aproximados aos modelos deterministas de resposta (Linacre, 2010).
3. Os pontos de transição (passos) entre as categorias sucessivas (Fk) devem aumentar monotonicamente (com ordenação crescente) o que significa que todas as categorias de resposta são funcionais, uma vez que cada categoria é a mais provável em algum ponto da variável.
No MEC, a probabilidade de seleccionar uma categoria depende do nível de auto-estima da pessoa. É desejável que exista algum intervalo no contínuo no qual cada categoria seja a mais provável de ser seleccionada (Linacre, 2002). Se isto suceder, os pontos de transição (Fk) estão ordenados monotonicamente. Quer dizer, F1<F2<F3, etc. Isto significa que no caso de quatro categorias tipo Likert, que as pessoas com um valor superior a F3 terão uma probabilidade superior de responder à categoria 4.
O funcionamento diferencial dos itens (FDI) é uma evidência da falta de validade das medidas. Produz-se quando existem factores alheios ao constructo, que se pretende medir, que afectam ilegitimamente as respostas. Em presença de FDI pode suceder que sujeitos com o mesmo nível no constructo, mas pertencentes a diferentes grupos sociodemográficos (por exemplo, homens e mulheres), tenham uma probabilidade distinta de uma resposta (Draba, 1977). De acordo com os pressupostos dos modelos tipo Rasch, a probabilidade da resposta a um item só dependerá do parâmetro da pessoa no atributo latente. Isto implica, por exemplo, que a probabilidade de 0.50 de estar de acordo com um item corresponde a um valor na variável que há-de ser a mesma para as pessoas de distintos grupos sociais. Ao contrário, a probabilidade da resposta está determinada por factores alheios ao constructo medido. Em consequência, as medidas obtidas com os itens careceriam da validade requerida.
Actualmente a análise de FDI é um passo obrigatório nos programas de validação de um teste (AERA, APA, NCME, 1999). Em consequência, levou-se a cabo uma análise do funcionamento diferencial dos itens da RSES, relacionada com o sexo, uma vez que a literatura aponta para a existência de diferenças entre sexos, apresentando os homens maior auto-estima (Hendricks, et al., 2001; Saigal, Lambert, Russ, & Hoult, 2002; Santos & Maia, 2003).
O procedimento implementado em Winsteps consiste em estimar em cada item a diferença entre o parâmetro de dificuldade em cada grupo e na amostra total. O contraste leva-se a cabo mediante a fórmula proposta por Wrigt e Panchapakesan (1969): t = Bf – Br / (SE2f + SE2r)1/2. Onde Bf – Br são os parâmetros de localização ajustados por sexo, e SE2f e SE2r são os seus SE (erros padrão) ao quadrado.
Um valor absoluto superior a 2 da estatística de contraste pode-se considerar uma evidência de FDI estatisticamente significativa. No entanto, segundo Wright e Douglas (1975), os valores de FDI que enfraquecem as medidas correspondem a diferenças (Bf – Br) superiores a 0.5 logit.
Resultados
Em primeiro lugar, foi analisada a qualidade psicométrica das categorias de resposta, de acordo com os critérios de Linacre (2002). Tal como se pode observar na Tabela 1, o sistema de quatro categorias, analisado com o Rating Scale Model, é adequado.
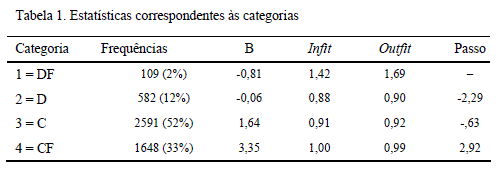
Pode observar-se que as categorias cumprem os critérios propostos por Linacre (2010): as frequências e a sua distribuição são adequadas, não há um desajuste elevado em nenhuma categoria (Outfit< 2) e os passos (step) entre as categorias sucessivas estão ordenados de forma crescente, ver Tabela 1.
Uma vez comprovada a adequação das categorias, foi analisado o ajuste dos itens e das pessoas, foram estimados os seus parâmetros e avaliada a sua fiabilidade. Na Tabela 2 são apresentadas as estatísticas de ajuste (Infit e Outfit), a localização (Di) e o erro padrão de medida dos itens (SE), ver Tabela 2.

Pode-se observar que não existem itens com valores de infit e/ou outfit superiores a 1.5 o que revela que os itens não se desajustam de forma severa (Linacre & Wright, 2000).
Na coluna Di, referente à dificuldade ou localização dos itens, podemos ver que o item 8 é o indicador de maior nível de auto-estima e o item 9 é o de menor nível.
Os erros padrão da medida dos itens oscilam entre .08 a .10, o que indica que a fiabilidade dos itens é elevada. A fiabilidade global das estimações dos itens pode ser avaliada mediante a estatística denominada Item Separation Reliability que indica a proporção da variância observada dos itens não explicada pelo erro de medida (Smith & Smith, 2004). Como se pode observar na Tabela 3 a fiabilidade dos itens é muito alta (.99), ver Tabela 3.
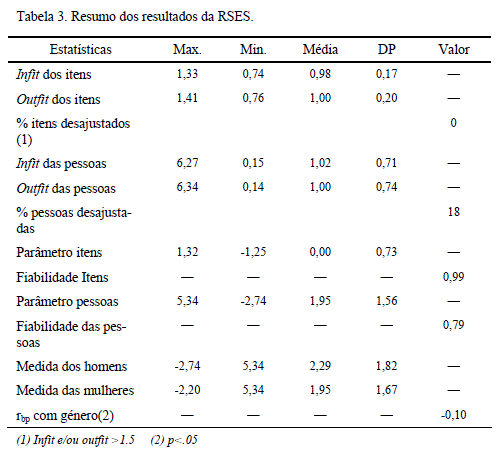
O ajuste das pessoas ao modelo não é razoável, pois apesar de o valor da média e do desvio-padrão serem 1.02 e .71 (infit), e 1.00 e .74 (outfit), o número de pessoas com infit e/ou outfit superior a 1.5 é elevado: 87 (18%). Inferior a .5 estão 107 sujeitos (22%), o que pode dever-se à existência de vários itens similares ou muito correlacionados que inflacionam as fiabilidades.
Os parâmetros das pessoas vão de 5.34 a-2.74 com uma média de 1.95 e desvio-padrão de 1.56. A fiabilidade global das pessoas (.79) não é excelente, embora razoável (percentagem da variância das pessoas não explicada pelo erro). Este valor é similar ao α de Cronbach da teoria clássica.
A correlação entre sexo e a medida dos itens, embora seja significativa (p = .03 < .05) é muito reduzida (r = -.10). Não aparece nenhuma outra correlação significativa com outras variáveis demográficas.
A Tabela 4 mostra uma representação conjunta pessoa-item, onde se pode observar a posição dos itens e das pessoas na variável. Este tipo de representação facilita a comunicação dos resultados e das suas implicações. A coluna da Escala representa os valores estimados da variável latente auto-estima, sendo que quanto maior forem estes valores, maior é o nível de auto-estima. Dado que a média das pessoas (1.95) é muito superior à dos itens, pode-se considerar que o nível de auto-estima dos sujeitos analisados é muito alto. Além do mais, a maior parte das pessoas encontram-se acima do ponto da variável em que os itens se situam. Em consequência, porque a média dos itens é alta (i.e., dificuldade baixa) o que corresponde a indivíduos com valores de logit baixos (i.e., baixos valores na variável latente) tenderem a concordar fortemente com os itens da escala), observa-se que os itens da escala não permitem medir com elevada precisão as pessoas com níveis médio e alto de auto-estima, ver Tabela 4.

Na Tabela 5 apresentam-se os resultados da análise de Funcionamento Diferencial dos Itens associado ao sexo, ver Tabela 5.
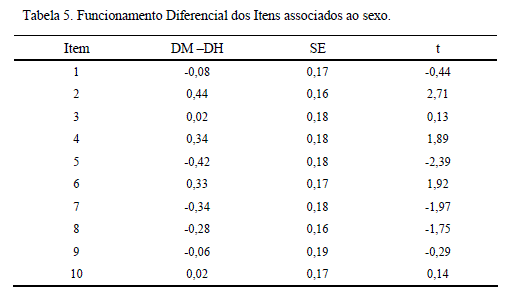
De acordo com a distribuição normal, t≥|2| indica DIF. Neste caso, só os itens 2 e 5 mostram DIF, mas os valores não são muito altos, não enfraquecem a medida, pois não têm diferenças superiores a 0.5 logit. O item 2 indica um maior nível de auto-estima nas mulheres (di2=.44) e o item 5 nos homens (di5=-.42).
Discussão
O objectivo deste estudo foi realizar uma análise das características psicométricas da escala de auto-estima de Rosenberg (RSES) numa amostra de alunos universitários portugueses. Os dados foram analisados mediante o modelo de Escalas de Classificação (Wright & Masters, 1982), uma extensão para itens politómicos do modelo de Rasch.
Neste estudo pretendia-se determinar o melhor sistema de categorias de resposta. Os resultados mostraram que o sistema original de quatro categorias tem boa qualidade psicométrica.
Com relação aos itens da RSES, a fiabilidade é muito alta. O ajuste das pessoas ao modelo está no limite do razoável. A fiabilidade global das pessoas não é excelente, embora resulte adequada. Sendo este valor similar ao α de Cronbach da teoria clássica, pode-se assim afirmar que está de acordo com os resultados da fiabilidade clássica da RSES apresentados por outros autores (Schmitt & Allik, 2005), ainda que mais reduzido do que aparece em outros estudos (Rosenberg, 1965; Santos & Maia, 2003; Shapurian, Hojat, & Nayerahmadi, 1987; Schmitt & Allik, 2005).
Alguns estudos prévios com a escala original colocaram a possibilidade de que a escala não permitisse distinguir as pessoas com nível médio das pessoas com nível elevado de auto-estima (Gray-Little, Williams & Hancock, 1997). Os resultados indicam que a média das pessoas é superior à dos itens, o que revela que a maior parte das pessoas se encontra num nível superior ao do nível da variável em que os itens se situam, ou seja com mais auto-estima. Em consequência, observa-se que os itens da escala não permitem medir com alta precisão as pessoas com níveis médio e alto de auto-estima. Isto sucede porque a escala só tem itens adequados para o leque inferior do constructo. Este resultado está de acordo com o afirmado no estudo de Gray-Little et al. (1997) que sugeriam que a escala de Rosenberg só é adequada para medir com precisão pessoas situadas nos níveis baixos do constructo de auto-estima.
Só os itens 2 e 5 mostram FDI, mas os valores não são muito altos, não enfraquecem a medida, logo a comparação entre homens e mulheres resulta adequada. O item 2 indica um maior nível de auto-estima nas mulheres e o item 5 nos homens. Tanto no item 2 (Por vezes penso que não sou bom em nada) como no item 5 (Sinto que não tenho muito de que me orgulhar), não é fácil encontrar uma explicação clara para as diferenças de resposta entre sexos. Podemos assim concluir que a medida pode ser utilizada igualmente nos dois géneros.
Tal como se esperava, os homens apresentaram um valor médio de auto-estima mais elevado que as mulheres, embora o tamanho do efeito seja baixo, seguindo critérios convencionais (Cohen, 1998) . Este dado está de acordo com o publicado por outros autores (Hendricks, et al., 2001; Saigal, Lambert, Russ, & Hoult, 2002; Santos & Maia, 2003; Turner, Pickering, & Johnson, 1998) . Não foram encontradas correlações significativas com outras variáveis demográficas, o que pode dever-se ao facto de a população universitária ser uma população com características muito mais homogéneas que as da população geral.
Finalmente, tal como se havia discutido em estudos anteriores, os dados recolhidos com a escala de auto-estima de Rosenberg mostraram uma boa fiabilidade.
Em conclusão, os aspetos mais positivos da escala são que as categorias funcionam adequadamente, a fiabilidade média dos sujeitos é aceitável e a fiabilidade dos itens é elevada.
Por outro lado, confirma-se que os itens da escala não permitem medir com elevada precisão as pessoas com níveis médio e elevado de auto-estima. Isto acontece porque o nível das pessoas é elevado e a escala só tem itens para auto-estima reduzida. Este é o aspeto mais criticável da escala RSES. Estes resultados podem estar de qualquer forma algo mascarados pelo efeito da desejabilidade social, embora se tenha passado o questionário de forma anónima e pelo facto de que os participantes serem estudantes universitários, não sendo portanto representativos da população geral. Esta poderia ser também a justificação para que as diferenças sexuais em auto-estima tenham resultado menores de que o defendido em estudos prévios.
Uma limitação deste estudo prende-se por a amostra só ter sido recolhida em Lisboa, não sendo representativa da população universitária portuguesa.
Em qualquer caso, parece necessário construir uma nova escala de auto-estima que permita avaliar adequadamente um leque mais amplo do constructo.
Referências
AERA, APA, NCME (1999). The standards for educational and psychological testing. Washington, DC: AERA. [ Links ]
Andrich, D. A. (1978). A rating formulation for ordered response categories. Psychometrika, 43, 561-573. [ Links ]
Bond, T. G., & Fox, C. M. (2001). Applying the Rasch Model. Mahwah, NJ: LEA. [ Links ]
Cohen, J. (1998). Statistical power analysis for the behavioral sciences (2nd ed.). Hillsdale, NJ: LEA. [ Links ]
Draba, R. E. (1977). The identification and interpretation of item bias. [ Links ]
Embretson, S. E. (1996). The new rules of measurement. Psychological Assessment, 4, 341-349. [ Links ]
Ghaderi, A. (2005). Psychometric properties of the self-concept questionnaire. European Journal of Psychological Assessment, 21, 139-146. [ Links ]
Gray-Little, B., Williams, V.S.L., & Hancock, T.D. (1997). An item response theory analysis of the Rosenberg Self-Esteem Scale. Personality and Social Psychology Bulletin, 23, 443-451. [ Links ]
Hendricks, C. S., Tavakoli, A., Hendricks, D. L., Harter, N. R., Campbell, K. P., LEcuver, R. I., Geddings, A. A., Hackett, D., & Mathis, D. (2001). Self-esteem matters: Racial & gender differences among rural southern adolescents. Journal of Nacional Black Nurses Association, 12, 15-22. [ Links ]
Kwan, V. S. Y., John, O. P., Kenny, D., Bond, M. H., & Robins, R. W. (2004). Reconceptualizing individual differences in self-enhancement bias: An interpersonal approach. Psychological Review, 111, 94-110. [ Links ]
Linacre, J. M. (2002). Optimizing rating scale category effectiveness. Journal of Applied Measurement, 3, 85-106. [ Links ]
Linacre, J. M. (2010). A users guide to winsteps ministep. Rasch-model computer programs. Retirado em 5, Abril, 2010, de www.winsteps.com. [ Links ]
Linacre, J. M., & Wright, B. D. (2000). WINSTEPS: Multiple-choice, rating scale, and partial credit Rasch análisis (Computer software). Chicago: MESA Press. [ Links ]
Prieto, G., & Delgado, A. R. (2003). Análisis de un test mediante el modelo de Rasch. Psicothema, 15, 94-100. [ Links ]
Rasch, G. (1960). Probabilistic Models for some intelligence and attainment tests. Copehagen: Institute for Educational Reseca. [ Links ]
Rosenberg, M. (1965). Society and the adolescent self-image. Princeton, NJ: Princeton University Press. [ Links ]
Saigal, S., Lambert, M., Russ, C., & Hoult, L. (2002). Self-esteem of adolescents who were born prematurely. Pediatrics, 109, 429-433. [ Links ]
Santos, P. J., & Maia, J. (2003). Análise factorial confirmatória e validação preliminar de uma versão portuguesa da escala de autoestima de Rosenberg. Psicología: Teoria, Investigação e Prática, 8, 253-268. [ Links ]
Schmitt, D. P., & Allik, J. (2005). Simultaneous administration of the rosenberg self-esteem scale in 53 nations: exploring the universal and culture-specific features of global self-esteem. Journal of Personality & Social Psychology, 89, 623-642. [ Links ]
Shapurian, R., Hojat, M., & Nayerahmadi, H. (1987). Psychometric characteristics and dimensionality of Pearsian versión of Rosenberg Self-Esteem Scale. Perceptual and Motor Skills, 65, 27-34. [ Links ]
Smith, E. V., & Smith, R. M. (Eds) (2004). Introduction to Rasch measurement. Maple Grove, Mn: JAM Press. [ Links ]
Stone, M. H. (2003). Substantive scale construction. Journal of Applied Measurement, 4, 282-297. [ Links ]
Turner, L. A., Pickering, S., & Johnson, R. B. (1998). The relationship of attributional beliefs to self-esteem. Adolescente, 33, 477-484. [ Links ]
Wright, B. D. (1996). Reasonable mean-square fit values. In Wright, B.D., & Linacre JM, (Eds.) Rasch measurement transactions. Part 2. Chicago: MESA Press. [ Links ]
Wright, B. D., & Douglas, G. A. (1975). A better procedures for sample-free item analysis. Research Memorandum. Statistical Laboratory. Department of Education. University of Chicago. [ Links ]
Wright, B. D., & Masters, G. N. (1982). Rating scale analysis. Chicago: MESA Press. [ Links ]
Wright, B. D., & Mok, M. M. C. (2004). An overview of the family of Rasch measurement models. In Smith, E. V., & Smith, R. M. (Eds.) Introduction to Rasch Measurement. Maple Grove: JAM Press. [ Links ]
Wright, B. D., & Panchapakesan, N. (1969). A procedure for simple-free item análisis. Educational and Psychological Measurement, 29, 23-48. [ Links ]
Ziviani, C., & Primi, R. (2002). Teoria da resposta ao item o modelo Rasch de mensuraçao: Uma análise de provas de psicologia. In R. Primi (Org.). Temas em Avaliaçao Psicológica (pp. 131-151). Campinas: IBAP. [ Links ]













