Precisão das equações preditivas de 1-RM em praticantes não competitivos de treino de força

 

M.L. Lacio ¹, V.O. Damasceno ², J.M. Vianna ³, J.R.P. Lima ³, V.M. Reis ⁴, J.P. Brito ⁵, J. Fernandes Filho ⁶

¹ Universidade Castelo Branco, Rio de Janeiro, Brasil.

² Escola de Educação Física e Desporto – Universidade Federal de Juiz de Fora, Juiz de Fora, Brasil; Universidade Salgado de Oliveira – Campus Juiz de Fora, Brasil.

³ Escola de Educação Física e Desporto – Universidade Federal de Juiz de Fora, Juiz de Fora, Brasil.

⁴ Universidade de Trás-os-Montes e Alto Douro, Vila Real, Portugal; Centro de Investigação em Desporto, Saúde e Desenvolvimento Humano, Vila Real, Portugal.

⁵ Escola Superior de Desporto de Rio Maior, Instituto Politécnico de Santarém, Portugal; Centro de Investigação em Desporto, Saúde e Desenvolvimento Humano, Vila Real, Portugal.

⁶ Universidade Federal do Rio de Janeiro, Rio de Janeiro, Brasil.

Endereço para correspondência

 

RESUMO

O objetivo deste trabalho foi determinar a precisão das equações de predição de 1-RM propostas por Adams (1994), Baechle e Groves (2000), Brzycki (1993), Epley (1985), Lander (1985) e O’Conner et al. (1989) em alunos de ginásios. Foram selecionados 31 indivíduos do sexo masculino, praticantes de treino de força, com média de idades de 21.8 ± 4.0 anos, peso 75.9 ± 8.4 kg e estatura 178.1 ± 6.4 cm. O exercício escolhido para a realização do presente estudo foi o supino recto com barra. A coleta de dados referentes às cargas de trabalho no supino recto foi realizada em dois momentos: (a) carga referente ao teste de 1-RM; e, (b) carga referente ao teste submáximo e seus respectivos números de repetições. Através da análise de variância verificou-se que não houve diferença significativa (p > .05) entre os resultados das equações e o teste de 1-RM. Os coeficientes de determinação (r²) variaram entre .94 e .96. As equações tiveram erro padrão baixo (2.7 a 3.2 kg). Podemos concluir, com este trabalho, que as equações para predição de carga máxima selecionadas podem ser utilizadas com o intuito de predizer a carga máxima para o supino recto com barra com alto grau de precisão em alunos de academia.

Palavras-chave: treino de força, predição da 1-RM, precisão das equações

 

Precision of 1-RM prediction equations in non-competitive subjects performing strength training

ABSTRACT

The purpose of this study was to assess the precision of the 1-RM prediction equations proposed by Adams (1994), Baechle and Groves (2000), Brzycki (1993), Epley (1985), Lander (1985) and O’Conner et al. (1989) for strength assessment in fitness programs. Thirty one healthy regular strength training male practitioners (mean ± SD: 21.8 ± 4.0 years of age; 75.9 ± 8.4 kg of weight; and 178.1 ± 6.4 cm of height) performed two tests on the bench press exercise: (a) maximum test - determination of the 1-RM load; and (b) submaximum test - determination of the load matching 4 to 10 maximum repetitions. Analysis of variance (ANOVA) found no significant difference (p > .05) between maximum load determination through prediction equations or through the 1-RM test. The coefficient of determination (r²) varied from .94 to .96. The prediction equations had small standard error of estimate (2.7 to 3.2 kg). Results indicate that the 1-RM prediction equations could be used to determine the maximum load at the bench press exercise in subjects with low strength training experience.

Keywords: strength training, 1-RM prediction, equations precision

 

 

O treino de força (TF) é uma das formas de exercício mais utilizadas para o condicionamento físico, tanto de atletas, quanto de não atletas (Fleck & Kraemer, 1999). A popularidade crescente do treino de força tem estimulado investigação sobre os seus efeitos (Baechle & Groves, 2000). São vários os autores (Myer, Ford, Palumbo, & Hewett, 2005; Manso, 1999; O’Conner, Simmons, & O’Shea, 1989) que relatam efeitos do treino de força na melhoria da performance desportiva e do estado de saúde dos indivíduos, nomeadamente, melhoria da composição corporal, prevenção de problemas posturais, articulares e lesões músculo-esqueléticas.

O American College of Sports Medicine (ACSM, 2002), cita a importância do TF para a manutenção da qualidade de vida das pessoas e recomenda que sejam realizados de 2 a 3 sessões por semana, de 8 a 10 exercícios para os principais grupos musculares por sessão e, de 8 a 15 repetições por exercício. Para que um programa de TF produza os efeitos desejados, é muito importante que as cargas de treino sejam criteriosamente determinadas. Somente através da utilização da carga correta é que um programa de exercícios de força poderá atingir o sucesso com atletas (Fleck & Kraemer, 1999).

Existem diferentes formas para prescrever a carga de treino. A forma mais popular e simples para determinação da carga de trabalho é o teste da uma repetição máxima (1-RM) ou teste de carga máxima (Cosgrove & Mayhew, 1997; Manso, 1999), que é a máxima carga que pode ser levantada em apenas uma repetição completa (Pereira & Gomes, 2003). Após a identificação da 1-RM, as cargas de treino serão, então, prescritas de acordo com a percentagem da carga máxima (%1-RM) (Abadie & Wentworth, 2000) que objectiva as adaptações pretendidas. O quadro 1 mostra alguns exemplos sobre o valor das percentagens da carga máxima e respectivas adaptações inerentes ao processo de treino (Dantas, 2002).

 

Quadro 1

Relação entre adaptações provocadas pelo treino e a percentagem da 1-RM

 

O teste de 1-RM é frequentemente utilizado por treinadores, especialistas na área de reabilitação e profissionais do fitness e da saúde (Braith, Graves, Leggett, & Pollock, 1993). Porém, por se tratar de uma metodologia que utiliza cargas máximas, este método é contra-indicado para indivíduos iniciantes no TF, para crianças, adolescentes e adultos sedentários, idosos, hipertensos e cardíacos e nos casos de recuperação muscular (Abadie & Wentworth, 2000; Manso, 1999; Pereira & Gomes, 2003), pelo risco elevado de causar lesões musculo-esqueléticas (Mayhew, Ware & Prinster, 1993).

A sua utilização é também na maioria das vezes muito demorada. Devido a estas limitações impostas pelo teste de 1-RM, algumas equações foram desenvolvidas visando estimar a carga máxima que um indivíduo pode suportar através da utilização de cargas submáximas. Destes estudos surgiram, então, equações de regressão para predição da carga máxima através da utilização de cargas submáximas.

Muitos são os trabalhos sobre predição de cargas máximas através da utilização de cargas submáximas. Berger (citado por Abadie & Wentworth, 2000) e Carpinelli (2002), executou 1-RM, 5-RM e 10-RM no exercício supino plano. Através dos dados coletados, foram estimados valores de 1-RM utilizando valores obtidos com cargas que permitiam a realização de 2-RM a 10-RM, com alto grau de correlação (r = .96). Braith, Graves, Leggett e Pollock (1993) realizaram 7-RM a 10-RM no exercício de extensão de pernas (cadeira extensora), verificando um coeficiente de correlação de r = .94 com o teste de 1-RM. Existem muitos estudos relacionando a precisão de algumas equações de predição de 1-RM (Altorfer, Abadie & Schuler, 1997; Dohoney, Chromiak, Lemire, Abadie & Kovacs, 2002; Ploutz-Snyder & Giamis, 2001). A eficiência destas equações depende da sua fiabilidade de estimação da 1-RM (Mayhew, Prinster, Ware, Zimmer, Arabas, & Bemben, 1995). Apesar da grande quantidade de estudos, muitas equações, já com uso generalizado, não apresentam ainda indicadores da sua adequabilidade para praticantes habituais de treino da força em centros de fitness. Muitas destas equações apresentam semelhanças, apresentando em sua composição as mesmas variáveis e possuindo, assim, resultados muito próximos. Algumas das equações mais frequentemente utilizadas são expostas no quadro 2.

 

Quadro 2

Equações de predição de 1-RM

 

As equações de O’Conner et al. (1989) e Baechle e Groves (2000) são muito semelhantes: a carga máxima (1-RM) é o produto de uma constante (cujos valores são muito próximos) pelo número de repetições. Ao valor encontrado, adiciona-se o valor de outra constante. Para alcançar o resultado final multiplica-se o valor encontrado até então pela carga realizada no teste submáximo. A equação proposta por Epley (Epley, 1995) diferencia-se, pois o valor da carga é multiplicado por uma constante e o resultado é novamente multiplicado pelo número de repetições e adicionado à carga atingida no teste submáximo.

As equações de Brzycki (Brzycki, 1993) e Lander (Lander, 1985) apresentam valores de %1-RM similares. Das equações referidas no quadro 2, a equação de Adams (Adams, 1994) considera que para cada repetição realizada, a carga suportada cai em aproximadamente 2%. Assim, multiplicando-se 2% pelo número de repetições realizadas, encontra-se o percentual de queda em relação a 1-RM. Então, a carga utilizada para um determinado número de repetições corresponde ao valor percentual de perda em relação à carga máxima.

O objectivo deste estudo é investigar a precisão das equações de predição de 1-RM relacionadas no quadro 2, quando comparadas ao teste de 1-RM numa população de praticantes habituais de treino da força.

 

MÉTODO

Amostra

Trinta e um indivíduos do sexo masculino, aparentemente saudáveis (média ± DP: idade, 21.8 ± 4.0 anos; peso, 75.9 ± 8.4 kg; altura, 178.1 ± 6.4 cm), praticantes de treino de força numa base regular (3 - 4 sessões/semana) participaram no estudo. Todos os indivíduos foram informados sobre os procedimentos adoptados para a realização dos testes e assinaram a declaração de consentimento informado. O exercício escolhido para a realização do presente estudo foi o supino recto com barra, pelo facto de ser um exercício estrutural e poliarticular. Antes dos testes, os indivíduos receberam instruções padronizadas sobre a técnica de execução. Este estudo está de acordo com as normas da Declaração de Helsinque de 1975.

Instrumentos e Procedimentos

O exercício supino recto com barra foi realizado em um banco próprio (Body and Soul, Brasil), utilizando uma barra de 1.80 m e discos de .5 kg a 25 kg. A partir da posição de deitado em decúbito dorsal, com joelhos e quadris semiflexionados, com os pés sobre o apoio do próprio aparelho, dois ajudantes (certificados pelo National Strenght and Conditioning Association), colocavam a barra nas mãos do sujeito, que iniciava o teste com os braços em extensão. A distância entre as duas mãos na pega na barra era medida previamente de forma que, quando os braços assumissem a posição paralela ao solo, os cotovelos descrevessem um ângulo de 90^o. O movimento descendente (fase excêntrica), era executado em 2 segundos e até tocar levemente o peito do sujeito, no ponto meso-esternal. Nenhuma assistência física era dada para ajudar os participantes a completar a fase concêntrica da repetição. A repetição era válida quando os braços se encontravam em extensão.

A recolha de dados referentes às cargas de trabalho no supino recto foram divididas em 2 partes: 1^º) carga referente ao teste de 1-RM (carga máxima); e, 2^º) carga referente ao teste submáximo e respectivo número de repetições. O teste de 1-RM e o teste submáximo foram realizados em dias diferentes (entre 48 e 72 horas), de forma a evitar fadiga acumulada.

Protocolo do Teste de 1-RM

Antes de realizar o teste propriamente dito os sujeitos realizaram um de aquecimento, que segundo Kraemer e Fry (1995), consiste de 5 a 10 repetições, com uma carga equivalente a 40 a 60% da máxima percebida, seguido de alongamentos por um minuto. A seguir, a carga foi aumentada para uma carga de, aproximadamente, 60 a 80% da máxima percebida. Após este aquecimento, os indivíduos respeitaram um intervalo de 2 minutos, enquanto a carga era incrementada para a realização do teste. O movimento era realizado com o indivíduo podendo ou não vencer a resistência oferecida e após um intervalo de 5 minutos a carga era, respectivamente, aumentada ou diminuída para permitir a realização de uma única repetição (Dias, Cyrino, Salvador, Caldeira, Nakamura, & Papst, 2005). O número máximo de tentativas permitidas na mesma sessão foi de três, conforme procedimento descrito na literatura (Marins & Giannichi, 1996).

Protocolo do Teste submáximo

Após a realização do mesmo protocolo de aquecimento do teste de 1-RM, um carga de aproximadamente 80 a 100% da carga máxima percebida era selecionada. Aos sujeitos foi solicitado a realização do maior número de repetições, que no caso deste estudo ficaram entre 4 e 10 repetições máximas.

Análise estatística

Os dados foram analisados com o software SPSS 13.0 (SPSS Science, Chicago, USA). A análise exploratória dos dados incluiu medidas descritivas e confirmação do pressuposto de normalidade (teste de Kolmogorov-Smirnov). As diferenças entre medidas foram testadas pela ANOVA com post-hoc de Scheffé. As associações entre variáveis foram investigadas por regressões lineares simples. Os resultados são apresentados como médias e desvios padrão (M ± DP).

 

RESULTADOS

No teste de 1-RM a carga obtida foi de 76.23 ± 12.52 kg, com valores mínimos e máximos de, respectivamente, 58.0 e 100.0 kg. No teste submáximo, o número de médio de repetições foi de 7.29 ± 1.62 reps, com variação de 4 a 10 RM. A carga média utilizada no teste submáximo foi de 61.9 ± 12.16 kg, com variação de 46.0 a 86.0 kg.

Os valores de carga encontrados com a aplicação das equações preditivas da 1-RM variaram de 73.05 ± 13.75 kg a 77.38 ± 15.19 kg.

Os valores mínimos e máximos encontrados variaram de 50.19 a 107.50 kg (ver quadro 3).

 

Quadro 3

Valores estimados de 1-RM através da utilização das equações de regressão (n = 31)

 

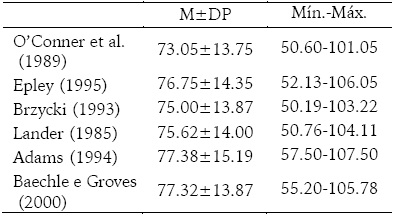
A análise de variância mostrou que não há diferenças significativas (p > .05) entre os resultados das equações. As equações preditivas da 1-RM tiveram um erro padrão baixo (EP), variando entre 2.7 e 3.2 kg. Os coeficientes de determinação (r²) variaram de .94 a .96, conforme mostra o quadro 4 e as figuras de 1 a 6.

 

Quadro 4

Correlação (r²) e erro padrão (EP) de estimativa das equações de regressão

 

 

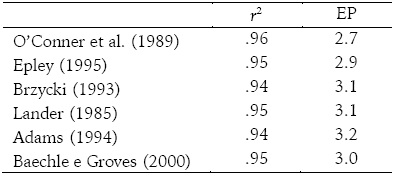
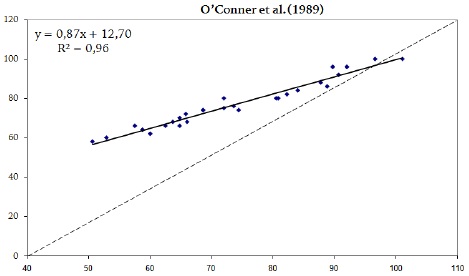
Figura 1. Correlação entre o resultado da equação de O’Conner et al. (1989) e o resultado de 1-RM

 

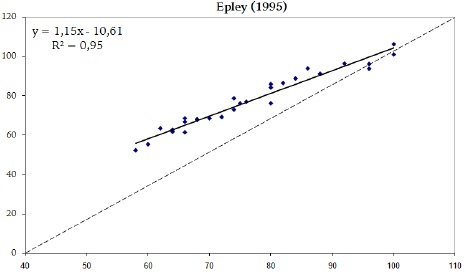
Figura 2. Correlação entre o resultado da equação de Epley (1995) e o resultado de 1-RM

 

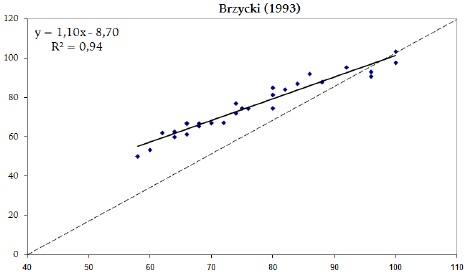
Figura 3. Correlação entre o resultado da equação de Brzycki (1993) e o resultado de 1-RM

 

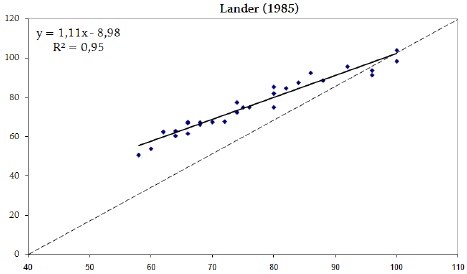
Figura 4: Correlação entre o resultado da equação de Lander (1985) e o resultado de 1-RM

 

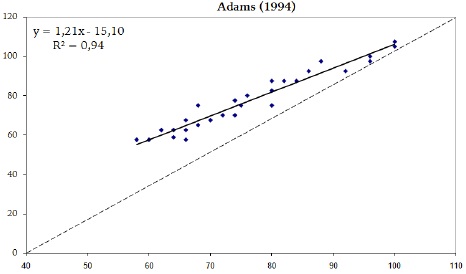
Figura 5. Correlação entre o resultado da equação de Adams (1994) e o resultado de 1-RM

 

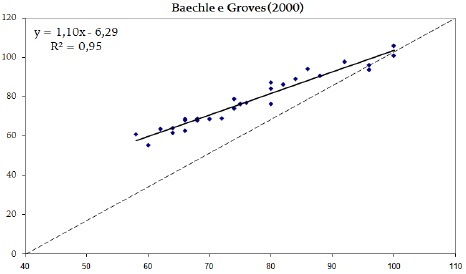
Figura 6. Correlação entre o resultado da equação de Baechle e Groves (2000) e o resultado de 1-RM

 

DISCUSSÃO

O teste de 1-RM é um método muito utilizado para a mensuração da carga máxima nos exercícios de musculação (Manso, 1999). Porém, apresenta algumas contra-indicações quanto a seu uso. De forma a melhorar o acesso à 1-RM, foram desenvolvidos modelos matemáticos para predição de carga máxima através da utilização de cargas submáximas. Tais equações apresentam, hoje, grande utilização entre os profissionais que trabalham nas salas de musculação. O objectivo deste trabalho foi estudar a precisão das equações aplicadas a uma amostra especifica de praticantes de treino da força em ginásios e academias.

Os resultados encontrados no estudo estão em concordância com alguns estudos de predição de 1-RM através da utilização de cargas submáximas realizados com outras populações. Os valores obtidos com a aplicação das equações preditivas apresentam valores de correlação elevados com os do teste de 1-RM. Berger (citado por Abadie & Wentworth, 2000) obteve uma correlação de .96 em sua predição de 1-RM realizando 2 a 10 repetições. Braith et al. (1993) obtiveram correlação de .94 na predição na cadeira extensora. Cummings e Finn (1998), numa investigação com 57 mulheres com idade de 18 a 50 anos, determinaram através de 4-8 RM, o valor de 1-RM para o supino recto com uma correlação de .94. Rose e Ball (1992) avaliaram mulheres de 18 a 25 anos e encontraram correlações de .78 a .82, utilizando cargas de 15.9 kg e 20.4 kg, respectivamente. Pereira e Gomes (2003), através de uma revisão crítica acerca do assunto, também encontraram forte relação entre equações preditivas e o teste de 1-RM. Os referidos autores recomendam que quando os testes forem utilizados em estudos, a fiabilidade das equações deve ser verificada antes do início do estudo.

Concluímos, então, que todas as equações utilizadas no estudo para a predição de carga máxima, podem ser empregues com o intuito de predizer, para o exercício supino recto com barra, o valor de 1-RM com alto grau de confiança, auxiliando, assim, os profissionais na avaliação e prescrição do treino de força. Porém, recomenda-se que sejam realizados outros estudos com outras populações (por exemplo: adolescentes, idosos e mulheres), outros grupos musculares, velocidades de execução, biótipos e tempos de treino diferentes para verificar a precisão de tais equações.

 

REFERÊNCIAS

Abadie, B. R., & Wentworth, M. C. (2000). Prediction of one repetition maximal strength from a 5-10 repetition submaximal strength test in college-aged females. Journal of Exercise Physiology - Online, 3,1-7

Adams, G. M. (1994). Exercise physiology: Laboratory manual (2^a ed.). Dubuque, Iowa: Brown & Benchmark Publishers.

Altorfer, G. L., Abadie, B. R., & Schuler, P. B. (1997). Does a regression equation to predict maximal strength in novice lifters, remain valid when the subjects are technique trained? Medicine & Science in Sports & Exercise, 28, S8.

American College of Sports Medicine (2002). ACSM Position Stand: Progression models in resistance training for healthy adults. Medicine & Science in Sports & Exercise, 34, 364-380.

Baechle, T. R., & Groves, B. R. (2000). Treino de força: Passos para o sucesso (2^a ed.). Porto Alegre: Artmed.

Braith, R. W., Graves, J. E., Leggett, S. H., & Pollock, M. L. (1993). Effect of training on the relationship between maximal and submaximal strength. Medicine & Science in Sports & Exercise, 25,132-138.

Brzycki, H. (1993). Strength testing: Predicting a one-rep max from reps-to-fatigue. Journal of Physical Education, Recreation & Dance, 64, 88-90.

Carpinelli, R. N. (2002). Berger in retrospect: Effect of varied weight training programmes on strength. British Journal of Sports Medicine, 36, 320-324.

Cosgrove, L., & Mayhew, J. (1997). A modified YMCA bench press test to predict strength in adult women. IAHPERD Journal, 30(2). Consultado em 12 de Junho de 2009 a partir de http://www.iowaahperd.org/journal/j97s_bench.html

Cummings, B., & Finn, K. J. (1998). Estimation of on repetition maximum bench press strength for untrained women.Journal of Strength Condition Research, 12, 262-265.

Dantas, E. H. M. (2002). A montagem e quantificação de uma série de musculação. Fitness & Performance Journal, 1(4), 135-142.

Dias, R. M. R., Cyrino, E. S., Salvador, E. P., Caldeira, L. F. S., Nakamura, F. Y., & Papst, R. R. (2005). Influência do processo de familiarização para avaliação da força muscular em testes de 1-RM. Revista Brasileira de Medicina do Esporte, 11(6), 319-324.

Dohoney, P., Chromiak, J. A., Lemire, D., Abadie, B. R., & Kovacs, C. (2002). Prediction of one repetition maximum (1-RM) strength from a 4-6 RM and a 7-10 RM submaximal strength test in healthy young adult males. Journal of Exercise Physiology - Online, 5, 54-59.

Epley, B. (1995). Poundage chart: Boyd Epley workout. Lincoln, NE: University of Nebraska.

Fleck, S. J., & Kraemer, W. J. (1999). Fundamentos do treino de força muscular (2^a ed.). Porto Alegre: Artmed.

Kraemer, W. J., & Fry, A. C. (1995). Strength testing: Development and evaluation of methodology. In P. J. Maud, & C. Foster (Eds.), Physiological assessment of human fitness (pp. 115-138). Champaign, IL: Human Kinetics.

Lander, J. (1985). Maximum based on reps. National Strength Conditioning Association Journal, 6, 60-61.

Manso, J. M. G. (1999). La fuerza: Fundamentación, valoración y entrenamiento. España: Gymnos.

Marins, J. C. B., & Giannichi, R. S. (1996). Avaliação e prescrição de atividade física: Guia prático. Rio de Janeiro: Shape.

Mayhew, J. L., Prinster, J. L., Ware, J. S., Zimmer, D. L., Arabas, J. R., & Bemben, M. G. (1995). Muscular endurance repetitions to predict bench press strength in men of different training levels. Journal of Sports Medicine and Physical Fitness, 35, 108-113.

Mayhew, J. L., Ware, J. R., & Prinster, J. L. (1993). Using lift repetitions to predict muscular strength in adolescent males. Journal of Strength and Conditioning Research, 15(6), 35-38.

Myer, G. D., Ford, K. R., Palumbo, J. P., & Hewett, T. E. (2005). Neuromuscular training improves performance and lower-extremity biomechanics in female athletes. Journal of Strength and Conditioning Research, 19(1), 51-60.

O’Conner, B., Simmons, J., & O’Shea, P. (1989). Weight training today. Saint Paul, MN: West Publisher.

Pereira, M. I. R., & Gomes, P. S. C. (2003). Testes de força e resistência muscular: Confiabilidade e predição de uma repetição máxima – Revisão e novas evidências. Revista Brasileira de Medicina do Esporte, 9(5), 325-335.        [ Links ]

Ploutz-Snyder, L. L., & Giamis, E. L. (2001). Orientation and familiarization to 1-RM strength testing in old and young women.Journal of Strength and Conditioning Research, 15(4), 519-523.

Rose, K., & Ball, T. E. (1992). A field test for predicting maximum bench press lift of college women. Journal of Applied Sport Science Research,69, 103-106.

 

Endereço para correspondência:

João Paulo Brito, ESDRM – Instituto Politécnico de Santarém, Pavilhão Multiusos, 1º piso, nave Norte, Av. Dr. Mário Soares, 2040-413 Rio Maior, Portugal.

E-mail: jbrito@esdrm.pt

 

Submetido: 13.09.2009 | Aceite: 25.04.2010