ORIGINAL ARTICLE

Comparison of predictive equations for resting metabolic rate in Portuguese women

José M. Tallon¹, Janine Narciso², Raquel Saavedra¹, António J. Silva^1,3, Ana Barros^1,4, Aldo M. Costa^2,3,5[*]

¹ University of Trás-os-Montes and Alto Douro, Vila Real, Portugal

² University of Beira Interior, Covilhã, Portugal

³ Research Centre in Sports, Health and Human Development, CIDESD, Portugal

⁴ Portugal Centre for the Research and Technology of Agro-Environmental and Biological Sciences, CITAB, Portugal

⁵ Health Science Research Center, CICS-UBI, Portugal

Endereço para correspondência | Dirección para correspondencia | Correspondence

---

 

ABSTRACT

Obesity represents a public health challenge, and dietary interventions to prevent or treat Obesity rely on the ability to accurately determine daily energy requirements - which are based on measures of total energy expenditure. Several prediction equations to estimate resting metabolic rate (RMR) have been developed, however, the validity of these equations is uncertain. The present study aims to determine the accuracy of four commonly used RMR prediction equations in normal weight, overweight and obese Portuguese women aged 18 to 64 years. RMR was measured in 156 women (age: 40.3 ± 10.2 years; Body Mass Index (BMI): 20.6 ± 6.8 kg/m²) using indirect calorimetry. The resulting values were compared with the predictive values from the Harris-Benedict, FAO/WHO/UNU, Schofield and Mifflin-St. Jeor equations across BMI categories. At an individual level, the equations with the highest percentage of accurate predictions were the Mifflin-St. Jeor equation in normal-weight women (41.9%) and the Harris-Benedict equation in overweight (55.4%) and obese (50.9%) women. The accuracy of the RMR prediction equations studied varied by weight status, and due to the low levels of accuracy reported, the present equations might have limited applicability for Portuguese women at an individual level.

Keywords: resting metabolic rate; indirect calorimetry; predictive equations; overweight; Obesity

---

 

Introduction

Obesity is one of the most serious public health challenges of the century, and it primarily arises from an imbalance between energy intake and expenditure (Omoleke, 2011; WHO, 2018). This imbalance may result from a complex combination of several factors that vary from one person to another, but it is particularly linked to an increased intake of food and a decrease in physical activity (WHO, 2018). Therefore, it is no surprise that most of obesity interventions have targeted these two behaviours, as nutritional interventions combined with physical activity are among the best strategies to treat Obesity (Jakicic & Otto, 2005; Peirson et al., 2014). Dietary interventions to prevent or treat Obesity rely on the ability to determine daily energy requirements accurately. Thus, understanding the total energy expenditure (TEE) of individuals is of extreme importance, as it constitutes a practical method to obtain estimates of energy requirements (Krüger et al., 2014; Nhung et al., 2005).

The three main components of TEE in humans are resting energy expenditure (REE), the thermic effect of food, and physical activity energy expenditure (Hall et al., 2012). REE is the rate of energy expenditure at rest, and it is the largest contributor to TEE, comprising approximately two-thirds of TEE (Hall et al., 2012). The terms basal metabolic rate (BMR) and resting metabolic rate (RMR) are used to define REE and are commonly confused with each other, although they vary by approximately 10%. BMR is measured shortly after participants wake up, succeeding an overnight stay in a research facility or metabolic chamber, while RMR is obtained when participants arrive at the research facility in the morning (Miller et al., 2013). Thus, successful interventions designed for weight loss or to prevent weight gain must focus on the accurate determination of the total contribution of individual REE to TEE (Sabounchi et al., 2013; Villareal et al., 2005).

Among the techniques used to measure metabolic rate, indirect calorimetry (IC) is one of the most accurate and noninvasive methods (Gupta et al., 2017); it assesses energy expenditure by measuring real-time oxygen consumption (VO₂) and carbon dioxide production (VCO₂) (Lam & Ravussin, 2017). However, this method is not usually available in the clinical setting as it is costly, time-consuming, and requires specialized trained staff for its execution (Carpenter et al., 2015; Schoeller, 2007). For these reasons, several predictive equations have been developed and are commonly used as an alternative to estimate REE (Carpenter et al., 2015; Weijs, 2008), with the Harris-Benedict, Schofield, Mifflin-St. Jeor and Food and Agriculture Organization/World Health Organization/United Nations University (FAO/WHO/UNU) equations being amongst the most used (Frankenfield et al., 2005; Müller et al., 2004). These prediction equations were developed between 1918 (Harris & Benedict, 1918) and 1990 (Mifflin et al., 1990), and were based on specific individual cohorts whose characteristics differ from our present-day population (Amaro-Gahete et al., 2018). Therefore, the validity of these equations is uncertain. Furthermore, for obese adults, the accuracy of prediction equations appears to be smaller when compared with their non-obese counterparts (Frankenfield et al., 2005). The level of overweight might be an important factor to consider in the accuracy of predictive equations, however, only a minority of studies have validated predictive equations for overweight and obese individuals separately (Weijs, 2008).

Hence, the present study aims to determine the accuracy of four RMR prediction equations: Harris-Benedict (Harris & Benedict, 1918), Schofield [weight] (Schofield, 1985), FAO/WHO/UNU (Food and Agricultural Organization/World Health Organization/United Nations University, 1985) and Mifflin-St. Jeor (Mifflin et al., 1990) in normal weight, overweight and obese Portuguese women aged 18 to 64 years.

Method

Participants

This cross-sectional study collected data from 156 healthy women aged between 18 and 64 years old, that attended a healthcare facility (Lisbon, Portugal) between October 2015 and July 2018 and agreed to participate in the study. Subjects were excluded if: (i) they had any medical conditions or were taking any medication that could affect RMR; (ii) they were enrolled in a weight loss program during the previous month; and (iii) they practiced intense exercise. All participants signed an informed consent form before the beginning of the study. Ethical approval was granted by the Ethical Committee of the Centro Hospitalar da Cova da Beira, Covilhã, Portugal (ethic code number 50/2016), and all study procedures were conducted in accordance with the Helsinki Declaration.

Procedures

Anthropometric measures

Height and weight of the subjects were measured and recorded before the test. Bodyweight was measured to the nearest 0.1kg using a SECA 803 scale, wearing light clothes and no shoes. Height was measured to the nearest 0.1 cm, using a SECA 213 stadiometer. BMI was calculated as weight divided by height squared (kg/m²), and its classification was made according to the WHO guidelines (World Health Organization, 2019). However, in the present study, Obesity comprised individuals with class I, class II, and class III Obesity.

RMR measurement

IC (FitMate^TM Pro equipment, COSMED, Italy) was used to measure RMR. The reliability and validity of COSMED’s FitMate^TM to measure RMR in adults have been reported elsewhere (Nieman et al., 2006; Vandarakis et al., 2013). Participants were instructed to avoid vigorous physical activity in the previous examination day and to maintain their normal dietary pattern. The consumption of alcoholic and caffeinated drinks and stimulants was not allowed in the 36 hours prior to the examination. Additionally, participants were instructed to fast for at least 5 hours prior to the test. The room temperature was kept neutral (≈21 ºC) in order to minimize measurement errors, and a respiratory quotient (RQ) of 0.85 was used as recommended by the manufacturer. The test was conducted at ≈12 PM, and participants were at rest in a supine position for 50 minutes prior to the start of the procedure. Before each test, the equipment was automatically calibrated according to the manufacturer’s specifications. VO₂ was determined at 30 seconds intervals for 13 minutes; values from the first 3 minutes were not considered for analysis.

RMR predictive equations

Four published predictive equations were used to estimate the RMR. These equations were: Harris-Benedict (Harris & Benedict, 1918), Schofield[weight] (Schofield, 1985), FAO/WHO/UNU (Food and Agricultural Organization/World Health Organization/United Nations University, 1985) and Mifflin-St. Jeor (Mifflin et al., 1990). All the predictive equations used can be found in Table 1.

 

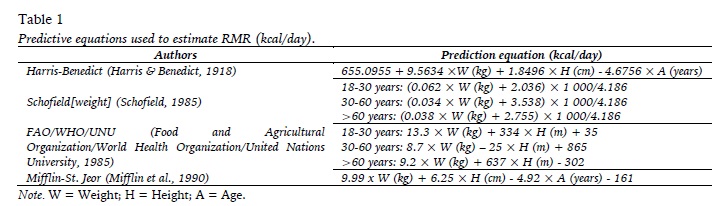
(clique para ampliar ! click to enlarge)

 

Statistical analysis

All data were analyzed using SPSS, version 24.0 (IBM® Corp., Armonk, NY, USA). Standard statistical methods were used for the descriptive statistics (mean ± Standard Deviation (SD) and median ± Interquartile range (IQR)) and statistical significance was set at p<0.05. The one-way ANOVA was used to determine if there were any statistically significant differences across BMI categories in age, height, BMI, and measured RMR. The Tukey HSD post-hoc test (if the data met the homogeneity of variance assumption) and the Games-Howell post-hoc test (if the data did not meet the homogeneity of variance assumption) were used to assess where the differences existed between the groups.

A paired t-test or a Wilcoxon ranked test was performed to compare the differences between measured (by IC) and estimated (by prediction equations) RMR. However, because group mean data masks individual errors (Frankenfield et al., 2005) and the assessment of individual energy requirements is a common practice by dietitians, a measure of accuracy on an individual level was defined as the main outcome of this study (Weijs, 2008). Therefore, prediction accuracy was defined as the percentage of individuals whose predicted RMR was between 90 and 110% of the measured RMR (Amaro-Gahete et al., 2018; Miller et al., 2013). Underprediction and overprediction were considered when estimated values of RMR were below 90% and above 110% of the measured RMR, respectively (Amaro-Gahete et al., 2018; Miller et al., 2013). Additionally, the absolute error (│measured RMR - predicted RMR│) and relative error (│measured RMR - predicted RMR│/ measured RMR × 100) in absolute values, between measured and estimated RMR were calculated.

Results

The characteristics of the study sample (Mean ± SD) are summarized in Table 2. The mean age of the participants was 40.3 ± 10.2 years. Their mean height and BMI were 163.5 ± 6.8 cm and 28.6 ± 5.7 kg/m², respectively. The participants’ mean RMR measured by IC was 1 463.7 ± 358.6 kcal/day. There were significant differences across BMI categories for all variables. Obese women (1 600.1 ± 425.6 kcal/day) had a significantly higher RMR than their normal weight (1 377.0 ± 313.7 kcal/day) and overweight (1 391.4 ± 268.9 kcal/day) counterparts.

 

(clique para ampliar ! click to enlarge)

 

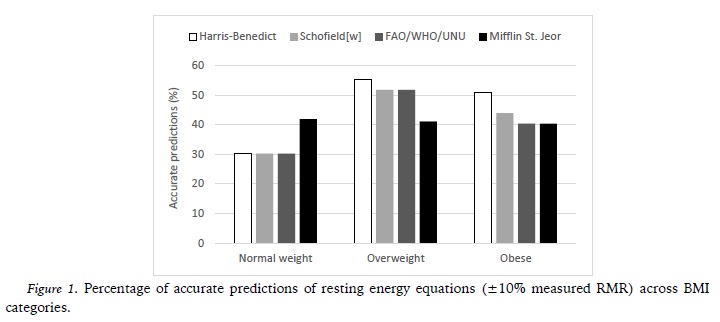
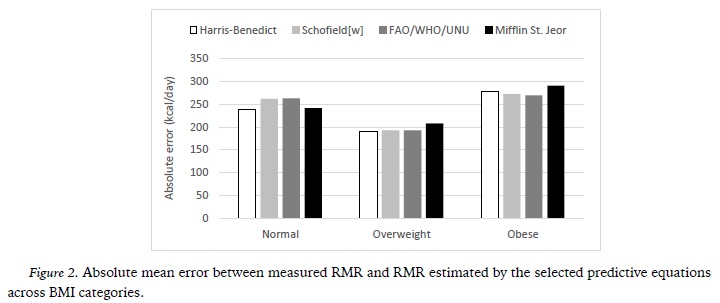
Table 3 shows the results of the comparison between measured and estimated RMR in normal-weight women. No significant differences were found between measured RMR and RMR estimated by the four equations. The Mifflin-St. Jeor equation provided the highest percentage of accurate RMR predictions (41.9%), while the remaining prediction equations only had 30.2% of accurate RMR predictions. These results are visually supported by Figure 1. For all prediction equations, underestimates were more common than overestimates. The Mifflin-St. Jeor and Harris-Benedict equations had slightly lower absolute errors (242.1 and 238.7 kcal/day, respectively) and relative errors (18.5 and 19.4%, respectively) than the Schofield and FAO/WHO/UNU equations. This data is also supported by Figure 2.

 

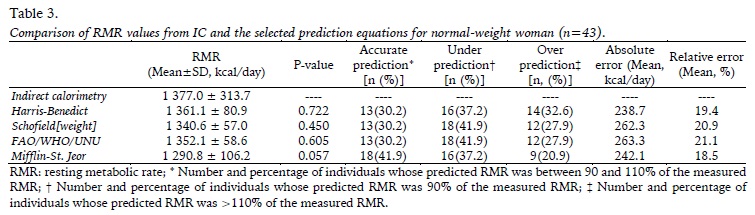
(clique para ampliar ! click to enlarge)

 

(clique para ampliar ! click to enlarge)

 

(clique para ampliar ! click to enlarge)

 

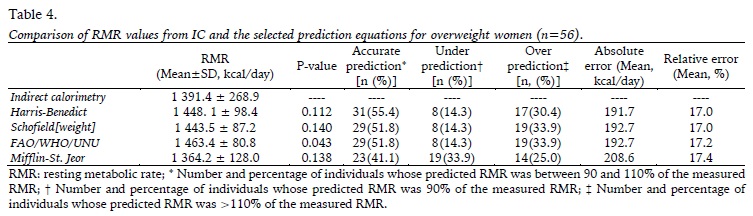
Table 4 shows the results of the comparison between measured and estimated RMR in overweight women. Significant differences were only found between measured and estimated RMR by the FAO/WHO/UNU equation (1 391.4 ± 268.9 versus 1 463.4 ± 80.8 kcal/day; P=0.043). The Harris-Benedict equation provided the highest percentage of accurate RMR predictions (55.4%), while the Mifflin-St. Jeor equation provided the lowest percentage of accurate RMR predictions (41.1%). (Figure 1) For most of the prediction equations, overestimates were more frequent than underestimates, except for the Mifflin-St. Jeor equation where errors tended to be underestimated. The Harris-Benedict equation had a slightly lower mean absolute error (191.7 kcal) than the remaining prediction equations (Figure 2).

 

(clique para ampliar ! click to enlarge)

 

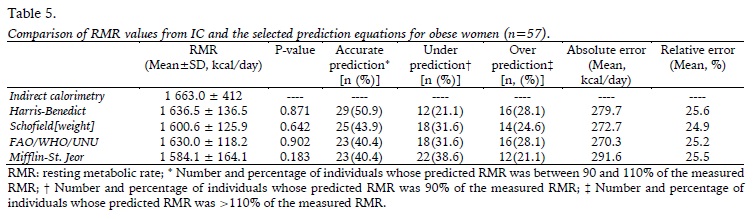
The results of the comparison between measured and estimated RMR in obese women are shown in table 5. For all four RMR prediction equations, no significant differences were found when compared to measured RMR. The Harris-Benedict equation provided the highest percentage of accurate RMR predictions (50.9%). (Figure 1) For most of the prediction equations, underestimates were more frequent than overestimates, except for the Harris-Benedict equation, where errors tended to be overestimated. Both absolute and relative errors of all the formulas were higher in this group. (Figure 2).

 

(clique para ampliar ! click to enlarge)

 

Discussion

Adequate estimation of an individual’s energy requirements is a fundamental component of dietary assessment since an imbalance between energy intake and expenditure can have serious health implications (Compher et al., 2006). Therefore, the validity of RMR predictive equations has been under debate for centuries, particularly in obese individuals (Ruiz et al., 2011). In this study, we assessed the accuracy of various predictive equations in normal weight, overweight and obese women by comparing the predicted RMR with the one measured by IC.

In normal-weight and obese participants, all four RMR prediction equations showed no significant differences when compared to measured RMR. In overweight participants, only the FAO/WHO/UNU equation significantly overpredicted RMR (1 463.4 ± 80.8 versus 1 391.4 ± 268.9 kcal/day; P=0.043). At an individual level, from the four equations studied the one with the highest percentage of accurate predictions for normal-weight women was the Mifflin equation (prediction accuracy: 41.9%) and for overweight and obese women was the Harris-Benedict equation (prediction accuracy: 55.4% and 50.9%, respectively). The Mifflin equation showed the highest prediction accuracy consistency across BMI categories (normal weight: 41.9%; overweight: 41.1% and Obesity: 40.4%). Mean absolute and relative errors of the four predictive equations were higher in the obese category.

Even though examining differences in RMR across BMI categories is out of the scope of this article, we would like to mention that obese women (1 600.1 ± 425.6 kcal/day) had a significantly higher RMR than normal weight (1 377.0 ± 313.7 kcal/day) and overweight (1 391.4 ± 268.9 kcal/day) women. Similarly, a recent review that included 21 studies assessing differences in REE between non-obese and obese adults reported that in most studies, REE was significantly higher in obese subjects (Carneiro et al., 2016). However, these findings may simply result from a lack of adjustment for body composition (Carneiro et al., 2016). Muller et al. (Müller et al., 2004) also found a higher REE in obese women when compared to their normal weight and overweight counterparts, but after adjusting for fat free-mass and fat mass this was no longer verified.

The mean absolute error and the percentage of accurate RMR predictions underestimate and overestimate for the Schofield and FAO/WHO/UNU were the most similar since the FAO/WHO/UNU equations were developed using a proportion of the Schofield database (Schofield, 1985; Schofield, 1985). The database compiled by Schofield resulted from an extensive literature review that included 114 published studies of BMR (n=11 000) from approximately 23 countries (Schofield, 1985; Schofield, 1985). However, a noteworthy feature of the Schofield database and, consequently, of the FAO/WHO/UNU database, is the large number of Italian individuals who have a higher BMR per kilogram when compared with other Caucasian groups (Hayter & Henry, 1994; Henry, 2005). Therefore, this might, in part, explain the low level of accurate RMR predictions of these two equations across BMI categories.

The Harris-Benedict equation is the oldest of the equations studied here and was developed using mainly young, normal-weight women (n=103; age range=15-74 years) and men (n=136; age range=16-63 years) (Harris & Benedict, 1918). Therefore, it was surprising that in the current study, the Harris-Benedict equation was the most accurate for overweight and obese Portuguese women - albeit only 55.4% and 50.9% of overweight and obese individuals had accurate predictions. In a comprehensive review conducted by Frankenfield et al. (Frankenfield et al., 2005) the Harris-Benedict equation has been shown to accurately predict RMR in 38 to 64% of obese subjects and overestimation errors were more common than underestimates, which is in accordance with our findings for this weight category. Similarly to our findings, a recent systematic review conducted by Madden et al. (Madden et al., 2016) found that the Harris-benedict equation was the most precise for overweight individuals (62.7% within 10% of measured RMR). Additionally, examined which of 27 predictive equations was the most adequate for normal weight to morbidly obese Belgian women (n=536; 18-71 years) and reported that both, the Harris-Benedict and the Mifflin equations provided accurate predictions in a wide BMI range (18.5-50kg/m²). However, caution is necessary when applying the Harris-Benedict equation in obese adults using adjusted body weight. Frankenfield et al. (Frankenfield et al., 2003) reported that the use of adjusted body weight reduced the level of overestimation of the equation, however, the error rate increased from 36% to 74% using actual body weight and adjusted body weight, respectively.

The Mifflin-St. Jeor equation was derived in 1980, from a sample of 498 normal weight, overweight and obese subjects (n=247 women), whose ages ranged from 19 to 78 years (Mifflin et al., 1990). This equation was proposed by the American Dietetic Association as being the most accurate (±10% of measured RMR) to estimate RMR in either non-obese (82% accurate predictions; age range 18-78 years) and obese (78% of accurate predictions; age range 19-69 years) adults aged 20 to 78 years in comparison with the Harris-Benedict and Owen equations (Frankenfield et al., 2005). However, the results were only based on one validation study - albeit of strong design - and the authors acknowledged that limited evidence exists to support the use of the Mifflin equation in overweight and obese individuals (Frankenfield et al., 2005; Weijs & Vansant, 2010). Weijs et al. (2008) studied the validity of 27 predictive equations for overweight and obese Dutch and American adults aged 18-65 years. They concluded that in American adults, almost 80% could be accurately predicted using the Mifflin equation, however for Dutch adults, none of the prediction equations were accurate. The Mifflin-St. Jeor equation has also been proposed to be the most accurate to estimate RMR in obese Spanish women (30 kg/m²>BMI<40 kg/m²) prior to a diet intervention (Ruiz et al., 2011) and in extremely obese women (Dobratz et al., 2007).

On the other hand, other equations have been proposed as the most accurate to estimate RMR. Miller et al. (2013) compared the accuracy of six RMR predictive equations to IC in 38 Hispanic women (age: 30 ± 7 years; 60% of the sample was overweight or obese) and found that the Owen equation had the highest percentage of accurate predictions (84.2%). A recent study assessing the accuracy of 33 REE predictive equations in 73 normal middle-aged adults stratified by weight categories, reported that the FAO/WHO/UNU (50% of prediction accuracy), the Livingston (46.9% of prediction accuracy) and the Owen (52.9% of prediction accuracy) equations were the most accurate for normal weight, overweight and obese adults, respectively (Amaro-Gahete et al., 2018).

Hence, no consensus appears to exist in the literature as to which equation is the best to predict RMR. This might, in part, be explained by the methodological differences between the studies and the heterogeneity of the cohorts being studied regarding, e.g., age, race/ethnicity, and gender (Hasson et al., 2011; Weijs & Vansant, 2010).

The present study is not without limitations. Only BMI was used to classify the weight status of the participants. The accuracy of only four equations that take into consideration age, height and/or weight to predict RMR was studied. Therefore, these equations do not account for body composition, specifically for fat-free mass, a major determinant of REE (Carneiro et al., 2016). It is also possible that other predictive equations not evaluated here could show a higher accuracy for RMR estimation in Portuguese women. Furthermore, we did not assess if all women were in the same phase of the menstrual cycle, as RMR fluctuations have been reported to occur during the menstrual cycle (Bisdee et al., 1989). Even though smokers were not excluded from the study, smoking was not allowed in the 36 hours prior to the test. It is also important to note that COSMED’s FitMate^TM does not include a carbon dioxide analyzer and, therefore, estimates RMR by using an RQ of 0.85 (Nieman et al., 2006; Vandarakis et al., 2013). However, the use of this fixed value of RQ has been reported to introduce little error in RMR estimation (Nieman et al., 2006; Vandarakis et al., 2013). The use of this value would be inappropriate if the test was performed after an extended period of fasting (12 hours or more) or in a state of abnormal metabolic distress (Vandarakis et al., 2013), which was not the case. Lastly, the sample of our study was relatively small. Therefore, further research with larger sample sizes that evaluates the validity of a larger number of RMR predictive equations is warranted to identify if a most suitable equation exists for Portuguese women or if the development of a new equation is required.

Conclusion

Even though at a population level, most of the equations studied did not show any statistically significant differences between measured and predicted RMR across BMI categories, at an individual level - which was the main outcome of this study - all the equations studied showed low levels of accuracy. Therefore, the application of these equations to Portuguese female individuals in dietetics practice might result in a considerable number of over and underestimations. In conclusion, the accuracy of the RMR prediction equations studied varied by weight status, and due to the low levels of accuracy reported here, the present equations might have limited applicability for Portuguese women at an individual level.

 

REFERENCES

Amaro-Gahete, F., Jurado-Fasoli, L., De-la-O, A., Gutierrez, Á., Castillo, M., & Ruiz, J. (2018). Accuracy and Validity of Resting Energy Expenditure Predictive Equations in Middle-Aged Adults. Nutrients, 10(11), 1635. https://doi.org/10.3390/nu10111635        [ Links ]

Bisdee, J. T., James, W. P. T., & Shaw, M. A. (1989). Changes in energy expenditure during the menstrual cycle. British Journal of Nutrition, 61(2), 187-199. https://doi.org/10.1079/BJN19890108        [ Links ]

Carneiro, I. P., Elliott, S. A., Siervo, M., Padwal, R., Bertoli, S., Battezzati, A., & Prado, C. M. (2016). Is Obesity Associated with Altered Energy Expenditure? Advances in Nutrition, 7(3), 476-487. https://doi.org/10.3945/an.115.008755        [ Links ]

Carpenter, A., Pencharz, P., & Mouzaki, M. (2015). Accurate Estimation of Energy Requirements of Young Patients. Journal of Pediatric Gastroenterology and Nutrition, 60(1), 4-10. https://doi.org/10.1097/MPG.0000000000000572        [ Links ]

Compher, C., Frankenfield, D., Keim, N., & Roth-Yousey, L. (2006). Best Practice Methods to Apply to Measurement of Resting Metabolic Rate in Adults: A Systematic Review. Journal of the American Dietetic Association, 106(6), 881-903. https://doi.org/10.1016/j.jada.2006.02.009        [ Links ]

Dobratz, J. R., Sibley, S. D., Beckman, T. R., Valentine, B. J., Kellogg, T. A., Ikramuddin, S., & Earthman, C. P. (2007). Predicting Energy Expenditure in Extremely Obese Women. Journal of Parenteral and Enteral Nutrition, 31(3), 217-227. https://doi.org/10.1177/0148607107031003217        [ Links ]

Food and Agricultural Organization/World Health Organization/United Nations University. (1985). Energy and protein requirements. Report of a Joint FAO/WHO/ UNU Expert Consultation. World Health Organization Technical Report Series 724.         [ Links ]

Frankenfield, D. C., Rowe, W. A., Smith, J. S., & Cooney, R. N. (2003). Validation of several established equations for resting metabolic rate in obese and non-obese people. Journal of the American Dietetic Association, 103(9), 1152-1159. https://doi.org/10.1053/jada.2003.50575        [ Links ]

Frankenfield, D., Roth-Yousey, L., & Compher, C. (2005). Comparison of Predictive Equations for Resting Metabolic Rate in Healthy Nonobese and Obese Adults: A Systematic Review. Journal of the American Dietetic Association, 105(5), 775-789. https://doi.org/10.1016/j.jada.2005.02.005        [ Links ]

Gupta, R., Ramachandran, R., Venkatesan, P., Anoop, S., Joseph, M., & Thomas, N. (2017). Indirect calorimetry: From bench to bedside. Indian Journal of Endocrinology and Metabolism, 21(4), 594. https://doi.org/10.4103/ijem.IJEM_484_16        [ Links ]

Hall, K. D., Heymsfield, S. B., Kemnitz, J. W., Klein, S., Schoeller, D. A., & Speakman, J. R. (2012). Energy balance and its components: Implications for body weight regulation. The American Journal of Clinical Nutrition, 95(4), 989-994. https://doi.org/10.3945/ajcn.112.036350        [ Links ]

Harris, J. A., & Benedict, F. G. (1918). A Biometric Study of Human Basal Metabolism. Proceedings of the National Academy of Sciences of the United States of America, 4(12), 370-373.         [ Links ]

Hasson, R. E., Howe, C. A., Jones, B. L., & Freedson, P. S. (2011). Accuracy of four resting metabolic rate prediction equations: Effects of sex, body mass index, age, and race/ethnicity. Journal of Science and Medicine in Sport, 14(4), 344-351. https://doi.org/10.1016/j.jsams.2011.02.010        [ Links ]

Hayter, J. E., & Henry, C. J. (1994). A re-examination of basal metabolic rate predictive equations: The importance of geographic origin of subjects in sample selection. European Journal of Clinical Nutrition, 48(10), 702-707.         [ Links ]

Henry, C. (2005). Basal metabolic rate studies in humans: Measurement and development of new equations. Public Health Nutrition, 8(7a), 1133-1152. https://doi.org/10.1079/PHN2005801        [ Links ]

Jakicic, J. M., & Otto, A. D. (2005). Physical activity considerations for the treatment and prevention of Obesity. The American Journal of Clinical Nutrition, 82(1), 226S-229S. https://doi.org/10.1093/ajcn/82.1.226S        [ Links ]

Krüger, R. L., Lopes, A. L., Gross, J. D. S., Macedo, R. C. O., Teixeira, B. C., & Reischak-Oliveira, Á. (2014). Validação de equações de predição da taxa metabólica basal em sujeitos eutróficos e obesos. Revista Brasileira de Cineantropometria e Desempenho Humano, 17(1), 73. https://doi.org/10.5007/1980-0037.2015v17n1p73        [ Links ]

Lam, Y. Y., & Ravussin, E. (2017). Indirect calorimetry: An indispensable tool to understand and predict Obesity. European Journal of Clinical Nutrition, 71(3), 318-322. https://doi.org/10.1038/ejcn.2016.220        [ Links ]

Madden, A. M., Mulrooney, H. M., & Shah, S. (2016). Estimation of energy expenditure using prediction equations in overweight and obese adults: A systematic review. Journal of Human Nutrition and Dietetics, 29(4), 458-476. https://doi.org/10.1111/jhn.12355        [ Links ]

Mifflin, M. D., St Jeor, S. T., Hill, L. A., Scott, B. J., Daugherty, S. A., & Koh, Y. O. (1990). A new predictive equation for resting energy expenditure in healthy individuals. The American Journal of Clinical Nutrition, 51(2), 241-247. https://doi.org/10.1093/ajcn/51.2.241        [ Links ]

Miller, S., Milliron, B.-J., & Woolf, K. (2013). Common Prediction Equations Overestimate Measured Resting Metabolic Rate in Young Hispanic Women. Topics in Clinical Nutrition, 28(2), 120-135. https://doi.org/10.1097/TIN.0b013e31828d7a1b        [ Links ]

Müller, M. J., Bosy-Westphal, A., Klaus, S., Kreymann, G., Lührmann, P. M., Neuhäuser-Berthold, M., Noack, R., Pirke, K. M., Platte, P., Selberg, O., & Steiniger, J. (2004). World Health Organization equations have shortcomings for predicting resting energy expenditure in persons from a modern, affluent population: Generation of a new reference standard from a retrospective analysis of a German database of resting energy expe. The American Journal of Clinical Nutrition, 80(5), 1379-1390. https://doi.org/10.1093/ajcn/80.5.1379        [ Links ]

Nhung, B. T., Khan, N. C., Hop, L. T., Lien, D. T. K., Le, D. S. N. T., Hien, V. T. T., Kunii, D., Sakai, T., Nakamori, M., & Yamamoto, S. (2005). FAO/WHO/UNU equations overestimate resting metabolic rate in Vietnamese adults. European Journal of Clinical Nutrition, 59(10), 1099-1104. https://doi.org/10.1038/sj.ejcn.1602199        [ Links ]

Nieman, D. C., Austin, M. D., Benezra, L., Pearce, S., McInnis, T., Unick, J., & Gross, S. J. (2006). Validation of Cosmed’s FitMate^TM in Measuring Oxygen Consumption and Estimating Resting Metabolic Rate. Research in Sports Medicine, 14(2), 89-96. https://doi.org/10.1080/15438620600651512        [ Links ]

Omoleke, S. A. (2011). Obesity: A major public health challenge of 21st century in the United Kingdom (UK). Journal of Public Health and Epidemiology, 3(12). https://doi.org/10.5897/JPHE11.159        [ Links ]

Peirson, L., Douketis, J., Ciliska, D., Fitzpatrick-Lewis, D., Ali, M. U., & Raina, P. (2014). Treatment for overweight and Obesity in adult populations: A systematic review and meta-analysis. CMAJ Open, 2(4), E306-E317. https://doi.org/10.9778/cmajo.20140012        [ Links ]

Ruiz, J. R., Ortega, F. B., Rodríguez, G., Alkorta, P., & Labayen, I. (2011). Validity of Resting Energy Expenditure Predictive Equations before and after an Energy-Restricted Diet Intervention in Obese Women. PLoS ONE, 6(9), e23759. https://doi.org/10.1371/journal.pone.0023759        [ Links ]

Sabounchi, N. S., Rahmandad, H., & Ammerman, A. (2013). Best-fitting prediction equations for basal metabolic rate: Informing obesity interventions in diverse populations. International Journal of Obesity, 37(10), 1364-1370. https://doi.org/10.1038/ijo.2012.218        [ Links ]

Schoeller, D. A. (2007). Making Indirect Calorimetry a Gold Standard for Predicting Energy Requirements for Institutionalized Patients. Journal of the American Dietetic Association, 107(3), 390-392.         [ Links ]

Schofield, C. (1985). An annotated bibliography of source material for basal metabolic rate data. Human Nutrition Clinical Nutrition, 39 Suppl 1, 42-91.         [ Links ]

Schofield, W. N. (1985). Predicting basal metabolic rate, new standards and review of previous work. Human Nutrition. Clinical Nutrition, 39 Suppl 1, 5-41.         [ Links ]

Vandarakis, D., Salacinski, A. J., & Broeder, C. E. (2013). A Comparison of Cosmed Metabolic Systems for the Determination of Resting Metabolic Rate. Research in Sports Medicine, 21(2), 187-194. https://doi.org/10.1080/15438627.2012.757226        [ Links ]

Villareal, D. T., Apovian, C. M., Kushner, R. F., & Klein, S. (2005). Obesity in Older Adults: Technical Review and Position Statement of the American Society for Nutrition and NAASO, The Obesity Society. Obesity Research, 13(11), 1849-1863. https://doi.org/10.1038/oby.2005.228        [ Links ]

Weijs, P. J. (2008). Validity of predictive equations for resting energy expenditure in US and Dutch overweight and obese class I and II adults aged 18-65 y. The American Journal of Clinical Nutrition, 88(4), 959-970. https://doi.org/10.1093/ajcn/88.4.959        [ Links ]

Weijs, P. J. M., & Vansant, G. A. A. M. (2010). Validity of predictive equations for resting energy expenditure in Belgian normal weight to morbid obese women. Clinical Nutrition, 29(3), 347-351. https://doi.org/10.1016/j.clnu.2009.09.009        [ Links ]

WHO. (2018). WHO | Obesity and overweight. WHO; World Health Organization.         [ Links ]

World Health Organization. (2019). Body mass index-BMI. World Health Organization. http://www.euro.who.int/en/health-topics/disease-prevention/nutrition/a-healthy-lifestyle/body-mass-index-bmi        [ Links ]

 

Endereço para correspondência | Dirección para correspondencia | Correspondence

^[*]Convento de Sto. António, 6201-001, Covilhã, Portugal. Email: amcosta@ubi.pt

 

Acknowledgments: We would like to show our gratitude to all the participants in this study for the time they devoted to our research.

Conflict of interests: Nothing to declare.

Funding: This article is part of the project “Causes4AdolescentObesity - The multifactorial nature of obesity: a preliminary study on the behavioral, physiological and genetic profile of Portuguese adolescents” (POCI-01-0145-feder-023813), which is funded by the Fundação para a Ciência e Tecnologia (https://www.fct.pt/) and co-funded by the Fundo Europeu de Desenvolvimento Regional (FEDER), through the Programa Operacional Competitividade e Internacionalização (COMPETE2020).

 

Manuscript received at December 17^th 2019; Accepted at February 8^th 2020