Método espacio-temporal para el reconocimiento de acciones humanas en el espacio canónico

 

I. Gómez-Conde ¹, D.N. Olivieri, X.A. Vila ¹

¹ Departamento de Informática, Universidad de Vigo. Edificio Politécnico, As Lagoas s/n 32004 Ourense (España) E-mail: ivangconde@uvigo.es, E-mail: olivieri@ei.uvigo.es, E-mail: anton@uvigo.es

 

RESUMEN

El reconocimiento de acciones humanas es un campo de investigación muy activo en visión artificial, donde los esfuerzos se centran actualmente en la detección de comportamientos humanos en vídeos en tiempo real. En este trabajo, se presenta un algoritmo espacio-temporal, que denominamos Motion Vector Flow Instance (MVFI) para la clasificación de acciones sobre vídeos, y se muestran los resultados de su aplicación a dos conjuntos de datos, “KTH" y “MILE”, que contienen escenas de acciones humanas con diferentes condiciones de grabación (varios ángulos de cámara, iluminación, diferentes prendas de vestir, calidad de vídeo…) La plantilla MVFI codifica la información de la velocidad del movimiento de una persona, a partir del flujo óptico que se obtiene en cada fotograma de un vídeo. A continuación, mediante aprendizaje supervisado, se proyectan las imágenes MVFI en el espacio canónico y se buscan los límites de decisión para varias acciones con máquinas de soporte vector (SVM). En este artículo, mostramos que este método para detectar acciones humanas, es robusto y permite un reconocimiento en tiempo real.

Palabras clave: reconocimiento de acciones humanas; visión por computador; análisis componentes principales; plantillas espacio-temporales

 

ABSTRACT

The recognition of human actions is a very active research field in computer vision, where efforts are presently focused on the detection of human behavior in real-time video. In this paper, we present a novel spatio-temporal algorithm, called the Motion Vector Flow Instance (MVFI), for classification of actions in videos. We show the results of applying this algorithm to two public datasets, "KTH" and "MILE" that contain scenes of human actions with different recording conditions (multiple camera angles, lighting, different clothes, and video quality). The MVFI spatio-temporal template encodes information about the speed and direction of human motion from the optical flow vectors obtained within each video frame. Then, by using supervised learning, MVFI images are projected into a canonical vector space and decision boundaries are determined for various actions by using a support vector machines (SVM) algorithm. Thus, in this paper, we demonstrate that our method is robust for detecting human actions across different datasets and provides real-time recognition.

Keywords: human action recognition; computer vision; principal component analysis; spatio-temporal templates

 

1. Introducción

La detección automática de acciones y gestos humanos sobre vídeos es un campo muy activo de investigación y presenta un interés creciente para empresas de diversos sectores. Por ejemplo, en el campo del cuidado de la salud, no existen sistemas automatizados que permitan monitorizar la actividad de una persona en todo momento. Existen algunos sistemas, como las pulseras de emergencia o la monitorización de los signos vitales de una persona, pero ninguno de ellos permite seguir la actividad de esa persona ni detectar automáticamente la acción que realiza. Los sistemas de videovigilancia actuales tampoco sirven al requerir de supervisión humana, puesto que no son capaces de detectar automáticamente la acción que realiza esa persona.

Clasificar acciones humanas es un problema complejo en visión artificial. Existen diferentes enfoques como son el seguimiento del cuerpo en 3D mediante múltiples cámaras, el uso de modelos para caracterizar las imágenes en 2D de un vídeo o el uso de imágenes que guardan el historial del movimiento de fotogramas anteriores. El artículo de Poppe (2010) ofrece una revisión reciente de este campo. Si nuestro objetivo es detectar tipos de movimiento, tales como actividades anormales o caídas, el seguimiento de la persona en 3D produce excesiva información y supone un elevado coste computacional. Una forma de reducir ese coste podría basarse en la reducción de la dimensionalidad de los datos del vídeo transformando una secuencia de imágenes en puntos en un espacio canónico, en el que se podrían distinguir formas de “andar” normales (Huang, 1999) de otras irregulares, como es el caso de las personas que padecen la enfermedad de Parkinson (Cho, 2010).

En este artículo se describe un algoritmo de visión artificial para la detección de actividades humanas usando una transformación en el autoespacio de las imágenes y se muestra su aplicación práctica para discriminar dos actividades muy comunes como son “andar” y “hacer footing”. En la sección 2 se analiza el estado del arte en el que se encuentra la detección y reconocimiento de acciones humanas en vídeos. A continuación, se describen las bases de datos de vídeo utilizadas para realizar los análisis y se detalla la plantilla espacio-temporal desarrollada así como las matemáticas asociadas a la transformación canónica. En el punto siguiente se comenta la metodología que se utilizó para dividir los vídeos en conjuntos de entrenamiento y conjuntos de test y finalmente, se presentan los resultados y conclusiones que se han obtenido de este trabajo.

 

2. Estado del arte

El reconocimiento de acciones humanas sobre vídeo es un problema antiguo para los investigadores en visión artificial, y ha madurado lo suficiente para permitir la existencia de varios artículos recientes que resumen las técnicas empleadas hasta el momento. Un ejemplo, es el artículo de Forsyth et. al. (2006) que han descrito la cinemática del seguimiento del cuerpo humano, y centran su interés en entender su movimiento. Más recientemente un extenso trabajo de Poppe (2010) describe los principales enfoques existentes para etiquetar acciones humanas sobre secuencias de vídeo.

Para describir el movimiento de todo el cuerpo humano, se han desarrollado varios sistemas que permiten realizar un seguimiento en 2-dimensiones y trasladarlo a 3-dimensiones. El trabajo de Deutscher (2005), por ejemplo, describe el uso de modelos con 26 ángulos de movilidad y usa filtros de partículas en cada nodo para reconstruir el movimiento del cuerpo humano al completo. Bobick et. al. (2001) se centran en el reconocimiento de actividades a través de la representación mediante plantillas de movimiento. Ellos introducen los conceptos de instancias de historial de movimiento (Motion History Instance MHI) y de instancias de energía de movimiento (Motion Energy Instance MEI) que permiten capturar información a través de muchas secuencias de imágenes. Existen otros métodos modernos como el que describen Meeds et. al. (2008) que usa modelos gráficos bayesianos para inferir modelos de actividades humanas y animales sin necesidad de conocimiento previo del tipo de movimiento. Ikizler y Forsyth (2008) han mostrado que los movimientos atómicos de las diferentes partes del cuerpo en 3-dimensiones, cuando son combinados con modelos ocultos de Markov (HMMs), pueden ser usados para inferir composiciones de movimientos, tales como la combinación de fonemas para construir palabras.

El objetivo de estos métodos es proporcionar una descripción completa del movimiento humano, pero son computacionalmente muy costosos para aplicaciones en tiempo real. Las técnicas basadas en información espacio-temporal son más adecuadas y eficientes en esos casos. La información espacio-temporal, dirección y sentido del movimiento, puede ser codificada en plantillas que representan el movimiento y permiten capturar características del mismo a través de diferentes fotogramas. Cuando se combinan con algoritmos para reducir la dimensionalidad de los datos, como análisis de componentes principales (PCA), estos métodos son capaces de clasificar diferentes tipos de movimientos. La idea tiene sus orígenes en el trabajo de Etemad y Chellappa (1997) para el reconocimiento de caras, quienes utilizaron análisis lineal discriminante (LDA), también llamado análisis canónico, para optimizar la separación de diferentes caras. La idea fundamental de este método es que, dado que las características esenciales de una cara son las mismas, es la covarianza la que juega un papel importante en la discriminación. Esta idea, aplicada a las transformaciones en los autoespacios para el movimiento humano, se utilizó por primera vez para diferenciar personas basándose en su forma de “andar”. Huang et. al. (1999) usaron PCA para clasificar formas de “andar” de diferentes personas. Ellos introducen la idea de una transformación en el autoespacio canónico, que consiste primero en aplicar PCA seguido de LDA para reducir la varianza entre los elementos de una clase mientras se maximiza la varianza entre los elementos de diferentes clases. Das et. al. (2006) usan PCA en dos etapas, donde la primera consiste en reducir la dimensionalidad y la segunda en comparar las curvas en el nuevo espacio. En una interesante aplicación de reconocimiento de formas de “andar”, Cho et. al. (2009) han mostrado el uso de PCA para analizar el grado de enfermedad de Parkinson en pacientes de avanzada edad basándose en su forma de “andar”.

 

3. Metodología

En nuestro algoritmo mediante aprendizaje supervisado, se entrena el sistema con varias secuencias de vídeo de diferentes acciones y diferentes actores. Estas secuencias son transformadas mediante las plantillas MVFI (Olivieri et. al., 2011) y posteriormente se mapean en diferentes puntos en el autoespacio. A continuación, se realizan una serie de transformaciones canónicas (PCA y LDA) para reducir drásticamente la dimensión de cada secuencia de imágenes a un conjunto de puntos en un espacio multidimensional mucho más pequeño.

Una vez que disponemos en el espacio canónico de la trayectoria de puntos de cada una de las acciones, se realiza un entrenamiento utilizando máquinas de soporte vector (SVM). Cada uno de los puntos es etiquetado en función de su categoría (“andar o “hacer footing”). El reconocimiento de una nueva secuencia de una acción consiste en formar la plantilla MVFI correspondiente y realizar la transformación al espacio canónico creado en el entrenamiento, para posteriormente determinar mediante la SVM si pertenece a una categoría u otra. En la Figura 1 se puede ver el flujo de trabajo de todo el proceso.

 

 

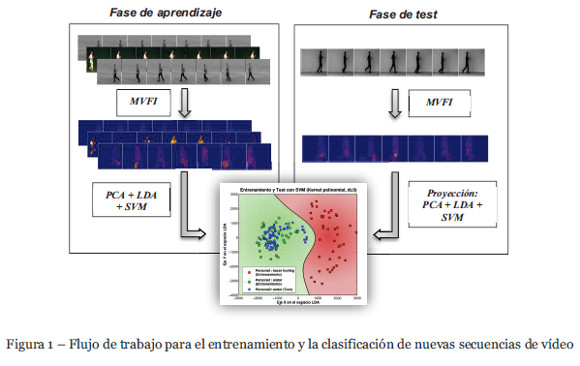
3.1. Conjuntos de datos: KTH y MILE

Hemos realizado un extenso entrenamiento y validación para evaluar el rendimiento del método propuesto. En la Figura 2 se pueden observar los dos tipos de acciones utilizadas para realizar el entrenamiento: “andar” y “hacer footing”. Se han utilizado dos conjuntos de datos: KTH-Human, una base de datos de vídeo pública y MILE-Human, creada por nosotros para realizar las pruebas.

 

 

KTH Human (Vapnik, 1995): este conjunto de vídeos contiene seis tipos de acciones: andar, hacer footing, correr, boxear, agitar las manos y aplaudir. En este trabajo sólo se utilizaron las acciones de “andar” y “hacer footing”. Tomamos los vídeos de 11 personas en tres tipos de escenarios diferentes: exteriores con ropa uniforme, exteriores con ropas diferentes e interiores. Todas las secuencias utilizadas fueron grabadas sobre fondos homogéneos con una cámara estática a una velocidad de 25 fotogramas por segundo. La duración media de cada secuencia es de 4 segundos y tienen una resolución de 160x120 píxels.

MILE Human (MILE, 2011): se trata de una base de datos de vídeo creada para realizar las pruebas con este nuevo algoritmo; contiene varios tipos de acciones: andar, hacer footing, sentarse, acostarse, caerse… En este artículo sólo se han utilizado dos acciones: “andar” y “hacer footing”. Se grabaron un total de 5 secuencias por cada acción, con 12 personas. Todas las actividades fueron grabadas utilizando la misma distancia focal a una velocidad de 25 fotogramas por segundo. La duración de cada uno de los vídeos es de 5 segundos de media y tiene una resolución de 572x512 píxels.

Se dividió el conjunto de vídeos en un conjunto de entrenamiento y un conjunto de test con diferente número de personas. Las imágenes han sido procesadas a bajo nivel para generar la plantilla de movimiento MVFI, utilizando programas escritos en Python con llamadas a funciones de la librería de visión artificial OpenCV2.1 (Bradski, 2008). Estos algoritmos procesan los vídeos y producen las secuencias de imágenes del movimiento: extraen la plantilla de movimiento de los fotogramas individuales, reducen el tamaño de las imágenes a 128x128 usando un algoritmo adaptativo de redimensionado, y finalmente las convierten a escala de grises para realizar la transformación al espacio canónico.

 

3.2. Plantilla espacio-temporal MVFI

La Instancia del Vector de Flujo de Movimiento (Motion Vector Flow Instance, MVFI) es un nuevo método espacio-temporal, desarrollado por nosotros (Olivieri et. al., 2011), que usa el flujo óptico para guardar la información de la magnitud de la velocidad y dirección del movimiento en cada fotograma. Muchas de las actividades que se realizan diariamente, se caracterizan por aumentos bruscos de velocidad en la dirección horizontal y/o vertical. Nuestra plantilla de movimiento codifica la información de la velocidad y dirección del movimiento para ser sensible a movimientos bruscos del cuerpo humano.

En primer lugar, caracterizamos el vídeo de entrada V (w, h, N_f) mediante su resolución (ancho w, alto h) y el número de fotogramas N_f para inicializar el vídeo de salida O(w, h) que contendrá la plantilla MVFI de ese movimiento. En cada instante de tiempo t el fotograma correspondiente (matriz con los valores en escala de grises de cada píxel) se divide en una cuadrícula que contiene el campo de flujo óptico, donde cada uno de los puntos de esa cuadrícula se representan por (x, y). En cada uno de esos puntos evaluamos el vector de movimiento (Figura 3a) a través de un algoritmo piramidal muy conocido (Farnebäck, 2003), y creamos un rectángulo por cada vector (Figura 3b). En cada instante t se inicializa una lista de objetos s para contener los vectores de flujo f en dicho instante. Por cada punto de la cuadrícula (x, y) en el flujo óptico, se almacenan en s los componentes del vector (fx, fy) junto con la magnitud ||f||. Posteriormente, ordenamos los vectores de s por la magnitud ||f||, para colocar los vectores de mayor peso al principio de la lista. Finalmente, se escribe el vídeo de salida, codificando cada vector de flujo óptico en s, desde el más pequeño al más grande, para asegurar que los vectores de flujo más grandes no sean sobrescritos por otros más pequeños. Cada uno de los rectángulos leídos de la lista, se codifican en función de la magnitud ||f|| como se muestra en la Figura 3b.

 

 

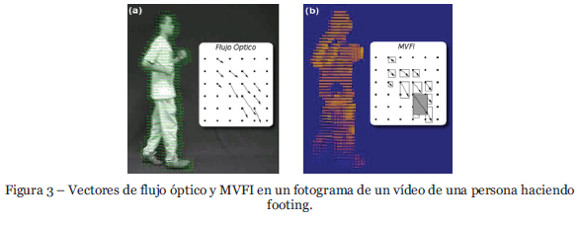
Nuestro método MVFI difiere del historial de flujo de movimiento (MHI) propuesto por Bobick y Davis (2001) en dos aspectos fundamentales. En primer lugar en que no se mantiene un historial de los x fotogramas anteriores, sino que usa una fotografía instantánea de los vectores de flujo en un instante t que permite codificar los cambios bruscos de velocidad más eficientemente. Y en segundo lugar, en que el tamaño de los vectores se codifica en el tamaño de los rectángulos, que son almacenadas en capas de tal forma que las velocidades mayores se almacenan en la cima. En la Figura 4 se puede observar el resultado de aplicar la plantilla MVFI sobre un vídeo de una persona haciendo footing. En nuestra página Web (MILE, 2011) se puede observar el resultado de aplicar la plantilla MVFI a diferentes tipos de acciones humanas.

 

 

3.3. Transformación canónica

Las transformaciones canónicas, basadas en PCA y LDA, se describen en la literatura científica y en recientes libros de texto (Fukunaga, 1990 y Gonzalez, 2003). Aquí resumiremos los detalles matemáticos de esta técnica, aplicados a nuestro problema particular, utilizando la notación estándar. En primer lugar, definimos una secuencia de movimiento s, que tiene N_f imágenes (o fotogramas) x_{i=1 … Nf} . A continuación, definimos un tipo de acción humana (clase) c, la cual puede estar formada por N_s secuencias de movimiento. Luego formamos un vector de entrenamiento con el conjunto de las secuencias de imágenes, pertenecientes a diferentes clases, en total tenemos N_c clases. Obtenemos así un vector X, donde cada elemento x _{k, i, ,j} , se corresponde con la imagen de la clase k perteneciente a la secuencia i, y al frame j. El número total de imágenes en X es N_T , con N_T = N_cN_sN_f. Por lo tanto, el conjunto de entrenamiento viene dado por el vector:

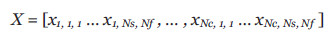
donde cada x_{k, i, j} es la matriz de píxels del fotograma j de la secuencia i de la clase k. El espacio PCA canónico se construye a partir de los vectores ortogonales que poseen la mayor varianza entre todas las imágenes en X. Por lo tanto, para construir el espacio PCA, debemos encontrar la media del vector X, dada por m_x, y la covarianza C_x, que representa la desviación de los píxels de la media:

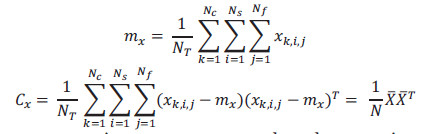
A partir de los vectores propios o autovectores u_i y los valores propios o autovalores 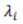de C_x se determinan las direcciones ortogonales con la mayor varianza:

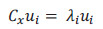
asumiendo que C_x puede ser diagonalizada. Teniendo en cuenta que es una matriz muy grande de n x n (n es el número total de píxels de ), existe una simplificación práctica y bien conocida (ver Descomposición en valores singulares en Fukunaga, 1990) que consiste en considerar la matriz relacionada 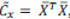, la cual es solamente N_T x N_T. Esta transformación permite calcular el nuevo conjunto de autovectores y autovalores 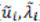. Se puede demostrar que este nuevo espacio de está relacionado con el espacio original de 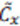a través de una simple transformación en X.

Utilizando la teoría estándar de PCA, este nuevo espacio es reducido a solamente los 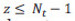autovalores de mayor peso 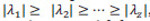, lo cual se justifica demostrando que 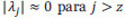. El conjunto parcial de autovectores forman un nuevo espacio y = [y_{1, 1, 1} . . . y_{Nc, Ns, Nf} ] en el que se representan las proyecciones de las imágenes originales:

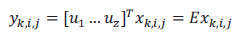
Esta técnica proporciona un método directo para proyectar las imágenes originales de las secuencias dentro de un nuevo espacio multidimensional, donde cada punto representa una imagen y una trayectoria representa una secuencia de imágenes. Para clasificar diferentes tipos de acciones humanas a partir de la transformación de secuencias de vídeo en puntos 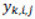en el nuevo espacio, aplicamos el conocido criterio de Fisher (Theodoridis, 2010) que usa la matriz de covarianza para maximizar la varianza entre diferentes clases (S_b), mientras que al mismo tiempo minimiza la varianza entre los elementos de la misma clase (S_w).

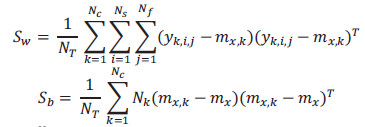
donde 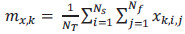Obtenemos así, una nueva base ortogonal 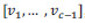, que toma los puntos 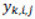del espacio PCA y los transforma en puntos del espacio LDA:

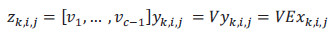
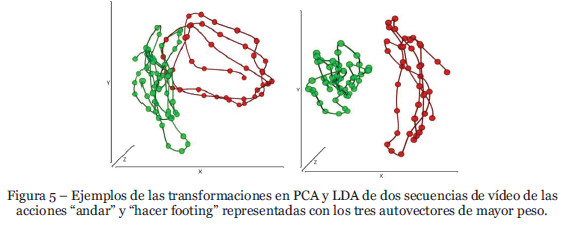
Hemos comprobado experimentalmente que, para obtener una buena clasificación, era suficiente la transformación en un nuevo espacio menor o igual a 10 dimensiones. En la Figura 5 se muestra los excelentes resultados que se obtienen con las transformaciones en PCA y LDA de dos secuencias de acciones de “andar” y “hacer footing” representadas con únicamente 3 dimensiones, los tres autovectores de mayor peso.

 

 

3.4. Entrenamiento

Para realizar el entrenamiento y la clasificación se dividió la base de datos de vídeo en la siguiente estructura: acción : persona: secuencia, donde acción representa las diferentes clases de movimiento, personas, son los diferentes sujetos que realizan la acción y secuencias es el conjunto de secuencias de vídeos procesados por acción y persona, y que utilizan la plantilla de movimiento espacio-temporal (MVFI). Todo ello constituye tres conjuntos para KTH (A_KTH, P_KTH, S_KTH ) y otros tres para MILE (A_MILE, P_MILE, S_MILE ) con un número total de (N_A=2 acciones, N_P =11 personas y N_S =4 secuencias por persona y acción) para KTH y (N_A =2 acciones, N_P =8 personas y N_S =4 secuencias por persona y acción) para MILE.

El entrenamiento se construyó encontrando todas las posibles combinaciones, como un producto cartesiano n-ario, a partir de los diferentes conjuntos definidos. Por ejemplo, un entrenamiento con todas las combinaciones de 2 clases con 3 personas y 1 secuencia por persona se representará como: T = [2][3][1].

El conjunto de test se obtiene considerando el mismo conjunto de acciones, A, pero usando el complemento de las secuencias de entrenamiento. De esta forma, el conjunto complementario, o conjunto de test, 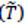, es calculado por:

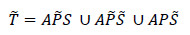
donde 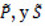, y son los complementarios a P y S respectivamente.

Para determinar la clase a la que pertenece una secuencia de test desconocida, se utiliza un clasificador de máquinas de vectores de soporte vector (SVM). Desde el punto de vista matemático, un conjunto de entrenamiento es de la forma:

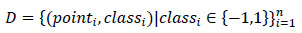
donde class_i es -1 o 1, indicando la clase a la que pertenece (“andar” o “hacer footing”) cada uno de los puntos point_i. Cada point_i es un vector de reales de Z-dimensiones. Y nosotros queremos encontrar el hiperplano que maximiza la distancia entre los puntos que tienen clase class_i = -1 de los que tienen clase class_i = 1.

El algoritmo original del hiperplano óptimo propuesto por Vapnik (1963) era un clasificador lineal. Sin embargo, Boser, Guyon y Vapnik (1992) sugirieron una manera de crear clasificadores no lineales aplicando un kernel para maximizar la separación entre los hiperplanos. En este artículo, se han analizado los resultados con varios kernels (lineal, cuadrático, gaussiano de base radial, polinomial y perceptrón multicapa). Los mejores resultados fueron presentados con el kernel polinomial que se define como: 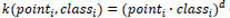donde es la dimensión del espacio del kernel. Se realizaron pruebas con diferentes valores para d, obteniendo los mejores resultados con un valor de d=3. Por lo tanto, todos los resultados presentados en este artículo se obtuvieron utilizando un kernel polinomial con d=3.

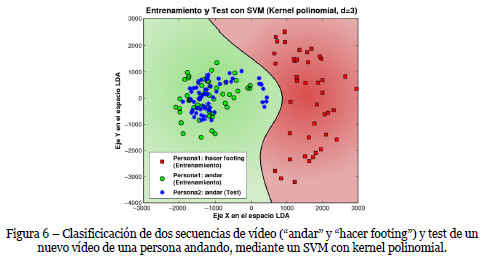
En la Figura 6 podemos ver el resultado de aplicar un SVM con un kernel polinomial (d=3) a un conjunto de datos de entrada. Vemos como todos los puntos de la nueva secuencia de test (aspas en la figura) son correctamente mapeados en la parte del espacio que el SVM clasifica como “andar".

 

 

4. Experimentos y resultados

Hemos realizado un entrenamiento con todas las posibles combinaciones de vídeos de las bases de datos que hemos utilizado. Analizamos la influencia de diferentes ropas, fisionomías y condiciones de luz (escenas de interior o exterior) así como el número de personas necesarias en el entrenamiento. En esta sección, presentamos los resultados más relevantes.

La tabla 1 muestra un resumen estadístico de algunas de las combinaciones de secuencias de vídeo utilizadas en el proceso de entrenamiento. La primera columna, es la combinación de entrenamiento: T = (N_acciones, N_personas, N_secuencias).

 

 

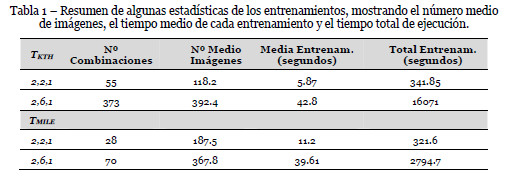
Como se puede apreciar, el número medio de fotogramas por secuencia varía en función de la base de datos de vídeo, aproximadamente 120 imágenes en KTH-Human y 187 en MILE-Human con N_p = 2. Al aumentar el número de personas en el entrenamiento (N_P =6) vemos como aumenta el número de imágenes en cada una de las combinaciones de entrenamiento a 390 en KTH-Human y 370 en MILE-Human aproximadamente. En ambas bases de dato de vídeo los tiempos medios de ejecución por entrenamiento están entre 6 y 11 segundos con entrenamientos del tipo (2, 2, 1) y aproximadamente 40 segundos en el caso de entrenamientos con 6 personas.

En el estudio realizado para este artículo se han analizado los resultados de entrenamiento y clasificación de acciones humanas tanto de KTH-Human como MILE-Human en función de algunos parámetros. Por ejemplo, comparamos las tasas de acierto en el reconocimiento de nuevas secuencias de vídeo en función del número de personas N_p incluidas en el entrenamiento comprobando que con sólo 6 personas se logró una tasa de acierto media de 97.48%

Para analizar la influencia de cambios en las bases de datos, hemos realizado una validación cruzada con todas las posibles combinaciones de entrenamiento y test posibles entre las dos bases de datos. En la tabla 2 se pueden observar todas las matrices de confusión para las combinaciones de entrenamiento y test. Por ejemplo, el caso 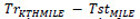hace referencia a los resultados obtenidos con un entrenamiento que incluye todas las combinaciones de vídeos de 6 personas y 1 secuencia por persona en KTH-Human y MILE-Human (T_KTH = (2,6, 1) y T_MILE = (2,6,1)). Posteriormente intentamos clasificar los vídeos que pertenecen al conjunto complementario del entrenamiento en la base de datos de vídeo de KTH-Human 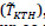, y obtuvimos un 99.44% de clasificaciones correctas para la acción de “andar” y un 93.75% para la acción de “hacer footing”.

 

 

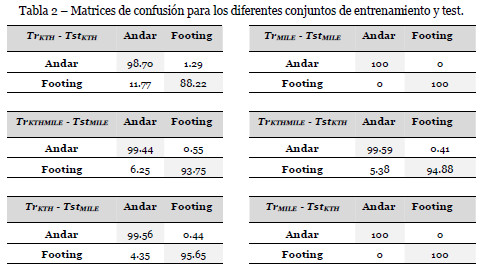
Se observó que los mejores resultados se obtuvieron entrenando y clasificando con nuestra propia base de datos de vídeo. Esto es debido a que todas las escenas fueron grabadas en el mismo lugar, las personas siempre se encontraban a la misma distancia de la cámara aproximadamente y no había cambio de ángulos. En KTH-Human sin embargo, se han utilizado vídeos con personas a diferentes distancias, escenas de interior y de exterior, lo cual justifica que los resultados no sean tan buenos.

La tabla 3 muestra los resultados obtenidos por diferentes estudios que han tratado de discriminar acciones y que han utilizado la base de datos de KTH para validación y test. Y más concretamente, que han comparado las acciones de “andar” y “hacer footing”. Como podemos apreciar nuestros resultados son mejores que en trabajos previos.

 

 

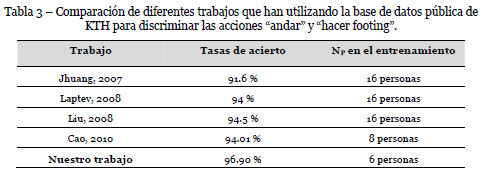
Nuestro método es capaz de distinguir entre las acciones de “andar” y “hacer footing” con un porcentaje de acierto del 96.90%, incluyendo simplemente 6 personas en el entrenamiento. La mayoría de trabajos previos habían utilizado 16 personas para obtener buenos resultados.

 

5. Conclusiones

Este artículo describe y presenta los resultados de la validación de una técnica denominada MVFI con diferentes bases de datos de vídeo. En concreto se ha utilizado una base de datos de vídeo propia (MILE-Human) y una base de datos pública muy utilizada en visión artificial (KTH-Human). Nuestro sistema es capaz de distinguir acciones humanas complejas como son “andar” y “hacer footing” sobre múltiples vídeos grabados en diferentes situaciones, cumpliendo la única característica de que la cámara sea estática. En futuros trabajos, se considerarán diferentes ángulos de cámara y distancias.

La técnica MVFI que hemos desarrollado, aunque es innovadora, está basada en métodos existentes, como el flujo óptico. Hemos demostrado que MVFI es capaz de detectar acciones humanas caracterizadas por cambios de velocidad. Por lo tanto, este trabajo sugiere la importancia de preservar la información de velocidad en cada secuencia de imágenes si deseamos utilizar técnicas de transformaciones canónicas para discriminar actividades humanas.

La ventaja de este sistema frente a otros existentes en la actualidad es la capacidad de clasificar acciones humanas en tiempo real, una vez que se ha realizado el entrenamiento, para ello se realizaron pruebas en un ordenador personal típico (Intel Core 2 Duo E8400 3.00GHz, 4 Gb RAM) obteniendo excelentes resultados. El proceso de coger una nueva secuencia de vídeo, transformarla con la plantilla de movimiento MVFI y proyectarla en el espacio canónico creado en el entrenamiento se puede realizar en tiempo real. Una de las aplicaciones en las que pensamos utilizar esta metodología es la segmentación automática de secuencias de vídeo, en función de los tipos de acciones realizadas.

Una futura línea de investigación en la que estamos trabajando, es la búsqueda y recuperación de vídeos basándose en contenido. El usuario podrá grabar un vídeo y nuestro algoritmo será capaz de obtener en una base de datos todos los vídeos con movimientos y acciones similares a los que esa persona ha realizado. El análisis se realizará con nuestra técnica de reconocimiento de acciones MVFI combinada con un algoritmo de seguimiento.

 

Referencias bibliográficas

Bobick, A. F., Davis, J. W. (2001). The recognition of human movement using temporal templates. IEEE Transactions on Pattern Analysis and Machine Intelligence, 23(3), 257-267.         [ Links ]

Boser, B. E., Guyon, I. M., Vapnik, V.Ñ. (1992). A training algorithm for optimal margin classifiers. In Proceedings of the 5th Annual ACM Workshop on Computational Learning Theory, 144-152.         [ Links ]

Bradski, A. (2008). Learning OpenCV, Computer Vision with OpenCV Library. O’Reilly Media, 1. edition.         [ Links ]

Cao, L., Liu, Z., Huang, T. (2010). Cross-dataset action detection. In Computer Vision and Pattern Recognition, 2010. CVPR 2010.         [ Links ]

Cho, Ch. W., Chao, W. H., Lin, S. H., Chen, Y. Y. (2009) A vision-based analysis system for gait recognition in patients with parkinson's disease. Expert Systems with Applications, 36(3), 7033-7039.         [ Links ]

Das, S. R., Wilson, R. C., Lazarewicz, M. T., Finkel, L. H. (2006) Two-stage PCA extracts spatiotemporal features for gait recognition. Journal of Multimedia, 1(5), 9-17.         [ Links ]

Deutscher, J., Reid, I. (2005). Articulated body motion capture by stochastic search. Int. J. Computer Vision, 61(2), 185-205.         [ Links ]

Etemad, K., Chellappa, R. (1997). Discriminant analysis for recognition of human face images. In Proceedings of the First International Conference on Audio- and Video-Based Biometric Person Authentication, AVBPA '97, 127-142.         [ Links ]

Farnebäck, G. (2003). Two-frame motion estimation based on polynomial expansion. In Proceedings of the 13th Scandinavian Conf. on Image Analysis, 363-370, 2003.         [ Links ]

Forsyth, D. A., Arikan, O., Ikemoto, L., O’Brien, J., Ramanan, D. (2006) Computational studies of human motion: Part 1, tracking and motion synthesis. Foundations and Trends in Computer Graphics and Vision, 1(2/3):77-254.         [ Links ]

Fukunaga, K. (1990). Introduction to statistical pattern recognition (2nd ed.). Academic Press Professional, Inc., San Diego, CA, USA        [ Links ]

Gonzalez, R. C., Woods, R. E., Eddins, S. L. (2003). Digital Image Processing Using MATLAB. Prentice-Hall, Inc., Upper Saddle River, NJ, USA.         [ Links ]

Huang, P. S., Harris, C. J., Nixon, M. S. (1999). Recognising humans by gait via parametric canonical space. Artificial Intelligence in Engineering, 13(4), 359-366.         [ Links ]

Ikizler, N., Forsyth, D. A. (2008) Searching for complex human activities with no visual examples. Int. J. Computer Vision, 80(3), 337-357.         [ Links ]

Jhuang, H., Serre, T., Wolf, L., Poggio, T. (2007). A biologically inspired system for action recognition. In Computer Vision, 2007. ICCV 2007. IEEE 11th International Conference on, 1-8.         [ Links ]

Laptev, I., Marszalek, M., Schmid, C., Rozenfeld, B. (2008). Learning realistic human actions from movies. In 2008 IEEE Conference on Computer Vision and Pattern Recognition, 1-8.         [ Links ]

Liu, J., Shah, M. (2008). Learning human actions via information maximization. In Computer Vision and Pattern Recognition, 2008. CVPR 2008. IEEE Conference on, 1-8.         [ Links ]

Meeds, E. W., Ross, D.A., Zemel, R.S., Roweis S.T. (2008) Learning stick-figure models using nonparametric bayesian priors over trees. In Proceedings of the EEE Conference on Computer Vision and Pattern Recognition (CVPR), 1-8.         [ Links ]

MILE (2011). Demos de MVFI en la Web de nuestro grupo de investigación. Disponible en: http://www.milegroup.net/demos        [ Links ]

Olivieri D.N., Gómez Conde, I., Vila, X.A (2011). Eigenspace-based fall detection and activity recognition from motion templates and machine learning. Expert Systems with Applications, doi:10.1016/j.eswa.2011.11.109.         [ Links ]

Poppe, R. (2010). A survey on vision-based human action recognition. Image & Vision Computing, 28(6), 976-990.         [ Links ]

Theodoridis, S., Pikrakis, A., Koutroumbas, K., Cavouras, D. (2010) Introduction to Pattern Recognition : A Matlab Approach. Elsevier Inc.         [ Links ]

Vapnik, V. Ñ. (1995). The nature of statistical learning theory. Springer-Verlag New York, Inc., New York, USA.         [ Links ]

 

Recebido/Recibido: 13/07/2011

Aceitação/Aceptación: 09/12/2011