Sistema de Apoio à Decisão para o Transporte Não Urgente de Doentes em Veículo Partilhado

Decision Support System for Not Urgent Transportation of Patients in Shared Vehicle

 

José António Oliveira¹, João Ferreira¹, Manuel Figueiredo¹, Luis Dias¹, Guilherme Pereira¹

¹ Centro de Investigação ALGORITMI, Escola de Engenharia – Universidade do Minho, Escola de Engenharia – Universidade do Minho, Campus Azurém, 4800-058 Guimarães, Portugal (Jose.Oliveira@algoritmi.uminho.pt,joao.aoferreira@gmail.com, Manuel.Figueiredo@algoritmi.uminho.pt,Luis.Dias@algoritmi.uminho.ptLuis.Dias@algoritmi.uminho.pt, Guilherme.Pereira@algoritmi.uminho.pt)

 

RESUMO

O transporte não urgente de doentes em Portugal foi alvo de reformulação legislativa de modo a reduzir os custos que acarretava. Neste artigo apresentam-se métodos heurísticos para a formação de agrupamentos de doentes a serem transportados na mesma viatura. São apresentados resultados computacionais que validam os algoritmos desenvolvidos. Os algoritmos podem ser facilmente integrados num sistema de apoio à decisão.

Palavras-chave: Algoritmo Genético; Problema de Roteamento de Veículos; Transporte a Pedido; Problemas da Orientação de Equipas; Transporte Não Urgente de Doentes.

 

ABSTRACT

The non-emergency patient transport service in Portugal was targeted by legislative reforms aiming to reduce costs. This paper presents heuristic methods for grouping patients to be transported in the same vehicle. The computational results are presented and validate the developed algorithms. These algorithms can be easily integrated into a decision support system.

Keywords: Genetic Algorithm; Vehicle Routing Problem; Dial-a-Ride Problem; Team Orienteering Problem; Non-emergency Patient Transport Service.

 

1. Introdução

Em 2012, Portugal publicou em Diário da Republica (DRE) vários documentos sobre o transporte não urgente de doentes (TNUD). A motivação legislativa teve por base um imperativo previsto no Memorando de Entendimento assinado entre o Governo Português e o Fundo Monetário Internacional, o Banco Central Europeu e a União Europeia, que estabeleceu ser necessário efectivar com urgência a concretização de medidas operacionais efetivas que reduzissem o custo de TNUD.

Em 2011, a Administração Regional de Saúde do Norte (ARSN, 2011) referiu a implementação de um sistema informático com o objectivo de optimizar a gestão do TNUD. Pode ler-se no documento publicado que o sistema informático “vai permitir um maior rigor ao nível da prescrição e, simultaneamente, assegura a sua organização de forma racional, promovendo o transporte múltiplo de utentes sempre que tal se justifique e seja possível.” A ARSN esperava alcançar uma redução dos custos de transportes na ordem dos 3.000.000€ referente a uma redução de 20% dos custos.

O Ministério da Saúde (DRE, 2011) mandatou a um grupo de trabalho a responsabilidade de estudar, analisar e propor medidas no âmbito do TNUD. O grupo de trabalho apresentou um relatório com um conjunto de orientações, algumas das quais vieram a ser objeto de publicação em Diário da República.

O regime de TNUD encontra-se definido pelas Portarias n.º 142-A/2012 (DRE, 2012a) e n.º 142-B/2012 (DRE, 2012b) e pelos Despachos n.º 7702-A/2012 (DRE, 2012e), e n.º 7702-C/2012 (DRE, 2012f). Foi necessário publicar legislação adicional de forma a rever alguns pontos particulares (DRE, 2012c; DRE, 2012d; DRE, 2012g; DRE 2012h). Adicionalmente, encontra-se legislado os valores de custo de transporte a ser suportado pelo Serviço Nacional de Saúde (SNS), no caso dos utentes com insuficiência económica (DRE, 2012e; DRE, 2012f).

 

2. Enquadramento do Problema Real

Nesta secção apresenta-se o problema real, descrevendo questões importantes que resultam da leitura da legislação.

2.1. Definição de Transporte Não Urgente de Doentes

À luz da legislação em vigor em 2014 em Portugal (DRE, 2012b), e no que diz respeito ao acesso às prestações do Serviço Nacional de Saúde (SNS), por parte dos utentes, considera-se TNUD o transporte associado à realização de uma prestação de saúde e cuja origem ou destino sejam os estabelecimentos e serviços que integram o SNS ou as entidades de natureza privada ou social com acordo, contrato ou convenção para a prestação de cuidados de saúde, nas seguintes condições: Consultas, internamento ou cirurgia de ambulatório; Tratamentos ou exames complementares de diagnóstico e terapêutica; Transporte do doente após a alta de internamento, com prévia prescrição médica; Transporte do doente após a alta de urgência, com prévia prescrição médica.

2.2. Prescrição do Transporte

A prescrição do transporte é da exclusiva competência do médico assistente, que deve obrigatoriamente registar os seguintes elementos no sistema de apoio ao médico (SAM) ou sistema equivalente: A justificação clínica, devidamente fundamentada, da necessidade de transporte; A verificação da condição económica; Nos casos em que haja necessidade de efetuar o transporte em ambulância: i) A justificação da modalidade de transporte; ii) As condições em que o transporte deve ocorrer, nomeadamente se o doente necessita de ventilação, oxigénio, monitorização, cadeira de rodas ou se trate de doente acamado ou isolado; A justificação da necessidade de acompanhante; A justificação da necessidade de acompanhamento de profissional de saúde. Após prescrição do transporte pelo médico, os serviços administrativos da entidade requisitante validam a condição económica do doente e procedem à requisição do transporte.

A requisição do transporte obedece aos critérios de minimização da distância entre o local de origem, que deve corresponder à morada a partir da qual o transporte é efetuado, e o local de destino, que deve ter em conta a localidade mais próxima do local de origem. O TNUD é realizado em ambulância ou em veículo de transporte simples de doentes (VTSD), que é um veículo ligeiro de passageiros, com lotação máxima de 9 lugares, destinado ao TNUD, cuja situação clínica não impõe a necessidade de cuidados de saúde durante o transporte.

O transporte não urgente de doentes é realizado, sempre que possível, em VTSD, tendo em consideração a necessidade de otimização da capacidade do veículo à luz dos seguintes critérios: a) Agrupamento de utentes que independentemente da origem se inserem no mesmo percurso; b) Destinados a estabelecimento de saúde preferencialmente no mesmo concelho e ou área geográfica; c) Utentes para o mesmo período horário de consulta ou tratamento.

O recurso a ambulâncias de transporte individual deve ser justificado, de forma fundamentada, pelo médico assistente. Para efeitos da realização do agrupamento de utentes admitem-se desvios ao percurso iguais ou inferiores a 10 km ou 30 minutos. Esclarece a Administração Central do Sistema de Saúde ( ACSS, 2014) que poderá acontecer um transporte em VTSD ser efetuado apenas com um doente em virtude de não se verificar a necessidade de transportar mais doentes no mesmo período e trajeto, factos impeditivos do agrupamento de doentes.

2.3. Organização do Transporte

Cabe à entidade requisitante a organização do transporte e a sua valorização de acordo com critérios de racionalidade económica obedecendo ao princípio de agrupamento de doentes transportados em função da otimização do percurso, dos estabelecimentos de destino e dos horários da prestação.

A requisição de transporte é efetuada por via informática através da aplicação de gestão integrada de transporte (AGIT), com base na informação inicial gerada no SAM. A requisição deve ser disponibilizada ao transportador através da AGIT, antes da realização do transporte. A requisição deve ainda ser disponibilizada à entidade prestadora dos cuidados de saúde, através da AGIT. Para garantir a integridade da informação, deve existir uma interligação entre as diferentes aplicações informáticas, nomeadamente entre o SAM e a AGIT. A AGIT deve possibilitar o acesso da entidade requisitante, do transportador, da entidade prestadora de serviço e da entidade supervisora.

O transporte deve ser programado e requisitado com a antecedência mínima de 48 horas. Em situações pontuais e de natureza excecional, o prazo referido no número anterior pode não ser observado desde que devidamente autorizado e exista acordo entre a entidade requisitante e a transportadora. A hora limite de aceitação tácita de aprovação/autorização de requisições do transporte diária, no sistema informático, ocorre até às 15 horas e 30 minutos.

Os pedidos de transporte são agrupados tendo em conta os horários das prestações de cuidados às quais os doentes se destinam, de acordo com:

• a) Se o destino se situar, preferencialmente, dentro dos limites geográficos do concelho de origem dos doentes ou num raio não superior a 10 km, estes são agrupados com intervalos, entre a prestação do primeiro doente e a do último, de uma hora;
• b) Caso o destino se situe fora do concelho de origem dos doentes, o intervalo entre a prestação do primeiro doente e a do último pode ser de duas ou quatro horas, consoante o número de quilómetros a percorrer seja, respetivamente, inferior ou superior ao número de quilómetros a fixar por cada entidade responsável pela organização do transporte em função das suas caraterísticas geográficas, num intervalo de 100 km a 130 km.

A lei estabelece que na “0timização dos percursos” deve ser aplicada a regra do desvio máximo, ou seja, podendo ser agrupados os doentes, para um percurso e ao longo do mesmo, para além das freguesias e concelhos, desde que não exista um desvio superior a 10 km ou 30 minutos, inerente a cada recolha de doentes para o transporte único em apreço, sendo observados os limites referidos na alínea b) do parágrafo anterior.

2.4. Encargos do Transporte

Os encargos resultantes do TNUD são da responsabilidade da entidade requisitante. Deste modo torna-se importante para a entidade requisitante a otimização e racionalização do processo de transporte não urgente de doentes. Não se conhece o modo como a entidade requisitante deve fazer a otimização dos TNUD, pelo que se considera este estudo ser oportuno e um contributo importante.

2.5. Revisão de Literatura

Recentemente Díaz-Parra et al. (2014) publicaram uma revisão do estado da arte sobre o problema dos transportes que apresenta várias variantes de problemas, formulações matemáticas e técnicas utilizadas na solução dos problemas.

A área da saúde é fértil em problemas de gestão e organização que têm vindo a ser estudados ao longo das últimas décadas (Stiver et al. 1982, Begur, Miller e Weaver, 1997). O estudo deste tipo de problemas é crescente, e no mundo ocidental resulta do aumento da procura dos cuidados da saúde e da necessidade de se manter os custos sociais o mais baixo possível. O aumento da procura de cuidados de saúde tem dois vetores que justificam o seu crescimento: a democratização do acesso aos cuidados de saúde nas sociedades desenvolvidas e o envelhecimento da população.

O transporte na área da saúde é um assunto estudado na literatura de otimização de processos logísticos desde há muitos anos. Têm sido aplicados com sucesso na área da saúde os desenvolvimentos realizados na logística industrial, quer ao nível do transporte, quer da planificação, quer da informação. Hoje em dia, sistemas de informação dão apoio à tomada da decisão, permitindo obter ganhos de eficácia e de eficiência. Vaisblat e Albert (2013) efetuaram um estudo sobre o escalonamento de uma frota especial atendendo às necessidades dos pacientes. Hains et al. (2011) abordaram a questão da segurança e da qualidade no TNUD.

Um dos problemas mais estudados na Gestão Logística é o problema de roteamento de veículos (VRP – Vehicle Routing Problem), em que basicamente se pretende definir para um conjunto de viaturas as rotas de visita a locais bem definidos. Este problema apresenta um grande número de variantes, que abordam situações particulares ou mais específicas. Uma das variantes do VRP é o transporte de mercadorias (Berbeglia et al. 2010), em que se pode ter a situação de entrega e recolha de bens (PDP - Pickup and Delivery Problems). Em geral são uma classe dos problemas de roteamento de veículos em que os objetos (ou as pessoas) têm de ser transportados entre uma origem e um destino. Conforme apresenta Berbeglia et al. (2010), estes problemas podem ser classificados em três grupos quanto à origem e destino das mercadorias: o primeiro grupo é composto pelos problemas “muitas(origens)-para-muitos(destinos)”, em que qualquer vértice pode servir como uma fonte ou como um destino para qualquer mercadoria; no segundo temos a situação “uma(origem)-para-muitos(destinos)-para-um(destino) final”; e por fim no terceiro grupo temos a situação “uma(origem)-para-um(destino)”.

Os mesmos autores (Berbeglia et al. 2010) referem a natureza estática ou dinâmica deste tipo de problemas. No caso estático, toda a informação é conhecida antecipadamente e não se altera durante a fase da construção e implementação da solução. No caso dinâmico, a informação disponível é atualizada (alterada) à medida que se constrói ou se implementa parte da solução, por força de novos pedidos dos utilizadores. Nestes problemas, a solução proposta será uma estratégia de solução que pode também ser alterada com o decorrer do tempo. Tipicamente situações dinâmicas deste tipo ocorrem nos problemas de transporte a pedido de utentes com necessidades especiais, onde é enviado uma viatura ao local onde se encontram para serem transportados ao seu destino. A vertente dinâmica deste problema resulta do facto de os pedidos de transporte surgirem por vezes no mesmo dia em que necessitam de ser realizados: este tipo de problema designa-se por DARP (Dial-A-Ride Problem).

Ainda não existem muitos estudos sobre PDP dinâmicos, em particular nas variante dinâmica “uma(origem)-para-muitos(destinos)-para-um(destino) final”. Um dos problemas dinâmicos mais estudados designa-se por OlDARP (On-line Dial-A-Ride Problem) (Hauptmeier et al. 2000; Feuerstein e Stougie, 2001; Jaillet e Wagner, 2008). Este problema não apresenta as restrições adicionais que delimitam o desconforto do utilizador, tais como a duração máxima da viagem e a duração da janela temporal, conforme aparece no DARP dinâmico.

O DARP quer na versão estática ou dinâmica tem recebido importantes contributos, como por exemplo a revisão de Cordeau e Laporte (2007). O estudo com uma única rota para este problema foi realizado por Psaraftis (1988) onde os clientes solicitam um serviço a ser disponibilizado tão cedo quanto possível. Sempre que um novo pedido é introduzido, o sistema atualiza a instância e a partir da rota parcialmente realizada tenta acomodar o novo pedido na rota que falta concretizar. Por seu lado, Madsen et al. (1995) apresentaram um algoritmo para um caso real do DARP dinâmico com múltiplos veículos que atendia até 300 pedidos diários para o transporte de pessoas com necessidades especiais.

 

3. O Modelo

O problema real que é estudado neste artigo diz respeito ao transporte não urgente de doentes de suas casas para o hospital e do hospital para suas casas. Atualmente em Portugal o serviço de transporte funciona na modalidade em que os doentes são recolhidos em suas casas para tratamento hospitalar e novamente transportados para suas casas. Configura-se a situação -“muitas(origens)-para-um(destino)-para-muitos(destinos)”. Está inclusive previsto o pagamento do tempo de espera que a viatura faz junto ao hospital pelos doentes que transportou. A forma como se organiza o transporte não está claramente estabelecida na legislação.

3.1. Comparação de Estratégias de Transporte

Considere-se o seguinte exemplo numérico para ilustração do problema real, apresentado na Figura 1, onde são apresentados 4 vértices (O, A, B e C), em que O representa a origem onde se encontra a viatura que para efeitos de simplificação considera-se ser também o hospital. Os vértices A, B e C representam a localização das pessoas a serem transportadas para o hospital. A Figura 1 apresenta uma solução que utiliza 3 viaturas, significando o transporte mais cómodo, mais rápido e mais flexível dos doentes. Qualquer outra situação não será tão cómoda para os utentes. Pode-se assumir que esta solução irá representar o limite máximo a pagar pela unidade hospitalar.

 

 

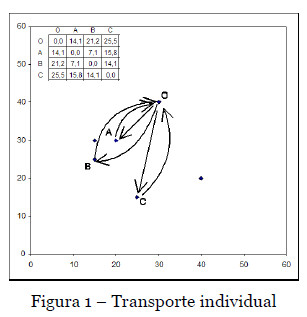
Considerando a tabela de distâncias (euclidianas) representada na Figura 1, a distância total percorrida pelas três viaturas (com origem e regresso a O) é 121,6 unidades ((14,1+21,2+25,5)*2). As 13 possibilidades de se fazer o transporte deste pequeno exemplo com diferentes números de viaturas é mostrado na Tabela 1, em que as cores representam diferentes viaturas.

 

 

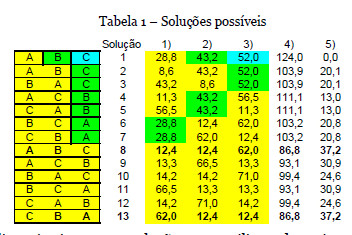
A solução 1 utiliza três viaturas, as soluções 2 a 7 utilizam duas viaturas, e as restantes soluções utilizam uma viatura. A solução 5 estabelece a rota O-C-A-O para uma viatura e a rota O-B-O para a outra viatura. A solução 1 é a solução em que cada utente faz um transporte individual e por esse motivo cada utente viaja a menor distância possível, conforme é ilustrado na Figura 1. As colunas 1), 2) e 3) estabelecem o custo total do transporte, para os vértices A, B e C, de acordo com a legislação, refletindo já a viagem de casa do utente para o hospital e regresso a casa. No caso do transporte individual da solução 1, para cada utente é aplicado o custo de 0,51€ por km. Em concreto para o utente em A, o custo de transporte é 28,8 (=14,1*4*0,51). Nos casos de agrupament0, segundo a lei, o utente mais distante é designado de “primeiro doente” e é aplicado esta forma de cálculo. Para os restantes utentes que são incluídos no mesmo transporte, é cobrado 20% do valor cobrado pelo “primeiro utente”. A coluna 4) apresenta a soma dos custos 1)…3). O menor valor da soma dos custos foi obtido na solução 8 e na solução 13. A coluna 5) apresenta a diferença do custo de cada solução para a solução 1 que é a solução mais confortável para os utentes. A coluna 5) pode ser usada como uma função objetivo deste problema onde se pretende maximizar a poupança dos custos de transporte relativamente à solução do transporte individual. Esta função objetivo identifica a solução 8 e a solução 13 como sendo as melhores soluções. A Figura 2 apresenta a solução 8 e a solução 13. Nestas soluções utiliza-se uma única viatura. Na solução 8 o utente transportado do vértice C é o último a ser recolhido, enquanto que na solução 13 o utente C é o primeiro a ser recolhido, e à luz da legislação configura-se como sendo o doente mais distante do hospital. No espírito da Lei, a solução 8 não pode ser considerada, porque pretende-se encontrar soluções onde se minimiza para cada utente a distância percorrida até ao hospital.

 

 

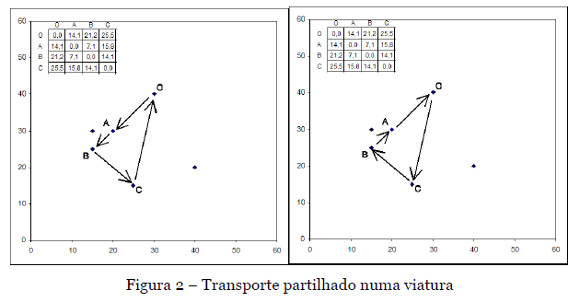
Para se verificar se a solução 13 é uma solução que cumpre as restrições sobre os desvios permitidos pela lei, referidos na Secção 2.2, calcula-se o aumento da viagem para o utente C, dado que os utentes A e B não têm aumento de distância face à solução de transporte individual. O percurso C-B-A-O tem uma distância 35,3 (=14,1+7,1+14,1) enquanto o percurso C-O tem uma distância 25,5. Verifica-se um aumento de 9,8 que é inferior ao limite de 10 imposto pela lei, o que valida a solução. Considera-se nesta exemplificação que em termos de velocidade é efetuada 60km/h o que significa o mesmo valor das unidades da distância percorrida. Porém, se a viatura se deslocar a uma velocidade média inferior a 19,6 km/h demoraria mais de 30 minutos, partindo de C, a efetuar o desvio para recolher os utentes B e A, o que tornaria a solução não admissível. A solução 8 é não admissível devido à não verificação do desvio máximo permitido para o doente A, senão vejamos: o trajeto de A-O igual a 14,1 passaria para 46,7 A-B-C-O.

Existem ainda restrições adicionais relativamente aos tempos de espera que os utentes A, B e C terão acrescidos pelo facto de esperarem pelo último utente a ser consultado; e relativamente ao tempo de início das consultas de cada um dos utentes. A conceção de um algoritmo construtivo para o agrupamento de doentes para a realização de TNUD múltiplo tem de ser incorporado num sistema de informação capaz de obter informação registada no AGIT de modo a verificar todas as restrições impostas pela lei.

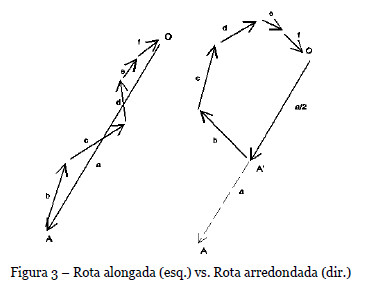
O espírito do legislador visava o agrupamento para rotas alongadas, que ao invés não permite a elaboração de rotas mais arredondadas. A Figura 3 ilustra duas rotas, em que a rota arredondada mesmo tendo um comprimento menor, não é aceite devido ao não cumprimento do desvio máximo permitido.

 

 

3.2. O Modelo TOP

O Problema de Orientação de Equipas (TOP - Team Orienteering Problem) é um problema de encaminhamento de viaturas do âmbito do VRP. Este problema é relativamente recente e tem recebido uma significativa atenção por parte da comunidade científica (Vansteenwegen, Souffriau, Oudheusden, 2011; Archetti, Speranza e Vigo, 2013) , quer apresentando metodologia de solução exata (Archetti, Bianchessi e Speranza, 2013), quer metodologia de solução aproximada (Hu e Lim, 2014). Vansteenwegen e a sua equipa mantêm um repositório de instâncias públicas (The Orienteering Problem: Test Instances, 2014).

A principal diferença entre o TOP e o VRP está relacionada com o facto de no TOP nem todos os vértices do grafo (clientes) terão de ser visitados, tal como acontece no VRP. No TOP poderão não ser atendidos alguns dos clientes. Em vez de se usar o modelo baseado no problema VRP decidiu-se modelar pelo formato do TOP. O que irá acontecer é que dada uma lista de doentes não urgentes para os quais foi solicitado transporte e dada uma frota de viaturas disponível com lotação de oito lugares, faz-se a atribuição de serviços de transporte de modo a maximizar a ocupação da viatura e minimizar a distância percorrida. Os doentes que não podem ser integrados nas rotas destas viaturas serão transportados em ambulâncias especialmente requisitadas para este serviço.

Gutiérrez-Jarpa et al. (2009) estudaram o problema com entregas fixas e recolhas opcionais, tornando este problema uma situação mista de VRP para a entrega e TOP para a recolha. Os autores estudaram o caso particular de uma única viatura e apresentaram um novo método branch-and-cut que permite resolver instâncias maiores. Apesar do grande interesse prático que esta modelação tem para a logística inversa, os autores referem terem encontrado somente o trabalho de Gribkovskaia et al. (2008), que também só considera uma única viatura. A nova formulação proposta permitiu solucionar instâncias ainda em aberto e por outro lado reduziu significativamente o tempo de solução. O método consegue resolver instâncias até 90 vértices. Os autores referem a necessidade de se estender a investigação aos casos com múltiplos veículos e o desenvolvimento de heurísticas para a solução de instâncias de grandes dimensão.

Dado que o agrupamento de doentes é uma situação fortemente restringida, é nossa opção modelar o problema real apresentado pelo SNS como uma resolução de um problema TOP, para o conjunto de viaturas disponíveis. Os vértices não incluídos nas rotas do problema TOP serão os utentes que farão o trajeto em transporte individual.

 

4. Metodologia Desenvolvida

4.1. O Algoritmo Construtivo

É possível definir-se um método para a construção das rotas do tipo algoritmo de inserção de menor custo, com vista à elaboração de rotas válidas. A Figura 4 ilustra um algoritmo construtivo para a geração de rotas.

 

 

Considere-se o exemplo numérico da Tabela 2 com oito utentes, em que o vértice O representa o hospital. Por simplicidade considera-se que as viaturas estão localizadas em O (depósito)

 

 

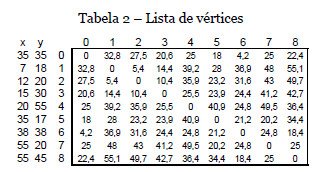
Seguindo o Algoritmo Construtivo, o vértice mais distante do depósito é o vértice 1. A distância da rota O-1-O é 65,6. O limite máximo permitido é uma rota de 75,6 (=65,6+10). O próximo vértice a ser testado é o vértice 2, que verifica a condição de distância. A rota parcial O-1-2-O tem comprimento 65,7. O próximo vértice a ser testado é o vértice 3. A inclusão é válida e a rota O-1-2-3-O tem cumprimento 69,2. O próximo vértice a ser testado é o vértice 4 mas a rota O-1-2-3-4-O tem distância 99,1 o que não é admissível. Nenhum dos restantes vértices pode ser adicionado, e a rota é fechada.

A aplicação do algoritmo produz a solução representada na Figura 5. A solução utiliza cinco viaturas, das quais três transportam um único utente. Foi possível agrupar três utentes numa viatura e agrupar dois utentes noutra viatura.

 

 

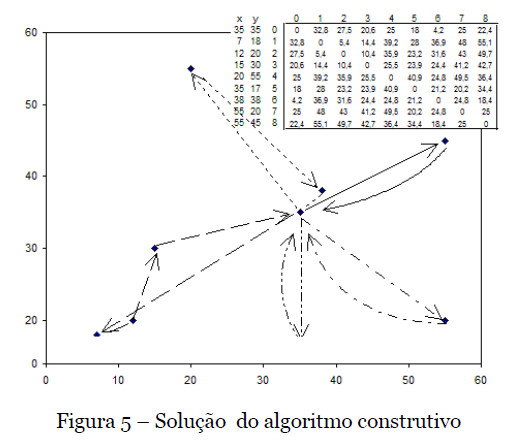
Um algoritmo construtivo elabora soluções rapidamente. Porém a qualidade das soluções pode ser muito baixa em termos de função objetivo. De modo a melhorar a qualidade das soluções pode ser usado um método de pesquisa local ou meta-heurística como por exemplo um algoritmo genético.

4.2. O Algoritmo Genético

O algoritmo genético (GA) é uma heurística de pesquisa que imita o processo da evolução das espécies. Este método utiliza técnicas inspiradas na natureza, tais como mutação, cruzamento, herança e seleção, para gerar soluções para problemas de otimização. O sucesso de um GA depende do tipo e da complexidade do problema ao qual ele é aplicado, embora, no nosso entender, seja o método mais apto a ser aplicado em problemas onde se tem pouco conhecimento específico do problema. Gavalas et al. (2014) apresentam uma revisão sobre modelos e abordagens de solução (GA inluídos) a um conjunto de problemas de roteamento.

4.2.1. O Cromossoma

Na ferramenta desenvolvida e apresentada neste trabalho, ao aplicar os conceitos de um algoritmo genético para modelar um TOP dedicado ao problema TNUD, assumiu-se que: há um conjunto de n pontos de recolha que devem ser visitados, no máximo, uma vez e por um único veículo; cada ponto de recolha é representado por um vértice num grafo; A frota de m veículos está disponível num depósito; o depósito é representado por um vértice num grafo.

Num GA os cromossomas ou indivíduos são representados como cadeias de carateres que codificam soluções candidatas para um problema de otimização, que vão evoluindo para melhores soluções. No TOP, um cromossoma pode ser composto por n genes, ou seja, um gene para cada vértice. Decidimos definir um cromossoma formado por n genes, em que cada gene define a prioridade do vértice para ser seleccionado para ser visitado. Esta estrutura foi adaptada do modelo de Chaves Aleatórias (Random Keys) apresentado por Morán-Mirabal et al. (2014).

4.2.2. Os Genes

Um cromossoma codifica uma solução possível, que no caso do TOP corresponde a um conjunto de m rotas válidas; cada gene representa um ponto de recolha e está associado ao vértice respectivo do grafo; um gene tem associado um alelo que corresponde à prioridade do ponto de recolha em ser visitado.

O gene i do cromossoma corresponde ao vértice i no grafo. O alelo (valor ou informação contida no gene) identifica a prioridade do vértice. Nos nossos algoritmos, em vez da utilização de valores convencionais no intervalo [0, 1[ para os alelos dos genes (Morán-Mirabal et al., 2014), usamos valores inteiros no intervalo [0, n[. No estabelecimento dos valores iniciais dos genes, a distância do vértice ao depósito é utilizada como fator de prioridade, uma vez que vértices mais distantes geram maior desvio permitido para agrupar mais vértices.

4.2.3. Descodificador do Cromossoma

Para se obter uma solução do problema a partir de um cromossoma é necessário interpretar o vetor de chaves aleatórias, e tal é feito utilizando um descodificador do cromossoma. No nosso estudo, a associação de um cromossoma a uma solução para o TOP é feita pelo algoritmo construtivo apresentado, que constrói a solução pela leitura dos alelos presentes nos genes do cromossoma. Os valores dos alelos servirão para ordenar os vértices na lista Laux do Algoritmo Construtivo apresentado na Figura 4.

4.2.4. Avaliação das Soluções

A concepção de um GA requer uma representação genética do domínio das soluções, bem como uma função de aptidão para avaliar a qualidade das soluções produzidas. No que diz respeito ao TNUD, a função de aptidão do algoritmo genético desenvolvido corresponde à poupança que é possível obter pelo agrupamento de doentes face à solução de transporte individual.

4.2.5. Implementação

Uma aplicação de software JAVA foi desenvolvida para implementar o algoritmo genético com duas variantes ao nível do algoritmo construtivo, e designou-se por GATOP-1 GATOP-2. A aplicação tem uma simples, mas funcional, Interface Gráfica do Utilizador (GUI - Graphical User Interface), com um conjunto de opções que permite que os parâmetros do GA possam ser ajustados e ajudar a obter melhores resultados num problema ou instância específica do TOP. Há também um elemento de visualização (Solution Viewer), que ilustra o exemplo carregado e apresenta as rotas da melhor solução encontrada até ao momento, que são atualizadas em tempo real. Na Figura 6 apresenta-se o “Solution Viewer”, onde os círculos correspondem aos vértices no TOP e um screenshot da aplicação.

 

 

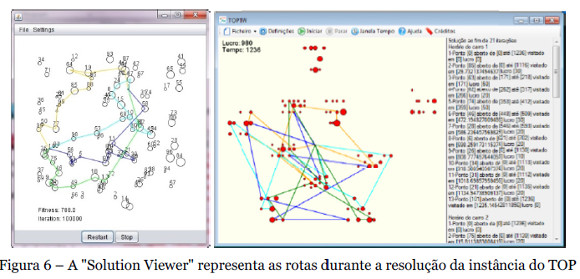
O algoritmo construtivo do GATOP-2 tem uma abordagem “mais paralela” na construção de rotas. As rotas vão sendo abertas e adicionados novos vértices de um modo simultâneo. O fecho das rotas ocorre no final do algoritmo construtivo. No caso do GATOP-1 uma rota é fechada antes da abertura da rota seguinte.

 

5. Resultados Computacionais

Realizaram-se uma série de testes computacionais com o intuito de avaliar a performance dos algoritmos apresentados, comprando os resultados obtidos entre eles e também com os valores do estado da arte. Para os testes utilizaram-se 24 instâncias públicas de teste para o TOP, selecionadas aleatoriamente de entre as 320 instâncias publicadas por Chao et al. (1996).

Os resultados obtidos nos testes com os dois algoritmos foram comparados com os melhores resultados encontrados na literatura relativa ao TOP. Os testes foram realizados com recurso a um computador laptop com processador Intel Pentium Core2Duo P8700 2.53 GHz 64-bit com 4 GB de memória RAM. Foram efetuadas dez execuções com cada um dos algoritmos em cada instância. Os resultados alcançados constam na Tabela 3, onde o valor na coluna (Avg) corresponde ao valor médio para cada instância após as dez execuções do algoritmo.

 

 

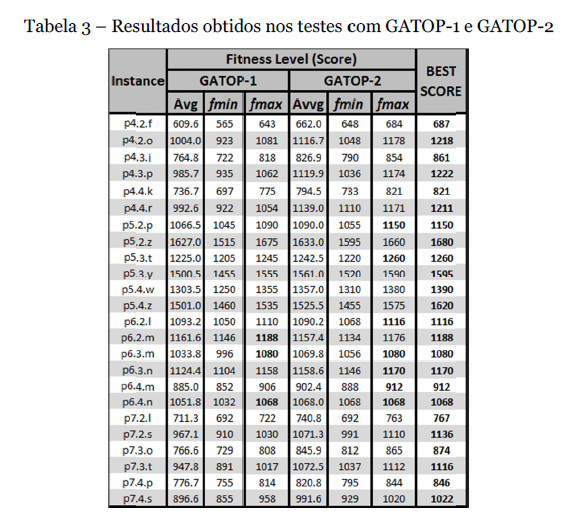
Os valores em (fmin) e (fmax) são respectivamente os valores mínimos e máximos obtidos para cada instância. Na coluna (BEST SCORE) constam os valores máximos atuais para cada instância e que constam na literatura. É de destacar a superior consistência do GATOP-2 face ao GATOP-1, pois existe em média uma menor diferença entre os valores (fmax) e (fmin). Em termos de exactidão, de novo o GATOP-2 mostrou-se superior ao obter uma diferença média de 0.9% em relação aos melhores valores conhecidos para cada instância (BEST SCORE). O algoritmo GATOP-2 conseguiu igualar os melhores resultados em 7 das 24 instâncias, enquanto que o GATOP-1 conseguiu igualar os melhores resultados apenas em 3 instâncias.

 

6. Conclusões

Ao longo deste artigo foram apresentadas duas ferramentas de software denominadas GATOP 1 e GATOP 2, as quais permitem resolver o problema de orientação de equipas (TOP - Team Orienteering Problem) aplicado ao TNUD através de algoritmos genéticos. Os dois algoritmos genéticos foram testados e analisados num conjunto de 24 instâncias públicas, tendo-se concluído que o desempenho médio do GATOP-2 é claramente melhor do que o de GATOP-1 quando comparados aos melhores valores conhecidos as mesmas instâncias.

No geral, as ferramentas desenvolvidas são intuitivas e de fácil utilização, e permitem resolver com sucesso o TOP. As ferramentas são facilmente integráveis num sistema de apoio à decisão para a organização do transporte não urgente de doentes. Como trabalho futuro pretendemos continuar o estudo do TOP e das suas variantes que consideram janelas temporais para os utentes em função da hora limite a que devem recolhidos para serem transportados até ao seu destino.

 

Agradecimento

Os autores expressam o seu agradecimento aos quatro revisores anónimos que, com os seus comentários, permitiram melhorar consideravelmente este artigo.

Este trabalho foi parcialmente financiado pelo projeto GATOP - Genetic Algorithms for Team Orienteering Problem (Ref PTDC/EME-GIN/ 120761/2010), financiado por fundos nacionais pela FCT / MCTES e co-financiado pelo European Social Development Fund (FEDER) através do COMPETE Programa Operacional Fatores de Competitividade (POFC) Ref FCOMP-01-0124-FEDER-020609.

 

Referências

ACSS (2014). Acessível em http://www.acss.min-saude.pt/

Archetti, C., Bianchessi, N., & Speranza, M. G. (2013). Optimal solutions for routing problems with profits. Discrete Applied Mathematics, 161(4), 547-557.         [ Links ]

Archetti, C., Speranza, M. G., & Vigo, D. (2013). Vehicle routing problems with profits. Tech. Report WPDEM2013/3, University of Brescia.         [ Links ]

ARSN (2011). http://portal.arsnorte.min-saude.pt/portal/page/portal/ARSNorte

Begur, S. V., Miller, D. M., & Weaver, J. R. (1997). An integrated spatial DSS for scheduling and routing home-health-care nurses. Interfaces, 27(4), 35-48.         [ Links ]

Berbeglia, G., Cordeau, J. F., & Laporte, G. (2010). Dynamic pickup and delivery problems. European Journal of Operational Research, 202(1), 8-15.         [ Links ]

Chao, I. M., Golden, B. and Wasil, E. A. (1996) Theory and Methodology - The Team Orienteering Problem. European J. of Op. Research,88, 464-474.         [ Links ]

Cordeau, J. F., & Laporte, G. (2007). The dial-a-ride problem: models and algorithms. Annals of Operations Research, 153(1), 29-46.         [ Links ]

Díaz-Parra, O., Ruiz-Vanoye, J. A., Bernábe Loranca, B., Fuentes-Penna, A., & Barrera-Cámara, R. A. (2014). A Survey of Transportation Problems. Journal of Applied Mathematics, vol. 2014, Article ID 848129, 17 pages, 2014. doi:10.1155/2014/848129        [ Links ]

DRE (2011). Despacho n.º 16843/2011, Diário da República, 2.ª série — N.º 239 — 15 de Dezembro de 2011, 48767-48768

DRE (2012a). Portaria n.º 142-A/2012. Diário da República, 1.ª série — N.º 94 — 15 de maio de 2012, 2532-(2)-2532-(3).

DRE (2012b). Portaria n.º 142-B/2012. Diário da República, 1.ª série — N.º 94 — 15 de maio de 2012, 2532-(3)-2532-(6)

DRE (2012c). Declaração de Retificação n.º 27-A/2012. Diário da República, 1.ª série — N.º 107 — 1 de junho de 2012, 2928-(2).

DRE (2012d). Portaria nº178-B/2012. Diário da República, 1.ª série — N.º 107 — 1 de junho de 2012, 2928-(2).

DRE (2012e). Despacho n.º 7702-A/2012. Diário da República, 2.ª série — N.º 108 — 4 de junho de 2012, 20410-(2).

DRE (2012f). Despacho n.º 7702-C/2012. Diário da República, 2.ª série — N.º 108 — 4 de junho de 2012, 20410-(3)-20410-(6).

DRE (2012g). Despacho nº 8705/2012. Diário da República, 2.ª série — N.º 125 — 29 de junho de 2012, 22880- 22881.

DRE (2012h). Declaração de Retificação n.º 36/2012. Diário da República, 1.ª série — N.º 135 — 13 de julho de 2012, 3657- 3664

Feuerstein, E., & Stougie, L. (2001). On-line single-server dial-a-ride problems. Theoretical Computer Science, 268(1), 91-105.         [ Links ]

Gavalas, D., Konstantopoulos, C., Mastakas, K., & Pantziou, G. (2014). A survey on algorithmic approaches for solving tourist trip design problems. Journal of Heuristics, 20(3), 291-328.         [ Links ]

Gribkovskaia, I., Laporte, G., & Shyshou, A. (2008). The single vehicle routing problem with deliveries and selective pickups. Computers & Operations Research, 35(9), 2908-2924.         [ Links ]

Gutiérrez-Jarpa, G., Marianov, V., & Obreque, C. (2009). A single vehicle routing problem with fixed delivery and optional collections. IIE Transactions, 41(12), 1067-1079.         [ Links ]

Hains, I. M., Marks, A., Georgiou, A., & Westbrook, J. I. (2011). Non-emergency patient transport: what are the quality and safety issues? A systematic review. International Journal for Quality in Health Care, 23(1), 68-75.         [ Links ]

Hauptmeier, D., Krumke, S. O., & Rambau, J. (2000). The online dial-a-ride problem under reasonable load (pp. 125-136). Springer Berlin Heidelberg.         [ Links ]

Hu, Q., & Lim, A. (2014). An iterative three-component heuristic for the team orienteering problem with time windows. European Journal of Operational Research, 232(2), 276-286.         [ Links ]

Jaillet, P., & Wagner, M. R. (2008). Online vehicle routing problems: A survey. In The Vehicle Routing Problem: Latest Advances and New Challenges (pp. 221-237). Springer US.         [ Links ]

Madsen, O. B., Ravn, H. F., & Rygaard, J. M. (1995). A heuristic algorithm for a dial-a-ride problem with time windows, multiple capacities, and multiple objectives. Annals of operations Research, 60(1), 193-208.         [ Links ]

Morán-Mirabal, L. F., González-Velarde, J. L., & Resende, M. G. C. (2014). Randomized heuristics for the family traveling salesperson problem. International Transactions in Operational Research, 21(1), 41-57.         [ Links ]

Psaraftis, H. N. (1988). Dynamic vehicle routing problems. Vehicle routing: Methods and studies, 16, 223-248.         [ Links ]

Stiver, H. G., Trosky, S. K., Cote, D. D., & Oruck, J. L. (1982). Self-administration of intravenous antibiotics: an efficient, cost-effective home care program. Canadian Medical Association Journal, 127(3), 207.         [ Links ]

The Orienteering Problem: Test Instances. http://www.mech.kuleuven.be/en/cib/op (29 maio 2014, último acesso)

Vaisblat, A., & Albert, D. (2013). Medical non-emergency patient centered scheduling solution. New Magenta Papers, 40.         [ Links ]

Vansteenwegen, P., Souffriau, W., & Oudheusden, D. V. (2011). The orienteering problem: A survey. European Journal of Operational Research, 209(1), 1-10.         [ Links ]

 

Recebido / Recibido: 12/04/2014

Aceitação / Aceptación: 06/06/2014