Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Similares em
SciELO
Similares em
SciELO
Compartilhar
RISTI - Revista Ibérica de Sistemas e Tecnologias de Informação
versão impressa ISSN 1646-9895
RISTI no.21 Porto mar. 2017
https://doi.org/10.17013/risti.21.67-84
ARTÍCULOS
Esquema de Visualización para Modelos de Clústeres en Minería de Datos
New Visualization Scheme for Cluster Models in Data Mining
Wilson Castillo-Rojas 1, Fernando Medina-Quispe 2, Juan Vega-Damke 2
1 Universidad de Atacama, Facultad de Ingeniería / DIICC, 1530000, Copiapó, Chile. wilson.castillo@uda.cl
2 Universidad Arturo Prat, Facultad de Ingeniería y Arquitectura, 1100000, Iquique, Chile. femedina@gmail.com
RESUMEN: El artículo propone el diseño e implementación de un esquema de visualización para modelos de clústeres, en el contexto de un proceso de minería de datos. En general, un buen modelo de clústeres no es difícil de interpretar, pero se torna compleja su representación visual cuando el conjunto de datos es de alto volumen, densidad y dimensionalidad. En este tipo de caso, es necesario contar con un apropiado esquema de visualización. El esquema visual que se propone en este trabajo se denomina VIMC, y se basa en cuatro características: visualización interactiva, combinación de técnicas de minería de datos, artefactos gráficos ad-hoc, y uso de métricas. Las métricas consideradas permiten comparar componentes de distintos clústeres, lo que a su vez ayuda a entender la composición de los grupos. A través de la implementación de un entorno visual web, y una evaluación de 23 usuarios, se logran resultados positivos sobre la utilidad de este esquema de visualización.
Palabras-clave: Visualización de clústeres, visualización de modelos para minería de datos, visualización de minería de datos, visualización interactiva de modelos, esquemas de visualización de datos.
ABSTRACT: The article proposes the design and implementation of a visualization scheme for cluster models, in the context of a data-mining process. In general, a good cluster model is not difficult to interpret, but its visual representation becomes complex when the data set is of high volume, density and dimensionality. In this type of case, it’s necessary to have an appropriate visualization scheme. The visual schema proposed in this work is called VIMC, and is based on four characteristics: interactive visualization, data-mining techniques combination, ad-hoc graphic artifacts, and use of metrics. The considered metrics allow to compare components of different clusters, which in turn helps to understand the composition of the groups. Through the implementation of a visual web environment, and an evaluation of 23 users, positive results are achieved on the utility of this visualization scheme.
Keywords: Cluster Visualization, model visualization for data mining, data mining visualization, interactive visualization of models, data visualization schemes.
1. Introducción
La comprensión e interpretación apropiada de los resultados de un modelo es el mayor problema o desafío en un proceso de Minería de Datos (MD). Algunas investigaciones sostienen que una de las formas de apoyar esta problemática es utilizando visualización en la etapa de construcción del modelo, y no solamente en el análisis exploratorio de los datos (entrada), y los patrones o reglas obtenidas en un proceso de MD (salida) (Meneses & Grinstein, 2001; Faria et al., 2015).
Lo anterior, afirma que al conocer el funcionamiento interno de un modelo permite, por un lado, comprender como funciona, y por otro lado interpretar mejor sus resultados. En particular, visualización de modelos de clústeres no es difícil de interpretar si el número de clústeres es relativamente manejable y son muy compactos. Sin embargo, cuando el conjunto de datos es de gran volumen, y el número de dimensiones es alto, su representación visual e interpretación se tornan complejos. Por ejemplo, con 3 dimensiones no se pueden observar todos los atributos simultáneamente, más en el caso de clústeres con alta densidad.
Como resultado del análisis comparativo de trabajos relacionados, y la evaluación de herramientas de MD existentes, se pudo constatar la dificultad que presenta la visualización de modelos de clústeres. También se confirma en esta revisión, que existen diversas métricas para comparar clústeres, y que la mayoría de las herramientas utilizan solamente el cálculo de distancia, y muy pocas, implementan comparación de componentes. Además, en ninguno de los trabajos y herramientas analizados utilizan combinación de técnicas de MD, y que proporcionan un bajo nivel de interacción, lo cual no permite explorar en profundidad un modelo.
En este contexto, este trabajo de investigación aborda el problema de la complejidad para visualizar modelos de clústeres con conjuntos de datos que reúnen las características antes mencionadas. Para esto, considera elementos en el diseño y desarrollo de un esquema de visualización, que permitan recorrer y explorar un modelo de clústeres, y mecanismos de interacción apropiados para lograr adentrarse en las componentes o instancias de cada clúster.
Una característica importante que se considera en este esquema visual, es la combinación de la técnica de clústeres con una técnica de MD del tipo descriptiva, que provea una vista complementaria de cada clúster, y de modo que permita establecer relaciones entre los atributos del conjunto de instancias agrupadas en cada uno. También, plantea necesario disponer de gráficos ad-hoc para representar visualmente clústeres, particularmente en conjuntos de datos con alto volumen, densidad y dimensionalidad. Otra característica fundamental es disponer de métricas que permitan comparar cuantitativamente instancias o componentes de un mismo clúster y entre distintos clústeres, y también medir el nivel de compacidad o dispersión de cada conglomerado.
El artículo describe la propuesta de un esquema de visualización para modelos de clústeres denominado VIMC. Se presenta su diseño conceptual y aspectos técnicos, además de la implementación de un entorno visual web, que proporciona las características principales de este esquema VIMC, estos son: visualización interactiva, combinación de técnicas de MD, gráficas vinculadas, métricas para comparar clústeres e instancias de los clústeres. Finalmente, se discute el resultado de una evaluación subjetiva obtenida a través de una encuesta en línea con 23 usuarios, todos con experiencia en procesos de MD.
2. Visualización en MD
El proceso de MD busca obtener a partir de un conjunto de datos, modelos de datos para describirlos o predecir nuevas instancias. Este proceso involucra etapas de: preparación de datos (entrada), generación del modelo (proceso), y la interpretación de patrones resultantes (salida). Esta salida debe significar un nuevo conocimiento en la organización, útil y comprensible para los usuarios finales, y que se puede integrar a los procesos para apoyar la toma de decisiones (Witten & Frank, 2005). Sin embargo, la dificultad está en identificar modelos en los datos, lo cual es una tarea compleja y, a menudo requiere experiencia, no sólo del analista de datos, sino también del experto en el dominio del problema.
El uso de capacidades de percepción visual humana, que puede detectar patrones fácilmente, puede ser útil para apoyar el análisis de modelos de MD. Bajo este enfoque, visualización en MD ha sido utilizada mayormente en el análisis exploratorio de datos (entrada), y presentación de los patrones (salida), dejando limitado este paradigma para el análisis de modelos (Meneses & Grinstein, 2001).
Un factor clave en MD, para mejorar la capacidad predictiva o descriptiva de un modelo, es entender cómo el modelo inducido está trabajando. Entre otros aspectos, por ejemplo; es importante entender cómo el modelo realiza una distribución del conjunto de datos de acuerdo a diferentes atributos, cómo las componentes del modelo están correlacionadas con un subconjunto de observaciones, y cómo el valor de los atributos es particionado por el modelo.
Algunas técnicas de aprendizaje automático funcionan como sistemas cerrados, y es difícil lograr una interpretación de los patrones obtenidos, y responder preguntas del usuario acerca de la transformación que realiza el modelo. Un ejemplo son las redes neuronales artificiales, que convergen a un conjunto de pesos numéricos que no tienen una interpretación directa en el dominio del problema.
Las técnicas como árboles de decisión son fácilmente comprensibles cuando el modelo es pequeño, árboles de mayor tamaño (más de 3 niveles) su interpretación es compleja. Lo mismo ocurre para un modelo de clústeres, ya que con datos de gran volumen y alta dimensionalidad, no es simple visualizar todos los atributos. Otras técnicas de aprendizaje como reglas de asociación, también el tamaño del modelo presenta problemas (largas listas de reglas), y requiere el desarrollo de nuevas representaciones gráficas, que proporcionen una mejor visualización e interacción con el modelo, para facilitar su interpretación. Se considera que la integración de visualización en el proceso de MD puede ser de importancia significativa, ya que puede ayudar de dos maneras:
i. Proporcionar comprensión visual de complejas aproximaciones computacionales y;
ii. Descubrir relaciones complejas entre los datos que no son detectables por los métodos automáticos de análisis, pero que si pueden ser captados por el sistema visual humano.
De lo anterior, se deduce que la iteración alternada entre visualización y MD automática provee al analista de datos, soporte en la tarea de reconocimiento de patrones. Incluyendo al ser humano en este proceso, se logra una buena combinación de su percepción visual, con el poder de cálculo y almacenamiento del computador (Meneses & Grinstein, 2001). Hoy en día, existen pocas herramientas que incorporan visualización de modelos. Y las que existen son muy limitadas en su capacidad de exploración, y en responder preguntas acerca de las transformaciones, que realiza el modelo en los datos, para generar patrones (Keim & otros, 2010), (Castillo & Meneses, 2012).
3. Visualización para Modelos Clústeres
El análisis de clúster o clustering, es una tarea de MD que tiene por objeto identificar y describir grupos en un conjunto de datos, de tal manera que elementos asignados a un mismo grupo sean similares entre sí, mientras que elementos pertenecientes a grupos distintos sean disímiles (Yue, 2016). La medida de distancia es la más utilizada para realizar comparaciones entre atributos de las instancias. El proceso de clustering es utilizado para generar levantamiento de perfiles, y según el contexto de aplicación permite identificar grupos de: clientes, trabajadores, pacientes de hospitales, etc. (Maimon & Rokach, 2010).
Existen varios métodos para generar los agrupamientos, y cada uno utiliza un principio de inducción diferente. Por ejemplo, Fraley y Raftery proponen 2 tipos de métodos de clustering: jerárquicos y de particiones (Fraley & Raftery, 2007). Han y Kamber proponen, 3 tipos de clustering basados en: densidad, modelos y rejillas (Han & Kamber, 2006).
Se pueden encontrar diversos tipos de visualizaciones para modelos de clústeres:
· Coordenadas Paralelas: este diagrama se compone de un eje horizontal y varios ejes verticales. Cada eje vertical representa a una variable, cuyos valores son representados a lo largo de su eje horizontal. Para variables numéricas, los valores se ordenan de menor a mayor. Cada línea poligonal de este diagrama corresponde a una instancia o fila del conjunto de datos, y se mueve entre los ejes verticales dependiendo de los valores que le corresponde en cada variable. Este gráfico acompañado con elementos de interacción como transparencia y filtros, provee una visualización potente para objetos con muchas dimensiones.
· Gráfico de Dispersión: permite observar la relación que existe entre dos variables numéricas, y corresponde al tipo de gráfica más utilizada para modelos de clustering. Cada punto corresponde a los valores en las coordenadas (x, y). A cada grupo se le asigna un color y sus instancias también toman ese color, de esta forma es fácil identificar a que grupo pertenecen. Las instancias del conjunto de datos son graficadas con un máximo de 3 dimensiones.
· Matriz de Diagramas de Dispersión: es una generalización de un diagrama de dispersión que permite observar de manera simultánea, el comportamiento de variables numéricas en varias dimensiones. Es una herramienta de exploración de datos, que permite comparar un conjunto de instancias con respecto a todos sus atributos. Este gráfico muestra todas las combinaciones de gráficos de dispersión entre dos variables, en una sola vista bajo una estructura matricial. Para n dimensiones se muestran n filas y columnas.
· Dendrograma: es la forma más simple en la cual una estructura jerárquica de datos puede ser representada, y corresponde a un gráfico con forma de árbol (dendro; significa árbol). Los ítems de datos son representados por las hojas en el nivel final de la estructura del árbol, mientras que los nodos en el nivel más alto, son los que representan a los grupos o clústeres de los ítems de datos, con diversos niveles de semejanza (Jain & otros, 1999). La manera clásica de representar el dendrograma es dibujarlo como árbol enraizado, con la raíz anclada centralmente en el tope de la imagen, y las ramas de los nodos-hijos hacia abajo utilizando líneas derechas o diagonales.
· RadViz: es una técnica de visualización de coordenadas radiales. Muestra todos los atributos como puntos anclados al perímetro de una circunferencia, y separados en forma equidistante dependiendo de la cantidad de atributos. Dentro del círculo, se muestran las instancias en forma de puntos, los cuales están dispuestos en el gráfico. Toma como base al paradigma del tensor proveniente de la física de partículas, puntos de la misma clase se atraen entre sí, los de diferente clase se repelen, y las fuerzas resultantes se ejercen sobre los puntos de anclaje. Una ventaja de RadViz es que conserva simetrías de los datos, y su desventaja es la superposición de puntos (Hoffman & Grinstein, 2002).
· Diagrama de Voronói: aplicable a técnicas que generan centroides, y consiste en una partición del espacio euclidiano. Para cada par de centroides, se crean bisectrices perpendiculares, las cuales generan segmentos paralelos entre ellos. Este tipo de visualización para clúster genera polígonos para cada grupo, donde las instancias se distribuyen en su interior.
· Densidad de Grupos: corresponde a una visualización donde se pueden observar las densidades de cada grupo. Se muestra la región que cubre cada clúster, y se puede realizar análisis de las instancias.
· Gráfico de Radar: en este gráfico cada instancia es graficada como un polígono en un espacio radial, y sus aristas son generadas en relación a la magnitud de sus dimensiones, las instancias pertenecientes a mismos grupos presentan los mismos colores. Las figuras geométricas que presenten similitudes en su estructura corresponden a objetos similares.
4. Revisión de Trabajos Relacionados
El primer trabajo analizado corresponde a una solución de visualización para modelos de clústeres jerárquicos, propuesta por Long, cuya hipótesis principal es que existen dos grandes problemas para visualizarlos (Long, 2011):
La gran cantidad de datos limita la visualización de un modelo de clústeres, ya que el espacio en pantalla no permite observar todas las instancias.
Cuando el número de dimensiones es mayor a 3, no se pueden visualizar todos los atributos simultáneamente.
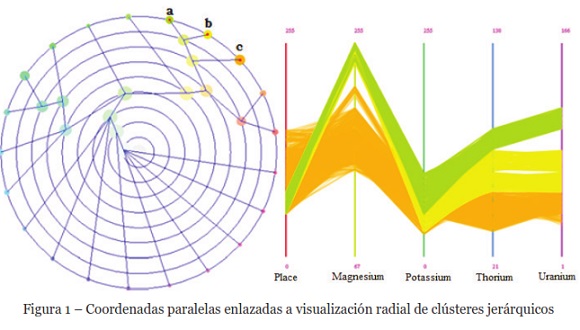
Esta propuesta de solución consiste en dos pasos: clustering y visualización. Con esto ayuda a los analistas de datos, a entender la distribución de un conjunto de datos con alta dimensionalidad. En el primer paso, se utilizan técnicas de algoritmos jerárquicos para generar clústeres. En el segundo paso, se proporcionan dos métodos para visualizar los resultados. El primer método de visualización utiliza un gráfico optimizado de estrellas, que minimiza el solapamiento. En el segundo método de visualización, se combinan las técnicas de; coordenadas paralelas, disposición radial para estructuras jerárquicas, y coordenadas paralelas circulares. La Figura 1, muestra la utilización de coordenadas paralelas enlazadas con visualización radial de árboles jerárquicos. El diagrama de coordenadas paralelas ubicados en la parte derecha, es desplegado interactivamente con la selección de clústeres del lado izquierdo.
En el ejemplo de la Figura 1, se muestran las coordenadas paralelas correspondientes a los nodos a, b y c seleccionados previamente en el gráfico jerárquico, estos representan la concentración de minerales. Se puede observar en el diagrama de coordenadas paralelas, que los nodos a (verde) y b (amarillo) presentan una mayor cantidad de magnesio que el nodo c, y el nodo a presenta una mayor cantidad de uranio con respecto a los otros dos nodos seleccionados. A través de la selección de instancias es posible realizar comparaciones de componentes del modelo generado.
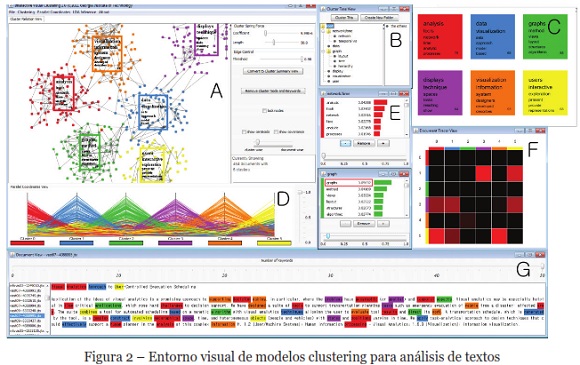
Un segundo trabajo relacionado plantea un entorno visual interactivo para modelos de clustering, en un contexto de análisis de documentos de textos, y que genera grupos con base en la frecuencia de las palabras. La Figura 2, muestra la interfaz principal de este entorno visual, en la cual existen diversos elementos para el análisis de clúster: coordenadas paralelas, vistas de relación para clústeres, vistas de árboles, entre otros. Este esquema visual provee diversos mecanismos de interacción para refinar resultados de un proceso de clustering. También permite filtración de datos fuera de rango y re-agrupamiento de datos (Lee & otros, 2012).
Se puede ver en el ejemplo de esta Figura 2, en la sección principal del entorno, que existen 454 documentos que son segmentados en 6 grupos. Esta sección principal denominada A, está acompañada con otras 6 secciones que aportan vistas complementarias y vinculadas al modelo, etiquetadas con las letras B hasta la G. En la sección A se ve cómo se relacionan los documentos de cada clúster, el clúster rojo se relaciona con el clúster verde, naranja y azul. En la sección B se tiene una vista de árbol de clústeres, en donde se mantiene la estructura jerárquica con tópicos definidos por el usuario. En la sección C se ven las palabras que más se repiten en los documentos, y en la sección D las coordenadas paralelas vinculadas entre los clústeres. La sección E corresponde a una vista donde se muestra el peso de cada palabra. La sección F presenta una vista de trazado de documentos con un gráfico mapa de calor, que muestra los cambios de miembros que han ocurrido entre clústeres. Finalmente, en la sección G se pueden seleccionar documentos interactivamente y se despliega el texto con las palabras marcadas.
El tercer trabajo revisado tiene relación con métricas que se utilizan para la comparación de instancias de clústeres. En este aspecto, Grabusts presenta un trabajo donde realiza un análisis de los resultados obtenidos por el algoritmo K-medias, con un conjunto de datos determinado. Para la generación de los clústeres, utiliza las métricas: distancia Euclidiana, distancia de Manhattan y coeficiente correlación de Pearson. Se concluye en este estudio, que los resultados obtenidos son muy similares con cada métrica utilizada, y que la correlación de Pearson, le entrega mejores valores para todos los clústeres (Grabusts, 2011).
En cuanto a la evaluación de modelos de clustering, en la literatura existen diversos criterios, que se dividen en internos y externos, para la evaluación de clústeres. No obstante, sólo algunos de estos son aplicados, entre los cuales destacan: la suma del error cuadrático (SSE), el índice de Dunn, y el índice de Davies-Bouldin (Maimon & Rokach, 2010). El análisis de clúster es considerado como un proceso de aprendizaje no supervisado, es decir el resultado no puede ser comparado con un valor conocido previamente. Por lo tanto, las matrices de confusión y las métricas de precisión utilizadas en tareas predictivas, no son aplicables para estos casos.
Los criterios de evaluación internos miden la compacidad de los clústeres a través de alguna medida de similitud, y por lo general miden la homogeneidad y separabilidad dentro de los clústeres, para esto consideran las distancias: intra-clúster e inter-clúster. Esto permite comparar cuantitativamente instancias de distintos clústeres, y medir el nivel de homogeneidad de los clústeres, lo cual permite conocer la conformación de los grupos generados por el proceso de clustering. En cuanto a los criterios de evaluación externos, pueden ser útiles para examinar si la estructura de los clústeres coincide con alguna clasificación previa. En estos casos se realiza una clasificación previa del conjunto de datos y posteriormente se comparan los resultados. Por ejemplo, para una secuencia de datos temporales con alta dimensionalidad, se puede aplicar el análisis de componentes independientes para la extracción de sus características (Zhu, 2015).
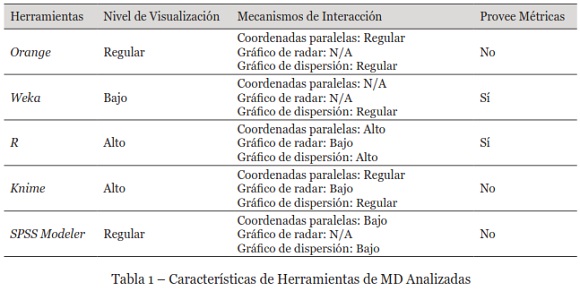
Por otro lado, también se revisaron 5 herramientas de MD entre las más utilizadas hoy en día, en relación a la representación visual que ofrecen sobre modelos de clústeres, y particularmente: el nivel y calidad de visualización, si provee métricas, y el nivel de interacción en tres tipos de gráficos seleccionados. Se califica el nivel de visualización, considerando la cantidad de elementos visuales que la herramienta tiene. Si es menor a 2, su calificación es baja, si es igual a 2 se califica regular, y mayor a 2 es buena. Para medir el nivel de interacción en los gráficos, se tiene en cuenta el número de interacciones disponibles, por cada elemento visual: menor a 3 es bajo, entre 3 y 4 regular, y mayor a 4 es alto.
Se puede observar desde la Tabla 1, que R es la herramienta más completa, aunque no dispone del gráfico radar, y que junto a Weka son las únicas que proporcionan métricas para el análisis de clústeres. No obstante, R es un entorno de programación que maneja la generación de modelos y visualización, a través de código con la librería llamada Ggobi (Dianne & Deborah, 2007).
Finalmente, en esta revisión de trabajos relacionados, también se analizan dos enfoques que sirven como referencia para establecer las bases del diseño de la propuesta de este trabajo de investigación.
Por un lado, está el campo de Analítica Visual descrita por Keim y otros, que se centra en el proceso de análisis y manejo de grandes volúmenes de datos (heterogéneos y dinámicos), mediante integración del juicio humano sobre representaciones visuales, y mecanismos de interacción. Combina áreas de: visualización, MD, y estadística. En este enfoque, visualización es una etapa central del proceso, que se orienta no sólo a la descripción visual de datos (entradas), sino que es fundamental para la construcción del modelo (proceso), y para representar el conocimiento obtenido a través de patrones (salida) (Keim & otros, 2010).
El segundo enfoque tomado como referencia, es el esquema de Visualización Aumentada para Modelos (VAM) en un proceso de MD, propuesto por Castillo y otros. Este esquema considera como ejes centrales: visualización de modelos para su análisis exploratorio, modelos de percepción visual, mecanismos de interacción, combinación de técnicas de MD, y métricas para comparar componentes del modelo. Presenta un modelo de percepción visual e interacción del usuario, centrado en la etapa de construcción y ajuste del modelo en un proceso de MD, y establece una forma de explorar el modelo original y sus componentes, considerando las características o ejes indicados recientemente (Castillo & Otros, 2015).
5. Diseño del Esquema VIMC
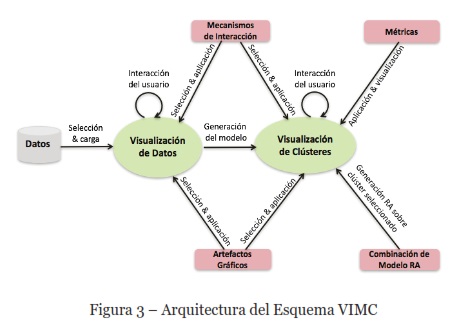
El esquema propuesto en este trabajo se denomina Visualización Interactiva para Modelos de Clústeres (VIMC), que permite al analista de datos explorar y analizar visualmente un modelo de clústeres, en la etapa de construcción y ajuste. Está orientado principalmente a tratar conjuntos de datos de alto volumen y alta dimensionalidad, y su arquitectura de diseño se puede observar en la Figura 3. Este esquema, como se señala al final de la sección anterior, tiene como base dos enfoques: analítica visual (Keim & otros, 2010), y visualización aumentada de modelos (Castillo & Otros, 2015).
Como se puede ver en la Figura 3, el esquema VIMC consta de dos estados representados por óvalos: Visualización de Datos, y Visualización de Clústeres:
1) Visualización de Datos; en este primer estado el analista de datos puede interactuar para realizar análisis exploratorio sobre los datos, utilizando artefactos gráficos y mecanismos de interacción apropiados. Para esto, las funcionalidades requeridas son: seleccionar y cargar el conjunto de datos de entrada o vista minable. El conjunto de datos debe ser previamente preparado, ya que el esquema VIMC no considera la preparación preliminar de la vista minable. Esta preparación del conjunto de datos se puede realizar utilizando herramientas de extracción, transformación y carga, conocidas como ETL (Extract, Transform, Load).
2) Visualización de Clústeres; la transición a este segundo estado ocurre cuando el analista de datos solicita la generación del modelo de clústeres, y para esto debe indicar el número de clústeres como parámetro. El analista de datos en este estado, puede interactuar directamente con el modelo de clústeres generado, seleccionando y aplicando los mismos artefactos gráficos y mecanismos de interacción del primer estado. Adicionalmente, puede aplicar y visualizar métricas sobre los clústeres y sus instancias, así como también tiene la opción de generar modelos de RA sobre clústeres seleccionados. Esto último para obtener una vista complementaria de cada clúster.
Para dar soporte a estos dos estados, para el diseño de la arquitectura del esquema visual VIMC se consideran 4 elementos fundamentales, los primeros dos elementos deben estar disponibles para los dos estados; visualización de datos y visualización de clústeres. Mientras que los dos siguientes elementos, sólo deben estar disponibles para el segundo estado (visualización de clústeres):
i. Artefactos Gráficos: define un conjunto de artefactos gráficos vinculados, y apropiados para representar conjuntos de datos y modelos de clústeres, de gran volumen y alta dimensionalidad. Como resultado del estudio del arte se logran determinar los elementos visuales más apropiados, para abordar estas complejidades, estos gráficos son: matriz de diagramas de dispersión, coordenadas paralelas, gráfico de radar y circular.
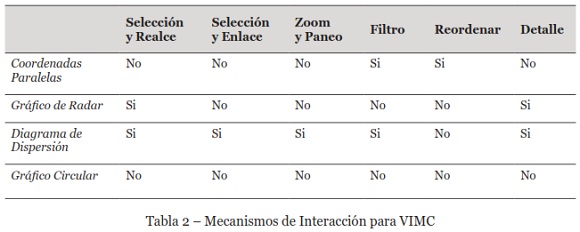
ii. Mecanismos de Interacción: establece la necesidad de contar con un conjunto de mecanismos de interacción ad-hoc para que el analista de datos, pueda moverse a través del conjunto de datos y el modelo de clústeres. De este modo, utilizando las diferentes vistas provistas por los artefactos gráficos y los mecanismos de interacción, el analista debe tener la posibilidad de recorrer y explorar las componentes o instancias, ya sea del conjunto de datos o del modelo de clústeres. Por ejemplo, seleccionando instancias de distintos clústeres para compararlas entre sí. Para esto, es necesario definir para cada artefacto gráfico, los mecanismos de interacción o acciones requeridas para apoyar estas labores, y en este caso son los que se indican en la Tabla 2:
iii. Métricas: una vez que el analista de datos genera el modelo de clústeres y pasa al segundo estado, requiere métricas para evaluar el modelo y comparar instancias de distintos clústeres, así como también para medir la compacidad o dispersión de cada clúster. Para esto, se consideran necesarias algunas métricas que utilizan criterios de evaluación interna. Se han seleccionado tres medidas: suma del error cuadrático medio (SSE), índice de Davies-Bouldin (DB-Index), y la distancia Euclidiana. Las dos primeras, se requieren para medir el nivel de compacidad o dispersión de los clústeres, y la tercera para la generación de los clústeres.
iv. Combinación de Modelo RA: en el segundo estado, el analista de datos puede obtener una vista complementaria de cada clúster, aplicando la técnica RA sobre un clúster seleccionado. Con esto, logra ampliar la descripción del modelo de clústeres, utilizando la capacidad de la técnica RA para determinar relaciones existentes entre atributos del conjunto de datos. La razón por la cual se ha seleccionada la técnica RA, radica en que se trata de una técnica descriptiva, que a través de reglas permite tener una mirada adicional de la conformación de los clústeres.
6. Implementación del Esquema VIMC
El esquema VIMC se implementa a través de un entorno visual web bajo una arquitectura cliente-servidor. El lado del cliente, se encarga de generar las visualizaciones e interacciones, y es en el servidor, donde se ejecutan los algoritmos de clustering y RA, y también se calculan las métricas. Se utiliza para la generación de los clústeres el algoritmo “K-medias”, y el algoritmo “A priori” para generar las RA. El entorno visual está desarrollado principalmente utilizando JavaScript tanto en el lado del cliente como del servidor. Su motor gráfico y de interacciones es D3.js. Para calcular las métricas y realizar las llamadas a los algoritmos de MD se utiliza Node.js.
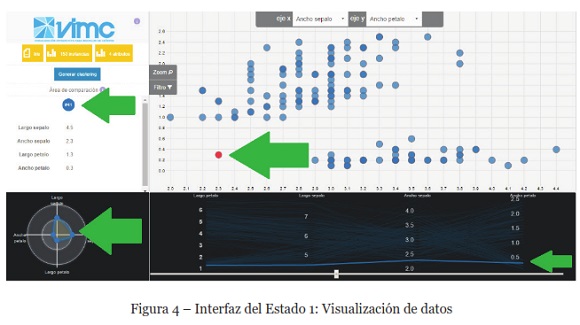
En la Figura 4, se presenta la interfaz principal del entorno visual, una vez que el usuario ha seleccionado y cargado el conjunto de datos a analizar. Esta parte representa el primer estado del esquema VIMC (visualización de datos). En este estado, el analista puede llevar a cabo un análisis multidimensional de los datos, pudiendo seleccionar múltiples instancias para ser comparadas. El diagrama de dispersión y las coordenadas paralelas son gráficas vinculadas, de modo tal que el usuario al seleccionar una instancia o variable en unos de los gráficos, se resalta automáticamente en el otro.
Además, en estos gráficos el usuario puede utilizar los mecanismos de interacción descritos para cada uno en la Tabla 2. La matriz de dispersión se presenta de a un diagrama, el usuario puede seleccionar los atributos que requiere para su análisis, a través de las coordenadas (x, y), los gráficos enlazados se actualizan de manera simultánea en la pantalla. Se puede observar además en esta misma Figura, dos instancias seleccionadas en color rojo, que son señaladas con flechas de color verde en el diagrama de dispersión, y simultáneamente son destacadas con líneas de color azul en el gráfico de coordenadas paralelas en la parte baja de la interfaz.
Los valores de los atributos de las instancias seleccionadas, son agregadas al área de comparación de la parte izquierda de la interfaz, como se indica también con una flecha verde, y son visualizadas en el gráfico de radar ubicado en el vértice inferior izquierdo. De esta forma, es posible comparar cuantitativamente dos o más instancias, con el objetivo de encontrar diferencias o similitudes en sus características.
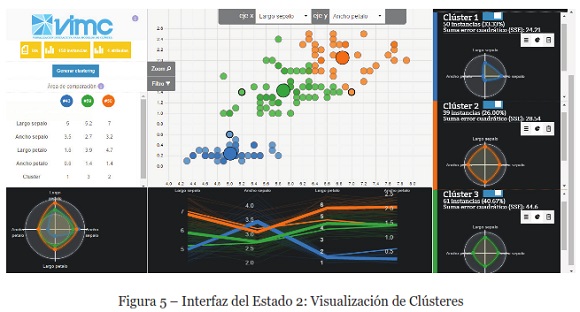
Una vez que el usuario hace clic en el botón de opción para generar el modelo de clústeres, se pasa al segundo estado en el esquema VIMC (visualización de clústeres), y la interfaz es la que se presenta en la Figura 5. Se puede apreciar que además de los gráficos y mecanismos de interacción provistos en el estado 1, el analista dispone de una vista multidimensional del modelo de clústeres generado, a través de una matriz de diagramas de dispersión que puede configurar según los atributos que requiera analizar, el cual también está enlazado con el gráfico coordenadas paralelas. Se colorean automáticamente las instancias de cada clúster en todas las vistas de los diferentes artefactos gráficos. En esta Figura aparecen 3 clústeres: azul para el clúster 1, naranja el clúster 2 y ver para el clúster 3.
También se puede observar, que aparece una nueva sección en el extremo derecho de la interfaz. En esta sección aparecen vistas complementarias que son provistas con: gráfico circular con los clústeres, la descripción de los clústeres junto al valor de sus métricas (SSE y DB-Index) y el gráfico de radar de cada clúster.
Adicionalmente, como se señala anteriormente, el usuario puede obtener vistas complementarias del modelo de clústeres, con la aplicación de una técnica de RA sobre cada clúster, la cual permite describir relaciones existentes entre atributos de las instancias. La técnica RA está disponible para cualquier conjunto de datos, y el usuario puede proporcionar como parámetro el porcentaje de confianza y cobertura requerido. Esto combinado con el gráfico de radar del clúster, puede complementar el análisis exploratorio de las RA, por ejemplo, puede determinar que atributos tienen más peso en un clúster. También, el gráfico de radar permite comparar los clústeres en cuanto a su compacidad o dispersión, ya sea a nivel de instancias como aparece en el vértice inferior izquierdo de la interfaz, como en la sección del extremo derecho a nivel de clústeres.
En resumen, el entorno visual del esquema VIMC incorpora todas las características y elementos definidos en el diseño de su arquitectura, entregando al usuario herramientas que le permitan analizar con mayor profundidad modelos de clústeres, en la etapa de construcción y ajuste dentro de un proceso de MD. Estas herramientas están orientadas, por un lado, a apoyar al análisis cualitativo o subjetivo del modelo a través de vistas complementarias y, por otro lado, apoyar el análisis cuantitativo u objetivo con el uso de las métricas implementadas, tanto para comparar instancias como para comparar clústeres.
7. Prueba, Evaluación y Resultados
Para estimar el valor práctico de las características definidas en el esquema VIMC e implementadas en un entorno visual web, se ha llevado a cabo un experimento controlado con usuarios experimentados en procesos de MD, para obtener sus percepciones subjetivas sobre la utilidad del esquema propuesto. Para esto, se ha diseñado una tarea de MD, que consiste en generar un modelo de clústeres a partir de un conjunto de datos determinado, para que los usuarios participantes en el experimento utilicen el entorno visual y desarrollen esta tarea. Luego, se ha diseñado una encuesta en línea que recoge las evaluaciones de las distintas características del esquema de visualización VIMC.
7.1. Descripción del Experimento
El experimento se realizó con un universo de 23 personas, los cuales tienen distintos niveles de experiencias en procesos de MD, y en el uso de herramientas de MD. La totalidad de los participantes tienen formación en informática a nivel de pre-grado y postgrado.
La experimentación se ha llevado a cabo en 3 etapas:
En primer lugar, los usuarios deben acceder a la siguiente URL: http://vimc.inf.unap.cl. En esta dirección, ellos encuentran un tutorial con animación que explica el trabajo de investigación, el acceso y uso del entorno visual, y también la encuesta en línea que deben responder, una vez que analicen el modelo de clústeres presentado.
Primera Etapa – Tutorial: en esta etapa, se explica el trabajo de investigación, y las características principales del esquema VIMC. También, el usuario conoce los aspectos generales del entorno visual.
Segunda Etapa – Entrenamiento: el usuario trabaja con el entorno visual y un conjunto de datos de entrenamiento, donde puede interactuar libremente generando un modelo de clústeres, comparar instancias, y aplicar RA en el modelo. El objetivo de esta etapa, es familiarizar al usuario con el entorno visual, y la usabilidad que proporciona para: generar, explorar y analizar un modelo de clústeres.
Tercera Etapa – Evaluación: en esta tercera etapa se presenta al usuario, el resultado del proceso de clustering con un segundo conjunto de datos, en el cual se han generado 2 clústeres. Además, ha sido aplicada la técnica RA al primer clúster, y dos elementos han sido seleccionados (uno de cada clúster). Esta etapa tiene como objetivo, que el usuario debe observar y analizar el modelo de clústeres presentado, para luego responder una encuesta en línea, la cual permite evaluar el esquema VIMC y el entorno visual.
El conjunto de datos utilizado en las etapas 1 y 2, es conocido como Iris, y contiene 150 registros de 3 tipos de flores. En donde los primeros 50 registros son del tipo Setosa, los siguientes 50 registros son Virgínica, y los últimos 50 registros son Versicolor. Cada registro tiene 4 atributos (longitud del pétalo, longitud del sépalo, anchura del pétalo, y anchura del sépalo).
Para la etapa 3, se utilizó el conjunto de datos llamado Wine que contiene 1000 registros de vinos con 12 atributos (acidez fija, acidez volátil, ácido cítrico, azúcar residual, cloruros, dióxido de azufre libre, dióxido de azufre total, densidad, pH, sulfatos, y grado de alcohol). No obstante, el entorno visual permite manejar cualquier conjunto de datos, y sólo se requiere que esté en el formato abierto CSV.
La encuesta diseñada para la validación del trabajo, consiste en 22 preguntas divididas en 6 secciones: información del participante, visualizaciones, análisis sobre el modelo de clústeres, análisis de RA, comparación de objetos, y sobre el esquema VIMC.
7.2. Discusión de Resultados
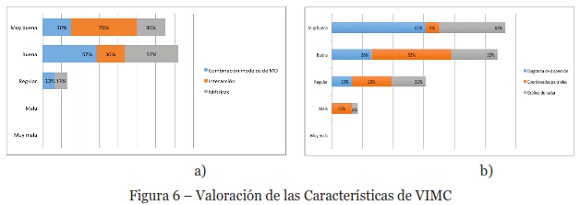
Todos los participantes, de la experimentación, expresan una alta valoración del esquema VIMC y su entorno visual. Respecto a las tres características del esquema propuesto, se puede observar desde el gráfico de la Figura 6 a), que la mayoría ha evaluado a la herramienta como muy buena con un 70%, y buena con un 30%, en relación al nivel de interacciones que proporcionan sus elementos visuales. La combinación de modelos de MD es bien considerada por los usuarios, con un 30% muy buena y 57% buena, y esta misma valoración obtienen las métricas que permiten comparar la compacidad y dispersión de los clústeres.
En relación al nivel de utilidad de los elementos visuales disponibles, para describir tanto datos como instancias en los clústeres, se puede observar desde el gráfico de la Figura 6 b), que los usuarios entregan la más alta valoración para el diagrama de dispersión, con un 87% de apreciación positiva (61% muy buena y 26% buena), en segundo lugar, al gráfico radar, con un 73% (dividida en 43% muy buena y 30% buena). Y, en tercer lugar, las coordenadas paralelas, con un 61% de valoración positiva (9% muy buena y 52% buena), y que, además, obtienen la mayor valoración negativa (26% regular y 13% mala).
Al consultar a los participantes si la generación de un modelo de RA sobre un clúster, ayuda a mejorar la comprensión de éstos, un 95% afirma que sí, mientras que sólo un 4% señala lo contrario. Cuando se les pregunta; si la comparación de instancias ayuda a comprender de mejor forma como se componen los clústeres, un 35% responde estar totalmente de acuerdo, un 57% está de acuerdo, y sólo un 9% no está de acuerdo. En cuanto a las métricas disponibles, un 30% de los usuarios considera que su utilidad es muy buena, un 57% cree que es buena, sólo un 13% piensa que es regular, y ninguno piensa que es mala o muy mala.
Una de las tareas del experimento tiene por objetivo, validar el análisis visual que consigue el usuario con la herramienta. Y para esto, el usuario debe observar dos clústeres, y luego determinar cuál de los dos es más disperso. Su respuesta es comparada con la métrica (SSE), que determina empíricamente la dispersión de los clústeres. Se obtiene como resultado que el 91% de los participantes, ha podido responder correctamente que clúster tiene mayor dispersión, y que corresponde al segundo clúster presentado. Esto es corroborado con su valor para SSE de 15.057, frente al primer clúster que sólo tiene un valor para SSE de 10.806.
Finalmente, frente a la pregunta: si el esquema VIMC, apoya la comprensión de un modelo de clústeres; el 48% de los participantes responde estar totalmente de acuerdo, y un 52% está de acuerdo. Esto significa que la totalidad de los participantes, evalúan positivamente el esquema visual propuesto.
8. Conclusiones y Trabajo Futuro
Respecto a las conclusiones obtenidas en este trabajo, destacan las siguientes:
· Los resultados del trabajo de investigación son muy alentadores, ya que la mayoría de los participantes en el experimento dan una valoración positiva sobre las características del esquema VIMC.
· El entorno visual logra una evaluación positiva en cuanto a: usabilidad, mecanismos de interacción, y gráficos implementados. Estos últimos, permiten un análisis exploratorio apropiado del conjunto de datos y del modelo de clústeres. Destaca la alta valoración de las interacciones implementadas en cada elemento visual, y también entre los artefactos gráficos, el diagrama de dispersión es el que obtiene mejor evaluación.
· En cuanto a las métricas provistas, si bien sus evaluaciones son buenas no son las que se esperaban, por lo que se considera una oportunidad de mejora para una próxima versión del entorno visual, principalmente en lo que se relaciona con visualización de estas métricas.
· La combinación de técnicas de MD, aunque es valorada positivamente la aplicación de RA sobre cada clúster, la idea es mejorar y evaluar su representación visual, de modo que sean más entendibles por parte de los usuarios.
· El esquema VIMC a través de su entorno visual, logra el objetivo de apoyar en la comprensión de un modelo de clústeres, en particular con conjunto de datos de alto volumen y alta dimensionalidad. El análisis visual del usuario en la experimentación, fue corroborado con métricas, y ambas medidas coinciden, por ejemplo, en reconocer si un clúster es más compacto que otro.
En relación al trabajo futuro, este tiene relación con los siguientes aspectos:
· Seleccionar y aplicar nuevos artefactos gráficos, que puedan ser de mayor utilidad en la exploración de los datos, y de los clústeres, preferentemente para conjunto de datos con alta dimensionalidad.
· Por el momento, VIMC utiliza el algoritmo K-medias con la distancia Euclidiana. Este algoritmo trabaja sólo con conjuntos de datos numéricos. Se propone incorporar otros algoritmos de clustering, y con otras medidas de distancia.
· Una mejora interesante, es integrar todos los algoritmos de MD que proporciona Weka.
REFERENCIAS
Castillo, W. & Meneses, C. (2012). A Comparative Review of Schemes of Multidimensional Visualization for Data Mining Techniques. III Congreso Internacional de Computación e Informática del Norte de Chile (INFONOR-CHILE). Arica – Chile.
Castillo, W., Meneses, C. & Medina, C. (2015). Augmented visualization for data-mining models. Journal: Elsevier Procedia Computer Science., 55, pp. 650-659. DOI: 10.1016/j.procs.2015.07.063 [ Links ]
Dianne, D. & Deborah, F. (2007). Interactive and Dynamic Graphics for Data Analysis: With R and Gobi, ISBN 978-0-387-71762-3. [ Links ]
Faria, B. M., Gonçalves, J., Reis, L. P., & Rocha, Á. (2015). A Clinical Support System Based on Quality of Life Estimation. Journal of Medical Systems, 39(10), 114. [ Links ]
Fraley, C. & Raftery, A. (2007). Model-based methods of classification: Using the mclust Software in Chemometrics. University of Washington Seattle, United States. DOI: 10.18637/jss.v018.i06. [ Links ]
Grabusts, P. (2011). The choice of metrics for clustering algorithms. Letonia. ISBN 978-9984-44-071-2. [ Links ]
Han, J. & Kamber, M. (2006). Data Mining: Concepts and Techniques, 2º ed., Estados Unidos, Elsevier. ISBN: 9781558609013. [ Links ]
Hoffman, P. & Grinstein, G. (2002). A Survey of Visualizations for High-Dimensional Data Mining, in: Fayyad U., Grinstein G. G., Wierse A. (eds.), Information Visualisation in Data Mining and Knowledge Discovery, Morgan Kaufmann Pub., San Francisco, pp. 47-85. [ Links ]
Jain, A., Murty, M. & Flynn, P. (1999). Data Clustering: A Review, ACM Computing Surveys, 31(3), pp. 264-323. [ Links ]
Keim, D., Kohlhammer, J., Geoffrey, E. & Mansmann, F. (2010). Mastering the Information Age Solving Problems with Visual Analytics. Edited by the authors Published by the Eurographics Association Postfach 8043, Printed in Germany, [ Links ] Druckhaus Thomas Müntzer GmbH, Bad Langensalza. Theoretical Issues in Ergonomics Science. Vol. 8, Nº 1, ISBN 978-3-905673-77-7.
Lee, H., Kihm, J., Choo, J., Stasko, J. & Park, H. (2012). iVisClustering: An interactive visual document clustering via topic modeling. In Computer Graphics Forum (Vol. 31, No. 3pt3, pp. 1155-1164). Blackwell Publishing Ltd. [ Links ]
Long, T. (2011). Visualizing High-density Clusters in Multidimensional Data. Bremen, Germany. DOI 10.1007/s00180-011-0271-3. [ Links ]
Maimon, O. & Rokach, L. (2010). Data Mining and Knowledge Discovery Handbook, 2nd ed. Springer Science+Business Media. Edited by Maimon and Rokach, Tel-Aviv University, Israel. ISBN 978-0-387-09822-7. [ Links ]
Meneses, C. & Grinstein, G. (2001). Visualization for Enhancing the Data Mining Process. In Proceedings of the Data Mining and Knowledge Discovery: Theory, Tools, and Technology III Conference. Orlando, FL.
Witten, I. H. & Frank, E., (2005). Data Mining: Practical Machine Learning Tools and Techniques, 2nd Edition. Morgan Kaufmann series in data Management Systems. ISBN: 0-12-088407-0. [ Links ]
Yue, W. (2016). Research on the Clustering Analysis Algorithm for Data Mining. Revista Ibérica de Sistemas y Tecnologías de la Información (RISTI), E6, pp. 209–221.
Zhu, Z. (2015). A Clustering Method for High-dimensional Data Analysis in Stock Market. Revista Ibérica de Sistemas y Tecnologías de la Información (RISTI), 17A, pp. 209–221.
Recebido/Submission: 24/03/2016
Aceitação/Acceptance: 27/04/2016