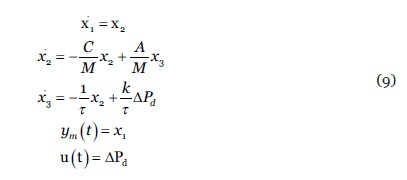ARTÍCULOS

Diseño de un Control Regulador para un Sistema de Servo-Posicionamiento Neumático

Regulation Control Design of a Pneumatic Servo-Positioning System

Iván Ramírez ¹, Christopher Toro¹, Jonathan Diaz²

¹ Universidad del Quindío, Ingeniería Electrónica, Departamento de Automatización y Control, 630004, Armenia, Quindío, Colombia. idramirez@uniquindio.edu.co, christop0217@hotmail.com

² Instituto Nacional de Astrofísica, Óptica y Electrónica INAOE, Maestría en Electrónica, 72840, Tonantzintla, Puebla, México. jdiazm@inaoep.mx

---

 

RESUMEN

Los actuadores neumáticos son de bajo costo, seguros, limpios y exhiben una alta relación potencia-peso. Esta contribución presenta una estrategia de control novedosa para resolver el problema de regulación de un sistema de servo posicionamiento neumático, que compensa por las no linealidades del sistema, considerando la posición, velocidad y la diferencia de presiones en las cámaras del cilindro neumático como estados de retroalimentación, en lugar de posición, velocidad y aceleración (PVA) como en los controladores más comunes que se encuentran en la literatura. Los experimentos son realizados con un cilindro neumático sin vástago, de 25 mm de diámetro y una válvula de control proporcional de 5/3 vías. Para probar la eficiencia y aplicabilidad del esquema de control propuesto tanto simulaciones como resultados experimentales se muestran y se discuten. Los resultados demuestran que un alto desempeño en posicionamiento y respuestas simétricas en el movimiento del deslizador en ambas direcciones puede ser logrado.

Palabras-clave: Lazo interno; estados de retroalimentación; sistema no lineal; lazo externo; control regulador.

---

 

ABSTRACT

Pneumatic actuators are low-cost, safe, clean, and exhibit a high power-to-weight ratio. This contribution presents a novel control strategy to solve the regulation problem of pneumatic servo positioning systems that cope with the nonlinearities of the system: airflow-pressure relationship through valve orifice and friction effects between contact  surfaces  in  actuator  seals,  by  considering the position, velocity and pressure difference in the chambers of the pneumatic cylinder, as feedback states instead of position, velocity and acceleration (PVA) as in the most common controllers found in literature. Experiments are conducted with a 25-mm bore rod-less pneumatic cylinder and a 5/3-way proportional control valve. To highlight the efficiency and applicability of the proposed control schemes, simulation, as well as experimental results are provided and discussed.

The experimental and simulated results from the regulation control strategy proposed, prove that high-positioning performance and symmetrical responses in forward and backward motion are achieved.

Keywords: Inner loop; linear feedback states; nonlinear system; outer loop; regulation control.

---

 

1. Introducción

Los actuadores neumáticos son ampliamente utilizados en el campo de la automatización, la robótica y la manufactura. Debido a sus atributos especiales, los actuadores neumáticos se han convertido en actuadores alternativos en tareas automatizadas de manejo de materiales. La tecnología neumática presenta muchas ventajas, como alta velocidad, alta generación de fuerza, mejor eficiencia, menos mantenimiento y bajos costos operativos. Sin embargo, su precisión relativamente baja les impide competir con sistemas electromecánicos, hidráulicos y magnéticos cuando se necesita una mayor precisión.

De otro lado, los actuadores neumáticos son difíciles de controlar debido a las características no lineales del sistema. Las no linealidades presentes en los actuadores neumáticos son la rigidez muy baja causada por la compresibilidad del aire en las cámaras del cilindro, las variaciones del caudal másico y la baja amortiguación del actuador, lo que dificulta el control preciso del movimiento (Saravanakumar, Mohan & Muthuramalingam, 2017). Otras no linealidades en los servosistemas neumáticos son la zona muerta de la válvula, saturación, ancho de banda limitado, relación no lineal flujo de aire-presión a través de los orificios de la válvula y los efectos de fricción entre las superficies de contacto en los sellos del actuador, especialmente en aquellas zonas con velocidad cercana a cero (Rahmat, M.F. et al., 2011), que son desfavorables en el diseño de estrategias para el control de servosistemas neumáticos en aplicaciones de posicionamiento de alta precisión (Ramírez, 2013).

Las altas no linealidades presentes en los sistemas neumáticos implica que sus modelos matemáticos se componen de ecuaciones diferenciales no lineales. Estas ecuaciones se caracterizan por no tener una solución explícita y por lo tanto requieren de un tratamiento exclusivo para cada solución. La teoría de los sistemas dinámicos no lineales permitió el acceso a nuevas herramientas matemáticas, capaces de permitir el análisis de modelos de sistemas más complejos con un comportamiento altamente no lineal que incluso puede alcanzar un comportamiento caótico.

En las últimas décadas, el modelado y control de actuadores servo neumáticos ha sido un tema interesante que ha atraído a investigadores de todo el mundo. Se deben identificar una gran cantidad de parámetros desconocidos para lograr una respuesta dinámica cercana a los sistemas reales. Las tres consideraciones principales para obtener el modelo de un sistema de actuador neumático son: (i) la dinámica de la carga, incluido el modelo de fricción porque la fuerza de fricción existente en el actuador neumático   lo hace difícil de controlar. Varios investigadores modelaron la fuerza de fricción para implementar compensación por fricción para una alta precisión en el desempeño del controlador. (ii) la presión, los volúmenes y la temperatura del aire en el cilindro, y (iii) el caudal másico a través de los orificios de la válvula (Sobczyk, Perondi & Suzuki, 2012).

(Valdiero, Ritter, Rios, & Rafikv, 2011) presentaron el modelo  de  un  sistema  de  servo posicionamiento como una combinación de ecuaciones teóricas y métodos de identificación del sistema. (Sorli, Gastaldi, Codina, & Heras, 1999) analizaron las características dinámicas de un sistema de posicionamiento servo neumático. Mientras que (Takosoglu, Dindorf, & Laski, 2009) presentaron el modelo teórico global del sistema servo neumático mediante el uso de una válvula proporcional. (Ramírez & Ibarguen, 2016) presentaron un modelo obtenido a partir de leyes físicas e identificación para obtener los parámetros del flujo compresible a través de los orificios de la válvula proporcional de control direccional. (Najafi, Fathi, & Saadat, 2009) modelaron la amortiguación del cilindro neumático al final de las carreras. (Ramírez, 2013) presentó un modelo global del sistema de servo posicionamiento neumático con el modelo de fricción LuGre incluido.

Muchos autores han presentado  diferentes  enfoques  de  control  y  algoritmos  para un control preciso de los actuadores neumáticos. Entre estos, (Aziz & Bone, 2000) presentaron un procedimiento de sintonización automático de los  parámetros  de  servo controladores para sistemas neumáticos; (Rao & Bone, 2008) presentaron una novedosa ley de control de posición no lineal de Múltiple entrada-una salida (MISO) diseñada mediante el uso del método de backstepping para sistemas neumáticos. Un método efectivo de compensación por fricción fue desarrollado en (Ning & Bone, 2002), que puede agregarse a cualquier estrategia de control. Cuando esta compensación la combinaron con el clásico enfoque de control posición-velocidad-aceleración/posición-velocidad (PVA/PV), alcanzaron experimentalmente una precisión de estado estacionario de ± 0.01 mm. (Tsai & Huang, 2008) propusieron un controlador adaptativo basado en la técnica de aproximación de función (FAT) para estimar las incertidumbres variables en el tiempo en los sistemas de servo-posicionamiento neumático. (Gulati & Barth, 2009) diseñaron un observador de presión basado en Lyapunov para un sistema servo neumático.

El diseño de sistemas de control complejos es difícil, sin embargo, es relativamente fácil utilizar controladores de lógica difusa, que utilizan una base de conocimiento, como   un operador humano. A manera de ejemplo, (Gao & Feng, 2005) desarrollaron un controlador adaptable Proporcional-Derivativo Fuzzy para el sistema de posicionamiento neumático. (Nagi & Perumal, 2009) optimizaron el controlador difuso para obtener una respuesta de tiempo mínima. (Kaitwanidvilai & Olranthichachat, 2011) propusieron una metodología robusta de un controlador difuso de formación de bucles para el control de posicionamiento del sistema servo neumático. (Gyeviki, Tóth, & Rózsahegvi, 2004) presentaron una estrategia de control por modos deslizantes y su aplicación      en un sistema de posicionamiento servo-neumático. (Ramírez, 2018) desarrolló una novedosa estrategia de control de seguimiento para el sistema de servo-posicionamiento neumático.

Por lo anterior, aunque muchos artículos cubren el control de los sistemas de servo-posicionamiento neumático, los controladores más comunes encontrados en la literatura usan PVA como los estados de realimentación. Esta contribución presenta una novedosa estrategia para resolver el problema de regulación de los sistemas de servo-posicionamiento neumático. El enfoque es novedoso en el sentido de que tiene en cuenta las no linealidades inherentes a los sistemas de servo posicionamiento neumático y considera la posición, la velocidad y la diferencia de presión en las cámaras del cilindro neumático como estados de retroalimentación. La estrategia de control diseñada es implementada en ambos: simulación y en el sistema de servo posicionamiento real.

Este documento está organizado de la siguiente manera: la sección 2 presenta una descripción del Sistema de Servo-Posicionamiento Neumático (SSPN) con sus componentes principales y el sistema neumático de prueba utilizado. La sección 3 presenta el modelo global del SSPN, desarrollado en (Ramírez & Ibarguen, 2016).      En la sección 4 se presenta la estrategia de control propuesta en este artículo para resolver el problema de regulación del SSPN, investiga experimentalmente el efecto de la realimentación de la diferencia de presión medida sobre el flujo no lineal a través    de los orificios de la válvula de control direccional proporcional de 5/3 vías utilizada. También se deriva la función de transferencia lineal y un modelo de espacio de estado para el SSPN. Esta sección también implementa el control regulador propuesto sobre el sistema neumático real y sobre el modelo de simulación global. La sección 5 concluye el documento con algunos comentarios y declaraciones finales.

2. Materiales y Métodos

2.1. Set-up experimental

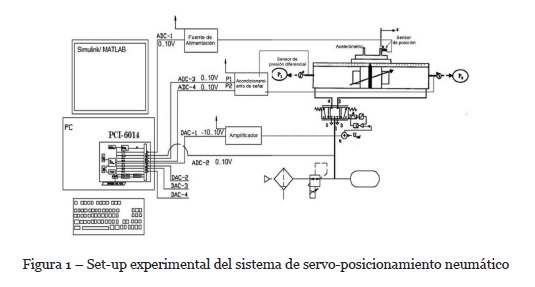
En la Figura 1 se muestra una representación esquemática de la configuración del sistema de servo posicionamiento neumático utilizado. Consiste de una válvula proporcional de 5 puertos (FESTO, MPYE-5-1/8 HF-010B) y un cilindro neumático sin vástago (FESTO, DGCI-25-1250-KF-YSR). El flujo de aire desde el tanque de aire a las cámaras del cilindro se rige en magnitud y dirección por la posición del spool de la válvula. Un actuador electromagnético (un solenoide) acciona el spool de la válvula. La parte electromecánica de la servo válvula se controla mediante un sistema de realimentación  con un ancho  de banda de aproximadamente 70 Hz, de modo que, en este rango de frecuencia, la posición del spool es aproximadamente proporcional a la señal de entrada. El cilindro sin vástago se usa para garantizar que el área de la sección transversal en ambas cámaras es la misma. El cilindro tiene un sistema de medición de posición integrado y es un sensor de posición de salida digital magnetoestrictivo (FESTO, CANBUS) con una resolución de 50 μm.

 

 

El deslizador interno (el pistón) se mueve hacia adelante y hacia atrás en el cilindro  por medio de aire seco aplicado a cada lado mediante el uso de la válvula de control direccional proporcional de 5/3 vías. La transferencia de movimiento al deslizamiento exterior se logra a través de un acoplamiento fijo. Para medir la presión dentro o en la entrada de las cámaras del cilindro, se adaptaron dos conexiones de aire comprimido y se usaron sensores de presión diferencial para medir la diferencia de presión entre las cámaras del cilindro, que es proporcional a la fuerza impulsora. La velocidad se puede obtener a partir de la integración de la de la aceleración obtenida del acelerómetro.

El sistema de adquisición y control utilizado es un NI DAQ PCI 6014 (National Instruments). Es un dispositivo electrónico especialmente diseñado para el desarrollo de control digital y adquisición de datos. Está compuesto por 16 entradas analógicas (ADC) y dos salidas analógicas (DAC). Se utiliza una computadora para proporcionar el voltaje de entrada de conducción a la válvula por medio de un convertidor D/A y leer los transductores por medio de convertidores A/D.

2.2. Diseño del control de regulación

El objetivo aquí es resolver el problema de regulación del SSPN considerado. Se propone una estrategia de control novedosa que compensa por las no linealidades del flujo de aire a través de los orificios de la válvula de control direccional proporcional de 5/3 vías y la fricción no lineal. La estrategia de control consta de dos partes:

 

 

Retroalimentación de estados (bucle externo) en el que la posición, la velocidad y la diferencia de presiones medida en las cámaras del cilindro neumático son los estados de retroalimentación. Este lazo compensará por la fricción no lineal para lograr un alto desempeño en posicionamiento.

Para investigar experimentalmente el efecto de la retroalimentación de la diferencia de presiones medida sobre las no linealidades del flujo de aire a través de los orificios de la válvula proporcional, se debe realizar lo siguiente: Separar el efecto del flujo no lineal desde la fricción no lineal. Esto se logra manteniendo el deslizador en una posición fija, que podría ser a la mitad de la carrera del cilindro neumático, es decir, considerando un subsistema que consiste en la válvula proporcional y dos cámaras aproximadamente iguales en tamaño.

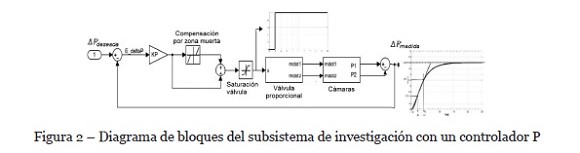
Aplicar un control proporcional para la diferencia de presiones con la compensación por zona muerta de la válvula proporcional dc, como se muestra en la Figura 2.

 

 

 

 

3. Resultados

3.1. Modelo de un sistema de servo-posicionamiento neumático

Un actuador neumático se puede modelar a partir de análisis matemáticos teóricos o a partir de la identificación del sistema. La mayoría de los investigadores han utilizado análisis matemáticos teóricos para modelar el actuador neumático, que requiere una combinación de termodinámica, dinámica de fluidos y dinámica de movimiento. Para construir el modelo matemático del SSPN, se deben tener en cuenta tres consideraciones principales: i) las tasas de flujo másico a través de los orificios de la válvula; ii) la presión, el volumen y la temperatura del aire en el cilindro; iii) la dinámica de la carga. El modelado preciso de un actuador neumático es una condición importante tanto  para el diseño del control como para optimizar su funcionamiento (Saravanakumar et al., 2017).

Esta sección presenta un modelo de simulación global del SSPN considerado, desarrollado en (Ramírez & Ibarguen, 2016). El modelo global del sistema de servo posicionamiento neumático consta de tres bloques principales: (i) la servo válvula; (ii) el actuador o cilindro neumático sin vástago y (iii) el deslizador del actuador neumático.

Para describir la dinámica del servo sistema en forma de modelo de espacio de estado, el modelo debe reformularse mediante un conjunto de ecuaciones diferenciales no lineales que describan relaciones únicas entre la entrada, la salida y los estados del sistema.

La representación más apropiada es la ecuación de estado para un sistema dinámico autónomo definido por la ecuación 2.

 

 

Para mayores detalles del modelo y de los valores de todas las constantes el lector puede remitirse a (Ramírez & Ibarguen, 2016).

3.2. Control de posicionamiento: Regulación

Identificación de la función de transferencia en lazo cerrado

 

 

Donde M: es la masa deslizante equivalente total, compuesta por la masa del pistón, la masa del deslizador y la masa de un objeto (pieza de trabajo) rígidamente acoplada  al deslizador; A: es el área de la sección transversal del pistón, y C: es el coeficiente de fricción viscoso. Finalmente, en la ecuación 7 se presenta la función de transferencia  de lazo cerrado del subsistema se identifica aplicando el modelo de primer orden más tiempo muerto (FOPDT) como en (Padma, Srinivas, & Chidambaram, 2004).

 

Modelo en espacio de estados del sistema de servo-posicionamiento neumático

 

Para describir este sistema dinámico en la forma del modelo de espacio de estado, el modelo debe reformularse mediante un conjunto de ecuaciones diferenciales de primer orden o ecuaciones en diferencia que describan relaciones únicas entre la entrada, la salida y los estados del sistema.

 

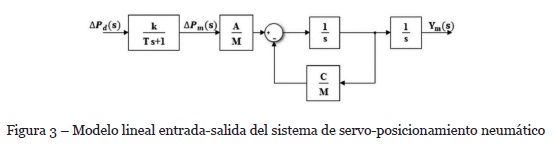
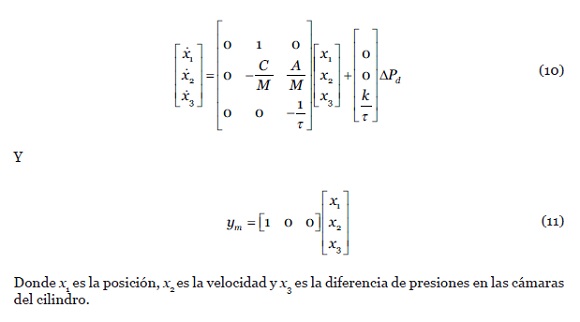
El modelo lineal de entrada-salida del SSPN es único y se puede utilizar para caracterizar el sistema a través de un conjunto único de ecuaciones diferenciales de primer orden, como se muestra en las ecuaciones 9:

 

A partir de las ecuaciones diferenciales anteriores, el sistema se puede describir en forma de espacio de estado, ecuaciones 10 y 11:

 

4. Discusión

En la sección anterior se estableció que un lazo de retroalimentación de la diferencia de presiones medida, embebido con un controlador proporcional y una compensación por zona muerta de la válvula, compensará por las no linealidades del flujo de aire a través de los orificios de la servo válvula.

Posteriormente, se diseña el control del lazo externo, es decir, en los estados en los que la posición, la velocidad y la diferencia de presión medida en las cámaras del cilindro neumático son los estados de retroalimentación. Este lazo compensará por la fricción no lineal para lograr un alto desempeño en posicionamiento.

4.1. Controlabilidad

 

4.2. Realimentación de estados

Con respecto al diseño del lazo externo (retroalimentación del estado) en la estrategia de control propuesta, la ecuación de estado del sistema servo neumático dado en la ecuación 10, puede reescribirse como se muestra en la ecuación 13:

 

4.3. Ubicación de polos

El sistema es controlable, por lo que todas las raíces de la ecuación característica del sistema en lazo cerrado se pueden colocar en cualquier ubicación deseada en el semiplano izquierdo del plano s. La ecuación característica deseada para el sistema de lazo cerrado se puede especificar como en la ecuación 19:

 

4.4. Implementación de la estrategia de control propuesta para solucionar el problema de regulación

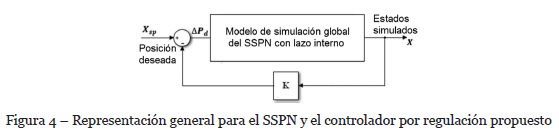
La estrategia de control propuesta está implementada en el sistema de servo posicionamiento neumático real. La Figura 4 muestra una representación general del sistema servo neumático y el controlador regulador propuesto.

 

 

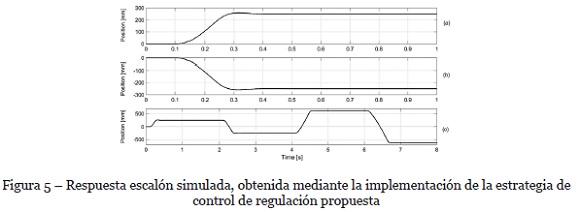
Las respuestas simuladas de la posición del deslizador ante entradas paso obtenidas usando la estrategia de control propuesta se representan en la figura 5. Los resultados demuestran que un alto desempeño en posición (bajo tiempo de subida, sobre impulso despreciable y error de estado estacionario insignificante) es alcanzable. Es importante notar la simetría de la respuesta del deslizador en avance (+250 mm) y en retroceso (-250 mm).

 

 

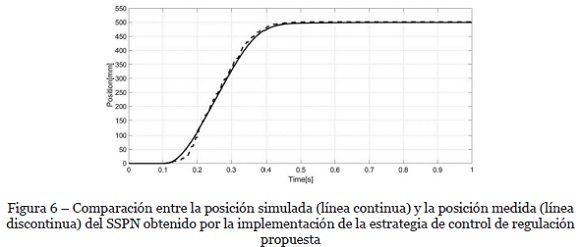
La figura 6 muestra una comparación entre la posición obtenida desde el modelo de simulación global y la posición medida en el SSPN experimental, obtenidas para una entrada paso en posición de 500 mm.

 

 

 

 

Los resultados demuestran que, con la estrategia de control propuesta en este artículo, el SSPN reproduce con mucha fidelidad el comportamiento del modelo de simulación global. El tiempo de retraso entre los resultados de la simulación y la posición medida es de aproximadamente 0.1 s. Este tiempo de retraso proviene del tiempo muerto introducido por los tubos de conexión entre la válvula y el cilindro y de posibles fugas en las conexiones del cilindro neumático real (la fuga máxima para un nuevo cilindro a 6 bar es de aproximadamente 10 litros/hora). En el modelo de simulación global, los tubos se modelaron como un volumen muerto en el cilindro, a pesar de que las fugas no fueron contempladas en el modelo del SSPN. Si se desea eliminar este tiempo de retraso, una posible alternativa es el uso de dos válvulas proporcionales 3/2. La evaluación de esta alternativa será objeto de futuros trabajos.

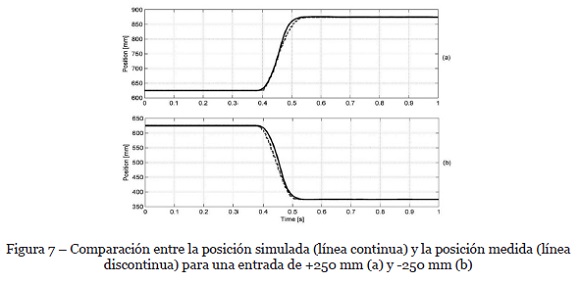
Con el fin de analizar la simetría en el comportamiento del deslizador en avance y en retroceso, se aplicaron dos entradas escalón de 250 mm en direcciones contrarias. La Figura 7 es una comparación entre las posiciones simuladas y medidas que se obtienen implementando la estrategia de control propuesta. Los resultados demuestran que se obtienen respuestas simétricas en el movimiento de avance y retroceso.

 

 

5. Conclusiones

 

 

Este lazo compensará por las no linealidades de la fricción modelada para lograr un alto desempeño del controlador por regulación.

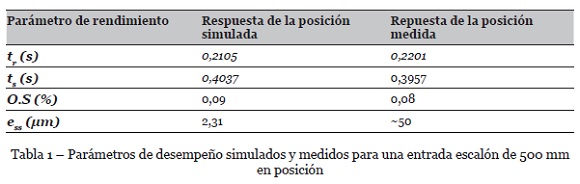
La principal limitación de la estrategia de control propuesta es el tiempo de retraso   que depende de las mangueras de conexión, del caudal de la válvula y del tamaño del cilindro neumático. El tiempo de retraso puede disminuirse utilizando dos válvulas proporcionales de 3/2. La evaluación de esta alternativa será objeto de una próxima publicación. Los resultados experimentales de la estrategia de control de regulación propuesta indican que se puede lograr un alto desempeño en posicionamiento  como   se muestran en la tabla 1. El bajo sobre impulso se traduce en un alto amortiguamiento en todas las ubicaciones a lo largo del cilindro neumático, un tiempo de subida pequeño y un error en estado estacionario del orden de la resolución del sensor de posición magnetostrictivo usado (50μm).

 

REFERENCIAS

Aziz, S., & Bone, G. M. (2000). Automatic tuning of pneumatic servo actuators. Advanced Robotics, 13(6), 563-576.         [ Links ]

Gao, X., & Feng, Z. J. (2005). Design study of an adaptive Fuzzy-PD controller for pneumatic servo system. Control Engineering Practice, 13(1), 55-65.         [ Links ]

Gulati, N., & Barth, E. J. (2009). A globally stable, load-independent pressure observer for the servo control of pneumatic actuators. IEEE/ASME Transactions on Mechatronics, 14(3), 295-306.         [ Links ]

Gyeviki, J., Tóth, I. T., & Rózsahegvi, K. (2004). Sliding mode control and its application on a servopneumatic positioning system. Transactions on Automatic Control and Computer Science, 49(63), 1-6.         [ Links ]

Kaitwanidvilai, S., & Olranthichachat, P. (2011). Robust loop shaping-fuzzy gain scheduling control of a servo-pneumatic system using particle swarm optimization approach. Mechatronics, 21(1), 11-21.         [ Links ]

Nagi, F., & Perumal, L. (2009). Optimization of fuzzy controller for minimum time response. Mechatronics, 19(3), 325-333.         [ Links ]

Najafi, F., Fathi, M., & Saadat, M. (2009). Dynamic modelling of servo pneumatic actuators with cushioning. The International Journal of Advanced Manufacturing, 42(7), 757-765.         [ Links ]

Ning, S., & Bone, G. M. (2002). High steady-state accuracy pneumatic servo positioning system with PVA/PV control and friction compensation. In IEEE International Conference on Robotics and Automation, 2824-2829.         [ Links ]

Padma, R., Srinivas, M. N., & Chidambaram, M. (2004). A simple method of tuning PID controllers for stable and unstable FOPTD systems. Computers & Chemical Engineering, 28(11), 2201-2218.         [ Links ]

Rahmat, M. F., Sunar, N. H., Najib-Salim, S., Mastura-Shafinaz, Z. A., Mohd-Fauzi, A. A., & Ismail, Z. H. (2011). Review on modelling and controller design in pneumatic actuator control system. International Journal on Smart and Intelligen Systems, 4(4), 630-661.         [ Links ]

Ramírez, I. (2013). Modelling and tracking control of a pneumatic servo positioning system. In II international Congress of Engineering Mechatronics and Automation (CIIMA).         [ Links ]

Ramírez, I. (2018). Design of a tracking controller of a siso system of pneumatic servopositioning. Ingeniería y Desarrollo, 36(1), 74-96.         [ Links ]

Ramírez, I., & Ibarguen, F. (2016). Nonlinear control of a servo-pneumatic positioning system. Scientific and technical report No 695. Universidad del Quindío, Colombia.         [ Links ]

Rao, Z., & Bone, G. M. (2008). Nonlinear modeling and control of servo pneumatic actuators. IEEE Transactions on Control Systems Technology, 16(3), 562-569.         [ Links ]

Saravanakumar, D., Mohan, B., & Muthuramalingam, T. (2017). A review on recent research trends in servo pneumatic positioning systems. Precision Engineering, 49, 481-492.         [ Links ]

Sobczyk, M. R., Perondi, E. A., & Suzuki, R. M. (2012). Feedback linearization control with friction compensation applied to a pneumatic positioning system. ABCM Symposium Series in Mechatronics, 5, 252-261.         [ Links ]

Sorli, M., Gastaldi, L., Codina, E., & De las Heras, S. (1999). Dynamic analysis of pneumatic actuators. Simulation Practice and Theory, 7(5), 589-602.         [ Links ]

Takosoglu, J. E., Dindorf, R. F., & Laski, P. A. (2009). Rapid prototyping of fuzzy controller pneumatic servo-system. The international Journal of Advanced Manufacturing, 40, 349-361.         [ Links ]

Tsai, Y. C., & Huang, A. C. (2008). FAT-based adaptive control for pneumatic servo systems with mismatched uncertainties. Mechanical Systems and Signal Processing, 2(6), 1263-1273.         [ Links ]

Valdiero, A. C., Ritter, C. S., Rios, C. F., & Rafikov, M. (2011). Nonlinear mathematical modelling in pneumatic servo position applications. Mathematical Problems in Engineering, 2011, 1-16.         [ Links ]

 

Recebido/Submission: 26/07/2018

Aceitação/Acceptance: 09/09/2018