Serviços Personalizados
Journal
Artigo
Indicadores
Links relacionados
Compartilhar
RISTI - Revista Ibérica de Sistemas e Tecnologias de Informação
versão impressa ISSN 1646-9895
RISTI no.37 Porto jun. 2020
https://doi.org/10.17013/risti.37.99-115
ARTIGOS
Math2Text: Software para geração e conversão de equações matemáticas em texto - limitações e possibilidades de inclusão
Math2Text: Software for generating and converting mathematical equations to text - limitations and inclusion possibilities
Albino Szesz Junior1 2, Lucas Ribeiro Mendes2, Sani de Carvalho Rutz da Silva2
1 Departamento de Informática, Universidade Estadual de Ponta Grossa UEPG, 84030-900, Ponta Grossa/PR, Brasil. alsjunior@uepg.br
2Universidade Tecnológica Federal do Paraná UTFPR - Ponta Grossa, 84015-150, Ponta Grossa/PR, Brasil. lrmen14@gmail.com, sani@utfpr.edu.br
RESUMO
No campo da inclusão, especificamente na deficiência visual, identificam-se lacunas para compreensão e interpretação de equações matemáticas presentes em diferentes mídias. Assim, objetiva-se neste trabalho apresentar o Math2Text, um produto que converte equações, produzidas em uma plataforma gráfica, em equações textuais acessíveis, através do formato de “texto lido”, o qual é obtido por extenso e sem ambiguidades, possibilitando ao estudante com deficiência visual compreender e interpretar a equação, a fim de solucioná-la adequadamente. Para tanto utilizou-se a metodologia DCU, design centrado no usuário, com as seguintes etapas: pesquisa, design, prototipagem e teste. Na pesquisa foram analisados estudos similares, realizando uma comparação entre diferentes softwares. Na etapa de design apresentam-se as ferramentas e a estratégia a ser utilizada durante o desenvolvimento. Na prototipagem apresenta-se a ferramenta e suas interfaces, por fim, na etapa de teste, demonstra-se o teste realizado com um professor e um grupo de alunos com deficiência visual. Conclui-se que o sistema se mostrou bastante eficiente e pretende, num futuro próximo, automatizar todo o processo.
Palavras-chave: Conversão de equações para texto, Acessibilidade, Inclusão, Deficiência visual, Software.
ABSTRACT
In the field of inclusion, specifically when it comes to vision difficulties, there are gaps for understanding and interpreting mathematical equations presented on different media. Thus, the objective of this work is to present Math2Text, a product that converts equations produced in a graphical platform to accessible textual equations, through the format of “read text”, i.e., a string of unambiguous text written in a natural language (e.g., Portuguese), with the goal of enabling visually impaired students to understand and interpret equations so they can be solved properly. For this purpose, the UCD (User-centered design) methodology was used, with the following steps: research, design, prototyping and testing. In the research phase, similar studies were analyzed, and different software were compared. In the design stage, the tools and strategy used in the development are presented. In prototyping, the tool and its interfaces are presented, then in the test stage, the test performed with a teacher and a group of visually impaired students is demonstrated. It is concluded that the system proved to be quite efficient and, as future work, it is intended to automate the whole process.
Keywords: Conversion of equations to text, Accessibility, Inclusion, Visual impairment, Software.
1. Introdução
Nas últimas décadas, o ser humano teve uma grande evolução na chamada inclusão social, que tem por objetivo incluir a todos no mesmo contexto social, auxiliando cada indivíduo de acordo com suas necessidades, para que todos participem do ambiente social da forma mais igualitária possível.
Diante da pauta da inclusão, a acessibilidade foi buscada em diversas áreas da vida e do trabalho humano, inclusive na área de computadores e internet, através da acessibilidade virtual e das tecnologias assistivas.
A acessibilidade virtual está relacionada à capacidade de sua utilização por pessoas com deficiência, permitindo que estes usuários sejam capazes de perceber os conteúdos, compreendê-los, realizar atividades de navegação e interação, bem como criar conteúdo na web (W3C BRASIL, 2013).
Já o termo tecnologias assistivas (TA) é utilizado para identificar todo um conjunto de recursos e serviços que contribuem para proporcionar ou ampliar habilidades funcionais de pessoas com deficiência e consequentemente promover vida independente e inclusão (Bersch, 2017).
Assim, na busca por acessibilidade virtual e na utilização das tecnologias assistivas, uma área de aplicação se dá as pessoas com deficiência visual, que necessitam, em grande parte dos casos, de formas auditivas bem detalhadas, baseadas nos conceitos de audiodescrição, para compreender informações visuais presentes em mídias, computadores ou na internet.
Esta área, segundo dados da Organização Mundial de Saúde (OMS) a cegueira afeta aproximadamente 39 milhões de pessoas em todo o mundo, número que aumenta para 246 milhões considerando perda moderada ou severa da visão (Augusto et al., 2019).
Neste sentido, Bonilla, Silva e Machado (2018) destacam que a distinção entre cegueira e baixa visão se baseia mais em critérios funcionais que em critérios médicos, sendo considerado indivíduos com baixa visão aqueles que, podendo inclusive ser considerados legalmente cegos, são capazes de utilizar o resíduo visual que possuem para executar tarefas do dia a dia, especialmente as de caráter escolar.
Assim, os mesmos autores afirmam que independente do grau, causa, ou momento do aparecimento, é importante perceber que a deficiência visual não é um problema por si e esses indivíduos têm potencial para um desenvolvimento considerado normal a depender do ambiente físico e social no qual estejam inseridos.
Afirmação que vem de encontro com as teorias de Vigotski (1997) que consideram que a cegueira, bem como outras deficiências, pode promover uma reorganização completa no funcionamento psíquico, de modo a possibilitar uma compensação do impedimento, considerando que o problema da cegueira é meramente instrumental, e ao se proporcionar ao cego formas alternativas de acesso aos aspectos da cultura inacessíveis a ele devido à ausência de visão, o problema será contornado, como no caso do sistema braile, que permite ao cego o acesso à linguagem escrita (de Lira & Schlindwein, 2008).
Na busca por proporcionar formas alternativas de acesso ao conhecimento, muitas tecnologias assistivas foram desenvolvidas como recursos didáticos. Estes recursos didáticos, vão desde os mais tradicionais (óculos bifocais e monofocais, lupas, bengala, reglete, sorobã, régua para escrita cursiva, máquina Perkins para escrita em braille, dentre outros) até os mais avançados (calculadoras e relógios que falam, bengalas com sensor laser, etiquetas com gravação de áudio, identificador de notas de dinheiro e de cores, dentre outros) (Bonilla et al., 2018).
Com o avanço das tecnologias através do computador e da internet, esta área teve um impulso maior, possibilitando que as pessoas com deficiência visual utilizem: teclados com letra ampliada e contraste, software para ajuste de cores e tamanho das informações (efeito lupa), software leitores de tela, softwares de reconhecimento de voz, softwares leitores de texto impresso (OCR), software para impressão aumentada, impressora braille, impressão em relevo, linha braille, dentre outros (Bonilla et al., 2018).
Estes recursos fazem parte das tecnologias assistivas, as quais na visão de Radabaugh (1993) tornam, para as pessoas sem deficiência, as coisas mais fáceis e para as pessoas com deficiência, tornam as coisas possíveis.
Neste sentido, este trabalho busca produzir uma ferramenta que tornem as coisas mais fáceis e possíveis, mas também uma tecnologia capaz de auxiliar pessoas que buscam educação e não possuem condições de adquirir softwares com licenças pagas, cumprindo o papel da tecnologia definido por Rocha & Angélico (2015, p. 10) “[...] as Tecnologias de Informação (TI) assumem um papel determinante [...] como um instrumento primordial para a concretização da aquisição e transferência de conhecimento e, concomitantemente, para a modernização, reforma e transformação do processo educativo, há vários anos.”.
Neste sentido, o produto desenvolvido neste trabalho, tem por objetivo converter equações produzidas em uma plataforma gráfica para equações textuais acessíveis, através do formato de “texto lido”, que é o texto por extenso, ou seja, uma leitura literal da equação matemática, sem ambiguidades, possibilitando ao estudante com deficiência visual compreender a equação e assim formulá-la da maneira correta, afim de solucioná-la adequadamente.
Clique ou toque aqui para inserir o texto.O processo de desenvolvimento deste trabalho, seguiu a abordagem do design centrado no usuário (DCU) (Anderson et al., 1988; ISO 9241-210, 2019), que foca no desenvolvimento de soluções com a geração de produtos bem adaptados às características e necessidades dos usuários, que sejam fáceis de usar e úteis, esse processo é dividido nas etapas de pesquisa, design, prototipação e teste.
Costa et al. (2015) ao aplicar essa metodologia (DCU) no desenvolvimento de uma plataforma de ensino de matemática, nos diz que o envolvimento dos utilizadores no processo de desenvolvimento providencia uma fonte de conhecimento sobre o contexto de utilização, sobre as tarefas e como os utilizadores tendem a trabalhar posteriormente com o software.
Assim, neste artigo será apresentado o Math2Text um produto de software web, desenvolvido através da metodologia do design centrado no usuário (DCU) e proveniente da junção de softwares de código aberto e códigos autorais, com o objetivo de auxiliar na interpretação de símbolos matemáticos para estudantes com baixa ou nenhuma visão, bem como professores no desenvolvimento de materiais acessíveis.
2. A pesquisa para desenvolvimento do Math2Text
A notação matemática é baseada em uma variedade de símbolos, gráficos e diagramas que normalmente descrevem objetos abstratos que são impossíveis de se apresentar de forma linear sem o uso de vários parênteses. Essa não linearidade é o principal desafio ao se projetar uma ferramenta para a tradução automática de notação matemática. (Bier & Sroczyński, 2015, 2019; Spinczyk et al., 2019)
Diferentes abordagens foram usadas para a conversão automática de notação matemática para a forma falada e vice-versa. Uma solução possível para o sistema ler (ou escrever) notação matemática de maneira compreensível e adequada é equipá-la com uma ferramenta para tradução automática da notação simbólica matemática para a linguagem falada, tal como a apresentada por Cuartero-Olivera et al. (2012) e outra de síntese de fala como a desenvolvida por El-Glaly & Quek (2014), as quais necessitam de um conjunto de ferramentas, conhecimentos avançados e conhecimentos da língua inglesa, visto que as existentes, em sua grande maioria foram desenvolvidas neste idioma.
Dentre as ferramentas já desenvolvidas de TTS (Text-to-speech) destinados à matemática, a grande maioria necessita de um tipo específico de entrada tal como LATEX ou MathML, linguagens de marcação, e usam um conjunto de regras de tradução predefinidas no processo de tradução, bem como possuem acesso livre, não comercial.
Dentre as ferramentas e iniciativas já desenvolvidas neste âmbito destacam-se: Math Speak & Write (Guy et al., 2004), AudioMath (Ferreira et al., 2005), Tcitac (Caky et al., 2009), TalkMaths (Wigmore et al., 2009), i-Math (Wongkia et al., 2012), MathSpeak (Nazemi et al., 2012), 4Math (Sebastian et al., 2017) e Equation Wizard (Bier & Sroczyński, 2019).
Assim, realizando a primeira etapa do DCU, buscou-se embasamento para a pesquisa e o atual estado de produtos já desenvolvidos no âmbito da matemática e acessibilidade, realizou-se um levantamento sobre as funcionalidades presentes em sistemas já desenvolvidos. A escolha dos softwares para comparação baseou-se no levantamento bibliográfico realizado e em uma lista de ferramentas matemáticas elaborada pelo World Wide Web Consortium (W3C) (W3C Wiki, 2007), uma organização que visa padronizar a internet mundial, propondo padrões e boas práticas para utilização.
Assim, selecionou-se softwares com diferentes finalidades de exportação e disponíveis em diferentes plataformas, buscando analisar os fatores e características de cada um, para isso levantou-se os seguintes requisitos:
• Ferramenta: Identificação da ferramenta, nome utilizado.
• Licença: Identificação da licença do software, se é paga ou gratuita, possibilitando definir se pode ser usado por qualquer usuário ou se há restrições de uso devido a compra de software.
• Plataforma de Utilização: Plataformas nas quais a ferramenta pode ser utilizada, desktop, internet, dispositivos móveis. Demonstrando o quão amplo pode ser seu acesso ou se é restrito a determinados tipos de sistemas operacionais.
• Interface: Identificação do tipo de interface do software, se ele possui interfaces gráficas e intuitivas para melhor usabilidade do usuário ou se não possui, o que pode tornar mais difícil a manipulação da ferramenta.
• Tipos de Exportação: Formato de arquivos para exportação, limitando-se a avaliar se a ferramenta possui suporte a três tipos de exportação: LaTex, MathML e Equação para Texto, sendo a primeira um formato indicado para uso em textos científicos, a segunda para uso em plataformas WEB e a última para saídas acessíveis a deficientes visuais que utilizem leitores de tela. Quanto maior o número de exportações que a ferramenta abrange, maior será as possibilidades de uso para o usuário, que poderá adaptar e aplicar em diferentes plataformas e usos.
• Acessível: Identificação se a ferramenta possui saídas acessíveis, sendo o formato Equação para Texto um tipo de saída acessível. Esse fator identifica se a ferramenta de alguma forma contempla o âmbito da acessibilidade.
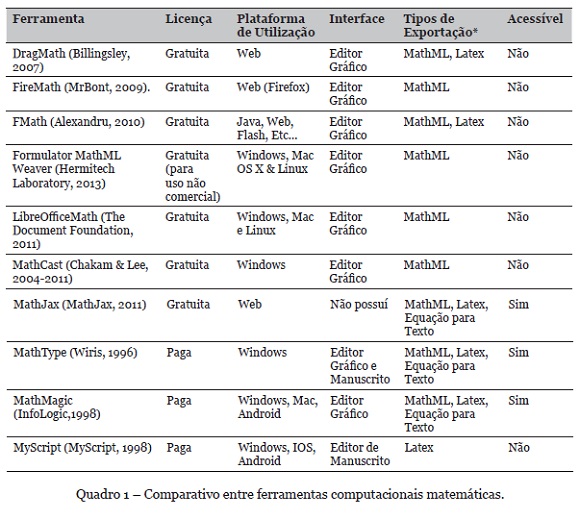
A partir disso, analisou-se os softwares encontrados e elaborou-se um comparativo entre ferramentas computacionais matemáticas, apresentados no Quadro 1.
Analisando-se o quadro 1, identifica-se que os softwares mais abrangentes, possuem licenças comerciais, bem como lacunas, como a falta de distribuição gratuita, saídas em formatos científicos como LaTex e MathML e suporte à diferentes sistemas operacionais, características consideradas no desenvolvimento do produto, objeto deste trabalho.
Na análise, também se observou que as ferramentas de uso gratuito, em grande parte, possuem maior reportação de erros pela comunidade que a utiliza, sendo que muitas não possuem nenhum tipo de suporte ou encontram-se em estado de abandono por parte dos desenvolvedores, isto é, tratam-se de softwares sem atualizações ou correções há anos, fato identificado a partir da consulta nos respectivos repositórios/sites dos softwares.
Essa baixa quantidade de softwares acessíveis e o abandono em seu desenvolvimento, pode estar relacionada as especificidades necessárias na produção de ferramentas acessíveis, pois exige do desenvolvedor a compreensão das limitações humanas e o conhecimento das formas de adaptar seu software.
Relacionando o quadro 1 elaborado com as referências estudadas, enfatiza-se que a maioria das soluções apresentadas suporta apenas o idioma inglês, incluindo as ferramentas comerciais citadas e que devido à gramática e semântica, essas soluções não podem ser usadas diretamente para outros idiomas nacionais.
Observa-se também a necessidade de preparação do material em formatos específicos (XML, LaTeX) bem como a instalação de softwares específicos, não gera autonomia ao professor e ao deficiente visual, assim falta uma solução flexível, que permita adaptação e que seja de fácil uso para todos os envolvidos.
Porém, constata-se que há duas ferramentas presentes no mercado que alcançam a maioria dos fatores listados no Quadro 1, o MathType e o MathJax.
O MathType faz parte de uma suíte de softwares de produção matemática para computadores da companhia Wiris. A ferramenta produz desde o desenvolvimento de equações em editores gráficos até sua exibição final em websites, porém possui licença paga, o que inviabiliza o acesso a todos.
O MathJax é uma ferramenta gratuita, constantemente atualizada, possuindo um grande universo de colaboradores e empresas que auxiliam no seu desenvolvimento e manutenção. Apresenta saídas acessíveis compatíveis com diversos leitores de tela gratuitos, além de outros formatos acessíveis para exibição de equações. Contudo, trata-se apenas de uma ferramenta de exibição de equações em plataformas web, tornando-a menos abrangente que a suíte do MathType.
A ferramenta Math2Text (produto) desenvolvido neste trabalho, busca aliar as qualidades de ambas ferramentas, buscando uma solução completa que vai desde a criação da equação até sua exibição online com saídas acessíveis no idioma português brasileiro, sendo distribuída de forma gratuita.
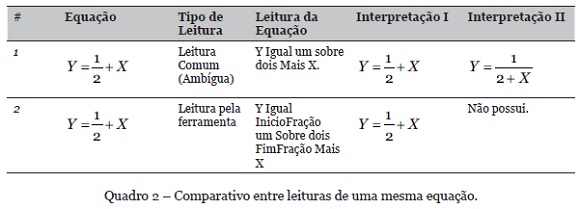
Outro ponto considerado no desenvolvimento do produto, relaciona-se com a forma de leitura de uma equação, pois diferente da forma padrão de apresentar uma equação matemática em braile, que encontra-se no Código Matemático Unificado (2006), a transcrição de uma equação para um texto, afim de ser lido por um software leitor de tela, deve ser feito de forma não ambígua, utilizando os conceitos de audiodescrição, pois o usuário deve conseguir formular a equação de maneira correta. Contudo, não se encontrou nenhum padrão claro estabelecido para tal transcrição, assim, busca-se uma forma baseada em uma leitura literal da equação com todos seus componentes, evitando qualquer possível ambiguidade na interpretação da equação. O Quadro 2 apresenta a diferença entre uma leitura de equação comum (ambígua) e a leitura produzida pela ferramenta.
A partir do Quadro 2, observa-se que uma mesma equação pode ser interpretada de diferentes formas, por exemplo, na equação 1, não realizando a diferenciação entre denominadores e fatores da equação, gerando ambiguidade, afim de resolver isto, todos os componentes são descritos de maneira literal, tal como é realizado na equação 2, descrevendo o início e fim da fração.
3. Design do Math2Text
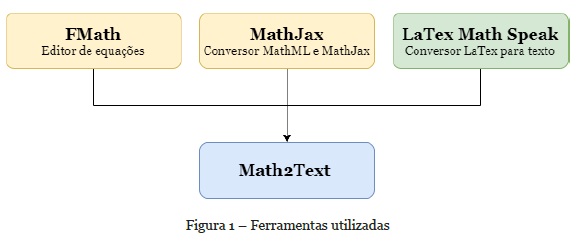
Após a realização da etapa de pesquisa do DCU, a próxima etapa é de design, com a busca e a produção de uma solução, para isso no desenvolvimento do Math2Text foram utilizadas duas ferramentas externas (FMath e MathJax) e uma autoral (LaTex Math Speak), todas com distribuição gratuita, cada qual com um intuito diferente, que juntas se tornaram o Math2Text (Figura 1).
A ferramenta FMath (Ionel Alexandru, 2010) é distribuída sobre a licença de software livre Apache 2.0, e possui um editor de equações desenvolvido em diferentes linguagens de programação, compatível com diversas plataformas. A versão utilizada neste trabalho foi o FMath baseado em Javascript, uma linguagem de programação amplamente utilizada na web, logo, compatível com o produto deste trabalho.
O objetivo principal da FMath é proporcionar ao usuário uma ferramenta visual bastante intuitiva, para que seja possível formular equações, das mais simples até as mais complexas. Além disso, o FMath permite converter a equação produzida para diferentes formatos, tal como LaTex e PNG, o que é essencial para o funcionamento do produto desenvolvido.
O MathJax (MathJax, 2011), como citado anteriormente, trata-se de um conjunto de códigos que facilitam o uso de equações matemáticas em sistemas para internet. Também é produzido em Javascript, permitindo a interoperabilidade com as demais ferramentas utilizadas, além de possuir suporte a grande maioria dos navegadores e distribuída com licença de software livre Apache 2.0.
A ferramenta possui suporte nativo à diferentes ferramentas de acessibilidade, permitindo que sua abrangência seja ampliada através da utilização e desenvolvimento de plugins elaborados por diferentes pessoas, permitindo mais funcionalidades à ferramenta principal.
No produto desenvolvido, o MathJax é responsável pela geração das saídas em formato MathML e MathJax.
A ferramenta LaTex Math Speak foi desenvolvida pelos autores a fim de realizar a junção e adaptação das demais ferramentas existentes, já citadas, com o objetivo da pesquisa.
Foi desenvolvida com a linguagem e programação PHP, na qual possui como entrada uma equação em formato LaTex, originada da ferramenta FMath, e então transformada em uma equação em formato texto acessível com duas diferentes opções, simples e detalhada.
A forma detalhada denomina-se “Formato Texto Completo” e a forma simples denomina-se “Formato Texto Resumido”, ambas transcrevem a equação com mais ou menos detalhes, contudo, nenhuma delas deve gerar ambiguidade em sua interpretação por parte do usuário que a escuta. A figura 2 exemplifica uma equação apresentada em ambos os formatos produzidos pela ferramenta.
No exemplo, apresentado na Figura 2, o formato “texto completo” considera todos os termos da equação, delimitando o início e fim de todos, início e fim de equação, fração, numerador, denominador, já a forma “texto resumido” delimita apenas o início e fim do elemento fração.
4. Prototipação do Math2Text
A próxima etapa da metodologia DCU foi a prototipação, O Math2Text, como citado, originou-se da junção de diferentes softwares, proporcionando uma aplicação voltada para web automatizada, na qual o usuário deve produzir sua equação em um editor online e então a transformar, gerando saídas em diferentes formatos, na sequência serão apresentadas as interfaces do produto desenvolvido.
Destaca-se que no desenvolvimento da interface do protótipo, foram considerados os princípios de usabilidade de Nielsen (1993), buscando simplicidade, assim o produto possui duas telas, a principal, na qual o usuário produz a equação por meio do editor gráfico e a tela de resultados, que retorna ao usuário a equação em diversos formatos de saída, incluindo o modo texto acessível.
4.1. Interfaces do Produto
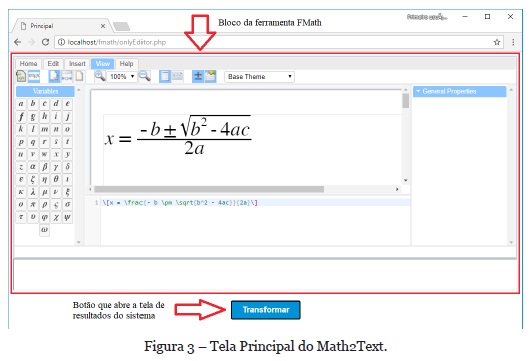
A tela inicial do produto (Figura 3), possui um bloco com o editor gráfico de equações FMath, pela qual o usuário, por meio de menus, pode desenvolver diversos tipos de equações matemáticas, além do botão “Transformar” que, ao ser pressionado, gera a produção de saídas ao sistema em uma nova tela.
Nesta tela (Figura 3), no desenvolvimento da interface, buscou-se um design padronizado, dividindo as ações semelhantes em cada aba e exibindo todas as informações de escolha do usuário como números, variáveis, sinais, operações, etc., em botões padronizados e com ícones que representam a ação do botão. Tais fatores buscam proporcionar ao usuário uma melhor compreensão das ações e a padronização dos componentes na tela. Assim, o design da ferramenta pretende cumprir os fatores da intuitividade e memorização, presentes na usabilidade de software (Nielsen 1993).
O botão “Transformar” foi inserido em tamanho ampliado e com cores diferenciadas, com um texto sugestivo, localizado na área central da tela, abaixo do bloco do Editor de Equações, o que indica ao usuário um componente externo de controle, que, a partir da ação de clicar no botão “Transformar” os resultados são apresentados em uma nova interface,
Os resultados são apresentados na Tela de resultados (Figura 3), a qual tem por função exibir todas as saídas produzidas pelo sistema de maneira objetiva e organizada, buscando cumprir os critérios da facilidade de memorização e intuitividade no quesito da usabilidade de software (Nielsen 1993).
A tela divide as informações em blocos de um mesmo padrão, identificando qual saída está presente em cada bloco, proporcionando ao usuário a possibilidade em compreender quais saídas foram geradas e a de utilizar-se dos resultados da forma que necessitar.
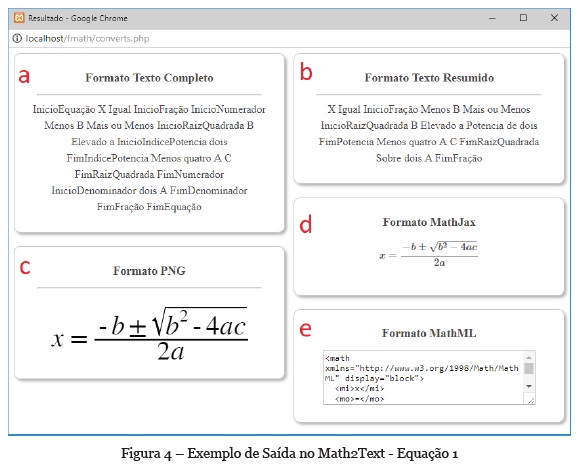
A fim de demonstrar as possibilidades a partir do produto desenvolvido, na figura 4, será apresentado um resultado obtido a partir da fórmula de Bhaskara, uma fórmula que possui diversos componentes e símbolos matemáticos.
Nesta tela (Figura 4), observa-se quatro diferentes formatos de saída para a equação, sendo eles:
1. Texto (a, b): Saída da equação em formato de texto completo(a) e resumido(b), realizando a demarcação dos elementos da equação, objetivando uma interpretação não ambígua e utilização através de leitores de tela.
2. PNG (c): Saída em formato de imagem com fundo transparente, comumente utilizada na produção de diferentes mídias (livros, e-books, sites, etc)
3. MathJax (d): Saída em formato MathJax, que permite utilização em aplicações online através de um interpretador integrado nos principais navegadores.
4. MathML (e): Saída em linguagem de marcação MathML para web, formato recomendado e mantido pela W3C, organização que padroniza a web.
Para exemplificar, na figura 5, é apresentado um novo exemplo de saída a partir de uma equação diferente.
A partir dos resultados apresentados, destaca-se a saída da equação em formato de texto acessível, objetivo principal da pesquisa, a qual possibilita, a partir de sua inserção em materiais didáticos desenvolvidos em diferentes mídias, aos usuários com baixa ou nenhuma visão, compreender a equação por meio da leitura (auditiva) através de leitores de tela, de forma bem estruturada e sem ambiguidade, conseguindo assim formulá-la corretamente.
Como citado, a saída textual possui dois retornos, sendo o formato “completo” que possui a equação explicada de uma forma detalhada e com todas as informações estruturais possíveis, e o formato “resumido” que detalha a equação de forma mais simples, sendo o primeiro mais recomendado para equações complexas e o segundo para equações simplificadas.
5. Teste do Math2Text
A próxima etapa da metodologia DCU foi o teste, o protótipo desenvolvido foi testado e avaliado com o envolvimento dos usuários, para avaliação do Math2Text. Realizou-se um teste com um professor de matemática e grupo de cinco deficientes visuais com ensino médio completo e que utilizaram o leitor de tela NVDA para leitura no sistema operacional Windows, com o objetivo de verificar se a ferramenta funcionaria em um ambiente real.
O professor elaborou uma lista de 5 equações simples através do Math2Text, são elas: 1+1, 4-2, 10x10, 10/5 e √4 devendo o grupo de alunos ler através do leitor de tela e responder oralmente. As equações foram apresentadas ao grupo de deficientes visuais em dois momentos através do navegador.
No primeiro momento, apresentação sem a descrição textual, apenas em formato MathML e com o leitor de tela ativo, os estudantes não conseguiram identificar nenhuma das equações, então no segundo momento apresentou-se as mesmas equações com as descrições textuais obtidas a partir do Math2Text e solicitou que tentassem ler novamente e então respondessem oralmente. Todos os estudantes conseguiram identificar as equações e responder corretamente o resultado das operações.
Após o teste, os estudantes apresentaram feedbacks positivos, registrados por meio das observações e vídeo, sugeriram uma maior abrangência e a disseminação do software desenvolvido, o qual, na visão deles, seria de muita importância para a comunidade com deficiência visual. O professor destacou que o processo de desenvolvimento das equações através do Math2Text é fácil, porém trabalhoso, sugere que se busque mais automatização no processo, tal como também discutido nos trabalhos de Bier & Sroczyński (2019) e Spinczyk et al. (2019).
Essa primeira versão do Math2Text vem ao encontro que expressões matemáticas na internet ou em outras mídias digitais, muitas vezes são encontradas em formatos não acessíveis, como imagens (png, jpeg), que somente podem ser lidas por softwares leitores de tela caso sejam descritas como texto alternativo, o que normalmente necessita de conhecimentos específicos de programação, além de ser oneroso descrever textualmente cada uma das equações de forma manual, assim o protótipo desenvolvido neste trabalho tinha o objetivo de automatizar esse processo de descrever textualmente.
O teste objetivava verificar o funcionamento do Math2Text, como parte do processo DCU utilizado, após o teste o processo volta ao início, de forma cíclica, permitindo seu refinamento em novas versões.
6. Considerações finais sobre o Math2Text
O desenvolvimento do Math2Text teve por foco principal a conversão de equações produzidas em plataforma gráfica para equações textuais acessíveis, objetivo que foi em grande parte conquistado, porém, como todo projeto em desenvolvimento, não é possível definir a abrangência total da ferramenta, pois seus resultados dependem da complexidade das equações nela produzidas e de sua própria atualização por parte do desenvolvedor.
O sistema se mostrou bastante eficiente, contudo necessita de mais testes e refinamentos, pretende-se realizar automatização do processo facilitando o desenvolvimento de materiais por parte do professor, bem como novos testes com expressões mais complexas serão desenvolvidos, tanto com outro grupo de alunos, quanto com professores, a fim de conscientizá-los e capacitá-los na utilização dessas ferramentas e em uma atitude inclusiva na sala de aula.
O Math2Text no formato em que se encontra poderia estar disponibilizado, porém ainda serão realizados mais testes e algumas adaptações, sendo em breve disponibilizado através do site do grupo de pesquisa de forma gratuita e seu código fonte será disponibilizado na internet abertamente, permitindo que qualquer usuário possa utilizá-lo e alterá-lo conforme sua necessidade, sem nenhum tipo de custo.
7. Conclusão
A partir do exposto neste trabalho com o levantamento dos principais aspectos do produto desenvolvido, tais como a característica de software livre, aplicação voltada para web, diferentes padrões de saída, acessibilidade, considera-se que o mesmo possibilita um grande auxílio para usuários que necessitam de ferramentas acessíveis e atingiu-se o objetivo proposto no trabalho.
O produto será disponibilizado com código aberto em repositório de software, a fim de permitir a comunidade ajudar em sua melhoria e desenvolvimento colaborativo, beneficiando-se por meio de auxílios externos de usuários que compreendem o problema e querem fazer parte de sua solução.
A próxima etapa da pesquisa objetiva automatizar o processo, permitindo que qualquer equação elaborada em MathML possa ser lida corretamente pelo leitor de tela, não necessitando uma conversão e elaboração de material específico com os textos acessíveis obtidos a partir da saída do produto.
Destaca-se que ainda há muito trabalho a ser realizado na área de inclusão, porém iniciativas como as apresentadas neste trabalho, alinhando tecnologia e acessibilidade, impactam na vida de todos, proporcionando meios para professores elaborarem materiais didáticos acessíveis, bem como a possibilidade de uma correta interpretação de equações matemáticas, de forma autônoma, pelo deficiente visual. Assim, o desenvolvimento da pesquisa cria um caminho a ser percorrido por trabalhos futuros e traça um horizonte com grandes expectativas.
O presente trabalho foi realizado com o apoio do Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq), Brasil.
REFERÊNCIAS
Anderson, N. S., Norman, D. A., & Draper, S. W. (1988). User Centered System Design: New Perspectives on Human-Computer Interaction. The American Journal of Psychology, 101(1), 148. DOI: https://doi.org/10.2307/1422802. [ Links ]
Alexandru, I. (2010). Fmath (Software). Recuperado em 09 outubro 2017 de: http://www.fmath.info [ Links ]
Augusto, J., Ottaiano, A., Pereira De Ávila, M., Caixeta, C., Alexandre, U., & Taleb, C. (2019). As Condições de Saúde Ocular no Brasil 2019. 1. ed. São Paulo: Conselho Brasileiro de Oftalmologia, 2019. Recuperado em 21 fevereiro 2020 de: http://www.cbo.com.br/novo/publicacoes/condicoes_saude_ocular_brasil2019.pdf
Bersch, R. (2017). Introdução à Tecnologia Assistiva. Recuperado em 20 novembro 2019 de: http://www.assistiva.com.br [ Links ]
Bier, A., & Sroczyński, Z. (2019). Rule based intelligent system verbalizing mathematical notation. Multimedia Tools and Applications, 78(19), 28089-28110. DOI: https://doi.org/10.1007/s11042-019-07889-3. [ Links ]
Bier, A., & Sroczyski, Z. (2015). Adaptive math-To-speech interface. In ACM International Conference Proceeding Series, 29-30-Jun-2015, 1-9. DOI: https://doi.org/10.1145/2814464.2814471. [ Links ]
Billingsley, A. (2007). DragMath (Software). Recuperado em 20 novembro 2017 de: https://sourceforge.net/projects/dragmath [ Links ]
Bonilla, M. H. S., Silva, M. C. C. C. da, & Machado, T. A. (2018). Tecnologias digitais e deficiência visual: a contribuição das TIC para a prática pedagógica no contexto da Lei Brasileira de Inclusão. Revista Pesquisa Qualitativa, 6(12), 412. DOI: 10.33361/rpq.2018.v.6.n.12.236. [ Links ]
BRASIL. Ministério da Educação. (2006). Código matemático unificado para a língua portuguesa. [ Links ]
Caputo, M., Cheng, J., Duffield, C., Putnam, C., Wozniak, K., & Zefeldt, M. (2012). How Do Professionals Who Create Computing Technologies Consider Accessibility?. New York: ACM. DOI: 10.1145/2384916.2384932 [ Links ]
Caky, P., Boron, J., Klimo, M., & Bachratá, K. (2009). Mathematical formulas in text to speech system, 11, 49-53.
Cercone, N. & Naruedomkui, K. & Wongkia, W. (2012). i-Math: Automatic math reader for Thai blind and visually impaired students. Computers & Mathematics with Applications, 64(6). DOI: 10.1016/j.camwa.2012.04.009.
Chakam, T. & Lee, Timothy. (2004). MathCast (Software). Recuperado em 20 novembro 2017 de: http://mathcast.sourceforge.net [ Links ]
Correia, R. C., Miranda, T. G., & Santos, L. C. M. (2018). Tecnologias: Caminhos para a acessibilidade um relato de experiência. Trabalho apresentado em Anais do Congresso Brasileiro de Educação Especial. DOI: 10.17648/galoa-cbee-6-30167. [ Links ]
Costa, A. P., Coelho, E. B., Tavares, L. C., & Freitas, F. (2015). Envolvimento dos Utilizadores na definição de Requisitos: O caso da plataforma WEBMAT. RISTI - Revista Iberica de Sistemas e Tecnologias de Informacao, E4, 92-106. DOI: 10.17013/risti.e4.92-106. [ Links ]
Cuartero-Olivera, J., Hunter, G., & Pérez-Navarro, A. (2012). Reading and writing mathematical notation in e-learning environments. ELearn Center Research Paper Series, 4, 11-20. Recuperado de: http://elcrps.uoc.edu [ Links ]
de Lira, M. C. F., & Schlindwein, L. M. (2008). A pessoa cega e a inclusão: Um olhar a partir da psicologia histórico-cultural. Cadernos CEDES, 28(75), 171-190. DOI: https://doi.org/10.1590/s0101-32622008000200003 [ Links ]
El-Glaly, Y. N., & Quek, F. (2014). Digital reading support for the blind by multimodal interaction. In ICMI 2014 - Proceedings of the 2014 International Conference on Multimodal Interaction, 439-446. DOI: 10.1145/2663204.2663266 [ Links ]
Ferreira, H., Ferreira, H., & Freitas, D. (2005). AudioMath: Towards Automatic Readings of Mathematical Expressions. In Humancomputer Interaction International (HCII), Las Vegas. http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.581.7685
Guy, C., Jurka, M., Stanek, S., & Fateman, R. (2004). Math Speak & Write, a Computer Program to Read and Hear Mathematical Input. http://www.cs.queensu.ca/drl/ffes/ [ Links ]
Hermitech Laboratory. (n.d.). Formulator MathML Weaver (Software). Recuperado em 21 novembro 2017 de: https://sourceforge.net/projects/formulator-math [ Links ]
InfoLogic. (1998.). MathMagic (Software). Recuperado em 21 novembro 2017 de: http://www.mathmagic.com [ Links ]
ISO 9241-210. (2019). ISO 9241-210: 2019, Ergonomics of human-system interaction - Part 210: Human-centred design for interactive systems. In International Organization for Standardization (p. 32). https://www.iso.org/standard/77520.html.
MathJax (2011). MathJax (Software). Recuperado em 20 outubro 2017 de: https://www.mathjax.org [ Links ]
MrBont. (2009). FireMath [Software]. Recuperado em 29 novembro 2017 de: http://www.firemath.info [ Links ]
MyScript (1998). MyScript Nebo: The Best Way to Take Notes (Software). Recuperado em 24 novembro 2017 de: https://www.myscript.com/nebo [ Links ]
Nazemi, A., Murray, I., & Mohammadi, N. (2012). Mathspeak: An audio method for presenting mathematical formulae to blind students. In International Conference on Human System Interaction, HSI, 48-52. DOI: https://doi.org/10.1109/HSI.2012.17. [ Links ]
Nielsen, J. (1993). Usability Engineering. Boston, USA: Academic Press. [ Links ]
Radabaugh, M. P. (1993). Study on the Financing of Assistive Technology Devices of Services for Individuals with Disabilities - A report to the president and the congress of the United State, National Council on Disability, Março 1993. Recuperado em 04 dez. 2017 de: http://www.ccclivecaption.co [ Links ]
Rede Nacional de Ensino e Pesquisa (RNP). (2016). Mercado de TI sofre com falta de profissionais qualificados. Recuperado em 26 julho 2018 de: https://www.rnp.br/destaques/mercado-ti-sofre-falta-profissionais-qualificados [ Links ]
Rocha, Á. & Angélico, M. (2015). Information Technology (IT) in Education. RISTI - Revista Ibérica de Sistemas y Tecnologías de Información, (16), ix-xii. DOI: 10.17013/risti.16.ix-xi [ Links ]
Sá, E. D. (2005). Acessibilidade: as pessoas cegas no itinerário da cidadania. Revista da Educação Especial/MEC, 1(1), 13-18. [ Links ]
Sebastian, M., Ckowski, M., Franciszek Brzoza, P., & Spinczyk, R. (2017). Tutoring math platform accessible for visually impaired people. DOI: 10.1016/j.compbiomed.2017.06.003. [ Links ]
Spinczyk, D., Maćkowski, M., Kempa, W., & Rojewska, K. (2019). Factors influencing the process of learning mathematics among visually impaired and blind people. Computers in Biology and Medicine, 104, 1-9. DOI: 10.1016/j.compbiomed.2018.10.025. [ Links ]
The Document Foundation (2011). LibreOffice Math (Software). Recuperado em 05 dezembro 2017 de: https://www.libreoffice.org [ Links ]
Vigotski, L. S. (1997). Obras escogidas: fundamentos de defectologia. Madrid: Visor. [ Links ]
W3C BRASIL. (2013). Cartilha de Acessibilidade na Web: W3C Brasil. https://www.w3c.br/pub/Materiais/PublicacoesW3C/cartilha-w3cbr-acessibilidade-web-fasciculo-I.html [ Links ]
W3C Wiki. (2007). Math tools 2.1. 1-7. https://www.w3.org/wiki/Math_Tools [ Links ]
Wiris. (1996). MathType (Software). Recuperado em 29 novembro 2017 de: http://www.wiris.com [ Links ]
Word Wide Web Consortium. (1994). Math Tools. Recuperado em 4 de setembro 2017 de: https://www.w3.org/wiki/Math_Tools [ Links ]
Wigmore, A., Hunter, G., Pfluegel, E., & Denholm-Price, J. (2009). TalkMaths : A speech user interface for dictating mathematical expressions into electronic documents. In: 2nd ISCA Workshop of Speech and Language Technology in Education (SLaTE 2009); 3-5 Sept 2009, Wroxall, Warwickshire, U.K.
Wongkia, W., Naruedomkul, K., & Cercone, N. (2012). I-Math: Automatic math reader for Thai blind and visually impaired students. Computers and Mathematics with Applications, 64(6), 2128-2140. DOI: 10.1016/j.camwa.2012.04.009 [ Links ]
Recebido/Submission: 22/01/2020. Aceitação/Acceptance: 30/04/2020