ARTÍCULOS

Visualización de conjuntos de datos de múltiples instancias

Visualization multi-instance data sets

Jorge Eliecer Valencia-Duque ¹, Carlos Mera ², Lina Maria Sepúlveda ¹

¹ Universidad de Medellín, Medellín, 050031, Antioquia, Colombia. jeliecerv@gmail.com, lmsepulveda@itm.edu.co

² Instituto Tecnológico Metropolitano (ITM), Medellín, 050013, Antioquia, Colombia. carlosmera@itm.edu.co

---

 

RESUMEN

En el reconocimiento de patrones, los algoritmos de aprendizaje de múltiples instancias han ganado importancia puesto que evitan que el usuario tenga que delimitar, las imágenes de forma individual, para el reconocimiento de objetos. Esto supone una ventaja frente a los algoritmos de aprendizaje tradicional, puesto que disminuyen considerablemente el tiempo requerido para preparar el conjunto de datos. No obstante, una desventaja es que los conjuntos de datos resultantes suelen ser complejos, lo que dificulta su representación visual usando las técnicas tradicionales de visualización de información. Así, en este trabajo se propone una herramienta para la visualización y análisis de conjuntos de datos del paradigma de aprendizaje de múltiples instancias. La propuesta de visualización fue evaluada utilizando el criterio de expertos. Además, se realizaron diferentes pruebas que muestran que una correcta visualización puede ayudar a tomar decisiones sobre el conjunto de datos para mejorar la precisión de la clasificación.

Palabras-clave: Aprendizaje de múltiples instancias; Visualización de información; Análisis visual.

---

 

ABSTRACT

In pattern recognition, multiple-instance learning algorithms have gained importance since they avoid that the user must delimit, the images individually in order to recognize the objects. This is an advantage over traditional learning algorithms since these considerably reduce the time required to prepare the data set. However, a disadvantage is that the resulting data sets are often complex, making it difficult to visualize them using traditional information visualization techniques. Thus, this work proposes a tool for the visualization and analysis of data sets of the multi-instance learning paradigm. The visualization proposal was evaluated using the expert criteria. In addition, different tests were carried out that show that a correct visualization can help to make decisions about the data set to improve the classification precision.

Keywords: Multi-instance learning; Information visualization; Representation; Visual Analysis.

---

 

1. Introducción

El aprendizaje de múltiples instancias es un paradigma de clasificación supervisado en el que, en el contexto del reconocimiento de patrones, los objetos complejos pueden ser representados usando múltiples vectores de características (Herrera et al., 2016). Esta peculiaridad lo diferencia del aprendizaje supervisado tradicional, en el que los objetos sólo se pueden representar por un único vector de características. Así, el paradigma de aprendizaje de múltiples instancias llamado MIL por sus siglas en inglés (Multiple Instance Learning), proporciona un marco de trabajo que permite preservar mayor cantidad de información de los objetos que se desean reconocer.

Los conjuntos de datos de múltiples instancias poseen una estructura compleja donde los objetos son representados por bolsas que contienen múltiples vectores de características (llamados instancias), de ahí que se les denomine conjuntos de datos de múltiples instancias (MI). Este tipo de estructura incrementa la dificultad en la visualización del conjunto de datos, debido que además de visualizar las relaciones que existen entre las instancias individuales, se deben visualizar las relaciones que existen entre las bolsas, en otras palabras, las relaciones entre los conjuntos de instancias.

Como área de investigación la visualización de información busca el desarrollo de herramientas que ayudan a descubrir patrones ocultos en los datos, siendo un instrumento esencial para la toma de decisiones en lo que respecta a la Industria 4.0 (Arancegui & Laskurain, 2016; Janvrin, Raschke, & Dilla, 2014). En general, son diversos los campos de aplicación de la visualización de información, por ejemplo, en el análisis de datos de mercados para detectar anomalías o tendencias de mercados bursátiles (Yang, Gao, & Cao, 2013) o en el análisis de datos deportivos a fin de estimar el rendimiento de los jugadores durante un encuentro determinado (Cheplygina & Tax, 2015).

Si bien las técnicas de visualización han sido adaptadas para explorar y analizar conjuntos de datos multidimensionales tradicionales, el uso de estas técnicas es poco explorado en la representación visual de conjuntos de datos de MI. Esto se debe, como se dijo anteriormente, a la complejidad que representa su visualización. Por otra parte, son conjuntos de datos relativamente recientes y poco explorados, además que su uso aún no está generalizado entre los investigadores.

Con base en lo anterior, en este trabajo se propone una estrategia de visualización para la exploración y reducción de dimensionalidad de conjuntos de datos de MI. El resto del documento se encuentra distribuido de la siguiente forma: en la Sección 2 se presenta la fundamentación teórica del paradigma MIL y se hacen algunas consideraciones acerca de la visualización de información. En la Sección 3 se describe el desarrollo de la propuesta de visualización de conjuntos de datos de MI. En la Sección 4 se presentan los resultados internos y externos obtenidos con el método de visualización propuesto. Por último, en la Sección 5, se presentan las conclusiones y el trabajo futuro.

2. Fundamentación teórica

2.1. Aprendizaje de múltiples instancias (MIL)

En el paradigma MIL, como fue propuesto por Dietterich, Lathrop, & Lozano-Pérez (1997), un objeto es representado por una bolsa y cada instancia de la misma contiene la información extraída de una parte del objeto (Dietterich, Lathrop, & Lozano-Pérez, 1997). Formalmente, en un problema de dos clases, un conjunto de datos MI tiene la forma:

 

 

Existe un supuesto, llamado el supuesto estándar, que indica que una bolsa es positiva si al menos una de sus instancias es positiva; al contrario, una bolsa es negativa si todas sus instancias son negativas (Dietterich et al., 1997). De acuerdo con lo anterior, un clasificador MIL toma la forma de la ecuación (1).

 

 

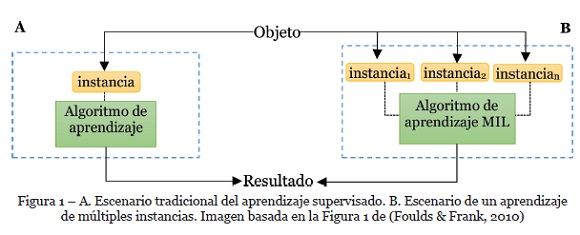
La Figura 1 ilustra la diferencia entre el aprendizaje supervisado tradicional y el aprendizaje de múltiples instancias. En el primero, un objeto se presenta por una sola instancia y en el segundo se representa por una bolsa que contiene múltiples instancias.

 

 

Con base en lo anterior, el proceso de aprendizaje de un algoritmo de clasificación en el paradigma MIL consiste en construir un modelo que a partir de un conjunto de bolsas de entrenamiento aprenda a predecir las etiquetas de clase de nuevas bolsas (Foulds & Frank, 2010). De acuerdo con Amores (Amores, 2013), los algoritmos MIL pueden ser agrupados en tres familias: basados en instancias (IS), basados en bolsas (BS) o basados en espacios embebidos o transformados (ES) (Amores, 2013; Mera et al., 2016).

La familia de algoritmos IS busca predecir las etiquetas de clase de una bolsa a partir de las etiquetas de sus instancias. Para ello, estos algoritmos consideran diferentes supuestos, siendo el supuesto estándar uno de los más utilizados (Foulds & Frank, 2010). Algunos algoritmos MIL que hacen uso de este paradigma son Multiple-Instance Support Vector Machines (MI-SVM) (Andrews, Tsochantaridis, & Hofmann, 2003) y Sparce MIL (SMIL) (Bunescu & Mooney, 2007).

Los algoritmos que pertenecen a la familia BS, toman en cuenta las bolsas como un todo y definen medidas de similitud o de distancia entre bolsas, lo que les permite definir relaciones espaciales entre bolsas y clases (Herrera et al., 2016). Además, no hay suposiciones sobre las instancias de las bolsas como sucede en IS. Usualmente, son clasificadores basados en distancias como el algoritmo de k vecinos más cercanos (k-NN), que en MIL se designa Citation k-NN (Amores, 2013; Foulds & Frank, 2010).

La familia de algoritmos ES usa funciones de transformación donde a partir de las instancias de una bolsa generan un nuevo vector de características, proyectando la bolsa a un nuevo espacio dimensional. De esta manera, un problema MIL se convierte en un problema de aprendizaje supervisado estándar (Amores, 2013). Algunos de los algoritmos MIL que emplean este paradigma son Simple-MIL que usa estadísticas de primer orden para transformar las bolsas (Mera et al., 2016); y MILES (Ma, Xu, Wu, Wang, & Chen, 2017).

2.2. Visualización de información

La visualización de información es un área de investigación que tiene como objetivo el desarrollo de herramientas que proporcionan una manera accesible de ver y comprender tendencias, valores atípicos y patrones en los datos. Lo anterior ayuda a los usuarios a explorar, entender y analizar datos a través de representaciones visuales interactivas (Liu, Cui, Wu, & Liu, 2014).

Debido al auge del análisis de grandes cantidades de datos, las herramientas que permiten gestionarlos para comprenderlos de manera profunda han ganado relevancia. Estas herramientas resultan valiosas para las empresas, debido a que permiten mejorar procesos impulsando la innovación e incrementando la productividad y los beneficios.

La visualización de información es una respuesta a una serie de retos acerca de cómo representar, interpretar y comparar datos de forma rápida y efectiva. La visualización de datos se puede presentar de diferentes maneras: estática o interactiva, dependiendo de las necesidades que se tengan, reduciendo los tiempos de respuesta a problemas puntuales (Janvrin et al., 2014).

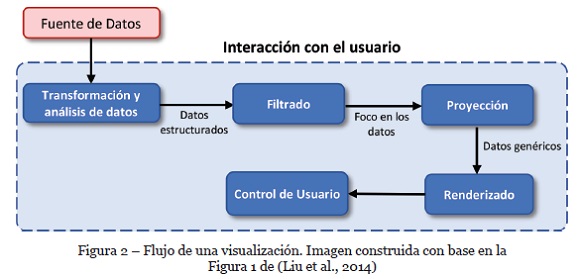
Para que los datos puedan ser visualizados, es necesario contar con un proceso que permita transformarlos en información visual para el usuario. Usualmente, este proceso se constituye en cinco etapas: transformación de datos y análisis, filtrado, proyección, representación y controles de interfaz de usuario (Liu et al., 2014), como se ilustra en la Figura 2. En este proceso, la interacción del usuario es parte fundamental en todas las etapas de una visualización, puesto que esta permite al usuario hacer una retroalimentación continua a la herramienta para lograr una visualización final de la que el usuario pueda extraer información relevante.

 

 

3. Visualización de conjuntos de datos de múltiples instancias

Las herramientas de visualización son usadas para extraer información de un conjunto de datos; sin embargo, la construcción de esas herramientas es un reto en lo que respecta a cómo representar visualmente, en un plano 2D o 3D, un conjunto de datos d-dimensional (Chan, 2006), más cuando ese conjunto de datos tiene una estructura compleja, como ocurre con los conjuntos de datos del paradigma MIL.

Por lo anterior, la visualización de un conjunto de datos de MI debe seguir un flujo que permita transformar los datos para que los métodos de visualización puedan representar la mayor cantidad de información posible. Para lograr este objetivo se utilizó como base el flujo de visualización que muestra la Figura 2. A continuación, se detalla el proceso seguido para lograr la propuesta de visualización de conjuntos de datos de MI y del desarrollo de las actividades que permitieron su construcción.

3.1. Selección de técnicas de visualización que mejor se adaptan a los conjuntos de datos de MI

Aunque la lista de métodos de visualización es bastante amplia, estos se pueden agrupar de acuerdo con su característica predominante, así:

• Proyecciones geométricas (Chan, 2006): Diagramas de dispersión (Scatterplot) (Cleveland, Mcgill, & Cleveland, 2011), Coordenadas Paralelas (Parallel Coordinates) (Inselberg, 1985)

• Técnicas orientadas a los pixeles (Pixel-Oriented Techniques) (Chan, 2006): Segmento Circular (Circle Segment) (Ankerst, Keim, & Kriegel, 1996), Gráfico de barras de pixeles (Pixel Bar Chart) (Keim & Kriegel, 1996)

• Visualización Jerárquica (Chan, 2006): Treemap (Wang, Wang, Dai, & Wang, 2006)

• Iconografía (Chan, 2006): Star Glyph (Cleveland & McGill, 1984)

Para el caso de los conjuntos de datos de MI, uno de los principales criterios para escoger un método de visualización es que este permita representar las relaciones que existen, no solo entre las instancias, sino también entre las bolsas del conjunto de datos. Otra característica deseable es que permita analizar más de una característica a la vez para poder comparar sus distribuciones y determinar cuáles pueden tener una mayor incidencia en el proceso de clasificación de las bolsas.

Basado en lo anterior, los métodos de visualización que pueden ser útiles para representar conjuntos de datos de MI son: diagramas de dispersión, gráficos de radar, gráficos de barras, mapas de calor, diagramas de red, gráficos de coordenadas paralelas y gráficos de columna radial.

3.2. Propuesta de visualización de conjuntos de datos de MI

Para iniciar con el desarrollo de la propuesta se seleccionó un grupo de conjuntos de datos de MI de prueba. Las áreas de aplicación de estos conjuntos de datos son diversas, siendo las más comunes la predicción de la actividad molecular, el etiquetado de imágenes, la categorización de texto, el reconocimiento de imágenes médicas y la clasificación de grabaciones de audio y video. Por lo anterior, los conjuntos que se usaron en la construcción de la herramienta son: Musk1 (Dietterich et al., 1997) y Fox (Andrews et al., 2003). Estos son algunos de los conjuntos de datos más empleados en el paradigma MIL.

En la literatura también se encuentran conjuntos de datos de MI artificiales construidos a partir de distribuciones Gaussianas (Carbonneau, Cheplygina, Granger, & Gagnon, 2018). Estos conjuntos artificiales ofrecen un mayor control sobre las características de los datos y permiten analizar más fácilmente el comportamiento de los algoritmos MIL y su visualización. Es por esto que se utilizó un conjunto de datos artificiales basados en Gaussianas de tres dimensiones.

Por la complejidad de los conjuntos de datos de MI se hace necesario tratar de simplificarlos sin perder información en el proceso. El uso de estrategias de reducción de la dimensionalidad permite remover las características menos relevantes en un conjunto de datos. A la vez, estas estrategias ayudan a mejorar el rendimiento de los algoritmos de clasificación y pueden incrementar la comprensión de los datos (Huang, Wu, & Ye, 2019).

Las técnicas de reducción de dimensionalidad se pueden aplicar de dos formas distintas a los conjuntos de datos de MI: sea en el espacio de las instancias o en el espacio de las bolsas. Cuando se aplica la reducción en el espacio de las instancias se omite la información de las bolsas, es decir, todo el conjunto de datos se trata como un conjunto de datos de aprendizaje supervisado tradicional en el que cada instancia hereda la etiqueta de clase de la bolsa a la que pertenece. Por otro lado, cuando se aplica la reducción de dimensiones al nivel de las bolsas, se toma cada bolsa como un conjunto de datos tradicional individual, el método considera las instancias de cada bolsa por separado y, al final, se forma un nuevo conjunto de datos con los resultados de cada subconjunto de forma independiente. De los experimentos iniciales se encontró que la reducción de dimensionalidad al nivel de las bolsas no tiene un funcionamiento adecuado debido a que se forman subconjuntos de información que, intuitivamente, parecen no guardar relación entre sí.

Las técnicas de reducción de dimensionalidad usadas en la etapa de transformación de los datos fueron: Kernel Principal Component Analysis (KPCA) (Schölkopf, Smola, & Müller, 1997), Fast Independent Component Analysis (FastICA) (Hyvärinen & Oja, 2000), Isometric Feature Mapping (Isomap) (Tenenbaum, De Silva, & Langford, 2000), Locally Linear Embedding (LLE) (Roweis & Saul, 2000), Multidimensional Scaling (MDS) (Kruskal, 1964) y T-Distributed Stochastic Neighbor Embedding (TSNE) (Maaten & Hinton, 2008).

También, se implementó una estrategia de reducción basada en Kernel Density Estimator (KDE), como se propuso en (Mera, Orozco-Alzate, & Branch, 2014). KDE es un estimador no paramétrico de densidades univariadas o multivariadas que puede ser usado para reducir el número de instancias en las bolsas, conservando las instancias más positivas y negativas (Mera et al., 2014). Otras estrategias usadas para reducir el número de instancias en las bolsas fueron los métodos estadísticos de primer orden para extraer los máximos, mínimos, promedios y extremos de cada bolsa. Estas estrategias permiten reducir el número de instancias que contiene cada bolsa y se consideró como una simplificación de esta.

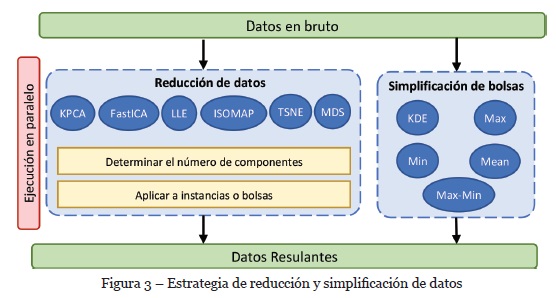
En la Figura 3 se muestra la estrategia desarrollada para transformar los datos haciendo uso de las técnicas de reducción y simplificación de bolsas. El proceso parte de un conjunto de datos de MI a partir del cual se pueden usar dos flujos, bien sea de manera independiente o combinándolos. En el caso de la reducción de datos se cuenta con la opción de elegir la cantidad de componentes (características resultantes) que se quiere obtener y se hablita la reducción en el espacio de bolsas o de instancias. Por otro lado, las técnicas de simplificación de bolsas permiten reducir el número de instancias en la bolsa. Estas se pueden aplicar posterior a una reducción de datos o de manea independiente sobre el conjunto de datos original. Al finalizar el proceso de transformación se obtiene el conjunto resultante.

 

 

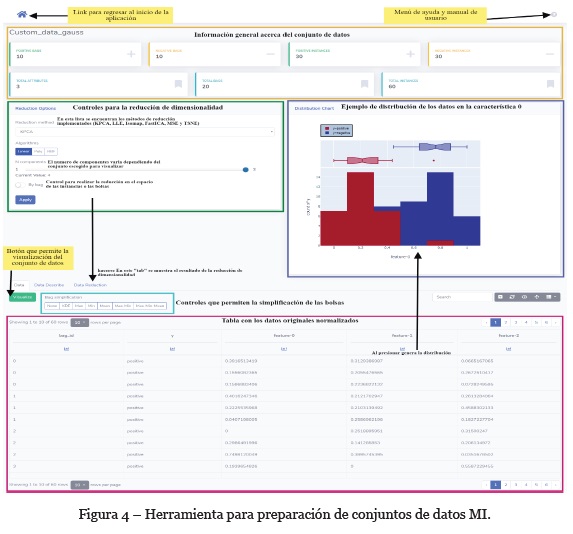
El flujo anterior se integró a una aplicación web. Como se muestra en la Figura 4, los controles implementados tienen los métodos de reducción y simplificación mencionados. Además, se agregaron controles extra para la manipulación de los datos originales y los datos resultantes después de la reducción.

 

 

Para permitir al usuario analizar los conjuntos de datos de MI, se agregó un gráfico que muestra la distribución de las instancias negativas y positivas de cada una de las dimensiones del conjunto de datos resultante.

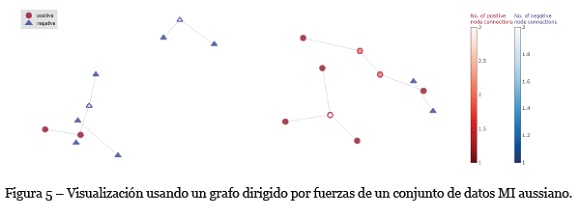
Para efectos de un análisis visual del conjunto de datos se propone el uso de dos gráficos. El primero permite visualizar las relaciones entre las bolsas y es un grafo dirigido por fuerzas con dos tipos de nodos: los círculos rojos, que representa las bolsas positivas y los triángulos azules que representan las bolsas negativas (Figura 5). El tamaño de cada nodo está definido con base en la cantidad de instancias, así entre más instancias tiene una bolsa, mayor es el tamaño de la figura que la representa. En el lateral de la visualización se dispusieron dos barras que indican el número de conexiones de las bolsas positivas y negativas en una escala de intensidad por color. Como elemento de interacción se implementaron diferentes algoritmos que cambian la disposición de los nodos del grafo.

 

 

Por defecto, en la visualización se usa el algoritmo Fruchterman-Reingold force-directed (spring), el cual busca minimizar la energía del sistema moviendo los nodos y cambiando las fuerzas entre dos nodos cualquiera. En este sentido, la suma de los vectores de fuerza determina en qué dirección debe moverse un nodo para posicionarlo automáticamente de manera que se minimice la energía total del sistema. El grafo se estabiliza cuando el sistema alcanza su estado de equilibrio, es decir cuando se minimiza por completo la energía del sistema (Kobourov, 2012).

Como el peso de los vértices está definido con base en la distancia entre las bolsas, y dicha distancia se calcula con base en las instancias entre las bolsas (Amores, 2013), entonces se puede escoger si el peso de un vértice se asigna con base en la distancia mínima, máxima o la media entre las distancias de las instancias en dos bolsas. Por otro lado, la métrica de distancia usada es la distancia Euclidiana, aunque se tienen implementados diferentes métricas en caso de que el usuario considere más conveniente usar otra. Algunas de estas son: braycurtis, chebyshev, correlation, euclidean, haming y mahalanobis.

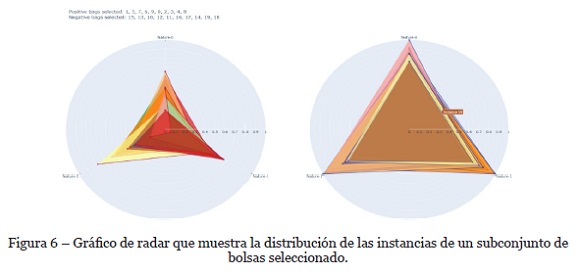
El segundo gráfico de la propuesta de visualización corresponde a dos diagramas de radar. Uno para visualizar las instancias de las bolsas positivas y otro para visualizar las instancias de las bolsas negativas. Cada uno de estos diagramas muestra la distribución de las instancias respecto a las características seleccionadas. En la Figura 6 se puede observar la representación de un conjunto Gaussiano, en el cual se observa que las características de las instancias de las bolsas negativas (derecha) tienen valores cercanos a uno; cabe aclarar que esos valores están normalizados para una representación uniforme entre los diferentes conjuntos de datos. Respecto a las instancias de las bolsas positivas (izquierda) el gráfico permite identificar que algunas de las instancias tienen valores cercanos a uno en sus características (al igual que las instancias de las bolsas negativas); esto sugiere que dichas instancias pueden ser negativa y se consideran instancias ruidosas en las bolsas positivas.

 

 

Los gráficos propuestos permiten, rápidamente, determinar qué características son predominantes entre las instancias, lo que es útil para determinar qué atributos pueden tener mayor influencia en la definición y la distinción entre las bolsas positivas y las negativas. No obstante, una de las debilidades de esta representación se presenta cuando se seleccionan bolsas con demasiadas instancias, puesto que por la naturaleza del gráfico este se torna más difícil de leer conforme aumenta el número de instancias.

3.3. Evaluación de la técnica de visualización propuesta

Para evaluar la propuesta de visualización se realizaron dos tipos de validaciones, una externa y otra interna. La externa fue realizada por expertos en el paradigma MIL que evaluaron desde dos puntos de vista la herramienta. El primero se centró en la usabilidad y el segundo se enfocó en la utilidad de la herramienta. En la evaluación interna se valoró si las transformaciones realizadas a los conjuntos de datos mejoraban la precisión de un clasificador MIL. Los resultados de estas evaluaciones se presentan en la Sección 4.

4. Resultados

4.1. Resultados de la evaluación interna

Esta evaluación se enfocó en valorar si existe alguna mejora en la comprensión del conjunto de datos midiendo el impacto de las transformaciones que realiza el usuario sobre el desempeño de un clasificador MIL. Específicamente, se utilizó el algoritmo SimpleMIL el cual pertenece a la categoría de espacios embebidos para transformar el problema de clasificación MIL a un problema de clasificación tradicional (Foulds & Frank, 2010). Para ello, las instancias de cada bolsa se embebieron a un nuevo espacio de características aplicando las funciones mínimo, máximo, promedio y extremos, entre las instancias de cada bolsa.

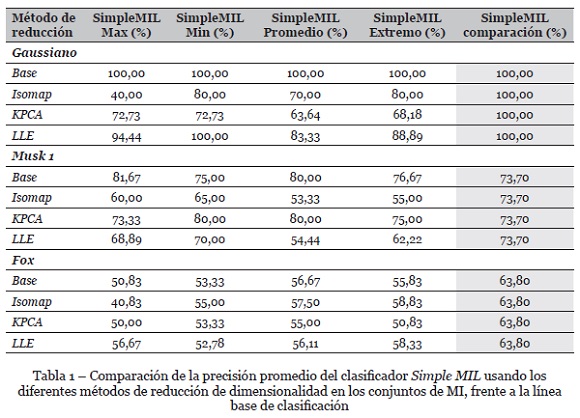
También se utilizaron tres métodos de reducción de dimensionalidad: KPCA (con un kernel lineal), Isomap y LLE. Igualmente, se aplicó un método para la reducción de instancias, considerando la instancia más positiva y más negativa calculadas a partir de la estimación de densidad de la clase negativa con KDE. Las pruebas se hicieron sobre los conjuntos de datos Musk1, Fox y el conjunto de datos artificiales basado en Gaussianas. La Tabla 1 resume los resultados de clasificación sobre estos conjuntos de datos en términos de precisión usando una partición 80/20 para entrenamiento y validación respectivamente.

 

 

Los resultados arrojados permitieron ver que en algunos casos se puede mejorar la clasificación si los atributos excluidos son los adecuados; en caso contrario la precisión del algoritmo disminuye. Esto se evidencia para los tres conjuntos usados, sin embargo, es más notorio en Musk 1 y Fox que en el Gaussiano.

La exclusión de ciertas características en el conjunto de datos se hizo con base en la visualización de cada conjunto de datos. Para ello, se utilizó la visualización basada en grafos, la cual permitió detectar los grupos de bolsas que estaban relacionadas, de acuerdo con una métrica de distancia. A partir del grafo, se seleccionaron aquellas bolsas positivas y negativas que se encuentran conectadas y cercanas unas a otras.

Las bolsas seleccionadas fueron proyectadas usando el gráfico de radar el cual permitió identificar las características con valores predominantemente altos entre las instancias del conjunto de datos. Al retirar esas características se creó un subconjunto con las características de valores bajos con el que se entrenó el clasificador SimpleMIL.

Al realizar el procedimiento descrito, se encontró que al retirar las características que tienen valores altos es posible obtener una mejora leve en la precisión del algoritmo. Por el contrario, si se retiran las características con valores bajos, la precisión del algoritmo tiende a bajar. La mejora y la disminución en la precisión en cualquier caso está en un rango de 0 a 10 puntos, no obstante, esto depende del conjunto de datos usado. En las pruebas se observó que la precisión tiende a mejorar más en los conjuntos de datos de MI de problemas reales, mientras que para el conjunto de los datos Gaussianos no suele haber mejoras significativas.

En la Tabla 1 se muestra cómo varía la precisión promedio del clasificador Simple MIL cuando se aplican los métodos de reducción de dimensionalidad comparado con la línea base de referencia^[1]. Para el conjunto de datos Gaussianos, no es muy eficiente aplicar métodos de reducción, en especial Isomap y KPCA, que arrojan una precisión baja en comparación con los valores de referencia de la última columna y la primera fila. En cuanto a los conjuntos de datos Musk1 y Fox los métodos de reducción son un poco más efectivos, aunque no siempre es así con las diferentes variaciones del algoritmo de clasificación. En Musk1 KPCA es el método con mejores resultados, mientras en Fox LLE e Isomap muestran resultados satisfactorios.

4.2. Resultados de la evaluación externa

Para esta evaluación se solicitó a los expertos en MIL que realizaran una valoración sobre la usabilidad y el funcionamiento de la herramienta. Para ello se realizó una encuesta con 7 preguntas las cuales buscaban comprender mejor lo que los expertos opinaban acerca de la aplicación. En la evaluación de usabilidad se trataron de valorar de manera objetiva 10 apartados: características y funcionalidad, página de inicio, navegación, búsquedas, controles y retroalimentación, formularios, errores, contenido y texto, ayudas y rendimiento. Esta evaluación se basó en los 45 principios de usabilidad de mejores prácticas descritos en (Turner, 2011).

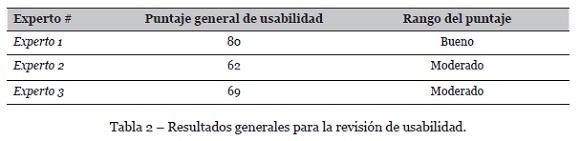
En la Tabla 2 se muestran las puntaciones resultantes de cada experto sobre la usabilidad de la herramienta, dejando claro que esta aún debe mejorarse, bien sea creando instructivos más fáciles de entender o proporcionando herramientas de ayuda que guíen al usuario durante el flujo de la visualización.

 

 

A continuación, se presentan algunas de las respuestas más relevantes que se obtuvieron en la encuesta realizada. No se muestran todas debido a que con estas opiniones es suficiente para hacerse una idea acerca de la propuesta de visualización.

Encuesta

¿Considera herramientas como esta útiles para el proceso de toma de decisiones en el paradigma de aprendizaje de múltiples instancias (MIL)?

“Claro, siempre será importante la exploración inicial y visualización de los datos. Herramientas como esta ayudan a tener una idea general de nuestros datos y a realizar transformaciones que son muy útiles en el aprendizaje de MIL.”

¿Los datos mostrados son precisos y útiles para el entendimiento en general del conjunto de datos de MI?

“Si, pero falta mayor información descriptiva y visual acerca de los datos…”

¿La visualización responde claramente las preguntas planteadas inicialmente o plantea nuevas preguntas sobre los datos?

“Las visualizaciones no me parecieron claras. Es necesario acompañar las gráficas en la interfaz con texto adicional que facilite su interpretación…”

En resumen y con base en las respuestas dadas por los expertos a la encuesta realizada, se puede deducir que aún hay un camino de mejoras que se deben hacer en la visualización de conjuntos de datos de MI, esto muestra también que esta primera aproximación es una buena idea y un campo de investigación que podría ser de ayuda significante en la exploración de conjuntos de datos complejos y ayudaría en un entendimiento mejor de los conjuntos de MI y los algoritmos MIL para su clasificación.

5. Conclusiones y trabajo futuro

La comparación de los diferentes métodos de visualización y la caracterización de los conjuntos de datos de MI permitió encontrar formas de representar estos datos y extraer información relevante para mejorar la precisión en el entrenamiento de un algoritmo MIL. Además, posibilitó el desarrollo de una herramienta de visualización que, pese a sus debilidades, puede ser de utilidad a los investigadores del área.

También se ha podido concluir que la reducción en conjuntos de datos de MI de pocas dimensiones puede resultar contraproducente en la clasificación, también que no todos los métodos de reducción de datos son efectivos o funcionan de igual manera en los diferentes tipos de conjuntos de datos de MI. Esto plantea algunas incógnitas, en especial las relacionadas con qué métodos de reducción podrían resultar más efectivos en conjuntos de datos de múltiples instancias.

Como trabajo futuro, se tiene planeado hacer esfuerzos en encontrar otros métodos de visualización que representen la estructura y las relaciones de los datos de mejor manera, además de profundizar más en las particularidades de la estructura de los conjuntos de datos de MI. Esto si se quiere tener un aporte más significativo a la industria 4.0 y ayudar de forma más profunda a la toma de decisiones. Por otro lado, en siguientes versiones de la herramienta se deben las interacciones necesarias para modificar los parámetros de los métodos de reducción. También se deben agregar y evaluar otros métodos de reducción como Uniform Manifold Approximation and Projection (UMAP).

Para finalizar, se comprobó que dependiendo del conjunto de datos usado la representación puede verse afectada, por lo que sería conveniente crear métodos que se adapten al tipo o estructura del conjunto de datos de MI y de esta forma obtener mejores resultados.

 

REFERENCIAS

Amores, J. (2013). Multiple instance classification: Review, taxonomy and comparative study. Artificial Intelligence, 201, 81-105.         [ Links ]

Andrews, S., Tsochantaridis, I., & Hofmann, T. (2003). Support vector machines for multiple-instance learning. In Advances in neural information processing systems (pp. 577-584).         [ Links ]

Ankerst, M., Keim, D., & Kriegel, H. (1996). “Circle Segments”: A Technique for Visually Exploring Large Multidimensional Data Sets. In Proc. IEEE Visualization ’96, Hot Topic Session (pp. 5-8). http://nbn-resolving.de/urn:nbn:de:bsz:352-opus-70761        [ Links ]

Arancegui, M. N., & Laskurain, X. S. (2016). Reflexiones sobre la Industria 4.0 desde el caso vasco. EKONOMIAZ. Revista Vasca de Economía, 89(01), 142-173. https://ideas.repec.org/a/ekz/ekonoz/2016106.html        [ Links ]

Bunescu, R. C., & Mooney, R. J. (2007). Multiple instance learning for sparse positive bags. In Proceedings of the 24th international conference on Machine learning (pp. 105-112).         [ Links ]

Carbonneau, M. A., Cheplygina, V., Granger, E., & Gagnon, G. (2018). Multiple instance learning: A survey of problem characteristics and applications. Pattern Recognition, 77, 329-353. https://doi.org/10.1016/j.patcog.2017.10.009        [ Links ]

Chan, W. W.-Y. (2006). A survey on multivariate data visualization. Department of Computer Science and Engineering. Hong Kong University of Science and Technology, 8(6), 1-29.         [ Links ]

Cheplygina, V., & Tax, D. M. J. (2015). Characterizing multiple instance datasets. In International Workshop on Similarity-Based Pattern Recognition (pp. 15-27).         [ Links ]

Cleveland, W. S., & McGill, R. (1984). Graphical perception: Theory, experimentation, and application to the development of graphical methods. Journal of the American Statistical Association, 79(387), 531-554. https://doi.org/10.1080/01621459.1984.10478080        [ Links ]

Cleveland, W. S., Mcgill, R., & Cleveland, S. (2011). The Many Faces of a Scafferplot. Faces, 79(388), 807-822.         [ Links ]

Dietterich, T. G., Lathrop, R. H., & Lozano-Pérez, T. (1997). Solving the multiple instance problem with axis-parallel rectangles. Artificial Intelligence, 89(1-2), 31-71. https://doi.org/10.1016/s0004-3702(96)00034-3        [ Links ]

Foulds, J. R., & Frank, E. (2010). A review of multi-instance learning assumptions. Knowledge Engineering Review, 25(1), 1-25.         [ Links ]

Herrera, F., Ventura, S., Bello, R., Cornelis, C., Zafra, A., Sánchez-Tarragó, D., & Vluymans, S. (2016). Multiple instance learning: Foundations and algorithms. In Multiple Instance Learning: Foundations and Algorithms. Springer International Publishing. https://doi.org/10.1007/978-3-319-47759-6        [ Links ]

Huang, X., Wu, L., & Ye, Y. (2019). A Review on Dimensionality Reduction Techniques. International Journal of Pattern Recognition and Artificial Intelligence, 33(10), 975-8887. https://doi.org/10.1142/S0218001419500174        [ Links ]

Hyvärinen, A., & Oja, E. (2000). Independent component analysis: algorithms and applications. Neural Networks : The Official Journal of the International Neural Network Society, 13(4-5), 411-430. https://doi.org/10.1016/s0893-6080(00)00026-5        [ Links ]

Inselberg, A. (1985). The plane with parallel coordinates. The Visual Computer, 1(4), 69-91. https://doi.org/10.1007/BF01898350        [ Links ]

Janvrin, D. J., Raschke, R. L., & Dilla, W. N. (2014). Making sense of complex data using interactive data visualization. Journal of Accounting Education, 32(4), 31-48. https://doi.org/10.1016/j.jaccedu.2014.09.003        [ Links ]

Keim, D. A., & Kriegel, H. P. (1996). Visualization techniques for mining large databases: A comparison. IEEE Transactions on Knowledge and Data Engineering, 8(6), 923-938. https://doi.org/10.1109/69.553159        [ Links ]

Kobourov, S. G. (2012). Spring Embedders and Force Directed Graph Drawing Algorithms. http://arxiv.org/abs/1201.3011        [ Links ]

Kruskal, J. B. (1964). Nonmetric multidimensional scaling: A numerical method. Psychometrika, 29(2), 115-129. https://doi.org/10.1007/BF02289694        [ Links ]

Liu, S., Cui, W., Wu, Y., & Liu, M. (2014). A survey on information visualization: recent advances and challenges. The Visual Computer, 30(12), 1373-1393. https://doi.org/10.1007/s00371-013-0892-3        [ Links ]

Ma, Y., Xu, J., Wu, X., Wang, F., & Chen, W. (2017). A visual analytical approach for transfer learning in classification. Information Sciences, 390, 54-69.         [ Links ]

Maaten, L. van der, & Hinton, G. (2008). Visualizing data using t-SNE. Journal of Machine Learning Research, 9(Nov), 2579-2605.         [ Links ]

Mera, C., Orozco-Alzate, M., & Branch, J. (2014). Improving Representation of the Positive Class in Imbalanced Multiple-Instance Learning. In Lecture Notes in Computer Science (including subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics) (Vol. 8814, pp. 266-273). Springer Verlag. https://doi.org/10.1007/978-3-319-11758-4_29        [ Links ]

Mera, C., Orozco-Alzate, M., Branch, J., & Mery, D. (2016). Automatic visual inspection: An approach with multi-instance learning. Computers in Industry, 83, 46-54. https://doi.org/10.1016/j.compind.2016.09.002        [ Links ]

Roweis, S. T., & Saul, L. K. (2000). Nonlinear dimensionality reduction by locally linear embedding. Science, 290(5500), 2323-2326. https://doi.org/10.1126/science.290.5500.2323        [ Links ]

Schölkopf, B., Smola, A., & Müller, K.-R. (1997). Kernel principal component analysis. In International conference on artificial neural networks (pp. 583-588).         [ Links ]

Tenenbaum, J. B., De Silva, V., & Langford, J. C. (2000). A global geometric framework for nonlinear dimensionality reduction. Science, 290(5500), 2319-2323. https://doi.org/10.1126/science.290.5500.2319        [ Links ]

Turner, N. (2011). A guide to carrying out usability reviews . Retrieved July 14, 2020, from http://www.uxforthemasses.com/usability-reviews/        [ Links ]

Wang, W., Wang, H., Dai, G., & Wang, H. (2006). Visualization of large hierarchical data by circle packing. In Proceedings of the SIGCHI conference on Human Factors in computing systems - CHI ’06 (Vol. 1, p. 517). ACM Press. https://doi.org/10.1145/1124772.1124851        [ Links ]

Weidmann, N., Frank, E., & Pfahringer, B. (2003). A two-level learning method for generalized multi-instance problems. In European Conference on Machine Learning (pp. 468-479).         [ Links ]

Yang, W., Gao, Y., & Cao, L. (2013). TRASMIL: A local anomaly detection framework based on trajectory segmentation and multi-instance learning. Computer Vision and Image Understanding, 117(10), 1273-1286. https://doi.org/10.1016/j.cviu.2012.08.010        [ Links ]

 

Recebido/Submission: 02/05/2020. Aceitação/Acceptance: 16/08/2020

 

^[1]Valores de comparación extraídos de http://homepage.tudelft.nl/n9d04/milweb/index.html