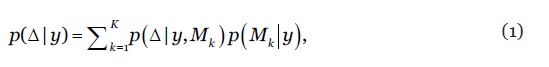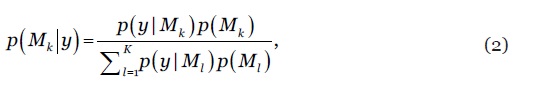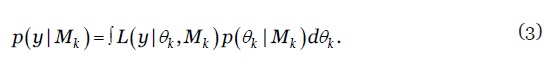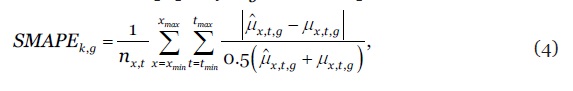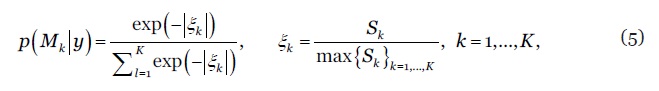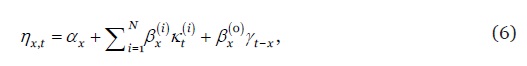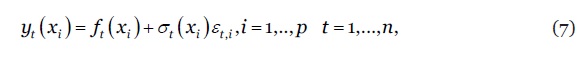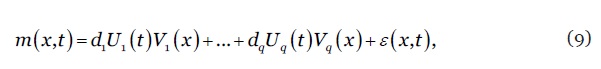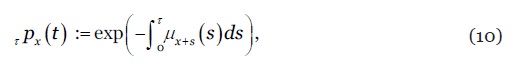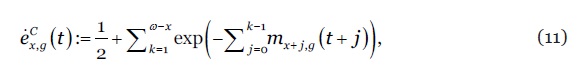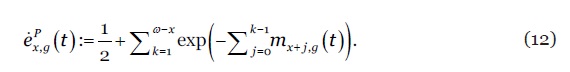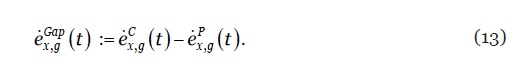1. Introdução
A evolução da longevidade humana nos países desenvolvidos nas últimas décadas é marcada por um aumento notável da esperança de vida em todas as idades, fruto da redução das taxas de mortalidade em todo o arco da vida humana, resultado da melhoria das condições de vida e de avanços substanciais no tratamento e cura de algumas das principais causas de morte. Esta redução não é homogénea quando considerada por grupos socioeconómicos assumindo, regra geral, uma correlação positiva com o nível de rendimento, riqueza e qualificação dos indivíduos, e apresenta diferenças entre sexos (NASEM, 2015; Ayuso, Bravo e Holzmann, 2017a; Ayuso, Bravo e Holzmann 2017b). Estes ganhos de longevidade constituem, naturalmente, uma alteração positiva para os indivíduos e uma significativa conquista civilizacional das sociedades modernas, mas colocam novos e importantes desafios em múltiplas áreas de intervenção pública e privada como, por exemplo, a sustentabilidade dos sistemas públicos de saúde e de protecção social, a educação ao longo da vida, o planeamento do território, as políticas de habitação e de segurança (Bravo, 2016). As projecções de mortalidade são usadas por organismos oficiais de estatística na produção de projecções de população residente determinando, em conjunto com os fluxos migratórios internacionais e a fecundidade, a dinâmica do efectivo populacional e a sua distribuição por idade e sexo (Bravo & Coelho, 2019).
As projecções de mortalidade e de esperança de vida são um elemento essencial na avaliação e na gestão do risco em seguros do ramo vida (e.g., rendas vitalícias) e em planos e fundos de pensões, sejam eles públicos ou privados, dada a natureza de muito longo prazo dos compromissos assumidos e o actual contexto de taxas de juro baixas ou negativas (Bravo e El Mekkaoui de Freitas, 2018; Blake et al, 2019; Bravo, 2020; Bravo, 2019), no pricing de soluções de mobilização da riqueza imobiliária (equity release schemes) e na avaliação de instrumentos de mercado de capitais para a cobertura dos riscos de longevidade e de mortalidade, por exemplo, longevity bonds, q-forwards, longevity swaps/options (Bravo & Nunes, 2021).
Um denominador comum nas reformas realizadas nos sistemas de pensões da OCDE para responder ao aumento da esperança de vida e ao envelhecimento da população tem sido a criação de mecanismos automáticos de indexação das pensões à esperança de vida (OCDE, 2017). A criação de factores de sustentabilidade (e.g., Portugal, Espanha), a indexação automática da idade de reforma à esperança de vida (e.g., Dinamarca, Portugal), a indexação das condições de acesso às prestações, a fixação de bonificações (penalizações) por reforma postecipada (antecipada) (e.g., Portugal), a introdução de estabilizadores automáticos (e.g., Suécia), são apenas alguns exemplos desta tendência. Esta opção política socorreu-se, contudo, de uma medida errada da longevidade humana, a esperança de vida por período, uma métrica que assume que as condições de mortalidade são estáticas, em detrimento de uma estimativa mais aproximada da vida residual dos indivíduos representada pela esperança de vida por coorte, que incorpora a dinâmica esperada das probabilidades de sobrevivência da população (Ayuso, Bravo e Holzmann, 2020). O cálculo da esperança de vida por coorte pressupõe a utilização de métodos estocásticos de projecção das taxas de mortalidade específicas por idade e sexo. Na literatura demográfica e actuarial, são inúmeros os modelos propostos para este fim agrupados, regra geral, em métodos de natureza paramétrica, principal component methods, e métodos de graduação (Lee e Carter, 1992; Brouhns et al, 2002; Renshaw e Haberman, 2006; Currie, 2006; Cairns et al, 2006; Cairns et al, 2009; Hyndman e Ullah, 2007; Plat, 2009; Hunt e Blake, 2020). Estas projecções não estão isentas dos riscos de modelo e de estimação dos parâmetros.
Neste artigo seguimos (Bravo, Ayuso, Holzmann e Palmer, 2020) e ensaiamos a aplicação à população portuguesa em idade adulta de uma abordagem inovadora em estudos demográficos e actuariais que envolvem modelos competitivos assente numa combinação Bayesiana de modelos (Bayesian Model Ensemble, BME) heterogéneos. Quando comparada com abordagens assentes em modelo único, a abordagem BME demonstrou em variados estudos empíricos um poder preditivo superior aos métodos de machine learning, com a vantagem de que reduz o risco de modelo e diversifica as covariáveis usadas na projecção. A combinação usada no estudo inclui nove modelos candidatos, seis dos quais modelos generalizados idade-periodo-coorte, o método de séries temporais de Hyndman e Ullah ponderado, um modelo assente na análise de componentes principais regularizada, e a técnica de P-Splines bidimensional com penalização. Os modelos são calibrados à população portuguesa desagregada por sexo usando informação estatística obtida da (Human Mortality Database, 2020) relativa ao período 1960-2018 e às idades adultas no intervalo 60-125. A escolha particular deste intervalo de idades prende-se com a sua relevância para a análise da sustentabilidade dos sistemas públicos e privados de protecção social e de saúde em Portugal. São ainda calculados intervalos de confiança para a combinação de modelos usando a metodologia Model-Averaged Tail Area (MATA). O estudo apresenta e analisa os resultados da aplicação da metodologia à população portuguesa e discute as suas implicações nalgumas áreas de intervenção. O resto do artigo está organizado da seguinte forma. Na Secção 2 é apresentada a metodologia usada no estudo e os procedimentos adoptados para a sua implementação. Na Secção 3 são apresentados e discutidos os principais resultados para a evolução projectada da mortalidade e da esperança de vida em Portugal. A Secção 4 resume as principais conclusões e contributos da investigação.
2. Metodologia
2.1. Combinação Bayesiana de modelos
A metodologia tradicional de projecção da mortalidade envolve a utilização de um único modelo seleccionado de um conjunto restrito de alternativas, usando um método ou um critério (e.g., BIC, AIC, métrica de avaliação do poder preditivo, testes de hipóteses para selecção de modelos encaixados, cross-validation, bootstrapping), frequentemente sem considerar o risco de modelo. O método seleccionado é então considerado como o «verdadeiro» (o melhor) para efeitos de inferência estatística, uma escolha que implicitamente limita (reduz) a incerteza na projecção uma vez que ignora o risco de modelo. Para contornar esta limitação, neste artigo acompanhamos (Bravo et al, 2020) e usamos uma abordagem alternativa baseada numa combinação adaptativa de modelos heterogéneos que inclui seis modelos generalizados idade-periodo-cohorte (Generalised Age-Period-Cohort (GAPC) models), o método de séries temporais de Hyndman e Ullah ponderado (Shang et al, 2011), um modelo assente numa análise de componentes principais regularizada (Regularized Singular Value Decomposition, RSVD) e a técnica de P-splines bidimensional (two-dimensional smooth constrained P-splines).
A combinação de modelos consiste na aplicação da teoria Bayesiana à selecção de modelos e à inferência estatística em contexto de incerteza quanto ao melhor modelo. A combinação adaptativa adoptada neste artigo é inspirada no conceito de model confidence set proposto por (Hansen et al, 2011) e usado, por exemplo, por (Samuels e Sekkel, 2017) e (Bravo et al, 2020). O pressuposto é o de que a combinação de modelos deve ser precedida de uma selecção prévia de um subconjunto de melhores modelos, usando para tal um critério de escolha (e.g., poder preditivo do modelo). Designemos por os modelos candidatos, representando o conjunto de distribuições de probabilidade (PDF) que compreendem a função de verosimilhança dos dados observados em termos dos parâmetros específicos de cada modelo e um conjunto de funções de densidade de probabilidade prévias Seja a variável de interesse presente em todos os modelos, por exemplo, o valor futuro de . Segundo a lei de probabilidade total, a distribuição marginal posterior da variável de interesse considerando os modelos é definida por
onde designa a distribuição de probabilidade projectada de com base no modelo e representa a probabilidade posterior do modelo estimada a partir dos dados (lookforward window), ou seja, espelhando a sua aderência aos dados ou o seu poder preditivo. A distribuição à posteriori do modelo é dada por
onde
As probabilidades à posteriori dos modelos totalizam a unidade, i.e., e podem ser interpretadas como ponderadores (pesos). A distribuição de probabilidade da combinação de modelos BME é assim uma média ponderada das PDF dos modelos individuais, em que os ponderadores são as suas probabilidades à posteriori (Raftery et al., 2005). Para identificar os modelos que integram o model confidence set e respectivos ponderadores na BME, para cada uma das três subpopulações os modelos são, numa primeira fase, estimados na amostra de treino (training set) e posteriormente hierarquizados segundo o seu poder preditivo na amostra de teste (out-of-sample test set). Foram consideradas diferentes métricas de avaliação do poder preditivo (MAPE, RMSE, SMAPE, SSE, etc.) optando-se, finalmente, pelo indicador Symmetric Mean Absolute Percentage Error (SMAPE) para o cálculo dos ponderadores, uma variante do erro percentual médio bastante usada em competições internacionais de modelos de previsão. O SMAPE do modelo e subpopulação é definido por
onde e denotam, respectivamente, as estimativas pontuais e os valores observados das taxas de mortalidade, , , , , . As amostras de treino e de teste são definidas de modo a permitir um horizonte de previsão de 5 anos em todos os modelos e subpopulações. Os dados estatísticos sobre a mortalidade e a exposição ao risco foram extraídos do repositório internacional (Human Mortality Database (2020). O computo das probabilidades à posteriori dos modelos socorre-se da função exponencial normalizada (também conhecida por função softmax ou softargmax), definida por
onde simboliza o valor da métrica SMAPE do modelo Esta função atribui um peso maior aos modelos com melhor desempenho preditivo, seguindo os pesos uma função exponencial. Identificado o model confidence set e calculado o seu peso relativo, da aplicação da equação (1) obtemos uma combinação probabilística de taxas de mortalidade, com base nas quais se calculam as esperanças de vida por período e coorte. A derivação de intervalos de confiança para a combinação de modelos socorre-se da metodologia Model-Averaged Tail Area (MATA) desenvolvida por (Turek and Fletcher, 2012), assente numa média ponderada de intervalos de credibilidade Bayesianos.
2.2. Modelos estocásticos de projecção da mortalidade
A Tabela 1 resume os nove modelos estocásticos de projecção da mortalidade usados neste estudo, escolhidos com base no seu desempenho empírico em estudos similares (Cairns et al., 2009; Dowd et al, 2010; Bravo et al, 2020). O conjunto base compreende seis modelos do tipo GAPC, modelos paramétricos da classe dos modelos lineares generalizados (GLM) que vinculam a variável de resposta a um previsor linear ou bilinear que inclui, como variáveis explicativas, a idade do indivíduo, , o tempo cronológico e a geração (ano) de nascimento (ou coorte), , a que acrescem restrições de identificação dos modelos, uma função link e métodos univariados de séries para obter projecções (Hunt e Blake, 2020). A componente aleatória dos modelos assume que o número de óbitos à idade no ano segue uma distribuição de Poisson com ou uma distribuição Binomial com onde e denotam, respectivamente, a população inicialmente ou centralmente exposta ao risco, e e denotam a taxa de mortalidade e a probabilidade de morte à idade no ano . A componente sistemática do modelo liga a variável de resposta ( ou ) a um determinado previsor linear
onde representa a configuração geral da mortalidade por idade, refere um conjunto de termos idade-período que descrevem as tendências globais na mortalidade, sendo um índice temporal e um parâmetro de sensibilidade por idade, e o termo compreende os efeitos geracionais, sendo um parâmetro modulador por idade. Os índices temporais e geracionais são processos estocásticos, modelados através de métodos univariados de séries temporais ARIMA(p,d,q) usando a metodologia de Box-Jenkins.
Tabela 1 Modelos estocásticos de projecção da mortalidade

(Brouhns et al. 2002; Currie 2006; Renshaw e Haberman 2006; Cairns et al 2006; Cairns et al. 2009; Plat 2009; Shang et al.2011; Camarda 2019; Huang et al. 2009)
Fonte: Elaboração própria.
O subconjunto de modelos GAPC usados neste estudo compreende: [LC] o modelo Poisson-Lee-Carter (Brouhns et al., 2002); [APC] o modelo idade-período-coorte de (Currie 2006); [RH] a extensão do modelo de Lee-Carter incluindo efeitos coorte e (Renshaw e Haberman, 2006); [CBD] o modelo Cairns-Blake-Dowd com e onde denota a idade média na amostra (Cairns et al, 2006); [M7] a extensão do modelo CBD incluindo efeitos coorte (Cairns et al., 2009); [Plat] o modelo de Plat (2009) com . Os parâmetros são estimados usando métodos de máxima-verosimilhança. O fecho das tábuas de mortalidade à idade limite socorre-se do método de (Denuit e Goderniaux, 2005). Alguns dos modelos GAPC descritos na Tabela 1 são casos particulares de modelos mais gerais. Por exemplo, o modelo LC é encaixado no modelo RH assumindo , e sendo igualmente um caso particular do modelo APC com e sem efeitos coorte. A metodologia BME usada neste estudo selecciona, em cada população, o subconjunto de modelos GAPC encaixados que apresenta melhor desempenho preditivo e exclui do model confidence set os restantes (três dos seis candidatos) usando uma fixed-rule trimming scheme. Para cada modelo individual, são usados métodos de bootstrap semi-paramétricos para derivar intervalos de confiança para as variáveis de interesse considerando um total de 10000 simulações (Brouhns et al., 2005).
O leque de métodos de projecção da mortalidade usados no estudo compreende ainda o modelo demográfico funcional (Functional Demographic Model (FDM)) assente numa análise de componentes principais desenvolvido originalmente por (Hyndman e Ullah, 2007) e expandido por (Shang et al, 2011). Formalmente,
onde , são funções contínuas e suaves da idade, é um parâmetro de volatilidade ajustável com a idade e período , e é um ruído branco. Este estudo considera ainda a técnica de P-Splines bidimensional com penalização proposta por (Camarda, 2019), descrita formalmente pela matriz de regressão
onde é um vector de parâmetros e designa o produto de Kronecker de bases B-splines igualmente espaçadas para a idade e ano , complementadas com uma penalização bidimensional e restrições de modo a assegurar projecções biologicamente plausíveis para a mortalidade. Por fim, o estudo inclui ainda a abordagem bidimensional (por idade e período) assente na análise de componentes principais regularizada proposta por (Huang et al, 2009). Em termos formais, os autores assumem que
onde designa a taxa de mortalidade, o valor próprio, e são funções suaves da idade e período, respectivamente, e um ruído branco. Para obter projecções e intervalos de confiança, as funções são modeladas como séries temporais usando processos estocásticos do tipo ARIMA. As tarefas de estimação, simulação e projecção dos modelos e aplicação da abordagem BME foram concretizadas com recurso a uma rotina informática escrita em software R.
2.3. Cálculo da Esperança de Vida
Seja a probabilidade de sobrevivência -anos de um indivíduo à idade no ano
onde denota a intensidade de mortalidade estocástica. Na discretização do processo estocástico, assumimos que é constante no interior de cada quadrado do diagrama de Lexis. Formalmente, para e números inteiros, assume-se que para , donde decorre que: (i) é estimada pela taxa central de mortalidade , (ii) a probabilidade anual de sobrevivência é dada por A esperança de vida por coorte de um indivíduo com idade no ano , pertencente à população , é dada por
enquanto que a respectiva esperança de vida por período é calculada segundo
O conceito de gap de esperança de vida (life expectancy gap), , corresponde à diferença sistemática entre a esperança de vida por coorte e período (Ayuso et al., 2020). O seu valor expressa uma estimativa dos anos de vida adicionais (a menos) que uma determinada geração usufruirá em resultado dos ganhos (perdas) de longevidade esperados. Um valor positivo (negativo) sinaliza um aumento (redução) esperado da esperança de vida para uma dada geração. O seu valor é calculado mediante
3. Análise e Discussão dos Resultados
3.1. Definição do model confidence set e ponderadores
A Figura 1 representa, para os nove modelos candidatos, as curvas de mortalidade ajustadas no intervalo de idades 60-95 e training set (período 1960-2013) considerando o conjunto da população portuguesa. Como se observa, o normal aumento da mortalidade com a idade antecipado nestas idades e a dinâmica multidimensional de aumento continuado da longevidade são captados de forma distinta pelos diferentes métodos usados, constatando-se, por exemplo, que alguns modelos (e.g., M7) apresentam uma qualidade de ajustamento deficiente. A análise dos resíduos dos modelos confirma esta conclusão. Os ganhos de longevidade observados não são homogéneos ao longo de todo o espectro de idades analisado, sendo mais significativos nas idades compreendidas entre os 60 e 80 anos, consequência dos avanços registados nas últimas décadas no tratamento das doenças cardiovasculares e do cancro. A maioria dos modelos revela uma boa qualidade de ajustamento, como se observa nos indicadores reportados na Tabela 2 para a população total. Considerando, por exemplo, a métrica SMAPE, o modelo APC apresenta o melhor desempenho preditivo na amostra de teste, seguido dos modelos HUw, CPspl e do modelo RSVD. Os resultados obtidos considerando outras métricas de avaliação não alteram grosso modo esta hierarquização da capacidade preditiva na população total portuguesa, registando-se desempenho similar nas subpopulações masculina e feminina.
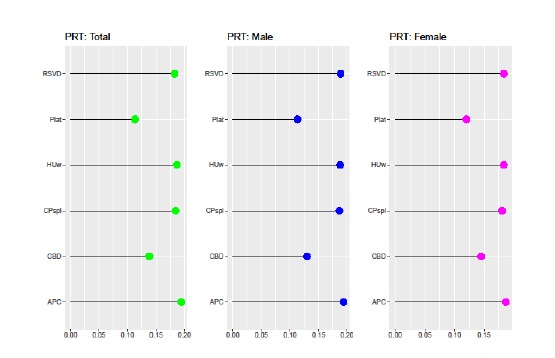
A Figura 2 ilustra a aplicação da metodologia BME adaptativa representando não apenas os modelos seleccionados para efectuar a BME, como os respectivos ponderadores, calculados através da função exponencial normalizada. A Figura explicita o contributo individual de cada modelo para a projecção da mortalidade e da esperança de vida e reflecte o diferente poder preditivo dos modelos seleccionados. A análise da Figura 2 permite verificar, na população total e subpopulações masculina e feminina, que os modelos LC, RH e M7 foram preteridos na combinação final em resultado da selecção prévia de modelos encaixados com melhor desempenho preditivo. A combinação Bayesiana de modelos seleccionada nas três subpopulações é idêntica, não significando tal que os ponderadores usados em cada subpopulação são os mesmos, dado que esta é função do diferente desempenho preditivo constatado em cada caso e este não é idêntico na amostra. Os modelos com maior contributo para a combinação final de modelos são os que apresentam os valores mais reduzidos na métrica SMAPE, ou seja, os modelos APC, HUw, CPspl e RSVD.
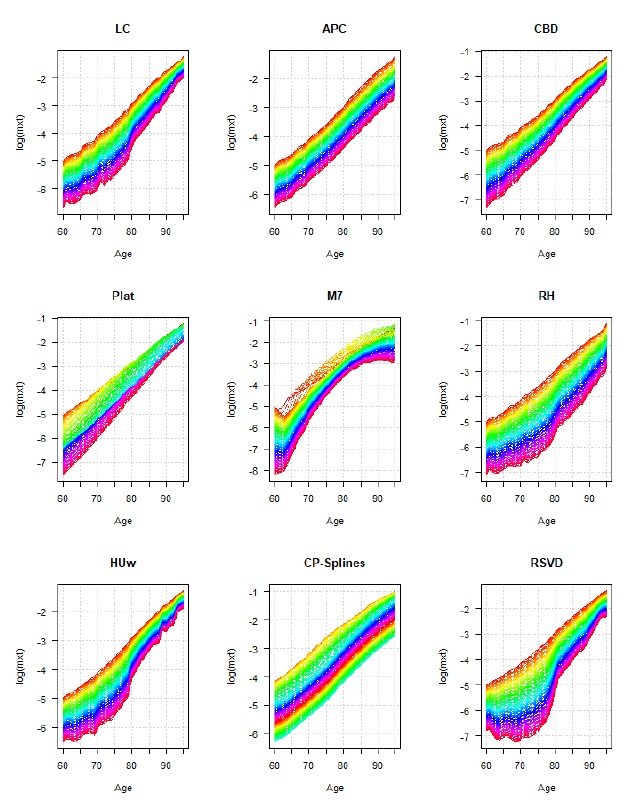
Figura 1 Quocientes de mortalidade ajustados, por modelo, População TotalNota: valores em escala logarítmica. Em cada gráfico, os valores mais baixos correspondem aos anos de observação mais recentes
Tabela 2 Métricas de avaliação dos modelos de projecção da mortalidade, População Total
| Modelo | |||||||||
| Métrica | LC | APC | CBD | Plat | M7 | RH | HUw | CPspl | RSVD |
| MAE | 0,00349 | 0,00334 | 0,00772 | 0,00806 | 0,00793 | 0,00713 | 0,00365 | 0,00435 | 0,00415 |
| MAPE | 0,04772 | 0,04212 | 0,07079 | 0,08709 | 0,17877 | 0,05498 | 0,04545 | 0,04747 | 0,04953 |
| MASE | 0,24415 | 0,24128 | 0,45738 | 0,49060 | 0,50616 | 0,37641 | 0,27165 | 0,33397 | 0,31772 |
| MDAE | 0,00159 | 0,00125 | 0,00197 | 0,00379 | 0,00572 | 0,00113 | 0,00139 | 0,00139 | 0,00101 |
| MSE | 0,00004 | 0,00004 | 0,00023 | 0,00022 | 0,00014 | 0,00036 | 0,00004 | 0,00007 | 0,00007 |
| RMSE | 0,00610 | 0,00656 | 0,01515 | 0,01481 | 0,01175 | 0,01887 | 0,00643 | 0,00843 | 0,00820 |
| RMSLE | 0,00510 | 0,00538 | 0,01209 | 0,01187 | 0,00982 | 0,01448 | 0,00538 | 0,00695 | 0,00680 |
| RMSPE | 0,05816 | 0,05207 | 0,08451 | 0,09895 | 0,25126 | 0,07409 | 0,05626 | 0,05962 | 0,06351 |
| RRSE | 0,07636 | 0,08419 | 0,16599 | 0,16294 | 0,13739 | 0,20283 | 0,08280 | 0,11200 | 0,10805 |
| RSE | 0,00583 | 0,00709 | 0,02755 | 0,02655 | 0,01888 | 0,04114 | 0,00686 | 0,01254 | 0,01168 |
| SMAPE | 0,04839 | 0,04236 | 0,07378 | 0,09192 | 0,17570 | 0,05725 | 0,04607 | 0,04727 | 0,04809 |
| SSE | 0,00669 | 0,00774 | 0,04129 | 0,03950 | 0,02486 | 0,06410 | 0,00744 | 0,01279 | 0,01212 |
Notas: MAE: mean average error; MAPE: mean average percentage error; MASE: mean absolute scaled error; MDAE: median absolute error; MSE: mean squared error; RMSE: root mean squared error; RMSLE: root mean squared log error; RMSPE: root mean square percentage error; RRSE: root relative squared error; RSE: relative squared error; SMAPE: symmetric mean absolute percentage error; SSE: error sum of squares.
3.2. Projecções de mortalidade e de esperança de vida
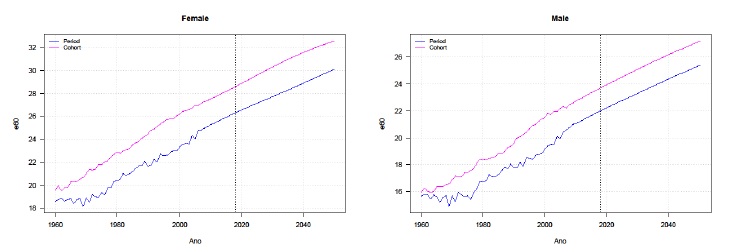
A Figura 3 apresenta a projecção da esperança de vida à idade 60 por período e por coorte no período 1960-2050, desagregada por sexo. Os resultados obtidos permitem concluir que o modelo de previsão antecipa, para ambos os sexos, a continuação da tendência de crescimento quase linear da esperança de vida registada nas últimas décadas. Em 1960, a esperança de vida por coorte na aproximação à idade de saída do mercado de trabalho era de cerca de 20 anos para as mulheres e de 16 anos para os homens. Neste estudo prevemos que em 2050 a esperança de vida das mulheres aos 60 anos suba para um valor superior a 32 anos (27 anos no caso dos homens), ou seja, antecipamos um aumento da longevidade e do gradiente entre homens e mulheres.
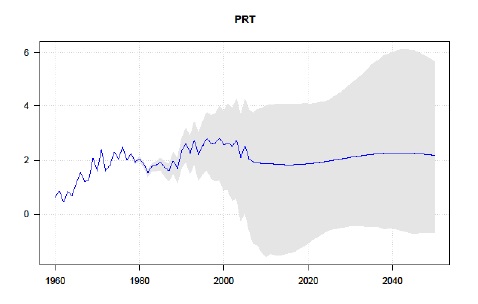
Este incremento contribui para o envelhecimento do topo da estrutura etária da população portuguesa, já de si hoje muito significativo, com implicações relevantes na dinâmica do mercado de trabalho, na sustentabilidade dos sistemas de protecção social financiados em repartição contemporânea e na capacidade e adequação dos sistemas públicos e privados de saúde e de apoio à dependência. O diferencial sistemático entre a esperança de vida por coorte e por período (life expectancy gap) é positivo para todas as subpopulações e anos analisados e não evidencia sinais de redução, o que significa que os indicadores por período actualmente usados nos organismos oficiais de estatística (e.g., pelo Instituto Nacional de Estatística) para estimar a longevidade remanescente da população e analisar os níveis de envelhecimento subestimam sistematicamente a «verdadeira» esperança de vida da população, introduzem impostos/subsídios implícitos entre gerações no sistema de protecção social, e distorcem as decisões de participação no mercado de trabalho, de consumo ou de poupança, com implicações nos pension entitlements (Bravo e Herce, 2020). A Figura 4 representa a previsão pontual e o intervalo de confiança do gap de esperança de vida à idade 60 no conjunto da população portuguesa no período entre 1960 e 2050. Os resultados obtidos confirmam o crescimento do gap no período analisado e uma estabilização em torno dos 2 anos, com um limite superior do intervalo de confiança que pode chegar aos 6 anos em 2050.
O gap é um indicador da injustiça actuarial intergeracional do sistema de pensões na medida em que sinaliza o número de anos de pagamento de prestações sociais que as gerações de actuais beneficiários usufruirão em excesso face às contribuições sociais que efectuaram durante a vida activa (em conjunto com as das respectivas entidades empregadoras). A este imposto implícito de cerca de 10% da riqueza em pensões (pension wealth) pago pelas actuais gerações de trabalhadores no activo acrescem outros que resultam dos diferenciais de longevidade entre grupos socioeconómicos e entre sexos, por exemplo. A sua redução/eliminação requer a adopção de reformas nos sistemas de protecção social (e.g., aumento da idade normal de reforma, alteração do mecanismo de indexação das pensões em pagamento, reformulação do factor de sustentabilidade) e a utilização de métricas adequadas da longevidade da população.
4.Conclusões
As previsões de longevidade da população são comummente realizadas com base num único método estocástico, assumindo que este representa da melhor forma a incerteza. Os resultados da aplicação de um modelo de previsão da mortalidade assente numa combinação Bayesiana de modelos heterogéneos evidenciam que esta escolha comporta significativos riscos de modelo e que a incerteza associada a previsões de longo prazo da longevidade da população é melhor representada por combinações de modelos com diferentes características. As projecções de esperança de vida por período e por coorte nas idades adultas apontam para a manutenção da tendência de crescimento da esperança de vida, para a existência de um gap significativo entre os indicadores por período e por coorte (e por sexo). Estes resultados, em conjunto com a existência de gradientes significativos na longevidade por grupo socioeconómico, confirmam a existência nos sistemas de protecção social de impostos/subsídios implícitos entre gerações que distorcem as decisões de consumo, de mercado de trabalho e de poupança e questionam a justiça intergeracional. A sua redução exige uma avaliação mais rigorosa da longevidade da população por parte dos decisores públicos e privados e a utilização de métodos de projecção mais robustos que incorporem todas as fontes de incerteza.