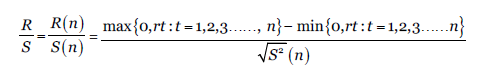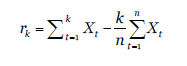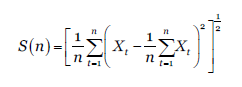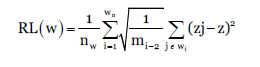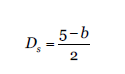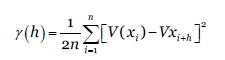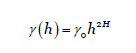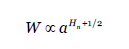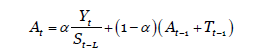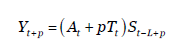1. Introducción
El turismo constituye una fuente de riqueza y desarrollo, pese a su vulnerabilidad por situaciones de conflictos sociales o emergencias sanitarias como el covid-19. La recuperación que muestra este sector, denota su resiliencia (Mendoza et al., 2021) y capacidad de adaptación, lo que en el mercado global se evidencia con el margen de estimación de ingresos que alcanzó 1.9 billones de dólares en el año 2021 a nivel global (NWTO, 2021). Sin embargo, la industria de la hospitalidad a nivel local puede presentar adversidades para incrementar la ocupación de cuartos. La ciudad de México por ejemplo reportó un margen de ocupación del 62% en periodo pre-pandémico (DATATUR, 2019), mientras que en tiempos de pandemia este dato oscilaba alrededor del 30% en el año 2021 (Camila, 2022). Por tanto, el éxito de la administración de estas empresas depende en gran medida de los medios analíticos para mejorar la previsión de datos, es decir trabajar sobre la precisión de las predicciones (Liu et al., 2014), lo que demanda un esfuerzo para desarrollo nuevos procedimientos matemáticos con la intención de identificar parámetros que se adapten a las necesidades del presente y con ello propicia el crecimiento y buen funcionamiento de las empresas al tiempo que se utilizan tecnología y sistemas de información que mejoren la toma de decisiones en la industria (Patiño et al., 2020).
La venta de servicios de hospedaje se realiza a través de la configuración tarifaria, lo que significa que los clientes reciben ciertos productos y servicios de acuerdo a los tipos de segmento a los que pertenecen (Liu et al., 2022), ejemplo de ello lo constituyen las condiciones particulares que integran el servicio (Somphong et al., 2022) como la ubicación del cuarto, el acondicionamiento, las amenidades y otros bienes de consumo. No obstante, el comportamiento de las tarifas hoteleras ha sido poco estudiado.
El análisis de datos en hotelería supone incluir aquello aspectos que hacen variar las cifras de manera dinámica para determinar patrones a partir de la complejidad de los fenómenos. Los fractales denotan el comportamiento por puntos de cambio, que a su vez se pueden explican por leyes de potencia. La teoría de la complejidad ha sido de gran utilidad para explicar situaciones en distintas ramas del conocimiento como la economía (Kachhia, 2023), la física (Hou et al., 2021), la mecánica (Peng, & Li, 2023), las ciencias sociales (Blanco, 2019) y en el turismo (Briones et al., 2011) por su gran capacidad para detectar patrones en series temporales.
Debido a que se examinará una serie que aparentemente es aleatoria se busca la repetición por escalas y a distintos niveles. Así, la compatibilidad estadística en fractales auto-afines, se presenta por un conjunto que muestra ser invariante por escalamiento. En este trabajo se propone desarrollar un análisis de tendencias futuras de series complejas en tarifas para determinar la estimación optimizada de parámetros. Para ello, se desarrollan las siguientes fases: 1) se recaban los datos con el sistema de ingresos de un hotel de la Ciudad de México. 2) Se realizan particiones de los valores por desviaciones estándar y se da a conocer el comportamiento de la seria a distintas ventanas de orden “n”. 3) Se estiman los exponentes de Hurst y se presentan las ilustraciones log-log por método, para indicar el más apropiado que genera punto de estacionalidad y antipersistencia. 4) Se prueba la longitud del ciclo obtenida en el modelo Holt-Winters y se obtienen los parámetros optimizados. 5) Se presentan la gráfica de ajuste con los valores utilizados, y la predicción de los primeros 8 datos de la serie. 6) Se vierten las conclusiones y recomendaciones finales.
2. Revisión de la bibliografía
El análisis de datos se encuentra ligado al uso tecnológico en empresas de hotelería no solamente para apoyar en las decisiones, sino para optimizar y maximizar los beneficios (Pimentel et al., 2019) ya que la información generada desde la gestión constituye una serie de datos que se gesta desde una estructura compleja (Hernández et al., 2021).
Algunos de los temas centrales en el manejo de cifras en la industria de la hospitalidad son los aspectos financieros (Ozdemir et al., 2021), la calidad de servicios (Nilashi et al., 2021) y el uso de los recursos (Iranmanesh et al., 2022). Sin embargo el análisis de datos toma relevancia significativa para revelar tendencias de comportamiento y con ello mejor la generación de fuentes de información confiables que direccionan la planeación de acciones en el servicio (Pan et al., 2012). Derivado de la gran necesidad de la industria turística se han empleado distintas herramientas para comprender, explicar y predecir la tendencia de datos en estas empresas, como se muestra en la tabla 1, que sintetiza algunos de los esfuerzos para adecuar modelos de previsión con base en datos recolectados.
Tabla 1 Métodos de previsión de datos en empresas turísticas
| Técnica | Explicación | Autores |
|---|---|---|
| Modelos de de explicación automático | Combinación de modelos dinámicos de pronostico | (Pereira & Cerqueira, 2022) |
| Modelo de memoria de atención a corto y largo plazo | Usa datos de la demanda con características adicionales proporcionadas por una empresa de turismo. | (Kaya et al., 2022) |
| Modelo de aprendizaje profundo. | Usa correlaciones espaciales y temporales por medio de algoritmo bayesiano | (Huang & Zheng, 2021) |
| Modelo de previsión de cancelaciones en hotelería | Usa técnicas de redes neuronales optimizadas con algoritmos genéticos | (Sánchez-Medina & C-Sánchez, 2020) |
| Modelo de precios de las habitaciones | Usa modelo de promedio móvil, la máquina de Boltzman, el modelo de máquina de vector y el sistema de interferencia difusa de red adaptativa. | (Al Shehhi & Karathanasopoulos, 2020) |
| Modelo de pronóstico de series temporales | Usa el espacio de estado estacional | (Pereira, 2016) |
| Modelo de serie temporal con fuente de datos big data | Usa múltiples fuentes de big data | (Pan & Yang, 2017) |
| Modelo de redes neuronales | Redes con revisión de puntaje | (Chang et al., 2021) |
Pese, a que se ha incrementado el número y tipo de técnicas numéricas en la hospitalidad, existe muy poca evidencia sobre el análisis de tarifas hoteleras. En este sentido Kim et al., (2020) desarrollaron un estudio de tarifas y la discrepancia entre los canales de distribución con la intención de conocer los criterios sobre los cuales se calculan los precios. Por su parte Lee (2011), aborda el cambio en las tarifas y subraya que el número de turistas y el desempeño económico se relacionan de forma positiva con su incremento. De igual manera Lim & Ok (2022), determinaron como las tarifas promocionales influían en las percepciones de los clientes. En contraste, la previsión de tarifas muestra poco interés por parte de los académicos y los analistas del turismo y la hotelería. Con el propósito de abonar a las herramientas de analíticas y dado que la pandemia de convid-19 ha incentivado el uso de la teoría compleja para realizar mediciones en la dinámica temporal de series de datos (Castillo & Melin, 2020) y debido a que su uso ha sido recurrente dado a que también describe la trayectoria de la enfermedad (Easwaramoorthy et al., 2021). En este trabajo se abordan los datos bajo la teoría de la complejidad, la cual ha sido utilizada en turismo para dar explicar la dinámica de datos a partir del dinamismo del sector (Baggio & Sainaghi, 2011;Baggio & Sainaghi, 2016;Baggio, 2014).
La intención de refinar los modelos de pronóstico en la industria recae en el hecho de constituir herramientas que apoyen en la toma de decisiones gerenciales en la industria (Teixeira & Gunter, 2023). En tal sentido, han sido de gran utilidad las técnicas Box-Jenkins en su forma SARIMA y ARMA (Chuwang & Chen, 2022); los modelos de series de tendencias estructurales para identificar variables y dentar una mejora en la previsión de datos (Rashad, 2022); la combinación de técnicas de inteligencia artificial y enfoques convencionales que dan pie a modelos híbridos (Ouassou & Taya, 2022) y el uso de arquitecturas de redes neuronales con caracterización de periodos (Nguyen et al., 2022).
Estos esfuerzos tienen la intención de constituir métodos técnicas y herramientas que inducen modelos aplicables a la industria. (Gunter, 2021) especialmente en tiempos de pandemia en los que se vio afectado el flujo de turistas y de manera directa las comunidades residentes en los que se enclavan los atractivos turísticos (Godovykh et al., 2021).
3. Metodología
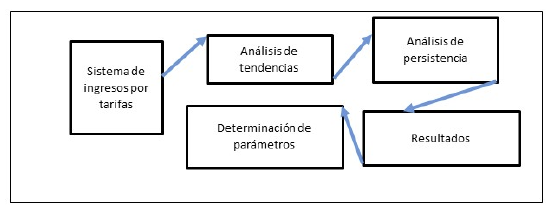
A continuación se presenta la metodología que sigue este trabajo en la figura 1, en la cual se puede percibir las fases que sigue la investigación. Cabe señalar que el cálculo de los parámetros ayudó en el desarrollo de datos futuros a partir del reconocimiento de las tendencias en los datos. Bajo esta consideración, enseguida se hace la descripción de los apartados para comprender el proceso que se siguió en este artículo.
3.1. Sistema de ingresos por tarifa.
En esta fase primero se compilaron los datos a partir del sistema central de información del hotel (PMS) Property management system por sus siglas en idioma inglés, en un hotel categoría cinco estrellas. En esta empresa se asigna una clave a cada tipo de tarifa para poder otorgarla a los clientes. El gerente de recepción gestiona el otorgamiento de las tarifas según corresponda y tiene la facultad junto con la gerencia en turno de integrar servicios adicionales como llamadas telefónicas, alimentos, amenidades y promociones. Estos aspectos en general representan relaciones numéricas que cambian el total de ingresos por cada tarifa y la suma total de los datos que se observan.
El sistema central de información permite obtener datos por códigos y conceptos desglosados. El concentrado de la participación, su definición y el tipo de tarifa aparece en la tabla 2, que además muestra el porcentaje de participación de cada tipo de tarifa. Partiendo de la base anterior, se toma los datos de entrada del modelo, mismos que se constituyen con la sumatoria de las tarifas registradas en cada una de las observaciones que contabilizaron 974 de ellas.
Tabla 2 Tipología de tarifas del hotel.
| Tipo de tarifa | Concepto | Porcentaje de representación |
|---|---|---|
| Corporaciones | Tarifa de descuento por ocupaciones | 7% |
| Regular | Se brinda en recepción para clientes sin reservaciones | 12% |
| Contratos | Se ofrece a partir de garantizar cierto número de estancias al año | 19% |
| Gobierno | Tarifa preferencial a miembros diplomáticos y otros gobernantes | 12% |
| Promocional | Se determina por la temporalidad | 5% |
| Paquete | Incluye elementos de paquete | 4% |
| Descuento | Se ofrece en temporada baja y fines de semana | 6% |
3.2. Análisis de tendencias
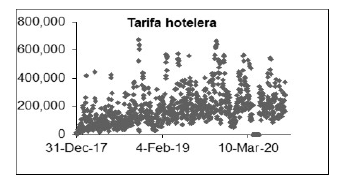
Con el conjunto de datos se procedió a desarrollar el gráfico 2, para observar la dinámica a través del tiempo de los datos históricos de la serie y analizar su comportamiento. A primera vista, la serie parece aleatoria. Sin embargo bajo un análisis cualitativo se observan los siguientes aspectos:
Se observan oscilaciones periódicas, sin embargo es difícil precisar el número cíclico que describa la tendencia y la estacionalidad de la serie.
Se muestra que en el mes de abril del año 2022, no contabilizan ingresos por tarifas ya que el establecimiento permaneció cerrado en estas fechas debido a la contingencia sanitaria por covid-19.
Los datos mantienen una tendencia ascendente.
Para detectar la existencia de patrones repetidos se realiza una fragmentación de la serie en ventanas a partir de las desviaciones estándar de los datos; es decir, para la ventana 1, se calculó (sigma) del dato 1 al dato 2 ( σ 1 , σ 2 ), y así de manera sucesiva hasta completar 100 datos ( 𝜎 𝑛 , 𝜎 𝑛+1 ). Lo mismo se realizó con las ventanas sucesivas ampliando este cálculo a partir del dato 110 hasta 500, con conjuntos de 10 datos ( ?? 101 , 𝜎 111 ).y de 500 a 1000 con conjuntos de 50 datos. La tabla 3, muestra el procedimiento y las ventanas que se toman como muestra para analizar las tendencias.
Tabla 3 Ventanas de muestra de la serie tarifas hoteleras.
| Fecha | Datos | Ingresos por Tarifas | |||
|---|---|---|---|---|---|
| 01/01/2018 | 1 | 13,377.99 | n=10 | ||
| 02/01/2018 | 2 | 5,851.44 | 17.0315625 | n=20 | |
| 03/01/2018 | 3 | 3,003.84 | 61.036875 | 0.375507812 | n=30 |
| 04/01/2018 | 4 | 3,588.48 | 207.6428125 | 0.033203125 | 7.69043E-05 |
| 05/01/2018 | 5 | 3,669.12 | 197.1746875 | 0.255791016 | 0.000500488 |
Se tomó una muestra de 3 observaciones con la misma distancia de 𝑛, para visualizar si existe similitud, el origen de la muestra depende de las ventanas analizadas y de la comprobación de las tendencias del comportamiento gráfico en los datos. Para este caso se comprueba similitud en las fluctuaciones de las ventanas seleccionadas al observar las figuras 3, 4 y 5 respectivamente.
En la comparación de la las figuras 2 y 3, se preservan los picos de ascenso en los datos máximos.
Con las figuras 3, se puede apreciar que a diferentes valores de ventana n, se guarda una similitud palpable en las tendencias de la serie. Esta partición de datos responde a la necesidad de visualizar el cambio relativo en cada iteración para valorar la pertinencia de desarrollar un análisis que induzca la identificación de parámetros a partir de patrones similares a distintas recursiones.
3.3. Análisis de persistencia.
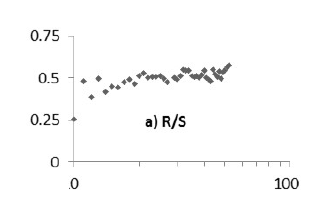
Con la certeza de que se puede encontrar una base de comportamiento que describa la serie, se realiza un análisis de persistencia de los datos a través del exponente de Hurts o exponente H. Lo anterior, para determinar si existe estacionalidad. Para ello, se utiliza el softare Benoit 1.31, dado que la serie muestra aleatoriedad a primera vista, se desarrollan las gráficas log-log del exponente con distintos métodos de tratamiento auto-afín. Primero se empleó el método R/S o rango reescalado, el cual arroja un valor H, que mide la intensidad de dependencia a largo plazo de las series temporales.
Donde: 𝑋= 𝑋,:𝑡=1,2,3…… 𝑛 , y 𝑅(𝑛) es normalizada por la desviación estándar 𝑆(𝑛). Así, el rango rescaldado se define por 𝑛 𝐻 , donde 𝑛→∞, en una serie con traza auto-afín.
En la figura 4, se observa una estacionalidad cercana al 0.5 por lo tanto, bajo este método la serie sigue siendo aleatoria y no se observan persistencias que favorezcan la previsión de datos, esto debido a que los exponentes H, vierte estacionalidad alrededor del punto medio =0.5.
En segundo lugar se utilizó la longitud de rugorosidad o método R/L que se mide como el valor de la raíz cuadrada media del residuo en una tendencia lineal ajustada a los puntos de muestra en una ventana de longitud 𝑤, entonces la rugosidad de la raíz cuadrada media se calcula como sigue:
Donde 𝑛 𝑤 es el número total de ventanas de longitud 𝑤, ?? 𝑖 es el número de puntos en la ventana, 𝑤 𝑖 , 𝑧 𝑗 es el residual en la tendencia y 𝑧 es la media residual en la ventana 𝑤 𝑖 .
En la figura 5, se observa que con el método R/L se estacionaliza la serie en el dato 8, esto se presenta con valores de H alrededor de 0.70, lo que significa que existe persistencia traducida en la visualización del exponente H por encima del promedio, este gráfico ilustra un posible parámetro para precisar el comportamiento de la serie.
De la misma forma el análisis incluyo el Método de espectro de potencia P/S, el cual se relaciona con el exponente H a través de “b” como la pendiente negativa cuya forma matemática se constituye por:
Con este análisis se observa en la figura 6, que a partir del dato 22 la fórmula arroja datos cero para continuar con tendencia alcista. Por tanto, los valores del exponente H, no presentan estacionalidad alguna.
El siguiente método a valorar fue el variograma o V/R definido como el cuadrado medio del incremento de puntos, estimado de la siguiente manera:
Donde ℎ, es la distancia de seguimiento (distancia entre dos puntos sucesivos), 𝛾 (ℎ) es el variograma a distancia de seguimiento ℎ (el número de pares a una distancia h de retraso) y 𝑉( 𝑥 𝑖 ) son los valores de la muestra en la ubicación 𝑥 𝑖 , entonces las distribuciones del fractal se caracterizan por un modelo de variograma de la siguiente forma:
Donde 𝐻, es el exponente de Hurst. Los métodos de rugosidad-longitud y variograma se basan en el comportamiento de la escala de la desviación estándar 𝑆 𝑛 ∝ 𝜏 𝐻 𝑛 y la semi-varianza 𝑉𝑎𝑟∝ 𝜏 2𝐻 .
Este método muestra en la figura 7, datos oscilando alrededor H= 0.25 y con datos ceros después de la observación 27, lo que denota incapacidad para identificar previsiones.
Finalmente se valoró el método de veletas el cual se asocia con un coeficiente:
Donde 𝑎 es el un parámetro que mide la onda.
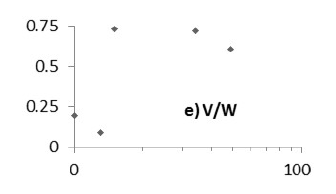
En este último análisis en la figura 8, solo aparecen los datos por debajo de 0.75, sin mostrar estabilidad ni punto de saturación.
3.4. Resultados
Con las fases desarrolladas hasta ahora se presentan a continuación los resultados observados.
La manera en la que están constituidas las tarifas hoteleras y la flexibilidad que tiene la gerencia para modificarlas además de la injerencia de fenómenos externos como el impacto del covid-19 generan comportamiento caótico en la serie difícil de caracterizar.
La serie muestra auto-afinidad de tendencias al ser observada mediante el análisis de desviaciones estándar.
La serie de datos de las tarifas hoteleras, solo se estaciona en el dato 𝐻=8 en el método de longitud de rugorosidad o L/R, en que además se muestra persistencia entre los datos, por tanto se tiene posibilidad de estimar parámetros que expliquen el comportamiento de los datos.
Dado que el dato de saturación se puede interpretar como un ciclo de longitud de la serie se realiza una prueba para estimar parámetros en el del modelo aditivo de Holt-Winters. Lo anterior, debido a que la estacionalidad es constante, lo cual se realiza en el siguiente apartado.
3.5. Determinación de parámetros optimizados.
Los parámetros principales del método de Holt-Winters están constituidos de la siguiente forma:
α= Constante que actúa como atenuante para el promedio de datos (0< 𝛼<1)
β= Constante que actúa como atenuante de las tendencias estimadas 0< 𝛼<1
𝛾= Constante de atenuación que actúa en la estacionalidad (0< 𝛾<1)
Para calcular el valor atenuado 𝐴 𝑡 , se usa la siguiente relación:
Donde
L= 𝐿𝑜𝑛𝑔𝑖𝑡𝑢𝑑 𝑑𝑒 𝑒𝑠𝑡𝑎𝑐𝑖𝑜𝑛𝑎𝑙𝑖𝑑𝑎𝑑
Para calcular la tendencia 𝑇 𝑡 , se utiliza la siguiente relación:
Para calcular el valor pronosticado 𝑌 𝑡+𝑝 se utiliza la siguiente fórmula:
Donde p= Periodos a pronosticar
Con la primer parte del análisis se toma L= 8 asumiendo con ello que cada 8 datos se repite el ciclo de comportamiento de los datos, con tendencia creciente excepto en el periodo de cierre por covid-19 de acuerdo con la figura 2. Para medir la adaptabilidad de los datos se desarrollan los siguientes procesos:
Se utilizan parámetros iniciales para el modelo.
Se realiza una optimización con la herramienta de solver de EXCELL.
Se realiza una optimización con el software winQSB.
Se vierten las conclusiones.
En la tabla 4, se muestran los parámetros iniciales y los optimizados por técnica analítica.
Tabla 4 Parámetros del modelo
| Parámetros | Iniciales | Optimizados | |
|---|---|---|---|
| L | 8 | Solver | WINQSB |
| Alfa (α) | 0.1 | 0.43433065 | 0.36 |
| Beta (β) | 0.2 | 0.83944777 | 0.78 |
| Gamma (γ) | 0.7 | 0.25185388 | 0.67 |
A partir de la información de la tabla 2, se prueban los parámetros iniciales obtenidos con la herramienta solver de Excell y los obtenidos con el software winQSB. Estos últimos remarcados en negritas en la tabla ya que minimizan el error del modelo de acuerdo con los siguientes coeficientes obtenidos.
De la misma manera, se vierten los coeficientes de errores mínimos en la tabla 5, la cual muestra: la desviación absoluta media (MAD) “Meand absolute desviation”, el error medio cuadrático (MSE) “mean squared error” y la media absoluta por error (MAPE).
Tabla 5 Coeficientes de error mínimo del modelo
| Coeficientes de error | Dato |
|---|---|
| MAD | 7866.99 |
| MSE | 8.43 |
| MAPE | 42.52 |
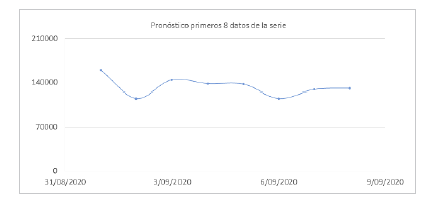
En el mismo sentido se procedió a calcular la predicción de los primeros 8 datos de la serie cuyos resultados se ilustran en la tabla 6 y en la gráfica 9.
Tabla 6 Primera predicción de la serie
| Primera serie pronosticada | Dato | ||
| S(1) | 159642.575 | S(5) | 137442.295 |
| S(2) | 115612.975 | S(6) | 115525.905 |
| S(3) | 144109.575 | S(7) | 129278.515 |
| S(4) | 138241.935 | S(8) | 130956.785 |
Finalmente se presenta el comparativo del ajuste de los parámetros encontrados en la figura 9, comparados con los datos históricos de la serie. En ella se observa que el uso de los parámetros mantiene un ajuste considerable con la serie original, lo cual muestra las bondades del modelo para predecir datos en el futuro. Cabe señalar que el pronóstico se puede calcular por bloques de 8 datos como aparece en la figura 10 para obtener datos futuros que contengan la relación interna de la serie original.

Figura 9 Ajuste del comportamiento de la base de datos tarifas hoteleras, actual y modelo aditivo de Holt-Winters.
4. Conclusiones
La previsión de datos en turismo y hotelería es una de los aspectos importantes dado que la emergencia de covid-19 ha generado impactos directos en la forma de estimar valores que apoyen los cursos de acción tomados por la dirección de las empresas. El turismo en este sentido se comporta de manera compleja dado que los datos analizados pueden contener información sin registro de ventas por tarifas hoteleras, tal es el caso del mes de abril del 2020 de la serie analizada.
Para poder realizar un modelo de previsión de datos en este trabajo se propuso la revisión de las tendencias de la serie para visualizar comportamientos afines a distintos valores de n, el uso de cinco métodos de análisis de persistencia a través del coeficiente H o de Hurts para conocer la estacionalidad y el punto de cambio de sentido en las grafías en escalas logarítmicas. El resultado utilizado en el modelo aditivo de Holt-Winters parte del gráfico de longitud de rumorosidad 𝑳/𝑹 con una estacionalidad en el tiempo n=8, este dato se usa como ciclo de longitud del modelo aditivo de Holt-Winters cuyos parámetros (a=0.36, b=0.78, y=0.67), minimizan el error presentado. Con este artículo se concluye que la combinación de herramientas matemáticas resulta pertinente para estimar el comportamiento de la serie de las tarifas hoteleras y describir la dinámica interna de los datos.
Estos resultados se pueden utilizar para mejorar la toma de decisiones en la gestión de servicios, a través de la ampliación del modelo para idéntica escenarios futuros del comportamiento de las tarifas que a su vez representen el comportamiento de la demanda para programar recursos físicos humanos y materiales en la gestión de servicios. Sin embargo este trabajo se limita solamente a encontrar la relación de parámetros que minimizan el error en la serie. Para futuras investigaciones se recomienda trabajar con los rendimientos logarítmicos de la serie y probar métodos que sean compatible con los resultados encontrados.