ARTIGO

 

Medidas e escalas de desigualdade de renda em perspectiva

Measures and scales of income inequality in perspective

 

Libório, Mateus¹; Martinuci, Oseias²; Bernardes, Patrícia¹; Ekel, Petr³

¹Pontifícia Universidade Católica de Minas Gerais, Programa de Pós-graduação em Administração; Av. Itaú, 525 - Bairro Dom Cabral, 30535-012, Belo Horizonte, Brasil; m4th32s@gmail.com; patriciabernardes@pucminas.br  

²Universidade Estadual de Maringá, Centro de Ciências Humanas Letras e Artes, Departamento de Geografia; 87020-900, Maringá, Brasil; osmartinuci@uem.br

³Pontifícia Universidade Católica de Minas Gerais, Programa de Pós-graduação em Engenharia Elétrica; 30535-012, Belo Horizonte, Brasil; pekel@superig.com.br  

 

RESUMO

Estudos mostram que existem diferentes abordagens para se medir a desigualdade de renda. Contudo, faltam análises empíricas que apliquem as diferentes formulações a uma mesma unidade de análise, demonstrando as implicações da alteração da escala de análise nos seus resultados. A partir dessa constatação, neste artigo, são apresentadas diferentes medidas de desigualdade de renda aplicadas em diferentes escalas (cidade e setores censitários urbanos). Os resultados sugerem que os setores censitários, ao concentrarem famílias de renda semelhante, tendem a ser menos desiguais internamente e mais desiguais na inter-relação com outros setores. Concluí-se que a medida de desigualdade de renda é sensível à escala de análise. Distorções significativas no índice de desigualdade de renda provocadas pela alteração da escala desfavorecem as comparações do índice entre diferentesescalas, mas, ao mesmo tempo, favorecem a inferência do grau da desigualdade de renda intraurbana

 

Palavras-chave: desigualdade de renda, setores censitários, análise multivariada de dados.

 

ABSTRACT

Studies show that there are different approaches to measuring income inequality. However, there is a lack of empirical analyses realized for different approaches, applied to the same unit of analysis, demonstrating the implications of changing the scale of analysis in its results. From this statement, in this paper, we present different measures of income inequality applied at different scales (city and urban census tracts). The results show that the census tracts with concentrating families of similar income, tend to be less unequal internally and more unequal in the interrelationship with other sectors. It is concluded that the measure of income inequality is sensitive to the scale of analysis. Significant distortions in the income inequality index caused by the change in the scale disfavor the comparisons of the index between different scales, but, at the same time, favor the inference of the degree of intra-urban income inequality.

 

Keywords: income inequality, census tracts, multivariate data analysis.

 

 

1. Introdução

A desigualdade nas sociedades modernas tem sido um problema recorrentemente debatido. A crise eclodida no mercado americano no ano de 2008 deu um novo impulso à questão. No período recente tornaram-se famosas as obras, por exemplo, de Joseph Stieglitz, prêmio Nobel de economia, e de Thomaz Piketty. O primeiro com a obra “O preço da desigualdade” e o segundo com “Economia da desigualdade”. Os argumentos de ambos os autores convergem para o entendimento de que a desigualdade social faz mal tanto para a economia quanto para toda a sociedade e, em última instância para a própria democracia (Stieglitz, 2016). Esse tema, que costuma opor direita e esquerda, liberais e socialistas, não levanta divergências quanto ao seu caráter de injustiça. A divergência está, isso sim, na forma de superá-la (Bobbio, 2011; Piketty, 2015).

Na literatura internacional que trata do tema, o Brasil é frequentemente elencado como um exemplo de um país rico que ostenta altos níveis de desigualdade econômica. Apesar dos inúmeros avanços acontecidos desde a promulgação da Constituição de 1988, o Brasil continua, ainda, entre os mais desiguais do mundo (Arrecthe, 2015, p. 2). Se por um lado, entre 1988 e 2015, reduziu-se de 35% para menos de 10% a população brasileira abaixo da linha da pobreza, e 16% nos níveis de desigualdade (OXFAM, 2017), por outro lado, de acordo com uma recente publicação da PNUD (2017), o Brasil ocupa a 10ª posição no ranking de desigualdade no mundo. Vê-se que no caso brasileiro, a desigualdade de renda, medida pelas referidas instituições, ocupam um lugar de destaque no debate acerca do fenômeno da desigualdade social. Vários estudos evidenciam a caráter complexo e multifacetado da desigualdade social no Brasil, como aqueles reunidos nos livros “Trajetórias das desigualdades”, organizado por Marta Arretche (2015), “Exclusão social em cidades brasileiras”, organizado por Everaldo Santos Melazzo e Raul Borges Guimarães (2010), “Medidas de cidades” de Dirce Koga (2003) e “Mapa da exclusão social na cidade de São Paulo” de Aldaíza Sposati (1996). Em todas essas obras, a renda é sempre um indicador importante na composição de um quadro mais amplo e complexo do problema da desigualdade social. Diante de inúmeras possibilidades de análise, este trabalho, entretanto, centra a sua preocupação na avaliação de medidas de desigualdade de renda aplicadas a diferentes escalas.

A produção acadêmica sobre o problema da desigualdade de renda, por sua vez, é significativa, tanto na escala nacional (Amarante e Colacce, 2018) e estadual (Hoffmann, 2017), quanto na escala intraurbana (Villaça, 2001; Lindo, 2011; Silveira e Muniz, 2014).

Na escala intraurbana, Melazzo e Guimarães (2010) e Melazzo, Ferreira e Miyazaki (2003) mostram que a análise das desigualdades a partir renda não é suficiente para compreender a desigualdade social como um todo. Ao mesmo tempo, estes autores mostram que a desigualdade de renda é capaz de evidenciar o processo de diferenciação das áreas urbanas, sobretudo o processo de homogeneização da renda na escala interna (dentro das áreas) e da diferenciação externa (entre áreas).

Independentemente da escala, estes estudos permitem medir e analisar a desigualdade de renda entre países, estados e áreas intraurbanas ou sua dinâmica temporal, porém, se preocupam pouco em medir e analisar a desigualdade de renda entre diferentes escalas, e, logo, em responder: i) em que medida o efeito do processo de homogeneização da renda na escala intraurbana influencia a medida de desigualdade de renda?; ii) quais as implicações desse efeito nas comparações de desigualdade de renda em diferentes escalas?

Responder tais questões seria, conforme Castro (2017) um ponto relevante, pois tão importante quanto saber que o fenomeno se altera com a escala, é saber como tais fenomenos mudam e quais são os novos conteúdos nas novas dimensões (que neste caso seria medir o efeito da homegenização interna nas medidas de desigualdade de renda).

Corroborando com a ideia de que a escala geográfica tem implicações nas características e na dinâmica dos fenômenos (Melazzo e Castro, 2015), objetivamos, com este texto, apresentar evidências empíricas de que a medição e a análise da desigualdade de renda devem considerar os efeitos que a escala produz neste índice, aprofundando-nos na medida de desigualdade de renda intraurbana (no nível dos setores censitários).

Na medida em que a renda é um indicador importante do desenho de sistemas de indicadores sociais (Jannuzzi, 2012) e que recebem atenção especial em processos de mapeamento e em análises espaciais da desigualdade social intraurbana (Koga, 2003; Melazzo e Guimaraes, 2010), faz-se necessário aprofundar o entendimento de suas características e de suas alterações conforme sua topologia e conforme a escala. Este texto, portanto, procura contribuir para as discussões sobre a dimensão da renda, comumente presente em sistemas de indicadores, sobretudo daqueles relacionados à desigualdade social. Nesse sentido, considerada a complexidade do tema desigualdade social e dado que estamos tratando apenas de uma parte dele, este texto não tem como objetivo esgotar tal discussão, e sim, ao acrescentar a perspectiva da escala, ampliar as discussões às quais importem a desigualdade de renda, mais detalhadamente na escala intraurbana.

Para tanto, analisamos e aplicamos modelos para a medição e análise da desigualdade de renda, expostos a seguir, tomando como exemplo, uma cidade de porte médio, a terceira maior do Estado do Paraná, no Brasil, com população estimada, em 2018, de mais de 400 mil habitantes, e que exerce importantes funções no âmbito da rede urbana paranaense, podendo, portanto, também ser qualificada como cidade média.

 

 

2. Medidas de desigualdade de renda

Jenkins (1991) observa que a avaliação dos resultados de políticas públicas que procuram maximizar o bem-estar social é, geralmente, baseada nas informações sobre a distribuição de renda (índices de desigualdade). Amartya Sen (1993) acrescenta que a análise da desigualdade de renda deve ser baseada em variáveis objetivas, sendo a distribuição de renda e a riqueza as mais comuns, e que outras variáveis como, por exemplo, padrão de vida podem enriquecer as análises.

Melazzo, Ferreira, Miyazaki (2003) alertam que a distribuição de renda (símbolo do capital econômico) pode ser uma medida ampla e adequada para medir a desigualdade de renda, mas não é mais do que uma entre as muitas variáveis que compõe a análise multidimensional da desigualdade social. Por exemplo, Jenkins (1991) sugere enriquecer a análise da desigualdade social incluindo a despesa (consumo doméstico), ao considerá-la uma variável que representa o exercício efetivo da disponibilidade de renda.

Para se análisar a desigualdade social em suas multiplas dimensões é preciso organizar, sumarizar descrever e relacionar variáveis, e por meio da estatística descritiva, medir índices e verificar relações entre variáveis (Oliveira, Dalmônica e Silva, 2011). Contudo, a presença de diferentes tipos de variáveis e técnicas de tratamento de dados pode tornar a construção e escolha dos índices de desigualdade social uma tarefa difícil. Além disso, alterações na escala geográfica, ao condicionar a maneira de apreender e lidar com o objeto da análise, podem mudar dinamicamente os índices de desigualdade social, pois alteram as próprias condições de produção e circulação (Melazzo e Castro, 2015).

Vimos que muitas pesquisa se dedicaram em superar as muitas dificuldades técnicas e metodológicas para tratar os múltiplos dados e variáveis que devem compor os índices de desigualdade social. Apesar da importância destas pesquisas para a compreensão da desigualdade social, o efeito das mudanças na alteração da escala nos índices de desigualdade social permanece pouco compreendido.

Tomando a desigualdade de renda intraurbana como um exemplo, a homogeneização a distribuição da renda na escala interna (dentro dos sentores censitários) e a heterogenização da distribuição da renda na escala extena (entre dos sentores censitários) (Melazzo e Guimarães, 2010) resulta potencialmente em índices de desigualdade de renda contraditórios e/ou ineficientes. Primeiro, é potencialmente contraditório porque evidencia uma igualdade da distribuição da renda interna ao mesmo tempo que uma desigualdade da distribuição da renda externa. Segundo, é potencialmente ineficiente porque, ao criar uma distribuição de renda em que quase sempre há combinação de diferentes faixas de renda, pode reduzir artificialmente o índice de desigualdade de renda.

Para analisar os efeitos que a alteração da escala produz no índice pretendido, escolhemos a análise do índide de desigualdade de renda porque: i) é, em compração à multidimensionalidade dos indides de desigualdade social, mais fácil de tratar e analisar; ii) é tradicionalmente uma das variáveis mais utilizadas em pesquisas sobre a desigualdade social; iii) a compreensão das mudanças nos indíces de desigualdade de renda permite aprimorar a leitura e a correlação com outras dimensões e variáveis da vida social; iv) fornece elementos para pensar sistemas de indicadores que objetivem estudar as desigualdades sociais, tomadas de maneira ampla, e a segregação socioespacial (Caldeira, 2000; Correa, 1989; Sposito, 2011; Alves, 2018), na qual um dos elementos é a renda.

Lembra Correa (1989, p. 145) que “a segregação é um processo que origina a tendência a uma organização espacial em áreas de forte homogeneidade social interna e de forte disparidade social entre elas”. A partir disso podemos afirmar que a homogeneidade da composição de rendas numa mesma área e a heterogeneidade entre áreas, nossa preocupação central, são, por sua vez, elementos indicativos para a compreensão da segregação socioespacial, ainda que seja apenas uma parte desta última.

Os índices de desigualdade de renda podem ser derivados diretamente da curva de Lorenz, pois a renda é uma escala invariante, e as medidas derivadas da curva de Lorenz herdam essa propriedade (Jenkins, 1991). Em síntese, a curva de Lorenz representa uma distribuição relativa de uma variável em um determinado domínio (Lorenz, 1905).

Neri e Souza (2012) apontam que na análise da desigualdade de renda, a variável em perspectiva é o total de rendimento sob o domínio do número de pessoas, sendo a dimensão da desigualdade encontrada na curvatura da curva de Lorenz. Para Jenkins (1991), quando todos têm a mesma renda (igualdade perfeita), a curva de Lorenz seria na verdade uma reta de 45 graus, e quando toda a renda é de apenas uma pessoa (desigualdade completa), a curva seguiria todo o eixo horizontal. A curva de Lorenz representa a quantidade acumulada da renda em relação à quantidade acumulada da população.

Contudo, Jenkins (1991) destaca que a análise de desigualdade de renda mais comum não é pela curva de Lorez, e sim pelo coeficiente de Gini. Conforme Neri e Souza (2012), o coeficiente de Gini é a representação numérica de uma função de bem-estar e retrata uma relação de desigualdade de renda.

Neri e Souza (2012) mostram que o coeficiente de Gini pode variar entre 0 a 1, assumindo valor 0 quando há uma igualdade perfeita entre as variáveis, e valor 1 quando há desigualdade perfeita. O coeficiente de Gini, entre as variáveis renda e população, se aproximará de 1 quando houver uma concentração desproporcional da renda em relação à população, podendo ser obtido pela Fórmula 1.

 

 

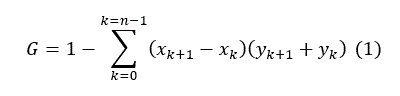
Onde:

G = coeficiente de Gini;

x  = proporção acumulada da variável população;

y = proporção acumulada da variável renda.

Maio (2007) destaca que o coeficiente de Gini tem sido o método mais popular de medida de desigualdade de renda. No entanto, existem vários métodos alternativos. Massey (2003) complementa que a medida de dissimilaridade, que é altamente correlacionada com o coeficiente de Gini, também é muito usada para medir a segregação, especialmente em relação ao espaço geográfico.

Alencar, Barroso e Abreu (2013) lembram que quantificar a dissimilaridade e/ou quantificar a similaridade é medir a distância entre elementos, constatar uma correlação dentro de um padrão, utilizar alguma medida para comparar os elementos, constatar ou não se um elemento (A) é mais parecido com (B) do que com (C), bem como definir um coeficiente que mensure a distância entre os elementos.

Massey (2003) utiliza a medida de dissimilaridade para analisar dados de renda das famílias norte-americanas em diversas escalas (bairros, municípios e estados), durante os períodos de 1950 a 2000, relacionando a desigualdade de renda a uma maior concentração da riqueza e/ou pobreza no espaço geográfico. A medida de similaridade ou coeficiente de dissimilaridade é calculada com base numa matriz de distâncias euclidianas, onde baixos coeficientes de dissimilaridade representam maiores proximidades, semelhança ou parecença entre os elementos, podendo os elementos com distâncias euclidianas mais próximas serem agrupados e visualizados graficamente em esquemas denominados dendrogramas (Alencar, Barroso e Abreu, 2013).

Massey (2003) avalia a dissimilaridade residencial entre ricos e pobres, medindo a distância entre as rendas das famílias localizadas nos dois extremos da distribuição de renda. Em síntese, esta medição representa o número relativo de famílias pobres e ricas que teriam de trocar de lugar para se obter uma distribuição de renda uniforme.

As medidas de dissimilaridade podem ser obtidas por meio de muitas técnicas e algoritmos. As técnicas hierárquicas de agrupamento são vantajosas, especialmente, durante a fase exploratória da análise, pois não exigem a indicação do número de agrupamentos. Além disso, a escolha do método pode gerar diferentes quantidades de grupos. Por exemplo, se comparados com outros métodos, o método Average Linkage produz grupos mais homogêneos, pois utiliza a média das distâncias entre todos os pares de objetos da matriz de dados para criar a matriz de distâncias, sendo, obviamente, mais apropriado para identificar diferenças entre grupos (Alencar, Barroso e Abreu, 2013).

De modo contrário, altos coeficientes de similaridade (coeficiente de correlação) indicam uma maior proximidade ou semelhança entre os elementos sob análise. Normalmente, os coeficientes de dissimilaridade são mais adequados para as variáveis quantitativas, e os de similaridade para as variáveis qualitativas, mas alguns coeficientes se adaptam melhor a determinadas situações de estudo e análise (Alencar, Barroso e Abreu, 2013).

A correlação é uma relação estatística que envolve duas ou mais variáveis, sendo o coeficiente de correlação a medida da relação destas variáveis aleatórias que pode, ou não, indicar uma relação de dependência e/ou causalidade (Gujarati, 2011).

Peters (2013) demonstra que a análise da desigualdade de renda pode ser examinada a partir de correlações entre variáveis socioeconômicas espacializadas, agrupadas ou não, por meio da regressão linear. A análise de desigualdade de renda aplicando correlações foi a técnica usada por Essletzbichler (2015) e Breau (2014) na identificação da aceleração do crescimento da renda acumulada dos 1% mais ricos da população dos Estados Unidos e das alterações nas características destas populações do Canadá.

Por exemplo, Peters (2013) correlaciona índices de desigualdade de renda às características das cidades norte-americanas. A desigualdade de renda está correlacionada com cidades maiores, mais ricas, com mais altos salários, serviços especializados em finanças, profissionais de alta qualificação e mineração baseada em energia. Por outro, a igualdade está correlacionada com cidades com serviços de baixa remuneração e/ou qualificação, lazer de baixo custo, educação e serviços de saúde de médio custo, atividades de manufatura e economias agrícolas estagnadas.

A força da correlação das variáveis pode ser medida pelo coeficiente de correlação  que é obtido pela divisão da covariância de duas variáveis pelo produto dos seus desvios padrão (Gujarati, 2011). O cálculo do coeficiente de correlação é apresentado pela Fórmula 2:

 

 

O coeficiente  pode variar entre um negativo e um (-1  1). Coeficientes iguais ou próximos a estes significam uma associação forte entre as variáveis, e coeficientes próximos a zero (0) significam uma associação fraca entre as variáveis. De modo geral, coeficientes abaixo de sete décimos negativos e acima de sete décimos (-0,7  0,7) significa que as variáveis têm um grau de associação ou dependência que pode indicar uma relação de causalidade. Por fim, o sinal positivo ou negativo do coeficiente  indica a direção da associação entre as variáveis (Hair et al., 2009).

A descrição dessa associação ou relação pode ser apresentada através de uma função matemática, sendo a regressão a técnica que determina os parâmetros dessa função (Oliveira, Dalmônica e Silva, 2011).

A regressão simples, ou regressão bivariada, é uma técnica que pode ser útil para prever qual seria o comportamento de uma variável dependente a partir do conhecimento de uma variável independente (Hair et al., 2009). Os métodos baseados em regressão multivariada podem ser úteis para prever qual seria o comportamento de uma variável dependente a partir do conhecimento de duas ou mais variáveis independentes, permitindo medir e prever a distribuições de renda a partir de variáveis de população e de rendimentos (Jenkins, 1991).

Neste sentido, se há correlação (dependência) entre a variável renda e as variáveis relacionadas às características observadas de cada indivíduo, esta correlação assumirá a forma de regressão linear. Assim, a renda será uma função das características de cada indivíduo mais um erro que resume os fatores não observáveis. Logo, a diferença da renda entre A e B poderão ser obtidas por meio da função linear que representa as diferenças das características observadas destes indivíduos (Jenkins, 1991).

Além das técnicas citadas, Maio (2007) relaciona outras medidas de desigualdade de renda: coeficiente de variação (desvio padrão da distribuição de renda pela sua média); razões de decil (feita tomando-se, por exemplo, a renda obtida pelos 10% das famílias e dividindo-a pela renda obtida pelos 10% mais pobres); índice Robin Hood (distância vertical máxima da curva de Lorenz à linha de igualdade); medida de pobreza Sen (incorpora o coeficiente de Gini para pessoas abaixo da linha de pobreza, juntamente com a taxa de incidência da pobreza e a renda média daqueles abaixo da linha de pobreza); e índice de Atkinson (permite uma sensibilidade variável às desigualdades em diferentes partes da distribuição de renda).

O índice de entropia generalizada, o índice de progressividade kakwani e a proporção de renda total auferida também são medidas aplicáveis para análise da desigualdade de renda. Contudo, como mostram Kawachi e Bruce (1997), estas medidas se comportaram de forma muito semelhante e são geralmente fortemente correlacionadas . Por isso, investigamos a curva de Lorenz e coeficiente de Gini em diferentes escalas, nos aprofundando na análise da escala intraurbana aplicando as técnicas de dissimilaridade, correlação e regressão.

 

 

3. Materiais e métodos

Nesta pesquisa, são realizados cálculos para medir a desigualdade da distribuição da renda nas escalas geográficas do Estado do Paraná, Área urbana de Maringá e Setores Censitários Urbanos da cidade de Maringá, e cálculos para compreender em detalhe a desigualdade da distribuição da renda intraurbana. A cidade de Maringá está localizada na região norte do Paraná (Mapa 1) e constitui-se em uma das cidades mais importes do Estado do Paraná que, conforme os estudos do IBGE (2007, 2017), desempenha importantes papéis no ambito da rende urbana.

 

 

Após as etapas de (1) coleta de dados e (2) pré-processamento de dados, calculamos a (3) desigualdade de renda pela curva de Lorenz; e (4) desigualdade de renda pelo coeficiente de Gini; em seguida, na escala intraurbana, calculamos: (5) a dissimilaridade da distribuição da renda externa (entre setores censitários); (6) a desigualdade de renda interna (dentro dos setores censitários) por correlação linear; (7) a função de desigualdade de renda por regressão, por meio dos softwares Ninna Cluster e Microsoft Excel; (8) Após o tratamento estatísitco, passou-se à espacializaçãos dos dados através da representação cartográfica com o uso do software Qgis, com a produção de dois mapas coropléticos, e, por fim; 9) análise dos resultados, quando procuramos fazer alguns apontamos acerca da configuração espcial  da desigualdade de renda no espaço intraurbano.

 

3.1. Coleta e pré-processamento de dados

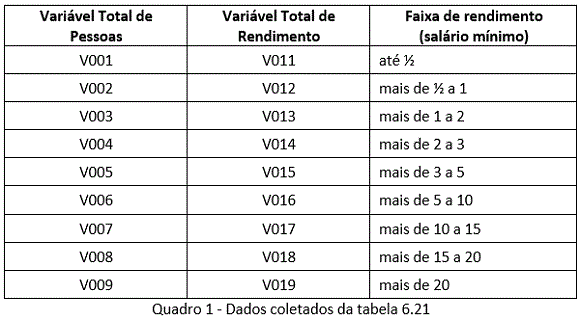
Para a realização dos cálculos foi utilizada a base de microdados agregados, por setor censitário, do Paraná, do censo 2010 (IBGE, 2010). Em especial, foram utilizadas as Tabelas 6.2 (Básico) e 6.21 (arquivo renda da pessoa). No Quadro 1 são identificadas as variáveis da tabela 6.21, consistindo-se no número e no rendimento total das pessoas de 10 anos ou mais de idade, por faixa de rendimento.

 

 

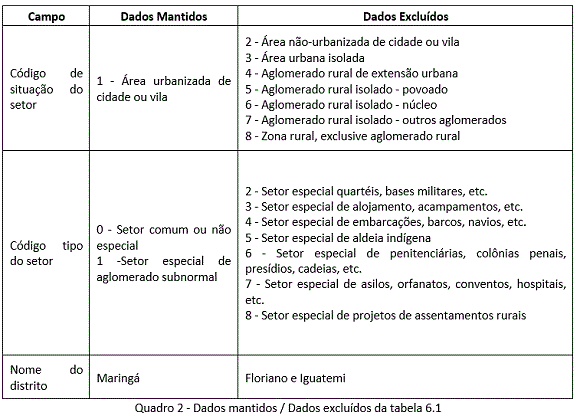
A etapa de pré-processamento de dados envolve as ações de seleção, tratamento e separação dos dados. Na ação de seleção, apenas os dados que fazem parte da análise são mantidos. No Quadro 2 são identificados os dados que foram mantidos ou excluídos da tabela 6.1.

 

 

Na ação de tratamento de dados é feita a associação das tabelas com os dados selecionados, criando uma tabela que contém apenas as informações e os setores censitários foco da análise. Neste caso, os dados dos setores censitários do estado do Paraná. Para finalizar a ação de estruturação, em alguns casos foi preciso excluir os setores censitários com dados faltantes, representados por “X”.

Por fim, na ação de separação dos dados, a tabela obtida nas ações anteriores é duplicada e filtrada pelo campo “nome do município”, que neste caso foi Maringá. Como resultado disso, os dados dos setores censitários urbanos da cidade de Maringá, envolvendo os setores de número 411520005000001 a 411520015330007, estão separados e prontos para os cálculos de desigualdade de renda.

 

3.2. Cálculos da desigualdade de renda (Lorenz; Gini; Dissimilaridade; Correlação; e Regressão)

Para encontrarmos a curva de Lorenz e o Coeficiente de Gini foram realizados os seguintes cálculos iniciais: renda total por setor censitário; população por setor censitário; população total por faixa de rendimento; rendimento total por faixa de rendimento; proporção da população total por faixa de rendimento; proporção da renda total por faixa de rendimento; proporções acumuladas da renda R e da população P.

A curva de Lorenz é elaborada a partir dos pares de valores R x P, ou seja, a proporção acumulada da renda total e a proporção acumulada da população, onde o primeiro par de valores representa a faixa de menor renda. Assim, o gráfico é representado no eixo x pelos valores de P e no eixo y os valores de R. Destaca-se que, para fins de comparação, utilizamos para os valores de x a distribuição da população do Estado do Paraná. Por fim, se elabora a curva de igualdade, inserindo no eixo x e y os valores da interpolação linear obtida dex_a=a(1/n),a=0,1...,n, onde n é o número de valores interpolados (n=9), somando, a cada variação de x o valor de a=0,111.

Com os valores da proporção acumulada da variável população (P) e da soma proporção acumulada da variável renda (R), obtidos nos cálculos iniciais, calculamos o coeficiente de Gini, aplicando a Fórmula 1. Assim, o coeficiente de Gini se aproximará de 1 quando houver uma concentração desproporcional da renda em relação à população, e se aproximará de 0 quando houver uma distribuição perfeita da renda para a população.

Com a curva de Lorenz e o coeficiente de Gini pode-se analisar e comparar o comportamento das variáveis (faixas de renda) para a mesma unidade de análise (área urbanda de Maringá) em duas escalas geográficas distintas (urbana e intraurbana), e observar os efeitos que a alteração da escala produz nos índices de desigualdade de renda.

Para compreender o efeito desta alteração, analisamos o comportamento da própria variável (faixas de renda) dentro do conjunto de dados. Tal comportamento está relacionado ao padrão da variação da proporção população em cada nível de renda. Para isso, aplicamos as técnicas estatísticas de dissemelhança (agrupamento por distância) e semelhança (correlação) para avaliar o comportamento das variáveis.

A dissemelhança entre variáveis (faixas de renda) é calculada a partir da média das distâncias euclidianas da matriz gerada por meio de algoritmo hierárquico. Com isso, cada uma das variáveis (faixas de renda) pode ser observada e relacionada com outra variável a partir da distância. Assim, quanto maior a distância entre as variáveis maior será sua dissemelhança (diferença) em relação ao comportamento da variável. Em síntese, a técnica permite identificar quais as variáveis (faixas de renda) têm sua variação de proporção de população diferentes e quais têm um comportamento parecido. Essa identificação é realizada analisando o gráfico de dendrograma (Alencar, Barroso e Abreu, 2013).

Em sentido oposto, a semelhança do comportamento das variáveis é calculada a partir do coeficiente de correlação linear, aplicando a Fórmula 2. Com isso, um coeficiente R próximo de +/-1 retratará uma forte associação entre duas variáveis (faixa de renda), tendo como base o comportamento desse mesmo par de variáveis no conjunto dos setores censitários em estudo. De modo contrário, quando R for próximo de 0 (zero), poderemos afirmar que o comportamento do par de variáveis é fracamente associado, ou que não há semelhança no comportamento das variáveis. Para essa análise, consideraremos que valores de R entre 70% a 90% (positivo ou negativo) indicam uma correlação forte entre variáveis (Hair et al., 2009). Onde valores de R próximos de +/-1 retratam uma associação forte entre duas faixas de renda, possibilitando identificar se a presença de uma variável α implica na presença de uma variável β (+1) ou na ausência de uma variável ω (-1). Por outro lado, valores de R próximos de 0 retratam a inexistência de associação entre duas variáveis, permitindo afirmar que a presença da variável α não está associada à presença de β ou à ausência de ω.

Assim, analisando cada uma das variáveis sob o contexto das hipóteses de correlação acima descritas, conseguimos avaliar as relações entre cada uma das variáveis nos setores censitários. Por exemplo, se há forte correlação entre α e β, sendo esta positiva, podemos afirmar que a presença de α em um setor censitário implica na presença de β; e caso a correlação entre α e ω seja forte e negativa, quanto maior for a presença de α no setor censitário, menor será a presença de ω. Em última análise, se a correlação ente α, β ou ω e Ω for fraca (R≅0), então poderemos afirmar que a presença de Ω no setor censitário não está relacionada com a presença ou ausência das variáveis α, β ou ω.

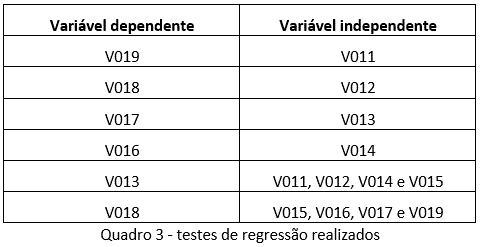
Para verificar a significância estatística dos coeficientes de correlação, avaliar como as variáveis estão associadas e mensurar o coeficiente e os pesos dessas associações é realizada a regressão. Neste caso, estas regressões e suas variáveis são representadas no Quadro 3.

 

 

Por fim, os resultados obtidos são utilizados para criar as funções de determinação da população por faixa de renda, conforme os dados dos setores censitários.

 

 

4. Resultados e discussão

No Gráfico 1 verifica-se a relação das desigualdades de renda em diferentes escalas de observação. O alargamento da curva em direção ao eixo  retrata uma concentração de renda. A área entre a curva e a reta de 45 graus mostra a magnitude da desigualdade de renda, tendo como base a distribuição da população do Estado do Paraná.

 

 

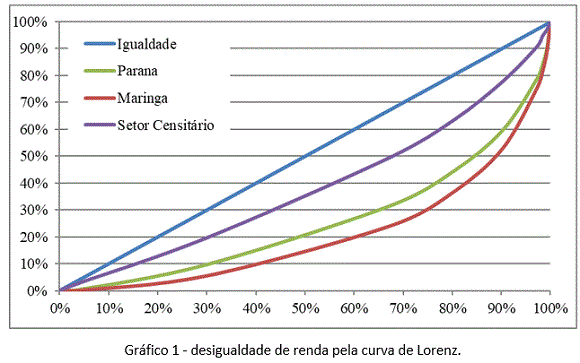
O padrão de distribuição de renda nos setores sencitários urbanos da cidade de Maringá é a curva que mais se aproxima da igualdade. De certo modo, podemos falar que tal distribuição de renda esconde desigualdades externas (entre setores censitários).

Portanto, a desigualdade de renda nos setores censitários é heterogênea (entre setores), ao mesmo tempo que é homogênea (dentro de si). Esta contradição causa um efeito (distorção) de redução no índide de desigualdade de renda e prejudica/impede a comparação deste índice de diferentes escalas. Por outro lado, a intensidade desta distorção representará o grau da desigualdade de renda intraurbana. Em outras palavras, quanto maior for a distorção entre as curvas de desigualdade de renda nas escalas urbana e intraurbana, maior será a desigualdade de renda na escala intraurbana. Ou então, quanto mais próxima forem as curvas de desigualdade, menor será a desigualdade de renda intraurbana.

Isto ocorre porque a curva de Lorenz do município e do estado é baseada em dados de renda agrupados. Agrupando as pessoas conforme sua faixa de renda, concentram-se os iguais e separam-se os desiguais, acentuando e destacando a desigualdade intraurbana. Em outras palavras, seria o mesmo que agrupar as famílias conforme sua renda em locais diferentes. Por isso, o gráfico pode não representar adequadamente toda a realidade.

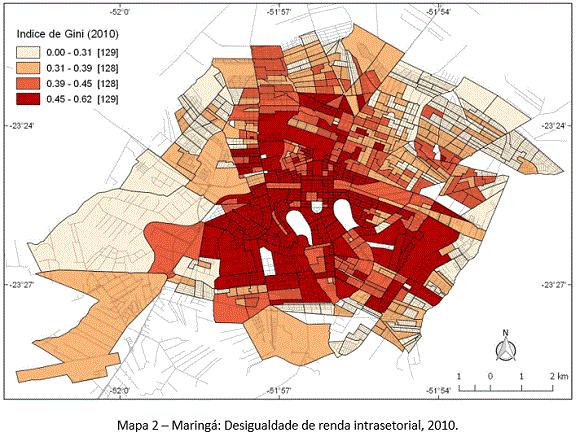
Além disso, é importante destacar que desigualdade de renda e desigualdade social são conceitos distintos, pois, associamos desigualdade de renda às diferenças e pobreza ao nível de renda. Neste sentido, uma menor desigualdade de renda entre setores censitários pode não significar menores níveis de desigualdade social, pois a desigualdade social deve envolver variáveis para além da variável de distribuiçao da renda. De qualquer modo, a medida de desigualdade de renda calculada pelo coeficiente de Gini retrata a dinâmica das diferenças dos níveis de renda dentro dos setores censitários urbanos da cidade de Maringá. Como é possível verificar no Mapa 2, os setores classificados como mais desiguais em termos de renda estão contíguos ao centro da área urbana, indicando uma composição de renda mais heterogênea internamente. Isso quer dizer que a amplitude da renda é maior, comportando desde os rendimentos mais baixos até os mais elevados.

 

 

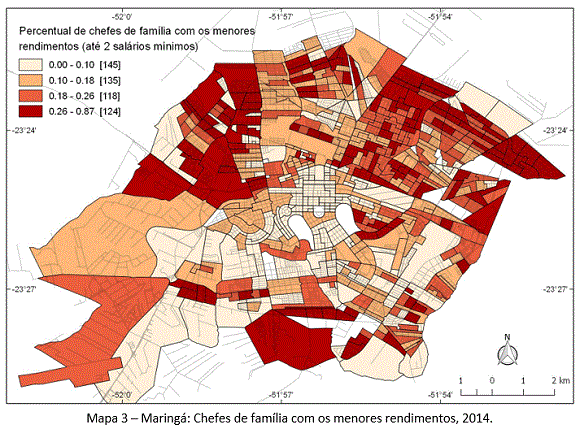
O Mapa 3, por sua vez, como complemento ao primeiro mapa, indica que os setores censitários como os mais baixos salários da cidade não correspondem aos setores com as maiores desigualdades de renda internas. Em complemento, ao que dissemos anteriormente, é a evidência de que desigualdade de renda não se confunde com desigualdade social. Sinteticamente podemos afirmar que no caso de Maringá, uma cidade média do interior do estado do Paraná, os setores mais ricos são os mais heterogêneos (com maior desigualdade), enquanto que os setores mais homogêneos (com menor desigualdade) correspondem àqueles que concentram a população com os menores rendimentos. Aqui, portanto, podemos encontrar alguns elementos explicativos para o fato de que a desigualdade de renda em Maringá, tomada como um todo, é maior que a desigualdade de renda média constatada internamente nos setores censitários.

 

 

Em contexto, a Quadro 4 permite comparar os coeficientes de Gini calculados para cada uma das escalas de análise da pesquisa.

 

 

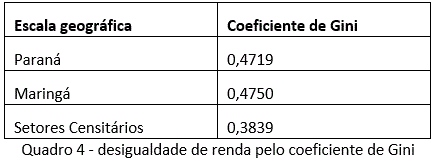
O coeficiente de Gini 0,3839 indica que a desigualdade na distribuição de renda e pessoas dentro dos setores censitários é relativamente baixa.

O Gráfico 2 traz os níveis de renda mais semelhantes nos setores censitários urbanos de Maringá. Nesse caso, a semelhança está relacionada à concentração e o padrão de associação de um determinado nível de renda dentro do conjunto de setores censitários.

 

 

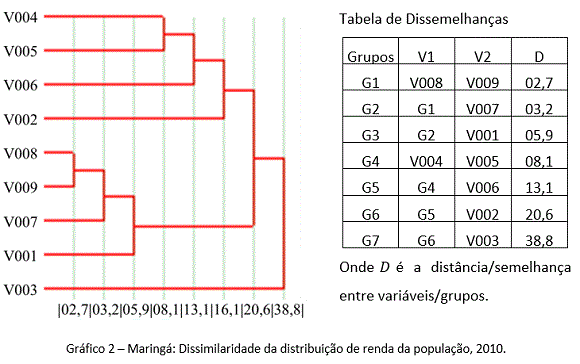
Um par de variáveis (nível de renda) semelhantes, ou menos distantes entre si, é que tem uma distribuição da população intra e entre setores também parecida. Por exemplo, no conjunto dos setores censitários, a população da variável V008 está proximamente tão concentrada e/ou tão distribuída quanto a população da variável V009. Por outro lado, o Grupo 4 (variáveis V004 e V005) tem um comportamento não tão semelhante, ou seja, tais variáveis possuem um comportamento relativamente diferente. Neste caso, o padrão da distribuição da população das variáveis do V004 é diferente do padrão de distribuição da variável V005 nesta mesma unidade de análise.

Podemos destacar no gráfico que o agrupamento de variáveis V008-V009 é aquele que tem comportamento mais parecido. Isto implica em dizer que as populações nestes níveis de renda têm um padrão muito parecido à sua distribuição espacial. Além da análise de variáveis (faixas de renda), podemos comparar grupos. Assim, o comportamento espacial da variável G2 (altos níveis de renda) pode ser comparado com a variável V001 (faixa de renda mais baixa), e mostrar que apesar da grande diferença de renda, estas variáveis tem um comportamento espacial semelhante.

Para comprovar a dimensão de desigualdade de renda, analisam-se os coeficientes R do Quadro 5. Estes coeficientes representam a associação das faixas de renda e sua distribuição geográfica (setor censitário). Altos índices de coeficientes R podem ser interpretados como a existência de um padrão da distribuição de renda dentro dos setores censitários.

 

 

Por exemplo, como o valor de R da associação entre V018 e V019 (89%) se aproxima de 1, significa que a presença de pessoas com renda acima de 20 salários está associada geograficamente (setores censitários) à presença de pessoas com rendimento ente 15 e 20 salários.

Por outro lado, como o valor de R da associação de V011 com V019 (-0,23%) se aproxima de 0 (zero), significa que, considerando o conjunto de setores censitários de Maringá, a presença de pessoas com renda acima de 20 salários não está associada geograficamente (setores censitários) a pessoas com renda de até 1/8 salários.

Analisando o padrão da distribuição de renda entre os estratos de renda mais baixos (V11 com V12 e V13), observamos altos valores de R 72%, 70%, e (V12 com V13) 88% sugerindo que alguns setores censitários são formados majoritariamente por estas três faixas de renda. Comparados à faixa de renda V014, por sua vez, os coeficientes Rcaem significativamente (44%, 57% e 78%).

Neste sentido, tendo os setores censitários de Maringá como o espaço geográfico de análise da desigualdade de renda, vemos que o padrão da distribuição de renda é positivo, mas restrito às faixas de renda próximas. Desta forma, temos um espaço intraurbano formado por setores censitários que são constituídos, majoritariamente, por pessoas de faixas de renda próximas e pela presença aleatória de pessoas de faixas de renda distantes. Neste último caso, onde existe uma presença aleatória entre pessoas de rendas distantes, tal associação é sempre negativa. Assim, mesmo que a relação entre faixas de renda distantes não tenha um padrão, quanto maior o número de pessoas de uma faixa de renda, menor será o número de pessoas da outra faixa de renda.

As dinâmicas próprias da produção do espaço urbano e os agentes que disputam a cidade de modo permanente (Carlos, Souza e Sposito, 2011; Carlos, Santos e Alvarez, 2018) produzem uma morfologia urbana caracterizada pela separação das classes sociais que tem reflexo direto na composição das rendas nos setores censitários. A própria ação do Estado, como um dos agentes importantes no processo de produçao do espaço urbano, através da implementação de políticas habitacionais (Santo Amore, Shimbo e Rufino, 2015), contribui para produzir maior homogeneidade das rendas no interior dos setores censitários, pelo agrupamento de famílias com rendas semelhantes.

Em síntese, a presença da homogeneidade interna (concentração de pessoas de faixas de renda próximas) e da heterogeneidade extena (separação de pessoas de faixas de rendas distantes) é confirmada tanto pela medida de dissimilaridade quanto pela medida de similaridade.

Porém, algumas vezes, a associação entre as variáveis acontece por acaso, resultando em coeficientes de correlação com baixa significância estatística. Além disso, o coeficiente R mostra força de associação entre as variáveis, mas não mostra qual é esta associação.

Para garantir a consistência dos cálculos e das análises da desigualdade de renda calculada pelo coeficiente de Gini e pela correlação linear, analisamos os resultados da aplicação da técnica de regressão linear. Estes resultados, contendo as variáveis dependentes e independentes, seus respectivos coeficientes de correlação R, significação estatística da associação (F de significação) e a significância entre as variáveis (Valor-p), são apresentados no Quadro 6.

 

 

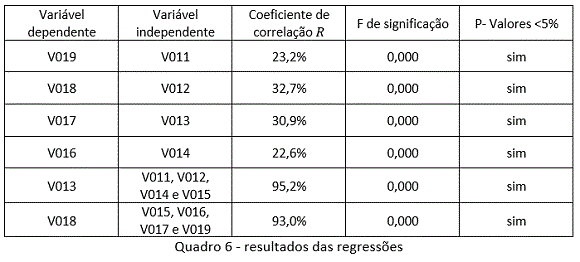
Os valores F de significação e P-valores praticamente iguais a 0 (zero), significam que a regressão e a significância das variáveis são expressivas. Em todos os casos, os cálculos são estatisticamente válidos. Logo, é possível afirmar que os resultados obtidos pela correlação linear não ocorrem por acaso. E, a partir das variáveis independentes, é possível estimar o valor da variável dependente.

Contudo, para afirmarmos que existe uma associação explicativa entre as variáreis, é preciso que sua correlação também seja significativa. Neste caso, não observamos correlações fortes suficientes nas primeiras 4 tentativas de associação (regressões). Em verdade, os coeficientes encontrados, naturalmente, são os mesmos daqueles obtidos no cálculo de correlação linear. Neste caso, a regressão comprova, a partir do F de significação, que a associação entre faixas de renda distantes nos setores censitários, realmente, não acontece. Ou seja, quando as faixas de renda são distantes, quanto pior forem o resultados da associação entre rendas, maior será a desigualdade de renda externa.

Por outro lado, as duas últimas tentativas de associação (regressões) têm coeficientes de correlação muito significativos, acima de 90%. Logo, é possível, por exemplo, estimar V018 (faixa de renda com rendimento de 15 a 20 salários), com uma probabilidade de 93% de acerto. Neste caso, a quantidade de pessoas V018 do setor censitário escolhido é uma função formada pelos valores das variáveis (V015, V016, V017 e V019) e seus respectivos coeficientes aprestados no Quadro 7.

 

 

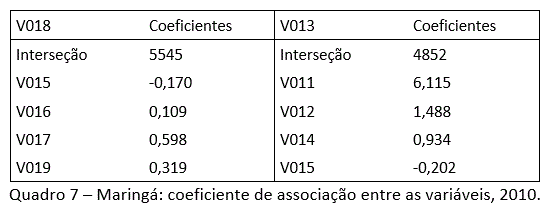
Seguindo o exemplo, 〖V_018〗_i ou o rendimento total da faixa de renda com rendimento de 15 a 20 salários, do setor censitário investigado i pode ser estimado pela função: 〖V_018〗_i=-0,17 〖V_015〗_i+0,109〖V_016〗_i+〖0,598V_017〗_i+〖0,319V_019〗_i+5545. Onde os coeficientes da equação representam o peso de cada faixa de renda e V_i é o valor da variável independente no setor censitário investigado i.

Vale destacar que, as variáveis V017 e V011 têm maior peso nas estimativas de V018 e V013, respectivamente. Em outras palavras, o número de pessoas da faixa de renda com rendimento de 15 a 20 salários e de mais de 1 até 2 salários (V018 e V013) de um setor censitário investigado i, será obtido, principalmente, pelo número de pessoas das faixas de renda com rendimento de mais de 10 até 15 salários e de 0 até ½ salário (V017 e V011) deste setor censitário, conforme seus respectivos coeficientes 0,60 e 5,91.

Se por um lado, a aplicação da regressão comprova que as faixas de renda distantes estão fracamente associadas dentro dos setores censitários, comprova também que esta associação é inversa, ou, negativa (V015). E, que existe uma associação forte entre faixas de renda próximas. No contexto, estes resultados sugerem uma forte homogeneidade nos setores censitários ou, em outras palavras, alta igualdade de renda interna. Esta igualdade resulta na separação do espaço urbano, representado pelos setores, das pessoas conforme sua faixa de renda.

Para exemplificar que a separação se dá conforme a geografia da renda, que concentra no interior de cada área do espaço urbano faixas de renda parecidas, vemos que a correlação entre faixas de renda em torno da variável V013 é alta e estatisticamente significativa. Mas, que as variáveis do entorno de V013 têm como característica pessoas de faixa de rendimento baixo. Logo, não encontraremos desigualdade de renda, e sim a concentração de pessoas de baixa renda, e que a determinante da desigualdade de renda é a presença ou não de concentração de pessoas de alta renda em outros espaços urbanos.

 

 

5. Conclusão

Análises sobre a desigualdade de renda produzidas pela aplicação dos mais diversos métodos de medição, têm se dedicado principalmente à comparação das diferenças entre grupos dentro de uma mesma unidade espacial, desconsiderando os efeitos que a escala pode gerar nos índices gerados, e logo, na análise destes índices.

Mostramos que as especificidades das unidades de análise estudadas dificultam a comparação dos resultados obtidos por diferentes métodos e que a ausência de análises da desigualdade de renda dentro dos grupos de análise dificulta a compressão de como esses mesmos grupos se distribuem internamente.

Os diferentes métodos de medição da desigualdade de renda aplicados para tratar e capturar a natureza das desigualdades de renda intraurbanas produzem, na verdade, resultados relacionados e complementares. De modo geral, a homogeneidade dos setores censitários, ou agrupamento de populações semelhantes em áreas comuns, tende a reduzir os índices de desigualdade de renda interna. Essa característica mostra que a escala influencia na medida de desigualdade de renda.

Essas evidências empíricas mostram que altos níveis de desigualdade de renda podem ser ocultados à medida que a escala espacial se altera. Para uma mesma cidade, o nível de desigualdade de renda pode ser reduzido em 19% quando a escala de análise é alterada (de região urbana para setores censitários urbanos). Enquanto escalas de análise maiores (estado ou município) trazem medidas de desigualdade de renda mais precisas, escalas menores (setores censitários) proporcionam uma melhor visão da distribuição da desigualdade de renda.

As distorções nos índices de desigualdade de renda provocadas pela alteração da escala mostram que a comparação destes em diferentes escalas pode gerar análises equivocadas, ao mesmo tempo que a intensidade destas distorções pode ser usada para se inferir o grau da desigualdade de renda intraurbana.

Estes resultados podem contribuir para novas discussões sobre a desigualdade de renda no espaço geográfico, especialmente nas cidades brasileiras. Diferenças de renda intrasetoriais não significativas, na medida em que produzem, em contextos urbanos, maiores diferenças de renda intersetoriais, tem potencial para refinar a compreensão da desigualdade de renda intraurbana. Esses resultados também podem ser considerados na proposição de sistemas de indicadores sociais e associados com índices de desigualdade social multidimensionais em pesquisas futuras em diferentes aplicações.

 

 

6. Referências bibliográficas

ALENCAR, B. J. ; BARROSO, L. C. ; ABREU, J. F. Análise Multivariada de Dados no Tratamento da Informação Espacial: uma abordagem com análise de Agrupamentos. Revista Iberoamericana de Sistemas, Cibernética e Informática, 2013, v.10, n. 2 p. 6-12.         [ Links ]

ALVES, G. A. As centralidades periféricas: da segregação socioespacial ao direito à Cidade. In: CARLOS, A. F. A; SANTOS, C. S; ALVAREZ, I. P. Geografia urbana crítica. Contexto: São Paulo, 2018, p. 109-2124. ISBN 13: 97-885-5200-064-8        [ Links ]

AMARANTE, Verónica; COLACCE, Maira. More unequal or less? A review of global, regional and national income inequality. CEPAL Review, 2018, n. 24, p. 1-30.         [ Links ]

ARRETCHE, M. Trajetórias das desigualdades. São Paulo: Editora Unesp, 2015. ISBN 97-885-3930-566-7.         [ Links ]

BOBBIO, N. Direita e esquerda. São Paulo: Editora Unesp, 2011. ISBN: 978-85-3930-081-5.         [ Links ]

BREAU, Sébastien. The Occupy Movement and the top 1% in Canada. Antipode, 2014, v. 46, n. 1, p. 13-33.         [ Links ]

CALDEIRA, T. P. Cidade de muros. São Paulo, Edusp, 2000. ISBN-13: 97-885-7326-188-2.         [ Links ]

CARLOS, Ana Fani Alessandri. O lugar no/do mundo. São Paulo: Hucitec, 1996. ISBN 978-85-7506-143-5.         [ Links ]

CASTRO, Iná Elias de. O problema da escala. IN: CASTRO, Iná Elias de; GOMES, Paulo Cesar da Costa; CORRÊA, Roberto Lobato (Orgs). Geografia: conceitos e temas. Edição 17. Rio de Janeiro: Bertrand Brasil, 2017. ISBN 13: 97-885-2860-545-7.         [ Links ]

CORREA, Roberto L. O espaço urbano. São Paulo: Ática, 1989.         [ Links ]

CRUZ LIMA, Ana Carolina; SIMÕES, Rodrigo; MONTE-MÓR, Roberto de Melo Luís. Espaço, cidades e escalas territoriais: novas implicações de políticas de desenvolvimento regional. Economia e Sociedade, Campinas, abr. 2014, v. 23, n. 1 (50), p. 223-242.         [ Links ]

DOWBOR, L. O que faz a economia funcionar? Revista de Desenvolvimento e Políticas Públicas, Viçosa, 2017, v. 1, n. 2, p. 154-169.         [ Links ]

ESSLETZBICHLER, Jürgen. The top 1% in US metropolitan areas. Applied Geography, 2015, v. 61, p. 35-46.         [ Links ]

GEORGE, Pierre. Questions de morphologie urbaine et d'aménagement des villes. In: Annales de Géographie. Armand Colin, 1958. p. 57-59.         [ Links ]

GUJARATI, Damodar N.; PORTER, Dawn C. Econometria Básica-5. Amgh Editora, 2011. ISBN 978-85-6330-832-0.         [ Links ]

HAIR, J. F. BLACK, B. BABIN, B. ANDERSON, R. TATAN, R. Análise Multivariada de Dados. 6ed. Porto Alegre. Artmed Editora. 2009. ISBN 978-85-7780-402-3.         [ Links ]

HOFFMANN, Rodolfo. Medidas de polarização da distribuição da renda e sua evolução no Brasil de 1995 a 2013. Economia e Sociedade, 2017, v. 26, n. 1, p. 165-187.         [ Links ]

IBGE, Instituto Brasileiro de Geografia e Estatística. Atlas do Censo Demográfico 2010. [online]. Brasil, 2010. [consultado 19 dezembro 2016]. Disponível na World Wide Web: http://www.ibge.gov.br.         [ Links ]

IBGE, Instituto Brasileiro de Geografia e Estatística. Divisão regional do Brasil em regiões geográficas imediatas e regiões geográficas intermediárias. IBGE/Coordenação de Geografia: Rio de Janeiro, 2017. ISBN-13: 97-885-2404-418-2        [ Links ]

IBGE, Instituto Brasileiro de Geografia e Estatística. Regiões de influência das cidades 2007. IBGE: Rio de Janeiro, 2008. ISBN-10:  85-240-0752-4        [ Links ]

JANNUZZI, P. (I)ndicadores sociais no Brasil. 5. ed. São Paulo: Alínea, 2012. ISBN-13: 97-885-7516-807-3.         [ Links ]

JENKINS, Stephen. The measurement of income inequality. Economic Inequality and Poverty, 1991, p. 3-31.         [ Links ]

KAWACHI, I; BRUCE P. K. The relationship of income inequality to mortality: does the choice of indicator matter? Social science & medicine, 1997, v.45, n.7 p.1121-1127.         [ Links ]

KOGA, D. H. Medidas de cidades: entre territórios de vida e territórios vividos. São Paulo: Cortez, 2003. ISBN-13: 97-885-2490-936-8.         [ Links ]

LINDO, Paula V. de Faria. Geografia e política de assistência social: territórios, escalas e representações cartográficas para políticas públicas. São Paulo: Cultura Acadêmica, 2011. ISBN-13: 978-85-7983-196-6.         [ Links ]

LOPES JÚNIOR; DOS SANTOS, Wilson Martins; DOS SANTOS, Regina Célia Bega. Reprodução do espaço urbano e a discussão de novas centralidades. Raega- O Espaço Geográfico em Análise, 2010, v. 19.         [ Links ]

LORENZ, Max O. Methods of measuring the concentration of wealth. Publications of the American statistical association, 1905, v. 9, n. 70, p. 209-219.         [ Links ]

MAIO, F.G. Income inequality measures. Journal of Epidemiology & Community Health, 2007, v.61, n.10 p., 849-852.         [ Links ]

Massey, D. S.; Fischer, M. J.; Dickens, W. T.; Levy, F. The geography of inequality in the United States, 1950-2000 [with comments]. Brookings-Wharton papers on urban affairs, 2003, p. 1-40.         [ Links ]

MELAZZO, E. S.; FERREIRA, Júlio; MIYAZAKI, Vitor. Renda e desigualdades no espaço intra-urbano de Presidente Prudente: uma análise empírica dos resultados dos Censos 1991 e 2000. Caderno Prudentino de Geografia, 2003, v.25, p.209-223.         [ Links ]

MELAZZO, E. S.; GUIMARÃES, R. B. Exclusão social em cidades brasileiras: um desafio para as políticas públicas. São Paulo: Editora da UNESP, 2010. ISBN 978-85- 7139-908-2.         [ Links ]

MELAZZO, Everaldo S.; CASTRO, Cloves A. A Escala Geográfica: Noção, Conceito ou Teoria? Terra Livre, 2015, v. 2, n. 29, p. 133-142.         [ Links ]

NERI, M.; SOUZA, P. H. C. F. A década inclusiva (2001-2011): desigualdade, pobreza e políticas de renda. Ipea: Brasília, 2012.         [ Links ]

OLIVEIRA, Antonio Marcos Machado; DALMÔNICA, Alice Henrique; SILVA, Mariana Mendes. Representação gráfica e cartográfica das desigualdades regionais no âmbito educacional das escolas públicas no estado de Minas Gerais. Boletim de Geografia, 2011, v. 29, n. 2, p. 75-92.         [ Links ]

OXFAM, Oxford Committee for Famine Relief. A distância que nos une: um retrato das desigualdades brasileiras. [Online]. Brief Comunicação, 2017. [consultado 06 maio 2018]. Disponível na World Wide Web: http://www.oxfam.org.br/sites/default/files/arquivos/Relatorio_A_distancia_que_nos_une.pdf.         [ Links ]

PETERS, David J. American income inequality across economic and geographic space, 1970–2010. Social science research, 2013, v. 42, n. 6, p. 1490-1504.

PIKETTY, T. Economia da desigualdade. Rio de Janeiro: Intrinseca, 2015. ISBN: 978-85-8057-648-1.         [ Links ]

PNUD (Programa das Nações Unidas para o Desenvolvimento). Desenvolvimento Humano para além das médias. Brasília: PNUD/IPEA/FJP, 2017. ISBN: 978-85-88201-45-3.         [ Links ]

SANTO AMORE, C., SHIMBO, L. Z., RUFINO, M. B. C. Minha casa... E a cidade? Avaliação do programa minha casa minha vida em seis estados brasileiros. Rio de Janeiro: Letra Capital, 2015. ISBN-13:  97-885-7785-377-9.         [ Links ]

SANTOS, M. O espaço do cidadão. 7. ed. São Paulo: Edusp, 2007. ISBN 10: 853-14-0971-3.         [ Links ]

SEN, Amartya. O desenvolvimento como expansão de capacidades. Lua Nova: revista de cultura e política, 1993, n. 28-29, p. 313-334.         [ Links ]

SILVEIRA, Leonardo Souza; MUNIZ, Jerônimo Oliveira. Intra-and inter-metropolitan variations of racial income inequality. Cadernos Metrópole, 2014, v. 16, n. 31, p. 265-289.         [ Links ]

SPOSATI, A. (Coord.) Mapa da exclusão/inclusão social da cidade de São Paulo. São Paulo: EDUC, 1996. ISBN-13: 978-85-2830-093-2.         [ Links ]

SPOSITO, M. E. B. A produção do espaço urbano: escalas, diferenças e desigualdades socioespaciais. In: CARLOS, A. F. A; SOUZA, M. L; SPOSITO, M. E. B. A produção do espaço urbano: agentes e processos, escalas e desafios. Contexto: São Paulo, 2011, p. 123-145. ISBN-13: 97-885-7244-633-4.         [ Links ]

STIEGLITZ, J. E. O preço da desigualdade. Lisboa: Bertrand Editora, 2016. ISBN: 9789722525589.         [ Links ]

VILLAÇA, Flávio. Espaço intra-urbano no Brasil. São Paulo: Studio nobel, 1998. ISBN-13: 978-85-7553-075-7.         [ Links ]

WEBSTER, Thomas J. Managerial economics: theory and practice. Elsevier, 2003. ISBN-10: 012-74-0852-5.         [ Links ]

 

 

7. Agradecimentos

O presente trabalho foi realizado com o apoio: i) da Coordenação de Aperfeiçoamento de Pessoal de Nível Superior - Brasil (CAPES) - Código de Financiamento 001; e ii) do Conselho Nacional de Desenvolvimento Científico e Tecnológico do Brasil (CNPq): a) Processo 423443/2016-0 - "Mapeamento e análise das desigualdades territoriais em cidades de porte médio do interior do Paraná" - Edital Universal 001/2016; e b) Bolsa de Produtividade, Grant 311032/2016-8.