Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Similares em
SciELO
Similares em
SciELO
Compartilhar
Tourism & Management Studies
versão impressa ISSN 2182-8458
TMStudies vol.11 no.1 Faro jan. 2015
TOURISM – RESEARCH PAPERS
Exponential forecasting of the monthly volume of the tourism receipts in Bulgaria
Previsão exponencial do volume mensal de receitas turísticas na Bulgária
Preslav Dimitrov1; Maria Kalinova2; Gantcho Gantchev3; Chavdar Nikolov4
1South-West University «Neofit Rilski», 2 Krali-Marko Str., Blagoevgrad 2700, Bulgaria, preslav.dimitrov@swu.bg
2South-West University «Neofit Rilski», 2700 Blagoevgrad, Bulgaria, maria.kalinova@ccbank.bg
3South-West University «Neofit Rilski», 2700 Blagoevgrad, Bulgaria, gantchev@swu.bg
4South-West University «Neofit Rilski», 2700 Blagoevgrad, Bulgaria, chavdarnikolov@abv.bg
ABSTRACT
In Compliance with the annual Act for the State Budget, the Bulgarian Ministry of Finance usually makes twice a year an internal budget restructuring in the budgets of the separate Ministries and State Agencies of the Bulgarian State. What is in intriguing in this internal budget restructuring is that it is usually done in the months when the tourism receipts in the form of Value Added Tax turnovers are usually accumulated by the Bulgarian the tax administration. The need of proper forecasts that could eventually justify or reject such a hidden harvesting policy has never been examined and put to the public attention. The present paper regards several major problems in the application of the exponential smoothing methods for the purpose of the long-run forecasting of the monthly volume of the tourism receipts in Bulgaria. These problems include: (i) the problem of determining the time series pattern; or the so-called forecast profile; (ii) the selection of a suitable forecasting method; (iii) Calculating of short-run and long-run forecasts; (iv) the comparison of the results of the forecast techniques on the basis of the errors in the forecasts. As a result the Holt-Winters method is applied with the conclusion that the produced forecasts could trigger a process a more financially autonomous national tourism administration that will allow a greater part of the collected tax revenues for the tourism sector to be returned into the tourism industry in a form of public investments through this very same more autonomous national tourism administration.
Keywords: Forecasting, exponential smoothing, Holt-Winters method, monthly tourism receipts.
RESUMO
Em conformidade com a Lei anual para o Orçamento do Estado, o Ministério búlgaro das Finanças faz geralmente, duas vezes por ano, uma reestruturação do orçamento interno nos orçamentos dos diversos ministérios e órgãos estaduais do Estado búlgaro. O que é intrigante nesta reestruturação interna do orçamento é que ela é feita geralmente nos meses em que as receitas do turismo na forma de volume de receitas do IVA são normalmente acumuladas pela administração fiscal búlgara. A necessidade de previsões adequadas que possam, eventualmente, justificar ou rejeitar tal política de coleta encapotada nunca foi examinada e colocada à atenção do público. O presente artigo aborda vários problemas substanciais na aplicação dos métodos de suavização exponencial para efeitos de previsão de longo prazo do volume mensal das receitas do turismo na Bulgária. Estes problemas incluem: (i) o problema da determinação do padrão de séries temporais; ou o chamado "perfil de previsão"; (ii) a seleção de um método adequado de previsão; (iii) o cálculo de curto prazo e as previsões de longo prazo; (iv) a comparação dos resultados das técnicas de previsão com base em erros nas previsões. Como resultado, o método de Holt-Winters é aplicado com a conclusão de que as previsões produzidas poderiam desencadear um processo de uma administração nacional de turismo financeiramente mais autónoma, o que permitiria que a maior parte das receitas fiscais cobradas no sector do turismo pudesse ser devolvida à indústria do turismo na forma de investimentos públicos através de uma administração nacional do turismo mais autónoma..
Palavras-chave: Previsão, suavização exponencial, método de Holt-Winters, receitas turísticas mensais.
1. Introduction
In Compliance with the annual Act for the State Budget, the Bulgarian Ministry of Finance usually makes twice a year the so called Internal compensating changes in the budget credits of the first rate holder of budget credits (Ministry of Finance, 2014). Behind this complex phrase is hidden a not very popular state account practice of restructuring (increasing or decreasing the separate budget categories) in the budgets of the separate Ministries and State Agencies of the Bulgarian State. What is in intriguing in this internal budget restructuring is that it is usually done in the months of March and April in the first part of the year and then in the months of September and October for the second half of the year, when the tourism receipts in the form of Value Added Tax turnovers are usually accumulated by the National Revenue Agency (the tax administration) of Bulgaria. The need of proper forecasts that could eventually justify or reject such a hidden harvesting policy has never been examined and put to the public attention.
Furthermore, if revealed with the help of the proper forecasting techniques, this hidden policy of harvesting on the back of the Bulgarian tourism industry, could finally result in the creation of a more financially autonomous national tourism administration (preferably a Ministry of tourism) that will allow a greater part of the collected tax revenues for the tourism sector to be returned into the tourism industry in a form of public investments through this very same more autonomous national tourism administration.
Based on the monthly data available data in category Traveling of the balance of payment of the Republic of Bulgaria, which are regularly sustained and published by the Bulgarian National Bank on its web site (Bulgarian National Bank, 2014), a time series can be built for the volume of the tourism receipts (Graph 1) from January 2000 to March 2014. This time series comprises a set of 170 time periods (170 months).
Taking into the considerable size of this time series a search can be made for a suitable forecasting model for the monthly volume of Bulgarias tourism receipts. A possible solution in this regards could come in the face of the so-called univariate methods (DeLurgio, 1998) and namely and most particularly in the group of the exponential smoothing methods. This group of methods relies on the assumption that if a considerably long time series of a certain indicator can be composed, this very same considerably long time series will have reflected all the possible external influences induced by all the possible external factors and thus time series will have incurred an internal logic of development and an internal information signal could be extrapolated further in future. The building up of forecast model, especially with the use of the exponential smoothing methods, however, needs a more sophisticated and multistage approach with a certain number of clearly set objectives.
2. A literature review on the topic
The development and usage of the exponential forecasting methods dates back from the works of R. G. Brown in the 1940s the results of which were published in 1959. These were further developed and expanded by C. C. Holt in 1957 and Peter Winters in 1960.
In 1960s Pegles (1969) developed the first taxonomy for the classification of the available at that time exponential smoothing forecasting methods. In the 1980s Gardner (Gardner, 1985; 1987) presented some interesting techniques aimed at smoothing of the error residuals in the achieved forecasts. Gardner (1985) and Taylor (2003) also further expanded the opportunities for classifying the exponential smoothing forecasting methods according to so-called forecasting profiles or forecasting patterns (See also point 3).
The problem of the initialization of variables that are to be used in the exponential smoothing equations was also regarded by a numerous authors such as Ledolter and Abraham (1984) and Hyndman (2014). In 2002 Hyndman, Koehler, Snyder, Grose, and later in 2008 Hyndman, Koehler, Ord and Snyder published there works on the usage of the so-called state-space approach in exponential smoothing.
In the years, the capacity of the exponential forecasting methods to produce reliable forecast was further explored also by other researchers such Ledolter and Abraham (1984), Gardner and McKenzie (1985; 1988), Chatfield and Yar (1988), Hamilton (1994), Tashman and Kruk (1996), Delurgio (1998), Williams and Miller (1999), Tsay (2005) and many others.
In Bulgaria, the exponential smoothing methods up to the 1990s were virtually unknown due to the weak English language skills of the researchers and the preference given in the field of forecasting to the multivariate forecasting methods and mainly the usage of French and Swedish econometric models. In 1996 Sirakov published a book named Conjuncture and Forecasting of International Markets in which an application of the Browns single exponential smoothing was made in regards to the Bulgarian export of textile production equipment and machinery for the African countries and mainly in Nigeria. This application was however very narrow in scope. An Internet publication that that tried to make the exponential forecasting smoothing methods more popular in Bulgaria was made in 2007 by Ivanov form the New Bulgarian University as a part of his lecture course materials on business processes forecasting. Another try for a more explicit explanation and usage of the exponential forecasting methods and namely the Halt and Halt-Winters method was made in another book published in Bulgarian language by Mishev and Goev, i.e. Statistical analysis of time series (2012). Even here, however, the theoretical presentation of the regarded method was limited and narrowed to the practical application of several software packages. In the field of the Bulgarian tourism, the publish studies in the application of the exponential smoothing methods are also limited to some few papers dealing with the application of the Halt and Halt-Winters method for forecasting of the number of tourism arrivals in certain areas and in the country as a whole.
3. Objectives
The task of creating an exponential smoothing forecast model for the monthly volume of the Bulgarian tourism receipts, meets with solving of several major problems:
- Determining the time series pattern, or the so-called forecast profile (Gardner, 1987, pp.174-175) (Hyndman, Koehler, Ord & Snyder, 2008, pp.11-23) and the quality of the data in the pattern, on the basis of which to select the suitable forecasting exponential smoothing model.
- Selecting of a suitable forecasting techniques;
- Calculating the forecast values (up to March, 2025) and finding of a best-fit model on the basis of the errors in the forecasts (R2, Mean Absolute Percentage of Error (MAPE) and etc.);
- Drawing of conclusions on the results of the achieved forecasts.
4. Methodology and main results
With regards to the first problem, set in the previous point of the present paper, i.e. the problem of determining the times series pattern, or the so-called times series forecast profile is usually solved by comparing the times series in regard with a pre-set classification of exponential smoothing methods or the derived form them forecast profiles in terms of development curves (Dimitrov, 2011) (Dimitrov, 2013). As Hyndman et al. (2008, pp.11-12), this classification of smoothing methods originated with Pegles taxonomy (Pegles, 1969, pp.311-315).
A simple visual analysis of the times series of the monthly volume of the tourism receipts in Bulgaria for the time period 1964 – 2012 with Hyndman et al and Taylors classification (Table 1) shows out that these particular time series can be associated to the following group of forecasting patterns (forecasting profiles according to the Garnders classification) called the linear trend, multiplicative seasonality profile (A,M pattern) and (iii) to the liner trend, additive seasonality profile (A,A pattern) (Graph 2).
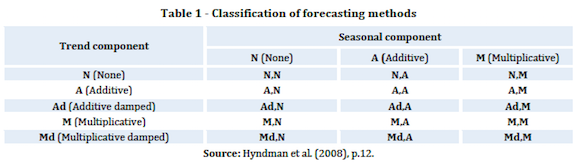
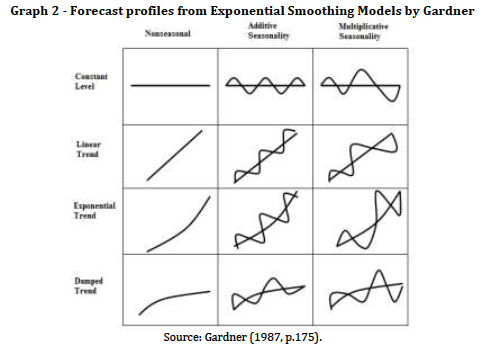
A more detailed visual review of the regarded times series on the basis of the fluctuations maxima and minima shows out that there are clearly expressed yearly cycles, i.e. cycles of 12 months with an increasing amplitude in the cyclical fluctuations. This finding can be further used in the process of selecting the proper forecasting technique.
The finding that the time series of the monthly volume of the tourism receipts in Bulgaria for the time period January 01, 2000 – March 31, 2014 have clearly expressed in terms of increasing fluctuations cycles, as well as the fact that it corresponds to the linear trend, multiplicative seasonality profile (A, M pattern), provides a solution to the third problem, the one of selecting and using of a suitable forecasting exponential smoothing method. As both Gardner and Hyndman et al. point out this profile corresponds to the method of the triple exponential smoothing in the presence of a linear trend and multiplicative seasonality, known also as a variation of the Holt-Winters method. The mathematical notation of the Holt-Winters method for multiplicative seasonality is as follows:
The smoothing of the level (the base) – “B”:
![]()
The smoothing of the trend – “Т”:
![]()
The smoothing of the seasonal factor – “S”:
![]()
The achieving of the final forecast “Ft+m” for “t+m” periods ahead in the future:
![]()
Where: „α”, „β” and “γ” are the smoothing constants for the level, the trend and the seasonality respectfully which could take values between 0 and 1.
The initialization of the values of the level “B”, the trend “Т” and the seasonal factor “S” is achieved though the following set of equations:
For the level (the base) – “B0”:
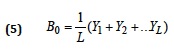
For the trend – “Т0”:
![]()
For the seasonal factor – “S0”:
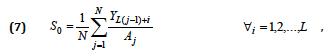
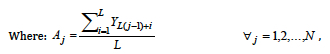
and Aj is the average value of Y in the jth cycle of the regarded time series.
Here, for the initialization of the seasonal factor other alternative methods are also available and R. J. Hyndman (2014) recommends the following approach for the multiplicative seasonality:
![]()
However the present paper will use equation (7) even if it is a little bit more complex to achieve and is close to an autoregressive approach for initialization of the seasonal indices.
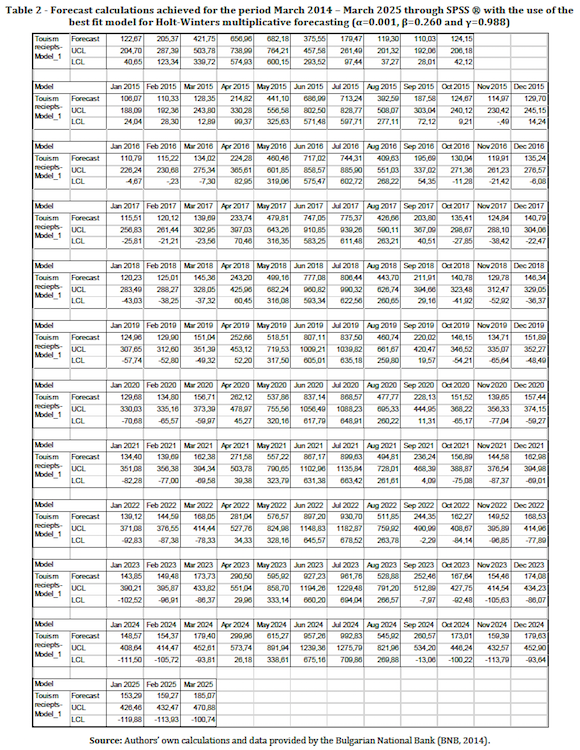
After having chosen the Holt-Winters method for multiplicative seasonality as the proper forecasting technique, a calculation of the forecasts up to March, 2025 and finding of the best fit model can be made (the third of the above-set tasks). In order make the necessary forecast calculations and to receive the optimal values of the smoothing constants in regards to R2, Mean Absolute Percentage of Error (MAPE) and etc., one can use the inherent functions of various statistical software packages such as R, R Studio, NumXL ®, SPSS ® and many others. The present paper shall use the function of the SPSS ® statistical software for producing of the necessary forecast calculations by the use of the Holt-Winters exponential smoothing method. The same software package shall be used simultaneously for finding of the best fit exponential model smoothing parameters, i.e. the-best fit the alpha, beta and gamma smoothing constants (Graph 3). The forecasting results of the best fit model achieved through the SPSS ® software package are presented in Graphs 3 and 4 and in Table 2. The set of the smoothing constants produced for the model are α=0.001, β=0.260 and γ=0.988.
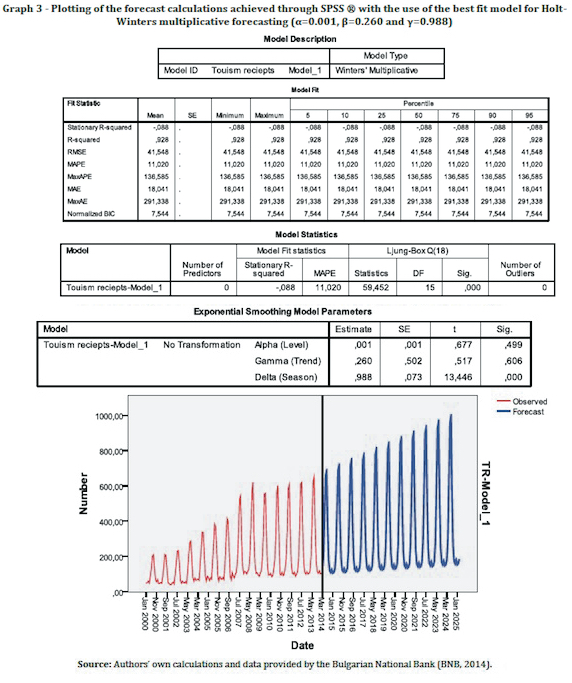
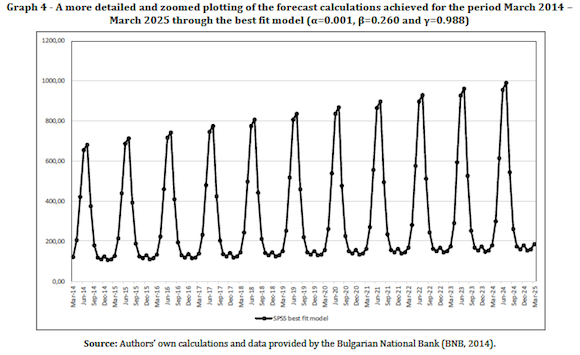
After producing the optimal forecast calculations through the best fit model (the one with lowest MAPE) one can proceed further with the solving of the fourth of the above set tasks, i.e. with the drawing of conclusions on the results of the achieved forecasts.
5. Conclusions
Based on the results in Table 2, as well as in Graph 3 and 4, one can outline that the forecasts achieved with best-fit model is that the trend of increase is preserved. Moreover, the best fit model achieved through the SPSS statistical package with smoothing constants α=0.001, β=0.260 and γ=0.988 tends to produce, as it should be expected, multiplicatively increasing cyclical fluctuations for the monthly volume of the tourism receipts in Bulgaria. The highest forecast monthly values, as well as the statistically recorded ones, however, do not refer to the months of March and April and September and October, when the internal compensating changes in the state budget are being made by the Bulgarian Ministry of Finance. The highest forecast values for the winter season are produced for the months of November and December and for the summer season, respectfully for the months of June and July. The lack of overlapping can be easily explain with the lag of one to two months that is needed for the tourism receipts in Bulgaria to produce the necessary Value Added Tax turnovers in the tourism companies which can be consequently captured as tax revenues by the National Revenue Agency (a branch agency of the Bulgarian Ministry of Finance). This means that, intentionally or not that, if the Bulgarian state in the face of its Ministry of Finance continues the practice of the Internal compensating changes in the budget credits, based on both recorded data and produced forecast, the hidden policy of harvesting on the back of the Bulgarian tourism industry will also continue. And there will not be any public notion about it as it will be covered up as a routine bureaucratic state accounting procedure that is either too complex or too routine and insignificant to explain.
This policy of hidden harvesting, however, has an explicit downturn effect on the development of the Bulgarian tourism and prevents the increase in its competitiveness (Filipova, 2010) (Dimitrova, 2013) (Stankova, 2010; 2014) (Gantchev, 2014). And the main reason for this is the fact that the Bulgarian national tourism administration for the last 25 years has always been either a part of a certain mega ministry (like the former Ministry of Economy, Energy and tourism) has possessed a rank of Government agency but without any power of being directly presented in the government with the right to coordinate the preparation and adoption of the state budget and to spend directly its budget without a prior approval from a supervising minister from a ministry which incorporates it. In more simple words this long lasting situation has contributed either for an ever decreasing, or for an insufficient return of the collected taxes in the tourism industry in the form of public investments.
The fact that the forecasts for monthly volume of the tourism receipts in Bulgaria point a continuous increase in both the fluctuations and their yearly volume by March 2025 should result in a greater pressure form the Bulgarian tourism industry (mainly from the different sub-sectorial associations) on the political parties and the government for the creation of a more financially autonomous and more vivid national tourism administration than the existing one.
References
Brown, R. G. (1959). Statistical Forecasting for Inventory Control. New York: McGraw-Hill. [ Links ]
Chatfield, C. & Yar, M. (1988). Holt-Winters forecasting: Some practical issues. The Statistician, 37, 129-140. [ Links ]
DeLurgio, S. A. (1998). Forecasting Principles and Applications. Pennsylvania State University: Irwin/McGraw-Hill. [ Links ]
Bulgarian National Bank. (2014). Balance of Payments of Bulgaria, 2014. Retrieved May 29, 2014 from http://www.bnb.bg/ResearchAndPublications/PubPeriodical/PubStatisticalPublications/PubSPBalancePayments/index.htm. [ Links ]
Dimitrov, P. (2011). Long-Run Forecasting of Spa and Wellness Subsector of the Bulgarian Tourism Industry. Tourism & Management Studies, 7, 140-148. [ Links ]
Dimitrov, P. (2013). Long-Run Forecasting of the Number of Ecotourism Arrivals in the Municipality of Stambolovo, Bulgaria. Tourism & Management Studies, 9(1), 41-47. [ Links ]
Dimitrova, R. (2013). Opportunities of marketing research for increasing competitiveness of the cultural tourism product. [ Links ] Paper presented at the International Scientific Conference Cultural Corridor Via Diagonals – Cultural Tourism Without Boundaries, Sofia, Bulgaria.
Filipova M. (2010). Peculiarities of project planning in tourism. Perspectives of Innovations Economics and Business /PIEB, International Cross- Industry Research Journal, 4(1), 57-59. [ Links ]
Gantchev, G. T. (2014). Tourism Industry: Role of the real effective exchange rate. Tourism & Management Studies, 10(Special Issue), 174-179. [ Links ]
Gardner, E.S. & McKenzie, E. (1985). Forecasting trends in time series, Management Science, 31, 1237-1246. [ Links ]
Gardner, E.S. & McKenzie, E. (1988). Model identification in exponential smoothing, Journal of the Operational Research Society, 39, 863-867. [ Links ]
Gardner, E. S. (1985). Exponential Smoothing: the state of the art, Journal of Forecasting, 4, 1-28. [ Links ]
Gardner, E. S. (1987). Smoothing methods for short-term planning and control. In S. Makridakis & S. C. Wheelright (Eds.) The handbook of forecasting – a managers guide, (pp. 174-175). New York: John Wiley & Sons. [ Links ]
Hamilton, J .D. (1994). Time Series Analysis. Princeton, NJ: Princeton University Press.
Holt, C. C. (1957). Forecasting trends and seasonals by exponentially weighted averages, O.N.R. Memorandum 52/1957, Carnegie Institute of Technology. [ Links ]
Hyndman, R. J., Koelher, A. B., Ord, J. K., & Snyder, R. D. (2008). Forecasting with exponential Smoothing – The State Space Approach. Berlin: Springer. [ Links ]
Hyndman, R. J. (2014). Initializing the Holt-Winters method. In Hyndsight – A blog by R. J. Hyndman. Retrieved March 10, 2014 from http://robjhyndman.com/hyndsight/hw-initialization/. [ Links ]
Ivanov, M. (2007). A try and conclusions from the forecasting of the business processes with the help of time series (a MS PowerPoint presentation in Bulgarian language). Retrieved May 29, 2014 from: http://www.nbu.bg/PUBLIC/IMAGES/File/departments/informatics/Izsledvania/Martin_Ivanov_prolet_2007.pdf. [ Links ]
Ledolter, J. & Abraham, B. (1984). Some comments on the initialization of exponential smoothing. Journal of Forecasting, 3, 79-84. [ Links ]
Ministry of Finance (2014). Type of corrections which can be currently exercised in the fiscal year in the budgets of the first rate users of budget credits in compliance of the Act for the structure and functioning of the state budget (in Bulgarian language). Retrieved May 29, 2014 from http://www.minfin.bg. [ Links ]
Mishev, G. & Goev, V. (2012). Statistical Analysis of Time Series. Sofia, Bulgaria: Avangard-Prima Publishing House. [ Links ]
Pegles, C. C. (1969). Exponential forecasting: some new variations. Management Science, 15(5), 311-315. [ Links ]
Sirakov, S. (1996). Conjuncture and Forecasting of International Markets. Sofia, Bulgaria: Stoilov Publishing House. [ Links ]
Stankova, M. (2010). The tourism regions in Bulgaria - concepts and challenges. Journal of Tourism & Hospitality Management, 16(1), 109-118. [ Links ]
Stankova, M. (2014). Challenges ahead for Bulgarians competitiveness as a mountain tourism destination. Tourism & Management Studies, 10(Special Issue), 180-185 [ Links ]
Taylor, J. W. (2003). Exponential Smoothing with a damped multiplicative trend. International Journal of Forecasting, 19, 715-725. [ Links ]
Tashman, L. J., & Kruk, J. M. (1996). The use of protocols to select exponential smoothing procedures: a reconsideration of forecasting competitions. International Journal of Forecasting, 12, 235-253. [ Links ]
Tsay, R. S. (2005). Analysis of Financial Time Series. New York: John Wiley & Sons. [ Links ]
Williams, D. W., & Miller, D. (1999). Level-adjusted exponential smoothing for modeling planned discontinuities. International Journal of Forecasting, 15, 273-289. [ Links ]
Journal history:
Received: 12 May 2014
Accepted: 10 November 2014














