Introduction
Mathematical structuring and spatial structuring, in particular, have become increasingly prominent in mathematics education research due to their influence on mathematical understanding. Spatial structuring consists of the “mental act of constructing an organization or form for an object or set of objects” (Battista & Clements, 1996, p. 282) through the identification of its spatial components, the establishment of relationships between components into spatial composites, and between and among components and composites (Battista et al., 1998), for example by forming composites and relating them to each other and to the shape as a whole.
The research developed by Battista and Clements (1996), Battista et al. (1998), Cullen et al. (2018), Sarama and Clements (2009) and Outhred and Mitchelmore (2000), on the understanding of area and volume, show how spatial structuring influences the understanding of these concepts and how pupils progress in their learning. Other studies, such as that of van Nes and Lange (2007) and that of van Nes and van Eerde (2010) have highlighted, for example, the contribution of spatial structuring to the construction of number sense. These works show that the transition from an understanding based on isolated units (components) to the formation of composites is a progression towards a more sophisticated structure, based on the coordination of these components and composites. Coordination is a fundamental operation in spatial structuring and one which underlies this process, since it sheds light upon how the different parts are interrelated and how they relate to the shape as a whole. However, coordinating is a complex process which pupils frequently have difficulty in grasping, as described in the aforementioned studies. As these studies focus on spatial structuring in numerical and measurement contexts, it is important to extend the research to geometrical contexts.
More recent research focusing on spatial reasoning has led us to a consideration of its presence and importance in spatial structuring. Jones (2001) defines spatial reasoning (SR) as “the process of forming ideas through spatial relationships between objects. It is the form of mental activity which makes it possible to create spatial images and manipulate them in the course of solving practical and theoretical problems” (p. 55). This definition points to a close relationship between spatial structuring, as a form of abstraction of organization of an object, and spatial reasoning, as a process in which the images provided by spatial structuring are manipulated to solve problems. For example, composing and decomposing shapes are examples of spatial reasoning (Davis et al., 2015) that offer a fundamental contribution to the understanding of the structure of shapes where coordination has a crucial role. In the context of composing and decomposing three-dimensional shapes, Sarama and Clements (2009) propose a learning trajectory for the composition of three-dimensional shapes with unit blocks, in the early years, showing that even very young pupils are able to establish complex relationships. Therefore, it is necessary to better understand how first graders use these spatial reasoning processes to structure three-dimensional shapes, since it is also at around this age that they begin to construct increasingly abstract forms of representing reality.
Thus, the aim of this study is to gain further understanding of the strategies used by pupils to reproduce a 3D shape, from the perspective of spatial structuring, and the spatial reasoning processes involved in this reproduction. From this, two questions emerge: What strategies are used by pupils to reproduce 3D shapes from a 3D model and from a 2D representation of a 3D model? How do pupils coordinate components and composites and how do they relate them to the whole? What spatial reasoning processes are used by pupils?
To this end, we analysed the strategies used by three first graders in two tasks related to the reproduction of 3D shapes, the first from a 3D model and the second from a 2D representation of a 3D model.
Theoretical backgroung
In this section, we present and discuss the two central concepts in this paper: spatial structuring and spatial reasoning. In both concepts, we try to clarify their importance and contribute to the formation of mental models based on spatial relationships.
Spatial structuring
According to Battista (2008), spatial structuring consists of the act of mentally representing an object and the relationships present in the structure of that object, through an identification of the components, the establishment of relationships between components in composites and the establishment of relationships between components, composites and the whole. For example, in a 3D shape constructed with cubes, the cubes are understood as components, while the composites may be lines or columns or horizontal or vertical layers, but they may also be sets of cubes that are interrelated and also related to a part of that shape, like an L arrangement. The spatial structuring process leads to the creation of a mental model that represents that object, but which can generally be extended to the analysis and structuring of a broader set of objects with similar characteristics. Hence, Mulligan and Mitchelmore (2009) stress that it is crucial to progress from work based on loose parts to work with composites.
Spatial structuring is defined in a very similar manner by Sarama and Clements (2009), taken as a mental operation and a form of abstraction. The processes of selecting, coordinating, unifying, and memorizing an object or a set and the actions performed upon these objects enable pupils to abstract their structures. Although Sarama and Clements (2009) restrict the concept of spatial structuring to area and volume, the discussion of the last decade and a half around what structuring actually concerns (e.g. Mulligan & Mitchelmore, 2009; Venkat et al., 2019) in mathematics, suggests that the concept should be used in a broader sense. In fact, while spatial structuring is important in the context of measurement, it may also be important in the geometrical context and contribute to the understanding of shapes’ properties, as shown, for example, in the study of Battista (2008).
Mulligan and Mitchelmore (2009) and Mulligan et al. (2020) list a series of mathematical domains where spatial structuring is necessary for the understanding of their structures, and which imply iteration, grouping, partitioning and unitization processes. In their study, focusing on the understanding children aged 5 to 6 years have of mathematical patterns and structures, the authors propose five levels for structural development: pre-structural stage (representations do not show evidence of numerical or spatial structuring); emergent stage (representations highlight relevant features of a given structure); partial structural stage (representations show evidence of the most significant numerical or structural features); structural development (representations integrate numerical and spatial characteristics); and advanced structural stage (representations show an efficient and generalised use of the underlying structure).
As shown in this description, the structuring of shapes initially occurs at a local level and only later at a global level. According to the proposal of Battista and Clements (1996), local structuring is referred to when relationships are established between components and composites, but when their relationship with the whole is not yet evident. Global structuring is observed when the relationships established between components, composites and the whole coherently represent the structure of the shape, and these relationships may emerge with resort to concrete materials or based on a previous mental model. In the framework proposed by Mulligan and Mitchelmore (2009), local structuring appears to correspond to the second and third levels, while global structuring corresponds to the fourth and fifth.
In spatial structuring, there are two fundamental operations: coordination and integration. As mentioned by Cullen et al. (2018), pupils establish interrelationships between different parts of a shape through coordination, such as recognizing relationships between components or acknowledging that the same cube is part of two intersecting views. In order to coordinate two cube composites, pupils need to be able to recognize which of the cubes intersect both views so as not to double the number of cubes required. In the case of global structuring, coordination is always present, due to the type of relationships that are established. However, the support of concrete materials may be required, or it may operate solely at a mental level. The coordination operation may or may not be present at a local level. It will be absent if there is manipulation of unrelated components. It will be present if relationships are established between components or between composites.
The study of Battista and Clements (1998) highlights how the coordination of composites is particularly difficult for 3rd, 4th, and 5th graders, leading them to make counting errors when trying to determine the total number of cubes in each construction. The pupils in this study displayed difficulties in coordinating the views of the construction, as they duplicated the cubes at the intersection of two views. Other studies such as Mulligan and Mitchelmore (2009), van Nes and van Eerde (2010), and Sarama and Clements (2009) show that the ability to coordinate parts of a shape with each other and with the whole may be prior to this age, suggesting that this ability may be associated with learning experiences.
The integration operation is related to the construction of mental representations of the shapes that preserve their properties, incorporating the interrelationships between the different parts (Battista & Clements, 1996), which in turn implies use of the coordination operation. According to Battista and Clements (1996), the integration of different views of a 3D construction, to form one coherent mental model of it, may be accomplished through two alternative processes: by recalling similar objects that pupils already have perceived or conceived; or, in the event of no recalled object to be suitable for a model, by transforming existing mental images into new images that represent the object.
Pupils’ progression from local to global structuring appears to depend on their ability to coordinate components, composites and the whole (Battista & Clements, 1996), and to integrate mental models representing the structures of the shapes which allow for their mental manipulation. According to Casey et al. (2008), as children become more aware of spatiality, they are able to combine increasingly complex structures and thus show an increasing capacity for integration. This requires that children recognize parts and understand how they can be combined to form the whole (Casey et al., 2008). This means that pupils create progressively more sophisticated mental images, which also enable them to move from a construction by trial and error to a construction with anticipation, as mentioned in the 3D shapes’ learning trajectory for the composition proposed by Sarama and Clements (2009). Thus, Casey et al. (2008) claim that the ability to build more complex structures occurs simultaneously with the ability to mentally represent hierarchical spatial relationships.
Spatial reasoning
The definition of spatial reasoning by Jones’ (2001), presented in the Introduction, refers to the process of creating mental images and manipulating them to solve a given problem. This idea is also present in Battista’s definition (2007), where spatial reasoning is defined as “the ability to ‘see’, inspect and reflect on spatial objects, images, relationships and transformations” (p. 843). It includes processes such as creating images, analysing images to answer questions, and on operating images as well as storing these images to be recalled in other mental operations.
Although Battista defines spatial reasoning as an ability, Davis et al. (2015) appear to agree with Jones (2001), taking spatial reasoning as a set of processes organized in two “co-involved, complementary and inextricable” (p. 141) parts: ‘mental’ understanding and ‘physical’ transformations. The part related to understanding comprises processes such as: sensating, including visualizing and tactilising; interpreting, which includes comparing, symmetrising, and relating; and (de)constructing, such as composing and decomposing, organizing, and reorganizing. The part related to transforming covers processes such as moving, including sliding, rotating, reflecting, balancing; situating, which includes locating and guiding; and changing, focusing on dilating and contracting, distorting and morphing, and folding.
The definition, advanced by Davis et al. (2015), appears to add a relationship between what is mental and what is physical to the previous definitions, which is particularly important in the early years. Hence the claim by Bruce and Hawes (2015) that these processes are means to lead pupils to explore and investigate space as a basis for understanding more abstract representation models.
Spatial reasoning is understood as an ability that is realized through a broad range of processes that affect the spatial properties of an object. At an initial phase, these processes can be supported by concrete situations and manipulatives as a basis for creating mental representations.
Methodology
As part of a broader research project on spatial structuring processes (Conceição & Rodrigues, 2020), this paper focuses on spatial structuring strategies of 3D shapes, namely on how pupils coordinate the different parts of a shape, and on the use of spatial reasoning processes. It is a qualitative study with a design-based research (DBR) approach, geared towards creating a local learning theory focused on spatial structuring and relating it to the pedagogical resources that support this learning (Gravemeijer & Cobb, 2006). In this teaching experiment, this means that pupil’s progression on spatial structuring and the possibility of performing movements using manipulatives, in an initial phase, seem to be strongly related.
The teaching experiment
The teaching experiment included three task sequences and was implemented in twenty 60-minute sessions, between December 2018 and June 2019. Each class was planned to take three main stages into consideration: presentation of the task, autonomous peer or individual work, and a final whole-class discussion on student’s resolutions and strategies. A different task was proposed in each session, seeking to give the pupils the opportunity to explore the relationships in 2D and 3D shapes, as well as to explore the relationships between two-dimensional and three-dimensional representations.
The tasks analysed herein were the 14th (3D Reproduction from a 3D model) and 15th (3D Reproduction from a 2D representation of a 3D model) to be implemented, after the pupils had already had the opportunity to explore and discuss several 3D constructions.
Participants
The teaching experiment was implemented in a first-grade class of 24 students (6 and 7 years of age). Since it would not have been possible to analyse all 24 pupils’ strategies during the period allocated to this research, three students were selected for a more in-depth analysis, namely Raquel, Dalila and Gil (fictitious names). This selection was based on a previous observation where the pupils were able to describe their reasoning with relative ease, regardless of their performance in mathematics. The strategies presented by these pupils are representative of the strategies of the pupils in the class. The class teacher prepared the implementation of the tasks in partnership with the first author and was mostly responsible for implementing the tasks and managing the pupils’ work.
Methods and instruments
Participant observation with video recordings of the pupils’ autonomous work and the whole-class discussion was used. We sought to collect data on their productions and construction processes, namely by recording the shapes they built and the movements they performed to build those shapes. We also recorded their interventions in whole-class discussions, where the pupils explained and discussed their ideas with the teacher and their peers. These two sources of data provided a greater diversity of information that could be cross-referenced to better understand pupils’ ideas.
It should be acknowledged that access to the pupils’ ideas, with regard to spatial structuring and spatial reasoning, may be limited since these processes are primarily mental. In order to overcome this limitation, data triangulation was used, and the images collected by video recording (how the pupils manipulate the materials and the gestures they make) were cross-referenced with the pupils’ discourse, during autonomous and collective work.
Tasks
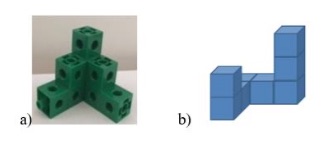
For a better understanding of the strategies used by the pupils to reproduce 3D shapes, we have selected two tasks as mentioned above: 3D reproduction from a 3D model and 3D reproduction from a 2D representation of a 3D model. In the first, the pupils were given a 3D model such as that shown in a) Figure 1 and were asked to construct a replica with loose cubes. The pupils were allowed to observe the model and rotate it but could not disassemble it. In the latter, the pupils were given a two-dimensional representation of a 3D model(b), Figure 1) on a sheet of paper to construct the corresponding three-dimensional shape, using multilink cubes. The sequence by which the tasks were proposed to the students was intentional since it is more challenging to reproduce a 3D model from its 2D representation. Here we aimed to present two different types of tasks concerning the source given to reproduce. Since they were first graders, both tasks were proposed orally.
The reproduction of shapes implies that pupils mentally decompose the shape into components or composites for swifter and more efficient counting (van Nes & van Eerde, 2010), and that they physically coordinate these components and composites to form a new congruent shape. According to van Nes and van Eerde (2010), pupils develop more rapid counting processes through spatial structuring by grouping together components and by establishing relationships among them. In addition to these spatial structuring features, the selected tasks foster the operationalization of the processes associated with spatial reasoning, such as decomposing and composing or dimension shifting.
The shapes used in these tasks present the challenge of coordinating perspectives, implying the coordination of composites whose absence may lead pupils to duplicate or omit cubes. In the case of Figure 1b), it presents the additional and perhaps most relevant challenge of a shift from two-dimensionality to three-dimensionality. The fact that construction 1a) is symmetrical may be a facilitating feature and in construction 1b), the difference in the height of the vertical columns may serve as a guide for pupils. Although this is a process of construction with concrete materials, many of the processes occur in the concrete and abstract interaction.
Data analysis
The analysis framework began to emerge from the work of Battista and Clements (1996) and the work of Sarama and Clements (2009). The analysis framework we propose in Table 1 is a learning progression in terms of how pupils progress in spatial structuring. First, the type of relationships established were organized according to the proposal of Battista and Clements (1996), establishing two main levels: local structuring and global structuring. As the data were analysed and the responses were coded according to these two types of structuring, the presence of a pre-structural stage, as described by Mulligan and Mitchelmore (2009), was brought to light. This stage may be described as a global apprehension which had already been identified by van Hiele (1986) related to geometrical reasoning, and may also be found, albeit implicitly, in the work of Battista and Clements (1996) and Cullen et al. (2018). Throughout the tasks, data analysis corroborated the presence of these three levels, however some discrepancies were noted in the pupils’ responses. This led to each level being divided into the following sub-levels, presented hierarchically, for local structuring: Recognizing components (LS1); Establishing relationships between components (LS2); and Establishing relationships between composites (LS3). In the case of global structuring, the hierarchical sub-levels are as follows: Establishing relationships between components, composites and the whole by coordination (GS4); and Establishing relationships between components, composites and the whole by integration (GS5), considering here the difference between coordination, which may or may not operate at the mental level, and integration, which operates solely at the mental level. The analysed data were then categorized according to these levels. In the case of sub-levels 2 and 3, the strategies emerging from the study also made it possible to hierarchize new sub-levels in each of them.
Data were coded by letters and number(s). The letters make it possible to indicate the level of spatial structuring: PS for the pre-structuring level; LS, for the level of local structuring; and GS for the level of global structuring. The number(s) indicate(s) the sub-level (or sub-levels) of spatial structuring. The hierarchy established between these levels is relatively permeable as pupils may perform differently in the various tasks and progress significantly between levels in the same task.
The reference to construction by trial and error or by anticipation by Sarama and Clements (2009) is important to complete our framework. For a better understanding of the processes associated with the sub-levels, the features that emerged inductively from the data analysis itself and referred to as indicators were included. Therefore, the features considered in the analysis framework are inferences made based on our observation and videorecords of pupils’ work, discourse and movements they made while constructing. These indicators have been progressively refined.
Although this framework focuses on spatial structuring, these tasks have the potential to mobilize spatial reasoning processes that are supported by spatial structuring itself. The pupils decompose and compose, compare, relate, establish symmetrical relationships, locate, shift dimensions and rotate, among other processes.
Table 1: Analysis framework for spatial structuring levels
Results
In this section, we describe the strategies that pupils used to solve both tasks and relate them with our analytical framework and with the literature. We start with the results from the task where pupils were asked to reproduce the shape from a 3D model and after from a 2D representation of a 3D model. In each subsection, a different type of strategy is presented and discussed, and the processes associated with that strategy are taken into consideration.
Task: 3D building from a 3D model
Here, we analyse the strategies used by Raquel, Dalila, and Gil to reproduce a 3D shape from a 3D model. The following results not only show evidence of how students assemble the shape, but how they progress in the relationships that allow them to build the shape.
Construction from the extremity and emergence of composites
Raquel begins by looking at the model and taking a small amount of cubes from the box, looking back at the model to check the number of cubes. In Figure 2, Raquel may be observed initiating the construction at one of the extremities, progressing in a ladder-like construction until reaching the centre. When she completes this part, she rotates the direction of the construction 90o and continues in a downward motion towards the other extremity. At this initial phase, her construction strategy appears to be based on the recognition of relationships between the components, in which each adjacent column has one more cube than the previous one (LS2.1).
In this strategy, Raquel appears to follow a path associated with a ladder as she builds each column with one more cube than the previous column and understands at which point she needs to change the direction of the construction to then begin the descending path.
During the whole-class discussion, when Raquel explains her thought process, she presents a different strategy based on three composites: the central column, the L-shaped composite on the right, and another similar composite on the left, which she is unable to finish, as seen in Figure 3.
Raquel - I did this one first (showing the composite of 3 cubes on the right). Then this one (central column that connects to the first composite). And then I did that one in the same way as the other one (composite of 3 cubes on the left).
In this strategy, Raquel indicates three composites (referring to them as “this”) which she connects afterwards to assemble the shape according to the model (LS2.3).
Raquel does not complete the construction of the third composite, as may be seen in Figure 3, perhaps by doubting how to do it in a way that shows what she is seeing with her mind. She disassembles the entire construction and begins to construct again, using a different path, as shown in Figure 4.

Figure 4: Construction from the boundaries: strategy presented by Raquel in the whole-class discussion.
This time, Raquel constructs the boundaries of the shape, finishing by positioning the two cubes to form the ladder. She then decomposes the construction into the three aforementioned composites (“I did this one first, then this one, and then I did that one in the same way as the other one”) and uses them to finish the explanation (Figure 5). Her action of decomposing the construction into three composites and making this reference in her explanation suggests that Raquel is able to recognize these composites and had intended to use them in the first part of the strategy, although she had not managed to do so.
The pupil concludes her explanation when she shows the three separate composites she had intended to show at the beginning, stating:
Raquel - Then I did the other one in the same way (decomposing the shape into three composites and showing them to the class).
Raquel’s statement also appears to suggest the recognition of symmetry between the two parts of the construction, since she considers both composites equal, although they are in an inverted position (GS4).
Although Raquel did not appear to have anticipated these composites and the relationship between them at the beginning of the task, throughout its exploration, her actions and discourse suggest that she is becoming aware of the structuring of the construction in three composites as she begins her intervention in the discussion with an explicit reference to these composites. The manipulation of the cubes and the relationships she began to establish during this manipulation, namely the symmetry between the two parts of the construction, may have contributed to Raquel’s creation of a more consistent form of mental organization for that construction. Throughout her presentation, Raquel appears to always bear in mind the form of organization she presents, that is visible in Figure 5.
Thus, Raquel seemingly begins to explore the task with local structuring, by relating the components (LS2.1). However, the relationships she establishes from the sensory experience of manipulation of the cubes lead her to progress to a level that points to the establishment of relationships between composites (recognizing the congruence between two of them) and between composites and the whole (GS4).
Construction with rotation of a composite
Figure 6 highlights the strategy adopted by Dalila, based on a back-view observation of the model. This pupil begins by forming a column corresponding to the central part of the shape, then constructing each side, in a symmetrical linear arrangement. This approach to construction appears to suggest that the pupil does not immediately recognize a way to coordinate the cubes to form the right angle and, perhaps for this reason, she chooses to organize the construction in a straight line (LS3), by observing the construction from behind, at the suggestion of her peer next to her.
After placing all the cubes, Dalila observes the construction from the front and rotates, in a quarter of a turn, a part of the construction towards the centre, making the two parts of the construction form a right angle. With this rotational movement, which seemingly stems from anticipation of the result of such movement, the pupil completes the construction, thereby finding a way to coordinate the two vertical composites. Thus, and assuming, at the end of the construction, that it is the same as the model, Dalila appears to establish a relationship between these composites and the whole (GS4).
During the whole-class discussion, Dalila presents an explanation that shows that she did, in fact, have doubts when coordinating the two composites, as may be ascertained in the following excerpt:
Dalila - I had a doubt which was: I had put this one first, then this one, then this one (pointing in sequence the column of 3 cubes, the column of 2 cubes and the column of 1 cube). Then we moved to the other side, I had put this one here (column of 3 cubes) and realized that from the side, it wasn’t the same from the side because it wasn’t here (pointing to the column of 3 cubes). And then I tried to do it here (pointing to the columns of 2 cubes and 1 cube of the second composite) and I was able to make the shape.
Dalila’s explanation shows that she had doubts in the coordination of the two composites when she realizes that the second composite would not be the same as the one she had already constructed, as there is a part of the construction that is common to both composites. The progression in Dalila’s spatial structuring appears to occur when she finds discrepancies between her construction, which is based on a mental decomposition of the model, and the actual model. The pupil tries to find a construction form that is more consistent with the model, thus refining her initial idea. Her reflection seemingly contributes to the realization that the central composite intersects the two composites of the construction, thus allowing her to coordinate the two parts.
The construction process she presents in the whole-class discussion has a more static dimension than the process used in her autonomous work, however it is this dynamic process that appears to have brought the relationships to light for a more robust structuring of the shape.
Construction by layering
Figure 7 presents the path taken by Gil in his reproduction of the construction. The pupil begins by constructing the first layer, placing two cubes that only touch each other at one edge, and he appears to identify an angle formed by the two parts of the construction. He then places a cube in the corner, forming the right angle with the two previous cubes. Finally, he places the two cubes at the extremities. He then moves on to the construction of the second layer, using the same process. He places the top cube at the end.
The pupil begins by constructing the first layer, placing two cubes that only touch each other at one edge, and he appears to identify an angle formed by the two parts of the construction. He then places a cube in the corner, forming the right angle with the two previous cubes. Finally, he places the two cubes at the extremities. He then moves on to the construction of the second layer, using the same process. He places the top cube at the end.
The way Gil mentally decomposes the shape and then reconstructs it appears to result from a different kind of spatial structuring to that of his peers. While, in the previous cases, the pupils structured the construction into vertical composites, Gil coordinates horizontal layers, appearing to relate the arrangement of the layers to the whole by integration. Throughout this process, Gil seems to have a mental model in mind that allows him to anticipate aspects of his construction (GS5), thus showing evidence of global structuring of the construction.
Task: 3D building from a 2D representation of a 3D model
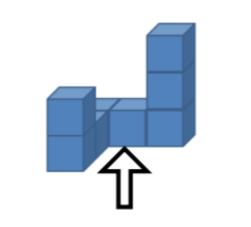
The following data refer to the second task, which involved the 3D reproduction of a 2D representation of a 3D model from the perspective illustrated in Figure 8.
Construction with composites, by vertical planes
Let us consider the strategy adopted by Raquel, who begins her construction horizontally from the most distant plane (back) to construct vertically to a closer plane (front), and ending with the construction of the column located on the right. The pupil uses mostly composites, in line with the sequence shown in Figure 9: first, a composite of two cubes (A) arranged horizontally in the back plane; then one cube (B) in front of the first composite; then, a composite of two cubes (C) arranged vertically, linking up this last cube; finally, she places a composite of three cubes (D), arranged vertically on the right.
The pupil appears to correctly identify the “in front of” and “on the right” relationships but seems to have some difficulty in coordinating the three vertical planes represented in the 2D representation. Raquel, therefore, places a cube in front of the initial horizontal composite, but assembles the vertical composite of two cubes on top of this cube instead of in front of it.
After constructing the shape, she disassembles it, possibly since she perceives it as being different to the 2D representation and begins to construct it again with the same configuration.
The researcher, and first author, approaches Raquel and challenges her to compare her construction with the image. Raquel observes the construction and quickly removes a cube from the leftmost column (Figure 10).
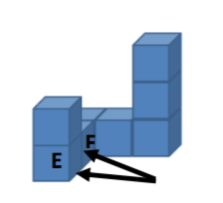
Seeking to lead the pupil to analyse the construction in more depth, the researcher asks Raquel to locate the parts that make up the shape in the 2D representation (Figure 11). Raquel rotates the construction and begins to point, with two fingers, at the composite she used initially, relating it to its location in the model.
She then associates the bottom cube (Figure 12) of the column of two cubes with the cube that is between the corner and this column (Figure 12 identified with F) but realizes that she has omitted a cube.
She reformulates the construction, placing the missing cube between the corner of the construction and the column of two cubes (Figure 13).
She then correctly relates the column of three cubes which is situated further to the right, holding the entire composite at the same time (Figure 14).
Thus, Raquel appears to be able to relate the 3D construction to the 2D representation, although she has revealed some difficulty in coordinating the different vertical planes, by fixing the composite of two cubes on top of the cube instead of to the front.
Raquel’s structuring of the shape appears, therefore, to be local since, although she works with the composites, they do not always relate to each other coherently (LS3). Raquel was also observed to identify inconsistencies between the model and the 3D construction and to correct them appropriately, despite only doing so when challenged to look in more detail, which may indicate that the relationships she establishes are not yet consistent.
Linear construction by front to back cube coordination
In the case of Gil, the pupil reproduces the shape by fluidly constructing cube by cube. He follows a linear path that goes from left (column A - Figure 15) to right (column B - Figure 15), as in the direction of writing, and from a closer vertical plane (in front) to a more distant plane (back). He appears to choose a different colour for the last composite, as may be seen in Figure 15. Throughout this process, Gil frequently rotates his construction in order to better fit the pieces, but always seems to bear in mind the plane of the construction.
It is not clear whether Gil already has a mental image of the construction or whether he creates one as he builds the shape and establishes new relationships. Nevertheless, the pupil shows evidence of being able to interpret the information in the 2D representation and transpose the relationships he finds there to the 3D construction, coordinating the different parts of the construction with each other and with the whole (GS4).
Linear construction by front to back composite coordination
In the case of Dalila, the pupil begins to construct her shape and, as she constructs, she explains her strategy to her peer Maria, who is alongside her:
Dalila - So, we do this: we start to do 2 (connecting two cubes, column A) (…) Then another two (connecting a second composite of two cubes horizontally, B, to the column she had already constructed, forming a right angle) (Figure 16), two plus two.

Figure 16: Linear construction by front to back composite coordination, by Dalila (initial composites).
Dalila repeats her explanation to Maria, while simultaneously pointing out each of the composites in the construction.
Dalila - Two (A) plus two (B) and then the one (C) (then connecting a cube to the composites she had already constructed, forming another horizontal right angle) (Figure 17).

Figure 17: Linear construction by front to back composite coordination, by Dalila (initial composites and component).
Maria - Tell me… Dalila - We put two, two, one. Three (connecting the three cubes that are left to form the second column, D) (Figure 18).

Figure 18: Linear construction by front to back composite coordination, of Dalila (assembling the final composite).
The pupil appears to mentally decompose the 2D model into composites of two or three cubes and associate them with parts of the 3D shape, respecting the relative position between the composites in their relationship with the whole (GS4). Dalila is thus able to interpret the 2D representation and, consequently, reproduce the 3D shape, appearing to have followed a strategy of front-to-back and left-to-right linearity, beginning with the leftmost column (A, Figure 17) and moving to the highest column (D. Figure 18).
Discussion
The strategies used by the pupils in both tasks are associated with different levels of spatial structuring in their local and global structuring. The pupils recognize the cube as a construction unit (component) and appear to establish relationships between the cubes with gradual complexity, as was the case of Raquel and Dalila in both tasks. The establishment of relationships between components, composites and the whole is very common. Although, in some cases, no initial anticipation is noted, such as, for example, in Raquel’s initial strategy in the first task, the strategies based on manipulation of the components give rise to the establishment of relationships which, in turn, lead to the formation of composites, based on more complex relationships, as mentioned by Casey et al. (2008) and Mulligan and Mitchelmore (2009). The results appear to indicate that in the case of Raquel and Dalila in the first task, the initial structuring corresponded to local structuring, which was refined during the task, progressing to global structuring. This progression implies the use of increasingly sophisticated mental images (Casey et al., 2008) that arise from the use of manipulatives and the reflection made during the manipulation (Battista & Clements, 1996). These pupils began by establishing local relationships, at the level of the components, to then form interrelated composites, while taking the relationship with the whole into consideration. However, in the second task, both Raquel and Dalila mostly use composites to reproduce the shape, which may be an indicator of how they structured the shape. Dalila even associates a number with each composite to refer to the amount of cubes it contains. The process of decomposing the 2D shape into composites appears to help them in the construction of the 3D shape.
In terms of spatial structuring, the presence of planes appears to be relevant. Some pupils structure the shapes in horizontal planes, as observed with Gil in the first task, when he constructs the shape in layers. In other cases, the planes appear to be vertical, as with Raquel, in the second task. In this case, the pupil appeared to have some difficulty in coordinating the components and composites according to these planes. In other situations, constructions following a linear path were observed, where the pupils began at one extremity of the shape and ended at the other as in the cases of Gil and Dalila, in the second task.
In both tasks, the pupils were seen to coordinate the components to form composites and, in most cases, they related these composites to each other appropriately. Although the first task could lead the pupils to duplicate the cubes of the central composite, a common difficulty described by Battista and Clements (1996), this did not occur, which shows their ability to coordinate these composites. In this task, coordinating the composites to form a right angle was challenging, particularly for Dalila who, through manipulation of the materials and, possibly, as a result of her own reflection on the comparison of the two constructions, rotated one of the composites, forming a shape that was coherent with the model. In the second task, the pupils also proved they were able to coordinate the composites to form different right angles in the shape, from their interpretation of a 2D representation. Even though coordinating composites is demanding for young pupils, in the cases described above, they seemed to be able to properly coordinate them with increasing sophistication, moving from an emergent stage, in some cases, to structural development, as proposed by Mulligan and Mitchelmore (2009) and Mulligan et al. (2020). This leads us to assume, on the one hand, the importance of manipulatives, to develop more sophisticated mental models of spatial structuring and processes of spatial reasoning, from the interaction between physical and mental manipulation, as mentioned by Davis et al. (2015).
In terms of spatial reasoning processes, the tasks presented in this study imply pupils’ use of (mental) decomposition and (physical) composition, two of the spatial reasoning processes of those enumerated by Davis et al. (2015). To construct the shapes, the pupils resorted to the process of locating components and composites and relating them to other components or composites. These three reasoning processes are common to all the resolutions presented herein, and made particularly evident by Raquel, when she pointed her fingers at two of the cubes that were part of the shape of the second task when relating them to the 2D representation.
In the first task, the fact that the shape was symmetrical may have made it easier for the pupils to make use of this relationship. For example, Raquel used the process of symmetrising for her construction, providing further evidence for this relationship in her explanation. In the case of Dalila, the pupil constructed the shape by placing it in a line, respecting this symmetry. Then, appearing to anticipate that when rotating one of the composites the shape would be coherent with the model, she performed this movement. This process appears to facilitate the visualization of the parts of the shape, allowing the pupils to relate these parts to each other and to the whole, contributing to a more in-depth understanding. In addition to the aforementioned processes, the second task implies another spatial reasoning process, namely dimension shifting, which was mobilized by all the pupils. In the second task, the three pupils alternate between the 2D representation and the 3D shape, seemingly bearing the construction path in mind.
These reasoning processes appear to support spatial structuring in the establishment of spatial relationships and, as mentioned by Jones (2001), in the creation of new mental images (Battista, 2007). Thus, spatial reasoning and spatial structuring may, in fact, influence each other. This appears to stem from both the formation of new and more sophisticated mental images, resulting from using manipulatives and refining mental images, and the increasing complexity of the reasoning processes. In this age group, manipulable materials are of fundamental importance in these processes.
Conclusions
In terms of strategies, the reproduction of the shapes implied the pupils’ mental decomposition of the models into components or composites which they then related to each other to physically compose the shapes. The relationships established may not have been anticipated, initially, but became increasingly complex supported by the use of manipulatives. In this interaction between the construction with materials and the comparison with the model, new, and progressively more sophisticated mental images appear to have been created, brought to light by the formation of composites and by the establishment of more complex relationships.
These relationships, that emerge from the interaction between physical and mental, also appear to have been supported by different spatial reasoning processes enumerated by Davis et al. (2015), such as symmetrising, rotating a composite, decomposing into horizontal layers, and dimension shifting. In some cases, the forms of decomposing and composing appear to be associated with local structuring, as, for example, when the pupils worked with components or composites and related them to each other, without, however, relating them to the whole. It was mainly in this type of structuring that the pupils used strategies such as the symmetrical linear arrangement, without yet coordinating the composites. In other cases, decomposing and composing were seemingly associated with the shape’s global structuring, emerging from the coordination of composites in their relationship with the whole or from the integration of a previous mental model, as in the case of the layered construction strategy.
Spatial structuring appears to have a close relationship with spatial reasoning, to the extent that, as a form of abstraction, it enables the creation of mental images that are necessary in spatial reasoning. At the same time, spatial structuring is apparently supported by the processes present in spatial reasoning and referred by Battista (2007) and Jones (2001), such as analysing objects (to understand), reflecting on them, manipulating them (transforming them) and establishing relationships, which contribute to the formation of these mental images. Thus, the processes associated with spatial reasoning seemingly resort to relationships that are present in the structure of objects, using them to generate new information while simultaneously providing further understanding of the structures of these objects.
It should be acknowledged that it is difficult to access pupils’ mental actions and, therefore, this is a limitation in this study. While using different sources to enrich the descriptions of the pupils’ work, the limited vocabulary and ambiguity of the meaning in the explanations are also limitations that should be taken into account. Considering the time limitations for an in-depth analysis of a larger sample, the small size of the sample and the fact that we analyse only two tasks should be taken in consideration. Thus, future research cycles with the same characteristics would be important.
This paper brings additional information to what is known on how pupils decompose and compose three-dimensional shapes from the work of Sarama and Clements (2009). Thus, these results show that work focusing on spatial structuring is possible and useful with pupils as young as those in the first grade of primary school. In addition, spatial structuring mobilizes progressively more complex spatial reasoning processes at the level of 3D shapes. Reciprocally, these processes also support progression in spatial structuring, showing the interrelationship between spatial structuring and spatial reasoning.