Introdução

Na legislação brasileira diferentes leis e decretos foram definidos ao longo das últimas décadas, considerando os direitos humanos, acessibilidade e, em especial, a inclusão de pessoas com deficiência nas instituições regulares de ensino. Dentre elas, destaca-se a Lei Brasileira de Inclusão da Pessoa com Deficiência - Lei n°. 13.146/15 (^{Brasil, 2015}), sancionada em 2015, que garante às pessoas com deficiência uma série de direitos essenciais à cidadania.

Dados do INEP/EDUCACENSO (^{Brasil/INEP, 2022}) apontam que, no ano de 2021, as instituições de ensino da rede pública e privada contemplaram mais de 1.350.000 matrículas de estudantes com deficiência, transtornos globais do desenvolvimento e/ou altas habilidades/superdotação na Educação Básica (de 4 aos 18 anos), abrangendo a Educação Infantil, Ensino Fundamental, Ensino Médio, Ensino Profissionalizante e Educação de Jovens e Adultos. Destas matrículas, 1.194.844 foram efetivadas em escolas regulares inclusivas e 156.077 em instituições de Educação Especial.

Neste artigo, apresenta-se um recorte de uma dissertação de mestrado, no âmbito do Programa de Pós-Graduação em Ensino Ciências e Matemática (PPGECIM), da Universidade Luterana do Brasil (ULBRA), com o objetivo de implementar¹ uma sequência didática para o desenvolvimento dos Campos Conceituais das estruturas aditivas e multiplicativas nos Números Naturais para um estudante cego congênito, sobre os conhecimentos matemáticos que são necessários para a autonomia de um estudante cego, de 11 anos, em processo de desenvolvimento do campo conceitual aditivo e multiplicativo, segundo a perspectiva de ^{Vergnaud (1998}). Contempla-se, também, exemplos de atividades importantes para o desenvolvimento dos campos conceituais aditivo e multiplicativo no conjunto dos Números Naturais, com a realização de intervenções pedagógicas ao longo dos anos de 2021 e 2022.

Reflexões sobre a Educação Matemática Inclusiva

No cenário escolar brasileiro, a Base Nacional Comum Curricular - BNCC (^{Brasil, 2018}), constitui-se em uma referência nacional para a elaboração de currículos buscando a diversidade cultural, a equidade e o respeito às diferenças, contemplando a Educação na perspectiva inclusiva. As premissas da Educação Inclusiva brasileira e da BNCC fundamentam-se no princípio da igualdade e no exercício de direitos e deveres do cidadão. Para tanto, o exercício da cidadania implica na participação efetiva da Pessoa com Deficiência nos diversos segmentos da sociedade.

Conhecimentos das linguagens, da Matemática e conhecimentos científicos como meios de expressão, de troca de experiências, que produzam significados, são indicados a partir das competências gerais da educação básica, previstas na BNCC (^{Brasil, 2018}). Assim, compreende-se que conceitos científicos e matemáticos fazem parte da vida em sociedade. Ou seja, é evidente que o estudante já traz consigo conhecimentos informais, com elementos científicos e matemáticos, experienciados nas suas relações sociais, no seu cotidiano. Porém, para que ocorra, de fato, a inclusão social é necessário articular estes conhecimentos à realidade e às especificidades do estudante com deficiência, considerando o seu contexto familiar e social, com o intuito de potencializar seu desenvolvimento cognitivo.

Na perspectiva da BNCC (^{Brasil, 2018}), a área da Matemática mobiliza o desenvolvimento de competências fundamentais para o letramento matemático: raciocínio, representação, comunicação e argumentação. A aprendizagem de conceitos matemáticos pode promover melhor compreensão de diferentes aspectos da vida em sociedade para os estudantes. A Educação Matemática, percebida aqui como um espaço para a inclusão social, pode potencializar situações do cotidiano por meio de saberes que se mostram necessários ao processo de autonomia, como por exemplo: organização do tempo: as horas, os dias da semana, os meses do ano; organização do espaço: deslocar-se sozinho, chegar de um ponto ao outro. Estes saberes, que se refletem em atividades diárias exigem a compreensão do conceito de número e das operações, como adição, subtração, multiplicação e divisão. Assim, no contexto da pesquisa aqui descrita, cabe destacar que estudantes cegos desenvolvem imagens mentais, conceitos de objetos e quantidades a partir de suas experiências com o mundo tátil (^{Sganzerla & Geller, 2020}, ²⁰²¹). Ou seja, a formação do conceito de número não ocorre por meio de repetição mecânica dos numerais e, sim, pela construção progressiva dos estágios vivenciados no dia a dia, tanto no âmbito social, quanto no educacional.

^{Skovsmose (2001}) já inferia sobre a importância dos conhecimentos matemáticos articulados ao cotidiano, às relações sociais, refletindo que lacunas nestes conhecimentos podem intervir na relação do indivíduo com o mundo, dificultando um posicionamento crítico e a própria tomada de decisões. Neste sentido, defende-se que é direito de estudantes com deficiência, o desenvolvimento cognitivo e social, com a compreensão de conceitos matemáticos importantes para a inclusão efetiva na sociedade.

A partir destas premissas, assume-se a perspectiva da Matemática Social, envolvendo os conceitos que são necessários para se viver na sociedade contemporânea e, que sem os quais, a inclusão é dificultada para pessoas com deficiência, inviabilizando muitas vezes sua inserção na vida social e profissional. Para transitar no mundo social, tornando-se cidadão engajado e interagindo com diversos sujeitos em diferentes espaços, esse aluno precisa dominar determinados conhecimentos que atuem como passaporte para o livre trânsito social (^{Moreira & Silva Junior, 2017}). Um currículo escolar centrado no conhecimento pode favorecer uma política de equidade e igualdade social. Todos os estudantes, independente da rede de ensino que frequentem, devem ter acesso ao conhecimento necessário à sua sobrevivência na sociedade (^{Young, 2016}). Moreira e Silva Junior (²⁰¹⁷) defendem a valorização e a apropriação do conhecimento escolar, principalmente nas escolas públicas, por tratar-se de uma questão de justiça social e de direito de todos. Para os autores, trata-se de lutar contra a insustentável situação de injustiça social cognitiva. Uma situação de injustiça social cognitiva tende a sacrificar os estudantes oriundos da escola pública, que não tem conseguido favorecer o acesso aos conhecimentos hegemônicos e significativos, restringindo-se a conhecimentos pouco importantes para esses sujeitos. Com isto, estes estudantes acabam sendo privados de alcançar novos e mais elevados patamares em suas caminhadas (^{Moreira & Silva Junior, 2017}).

Neste sentido, entende-se que os estudantes, da escola pública da Educação Inclusiva, devem ter o direito ao conhecimento que lhes é fundamental para viver com autonomia e acesso ao mundo profissional. E, um destes conhecimentos, considerados fundamentais, é a compreensão dos conceitos dos Números Naturais e suas operações, bem como a utilização destes conceitos e procedimentos na resolução de situações problemas do dia a dia. Para efetivar a compreensão destes conceitos, a pesquisa descrita neste artigo apoia-se na teoria de ^{Vergnaud (1998}).

Teoria dos Campos Conceituais

Salienta-se que a Teoria dos Campos Conceituais (TCC) de ^{Vergnaud (1998}), teórico cognitivista², defende que a aquisição do conhecimento é afetada pela situação, pelos problemas e pelas ações. O cognitivismo analisa o indivíduo como um ser funcional, em processo de aprendizagem, avaliando a estrutura comunicativa como parte da organização e da interação de conteúdos de suas ideias em uma área reservada de conhecimento, o que vai resultar na aprendizagem.

A TCC apresenta-se como uma importante ferramenta de planejamento de ensino: os professores podem escolher e analisar situações potenciais, detectando dificuldades de identificação ou de evolução conceitual do aluno, projetada para analisar o desenvolvimento e aprender as habilidades complexas dos alunos. Destaca-se que não é uma teoria de ensino, porém, entende-se que esta teoria possa subsidiar a organização de atividades didáticas que levem um estudante a compreensão dos conceitos, levando-o a aplicar estes conhecimentos em situações práticas da sua vida em sociedade. Quando se trata do saber, as habilidades e as aptidões estão envolvidas, e por meio delas, os conhecimentos expressos pelos estudantes podem ser observados e analisados quando estão diante de situações potenciais e, a partir daí, é possível analisar o aprendizado. Quando estudantes são inseridos em uma nova situação, eles buscarão usar o conhecimento adquirido com a sua experiência anterior para resolvê-la da forma mais simples, tentando adaptar-se a esses novos desafios (^{Vergnaud, 1998}).

Segundo ^{Grossi e Bordin (2010}, p. 25), “a ideia de Vergnaud é de que se aprende na trama, não de conceitos linearmente sequenciais, mas no emaranhado de uma rede de muitos conceitos presentes em situações de vida”. Para Vergnaud (¹⁹⁹⁸, p. 181), “o conhecimento de uma pessoa é construído sobre o que ela consegue construir, relacionar e conceituar certas situações ou problemas necessários de diferentes níveis de teorema”.

Ainda de acordo com ^{Vergnaud (1993}), o conhecimento encontra-se organizado em "gavetas", definidas como domínios conceituais. O autor considera o Campo Conceitual como um conjunto de situações, problemas, relacionamentos, estruturas, conceitos e teoremas inter-relacionados. Por exemplo, para um domínio conceitual de estrutura de adição, um conjunto de situações pode exigir adição, subtração ou uma combinação dessas operações. O mesmo ocorre na estrutura de multiplicação, em que o conjunto de situações pode exigir multiplicação, divisão ou uma combinação dessas operações.

Para ^{Vergnaud (1993}, p. 9), uma das vantagens desse método, “(...) é permitir a classificação a partir da análise das tarefas cognitivas e dos procedimentos que podem ser utilizados em cada tarefa”. Um indivíduo precisa de tempo, experiência, maturidade e capacidade de aprendizagem para dominar um determinado Campo Conceitual. As dificuldades conceituais serão superadas quando forem descobertas e enfrentadas, ou seja, isto não acontecerá de forma simultânea. Desta forma, em sua teoria, Vergnaud (¹⁹⁹³) estendeu a atenção dada por Piaget ao desenvolvimento cognitivo para duas direções: 1) tendo como referência o próprio conteúdo matemático; 2) deslocando o interesse das estruturas cognitivas gerais do pensamento para o sujeito em situação.

As concepções e competências dos estudantes vão evoluindo no decorrer do tempo, por meio de situações vivenciadas, sejam elas dentro ou fora da escola. Em uma nova situação, os estudantes aplicam o conhecimento construído por meio de experiências anteriores, buscando adequar-se a esta nova situação de forma adaptada. Sendo assim, o conhecimento em geral é desenvolvido por meio de problemas e situações nas quais o estudante possui alguma experiência, isto é, a origem do conhecimento tem características locais. Para ^{Vergnaud (1998}), os conhecimentos estão fundamentados em conceitos, situações e invariantes operatórios.

Os conceitos não podem ser reduzidos às suas definições, pois um conceito pode ter significado para os alunos apenas por meio da linguagem e dos símbolos envolvidos. Por exemplo, de acordo com ^{Imenes, Jakubovic e Lellis (2007}, p. 8), adição é uma "operação matemática, que corresponde à ideia de adicionar quantidades e adicionar uma quantidade a outra”. A sentença 5 + 3 = 8 significa que a parte é a adição de 5 e 3 e o resultado da soma é 8. Segundo Vergnaud,

(...) a noção de representação não se reduz à noção de símbolo ou de signo, uma vez que ela cobre também a noção de conceito: o estudo do número mostra isso claramente, dado que a escrita simbólica do número é distinta do próprio número. (¹⁹⁹³, p. 18)

Trata-se de uma ideia universal e os educadores devem estar cientes de que a ideia de expressar não se reduz a um sistema de símbolos que aponta de forma direta para o mundo material, mas que o significante expressa diretamente o objeto material. Os alunos podem saber a definição de adição, mas não entender o seu significado, ou ainda serem incapazes de transferi-la para uma situação diferente daquela que estão estudando. ^{Vergnaud (1993}) define o conceito (C) como uma combinação de três grupos: 1) conjunto de situações (S), que dão sentido ao conceito (referência); 2) conjunto de invariantes operatórios (I), que são utilizados para analisar e dominar as situações (o significado), e 3) conjunto de representações simbólicas (R), que são utilizadas para representar os invariantes (o significante). No caso, a fórmula resultante seria C = (S, I, R). Um conjunto de situações do campo conceitual das operações aditivas poderia ser composto de diversas atividades propostas aos estudantes, todas exigindo que eles soubessem adicionar, mas cada uma utilizando uma característica diferente.

O conceito de situação adotado por ^{Vergnaud (1993}) significa que o processo cognitivo e a resposta do sujeito dependem da "situação" que ele enfrenta, ou seja, das tarefas ou atividades propostas ao sujeito. Ainda segundo Vergnaud (¹⁹⁹³) tem-se: 1) variedade: um campo conceitual apresenta várias situações; 2) história: os conhecimentos dos alunos são construídos por situações que eles enfrentaram e dominaram (o que entende-se por conhecimento prévio). Em cada campo conceitual, existe uma grande variedade de situações e o conhecimento dos estudantes é moldado por situações que, aos poucos, vão dominando, sendo elas que darão sentido aos conceitos, tornando-se o ponto de partida para um determinado campo conceitual, requerendo situações diferentes para ter significado.

Da mesma forma, uma única situação requer o exame de vários conceitos, o conhecimento do estudante surge do contato do aluno com a situação e acontece de forma progressiva (^{Vergnaud, 1990}). A situação também é responsável pelo significado dado ao conceito, pois, por meio de diversos contextos, um conceito torna-se significativo. O sujeito possui as habilidades necessárias para resolver o problema quando a situação for relativamente imediata, com um momento para reflexão e exploração que pode ser bem sucedido ou não. Isto ocorre quando, para resolver uma nova situação, todos criam um plano para ela, o qual pode ser retrabalhado até resolver o problema, momento em que os alunos progridem em uma determinada área conceitual. Segundo Vergnaud (¹⁹⁹⁶, p. 167), o conceito de situação não é uma situação didática, mas uma tarefa, e "qualquer situação complexa pode ser analisada como uma combinação de tarefas" para as quais é importante conhecer sua natureza e suas próprias dificuldades. Para o autor, a complexidade está relacionada aos conceitos matemáticos vinculados à situação, mas reconhece que outros fatores, como a linguística e a forma de representar a situação, são importantes para a complexidade. Apesar disso, acredita que o papel desses fatores está subordinado ao próprio conceito matemático. Portanto, torna-se fundamental proporcionar ao estudante a possibilidade de contato com diversas situações, permitindo-lhe refletir sobre as condições de expansão e desenvolvimento cognitivo.

Os processos cognitivos e as respostas do sujeito são funções das situações com as quais ele está lidando. De acordo com ^{Vergnaud (1994}), os alunos dominam certas classes de situações mais simples antes de partir para as mais complexas. Um estudante pode levar vários anos até dominar uma situação simples e então começar a dominar outra mais complexa e durante esse processo, ele passa por: “(...) Situações, palavras, algoritmos e diagramas, símbolos, diagramas e gráficos (...) e aprende ora explorando, ora por repetição, ora representando e simbolizando, ora diferenciando e ora reduzindo coisas a outras” (^{Vergnaud, 1994}, p. 46).

Outro conceito importante neste contexto diz respeito aos invariantes operatórios, descritos como estratégias mentais, que têm por função serem utilizados em diferentes situações, nas quais apresentam semelhanças em alguns aspectos. Podem ser classificados como teorema-em-ação ou conceito-em-ação. Um teorema-em-ação é uma proposição que o sujeito acredita ser verdadeira, ainda que seja em caráter provisório. Um conceito-em-ação “é um conceito considerado pertinente na ação e situação” (^{Vergnaud, 2017}, p. 35). ^{Magina, Campos, Gatirana e Nunes (2008}) ressaltam que o conjunto dos invariantes compreende os objetos, as propriedades e as relações que podem ser conhecidas e usadas pelo sujeito para analisar e denominar as situações, e que expressam a compreensão do educando sobre o conceito, por isso os invariantes dão significado ao conceito.

De acordo com ^{Vergnaud (1996}), o Campo Conceitual das Estruturas Aditivas é um conjunto de situações cujo tratamento envolve uma ou mais adições ou subtrações, ou mesmo uma combinação delas, além de coletar o conjunto. São conceitos, propriedades, teoremas, relações e resultados que nos permitem analisar situações que requerem operações como as matemáticas.

Já o Campo Conceitual da estrutura multiplicativa, segundo ^{Vergnaud (1998}), é o conjunto de situações cujo domínio requer uma ou várias multiplicações ou divisões, é o conjunto dos conceitos e teoremas que permitem analisar essas situações como atividades matemáticas, como por exemplo: multiplicação, divisão, dobro, metade, triplo, funções, razão, taxa, proporção, combinação, área, volume. Para ter o domínio de diversos conceitos das Estruturas Multiplicativas, tais como: adição, multiplicação, proporção, análise combinatória, etc., Vergnaud (²⁰⁰⁹) traz duas categorias: o Isomorfismo de Medidas e o Produto de Medidas.

Percurso Metodológico

A partir da pergunta “Como desenvolver uma sequência didática que possibilite a um estudante cego, dos Anos Iniciais do Ensino Fundamental, compreender e sistematizar as operações de Multiplicação e Divisão no conjunto dos Números Naturais?”, constitui-se esta pesquisa³, por meio de uma abordagem qualitativa, descritiva e exploratória de um estudo de caso, uma vez que, conforme ^{Cervo, Bervian e Silva (2007} p. 62), “o estudo de caso é a pesquisa sobre determinado indivíduo, família, grupo ou comunidade que seja representativo de seu universo, para examinar aspectos variados de sua vida”.

Assim, a pesquisa aqui descrita contempla fatos colhidos da própria realidade de G, um estudante cego congênito do 5º ano do Ensino Fundamental (em 2020), sendo omitida sua identidade para preservar seu anonimato. As intervenções pedagógicas foram realizadas de forma individual, com sessões semanais, totalizando 2 horas, em torno de 30 minutos de atividades, seguido por intervalos de 20 minutos, ao longo de 3 semestres, isto é, durante todo o 5º ano e o primeiro semestre do 6º ano do Ensino Fundamental. Para apoiar estas intervenções, que é o foco do recorte apresentado neste artigo, a pesquisa contou ainda com uma entrevista do professor de G na Associação de Deficientes Visuais de Canoas (ADVIC), além do acompanhamento in loco do aluno na ADVIC e de entrevistas com a mãe de G para conhecer sua história de vida.

Destaca-se, no contexto desta investigação, que a preocupação com o processo é predominante ao resultado e a análise dos dados tende a seguir um processo indutivo, de caráter descritivo (^{Lüdke & André, 2013}).

Salienta-se, ainda, que as transcrições dos diálogos mantêm a fala original dos participantes da pesquisa, sem correção gramatical, para preservar a essência da expressão e da comunicação entre estudante e pesquisadora.

Atividades Didáticas Desenvolvidas nas Intervenções com G: Análise e Discussão dos Resultados

Nas primeiras semanas, foram desenvolvidas com o estudante G, atividades do Campo Conceitual da Estrutura Aditiva (^{Vergnaud, 1998}). O objetivo foi identificar se G já possuía o conceito de número e se resolvia situações simples de adição e subtração com os Números Naturais. Foram desenvolvidos 6 tipos de atividades: composição e decomposição de números com utilização do material dourado; uso do aplicativo Dosvox; jogo de cartas em Braille; resolução de problemas simples envolvendo adição e subtração; jogo de dados em Braille; jogo da Escova (cartas em Braille).

No primeiro encontro, G trouxe a sua caixa que usa como ábaco para realizar adições e subtrações, representando os números com o material dourado. A caixa de G possui repartições com um espaço para colocar as centenas, dezenas e unidades, a unidade de milhar fica de fora da caixa. Ele já compõe, decompõe o número corretamente e nomeia o número por ele composto, utilizando essa caixa adaptada. Na Figura 1, pode-se observar a utilização do material e o diálogo entre G e a pesquisadora ao longo de uma atividade.

A Figura 2 indica o diálogo entre G e a pesquisadora em um exemplo das atividades desenvolvidas com o material dourado, dentre as várias atividades realizadas em diferentes sessões com este material, até que G conseguisse identificar quantas centenas tem no milhar, quantas dezenas tem na centena e quantas unidades tem na dezena. Observa-se que G possui a compreensão de número e domina a composição e decomposição de números com o material dourado.

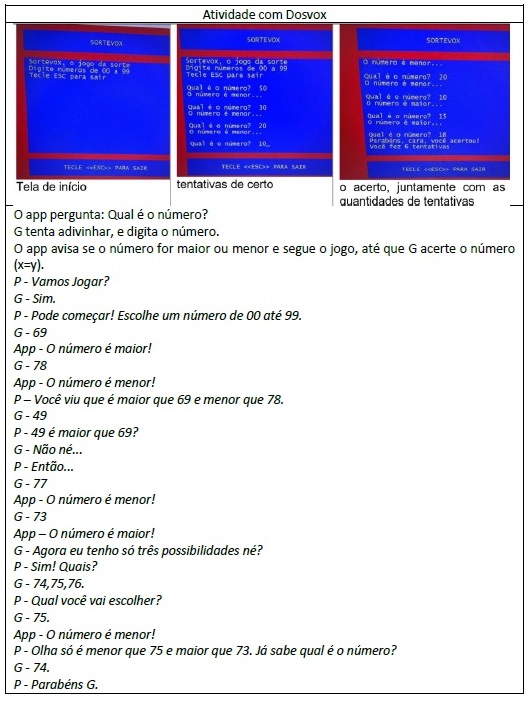
Na Figura 3, apresenta-se um exemplo da atividade com o aplicativo Dosvox, composto por uma interface especializada (^{Dosvox, 2022}), que disponibiliza um pacote com ferramentas matemáticas, como calculadora vocal (Calcuvox), planilha eletrônica (Planivox), editor de textos matemático no padrão Braille (Transcod) e jogos, como por exemplo: Nimvox (jogo dos palitinhos), Julius, o Pirata (longitude e latitude), Cassino (sistema monetário), Contavox (jogo da tabuada). Pode-se observar que x é o número falado pelo app Dosvox e y é o número respondido pelo estudante G, buscando a relação x>y ou x<y ou x=y.

Esta atividade tinha por objetivo identificar se G comparava números, identificando maior, menor ou igual, conforme pode se observar no diálogo entre G e a pesquisadora.

A atividade foi feita em média três vezes a cada encontro com G. Depois de desenvolver várias vezes essa atividade, G começou a se concentrar mais, visando descobrir o número em menos tentativas. Observou-se que o estudante tinha interesse em acertar o número e, aos poucos, conseguiu fazer a dedução correta, dentro da sua sequência numérica lógica. Tudo indica que G está formando os seus invariantes operatórios, quando ele faz a dedução lógica e acerta o número, identificando: maior que; menor que; mais que; menos que; igual a.

Outra atividade desenvolvida com G foi a adição com cartas em braille, como indicado na Figura 4. Cada jogador retira uma carta do baralho, verifica seu valor e compara com a do seu adversário. Primeira jogada: G pega uma carta aleatória do baralho, por exemplo, a carta 10. P pega uma carta aleatória do baralho, por exemplo, a carta 6. Quem fez mais pontos? Logo temos: G → P ↔ 10 → 6.

As atividades com as cartas demonstram a primeira categoria: composição de duas medidas ou mais, segundo a classificação de ^{Vergnaud (1998}) para Campo Conceitual das estruturas aditivas, ou seja, a primeira categoria contempla os problemas em que está presente a ideia de composição de duas medidas, resultando em uma terceira medida, ou ainda, a ideia de parte e todo. Nos diálogos, é possível perceber que G considera mais fácil somar a primeira parcela quando esta é maior que a segunda, o que ficou evidente na escolha da composição das cartas, como por exemplo 6+3=9, e não 3+6=9, 15+7=22 e não o 7+15=22. Em sua primeira resposta, quando a primeira parcela é menor que a segunda, G informa: “Não sei! Tenho que pensar!”.

Este termo “tenho que pensar”, indica que G está montando um esquema mental para achar a solução. Ao montar o esquema mental, G começa a aplicar a propriedade comutativa da adição, dizendo: 6+3 é 9 então 3+6 também é 9. Diante desta situação problema, o estudante G, ao somar seus pontos no jogo de cartas, na tentativa de encontrar o resultado correto, utiliza seus invariantes operatórios. Percebe-se que G está utilizando os seus teoremas-em-ação e conceitos-em-ação, que para ^{Vergnaud (1998}), estão intimamente ligados à rede dos Campos Conceituais das estruturas aditivas.

Outra atividade que auxiliou a compreensão da adição e subtração foi o Jogo da Escova (com cartas em braile). Foram retirados do baralho as cartas com o naipe J, Q, K. O jogo foi realizado entre G e a pesquisadora. Para sortear quem inicia distribuindo as cartas, cada jogador retira uma carta do baralho, quem tiver a carta de valor mais elevado começa a distribui-las, passando três (03) cartas para cada jogador, uma a uma, em seguida colocará quatro (04) cartas abertas na mesa, a sobra do baralho é colocada ao lado do carteador com a face voltada para baixo. O primeiro jogador a iniciar, deverá procurar uma carta em sua mão que somada a uma ou mais das cartas da mesa, tenha um total de 15. Por exemplo: G tem em suas mãos um Ás, um 7 e um 4. Na mesa, estão abertos dois 10, um Ás e um 8 (Figura 5).

Neste caso, G poderá fazer as seguintes jogadas:

Caso ele não consiga pegar nenhuma carta da mesa, deve simplesmente descartar na mesa uma das cartas de sua mão.

Se G conseguir pegar todas as cartas restantes na mesa de uma única vez, por exemplo: Na mesa, havia um 7 e um 5 e o jogador possuía um 3 em sua mão, sendo que 7+5+3=15, G faz uma escova. Ao colocar na sua frente as cartas pegas, ele deverá colocar uma delas com a face voltada para cima e perpendicular ao monte de cartas voltadas para baixo. Será o sinal de que ele fez uma escova. Para cada escova feita, o mesmo procedimento deverá ser repetido. Quando os jogadores tiverem utilizado suas 3 cartas, uma nova mão de 3 cartas é distribuída, utilizando o monte que havia sido posto de lado. A partida prossegue da mesma maneira até que o monte de cartas termine e somente aí é feita a contabilização dos pontos da rodada. A contabilização dos pontos: cada escova vale 10 pontos; cada carta vale o seu respectivo valor.

Na continuidade do jogo, G deve avaliar a melhor alternativa para fazer a escova. A figura 6 reporta esta situação com o diálogo entre G e a pesquisadora, uma vez que cada partida serve de subsídio para intervenções da pesquisadora, para que a estrutura do campo conceitual aditivo seja bem construída pelo aluno, montando seus esquemas e verbalizando.

As jogadas foram realizadas até terminar as cartas do baralho, sendo que G ganhou o jogo. Sempre realizando a adição em que a primeira parcela fosse maior que a segunda, assim organizava as cartas. Com o jogo da escova adaptada do 15, por meio da intervenção da pesquisadora, foram trabalhadas todas as seis categorias dos Campos Conceituais das estruturas aditivas (^{Vergnaud, 1998}). Assim, foi possível verificar que G organiza os esquemas adequados para a solução de situações problemas. Considerando que o aluno é cego, a representação e comunicação de seus esquemas mentais são feitas oralmente e/ou com o uso do material tátil.

Na atividade da Figura 6, percebe-se que G está com a estrutura da adição finalizada, seguindo as categorias descritas a seguir:

Segundo ^{Vergnaud (1993}), o Campo Conceitual de estrutura aditiva é o conjunto de situações cujo domínio requer uma ou várias adições e subtrações ou uma combinação de tais operações, e o conjunto dos conceitos e teoremas que permitem analisar essas situações como tarefas matemáticas. O estudante G, no decorrer da pesquisa demonstra facilidade na primeira e na segunda categorias, sendo que na terceira categoria precisa de mais reflexão para resolver as situações referentes a ela, no que tange “a mais”, “a menos”, e a partir das categorias 4, 5 e 6, as transformações começam a aparecer de forma mais explícita, dificultando a sua esquematização. Estes aspectos foram trabalhados posteriormente com outras atividades.

Foram desenvolvidos com G, 5 tipos de atividades do campo multiplicativo: Jogo do General (para o conceito de multiplicar); Construção das tabuadas do 2 ao 10 e depois da tabuada do 1; Atividades de combinações com o campo multiplicativo - discreto- discreto; Atividades do campo multiplicativo - contínuo-contínuo; Resolução de problemas. As atividades do Jogo do General e a construção das tabuadas se caracterizam como isomorfismo de medidas e as atividades de combinação discreto-discreto e as atividades do produto contínuo-contínuo se caracterizam como produto de medidas.

As multiplicações com o fator multiplicando maior que 1 e menor que 10 tiveram todas as atividades realizadas com o apoio de materiais táteis: Fator 2 - motos de brinquedo (2 rodas); Fator 3 - Sorvetes de plástico (3 bolas); Fator 4 - Carrinhos de brinquedo (4 rodas); Fator 5 - Luvas de motociclista (5 dedos); Fator 6, 7, 8, 9 e 10 - Ábaco. A Figura 7 contempla um exemplo das atividades para a construção da tabuada do 3 e o diálogo entre G e a pesquisadora ao longo desta atividade.

O estudante G estava no 5º ano e já conhecia as expressões multiplicação e divisão. Como tarefa para a escola regular, G precisava “memorizar a tabuada de (vezes)”, sem o domínio da TCC da estrutura multiplicativa. Considerando que no jogo de General G já multiplicativa por meio das adições reiterativas, considerou-se que a multiplicação deixou de ser apenas uma memorização e passou a ter um significado. Assim, foi trabalhada a primeira classe do isomorfismo de medidas: na multiplicação conhecendo o valor unitário e outras duas quantidades de dois tipos de medidas (sorvetes e bolas), conforme destaca-se o diálogo a seguir entre G e a pesquisadora:

P - Quantas bolas tem um sorvete? G - Três. 3 sabores diferentes. Chocolate, morango e creme. P- 1x3 = 3. Um sorvete tem três bolas. Quantas bolas tem dois sorvetes? Pode pegar para contar. G - 3+3=6. Dois sorvetes têm 6 bolas.

Na segunda classe do isomorfismo de medidas: divisão - busca do valor unitário, como se verifica nas falas:

P - Se eu pegar 4 sorvetes e contar, e tiver ao todo 12 bolas, quantas bolas deverá ter cada sorvete? G - Não sei! Vou contar com 4 sorvetes, porque cada um já tem três bolas. G - Tem mesmo, quatro sorvetes têm 12 bolas mesmo. Então cada sorvete tem três bolas.

Na terceira classe do isomorfismo de medidas: a busca da quantidade de medidas, destaca-se no diálogo:

P - E se eu tiver 24 bolas e quiser montar sorvetes de três bolas, como eu fazer? G - Vou fazer os montinhos de três par ver quantos vão dá. Oh deu 8. Porque 8x3=24 então 24:8=3.

Foram trabalhadas, também, situações problemas sem o uso do material tátil, sendo que seu uso ocorreu somente quando foi necessário, como demonstra-se no diálogo a seguir:

P - João tem um álbum de figurinhas com 10 páginas, cada página tem 4 figurinhas. Quantas figurinhas ele precisa para preencher o álbum? G - Neste álbum tem 10 páginas, cada página tem 4 figurinhas, então precisa de 40. P - Por que 40? G - Porque é 10x4=40 P - Ana foi ao cinema com suas 24 amigas, cada fileira do cinema tem 6 cadeiras. Quantas fileiras as amigas ocuparam? G - 24:6? P - Isso. G -24:6=4, porque 6x4=24. P - Eu tenho 8 balas e quero dividir para 8 pessoas. Quantas balas cada um ficará? G - Vou colocar nos potes. 8:8=1, porque 8x1=8. P - Rodrigo tem 12 balas, e precisa dividir igualmente para os seus 4 amigos, quantas balas Rodrigo dará para cada amigo? G - Tá, é só pegar 12 e o dividir por 4, 12 ÷ 4 é 3 porque 4 × 3 é 12. P - Eu tenho 15 balas e quero dividir para 5 amigos, quantas balas ficará para cada amigo? G - Vai dar 3 né, por que 3 × 5 e 15. P - Gabriel tem 10 reais e quero dividir igualmente esse dinheiro entre ele e sua avó Iaiá, quanto receberá cada um? G - 5 reais. 10:2=5, porque 2x5=10. P - Eu ganhei 20 balas, comi 8, e as que sobraram eu dividi igualmente entre 3 amigas, quantas balas cada amiga recebeu? G - 12:3 é 4 porque e 3x4=12. P - Eu tenho 20 balas e comi 5, preciso dividir o restante com 3 pessoas, quanto ganha a cada um? G - Eu preciso tirar 5, né? P - Quantos sobraram? G - 15. Dividir para 3 pessoas, preciso pegar os 3 potes. P - Tu vai pegar 3 potes? G - Vou né, para contar. 15:3 é 5 e sobra 0. 15:3=5, porque 3x5=15. Agora, você escolhe um número. P - 12, você quer dividir 12 em quantas partes? G - Em 4. Porque 12:4=3 e 4x3=12, e 3x4=12 também. P - E se eu dividir por 2 G - 12:2=6, porque 2x6=12.

O estudante G mostrou compreensão na TCC na estrutura multiplicativa em isomorfismo de medidas. Por exigência da escola, G memorizou a tabuada. Contudo, atualmente, o aluno G constrói a tabuada da multiplicação e divisão, quando tem dúvida, utiliza o material tátil. O isomorfismo de medidas foi trabalhado apenas em conjunto dos Números Naturais com quantidades discretas. Após o trabalho com isomorfismo de medidas, foram abordados os produtos de medidas, com material tátil. A figura 8 traz o diálogo de uma atividade envolvendo duas classes de problemas: multiplicação e divisão, com a apresentação e manuseio do material, com meninos com diferentes tipos de bonés e meninas com diferentes tipos de penteados.

Em relação as situações problemas que envolveram um isomorfismo de medida na multiplicação e divisão, o estudante G aplicou corretamente a TCC da estrutura multiplicativa na classe produto de medidas: produto discreto-discreto. Para a atividade, foi usado material tátil, de acordo com a sua preferência, que fica explícita sempre que G diz: “Vou pegar o material”, “Vou fazer montinhos”. No momento em que está conceitualizando, G diz: “Estou pensando”, isto é, relacionando seus invariantes operatórios, “Vai aumentar é multiplicação”, “Vai diminuir é divisão”, seus teoremas em ação.

No seu “Estou pensando”, G está analisando um conjunto de situações, relacionando seus teoremas-em-ação e conceitos-em-ação. A comunicação do que pensou “esquema feito” comunica oralmente, manipulando o material ou, ainda, escrevendo em braille. Escrever em braille não é a sua preferência, segundo G, porque “demora muito para registrar”.

Entende-se que o Campo Conceitual da estrutura multiplicativa está dominando, mas ainda necessitando mais situações problemas a serem solucionados para fixar a noção construída pelo aluno G (figura 9).

As atividades desenvolvidas com o aluno G confirmam a teoria de ^{Vergnaud (1998}). Para a formação e o desenvolvimento de um conceito durante a aprendizagem dos educandos, Vergnaud (¹⁹⁹⁸) ressalta a importância de considerar que o conceito é formado por uma terna de: conjunto de situações, conjunto de invariantes operatórios e conjunto de representações. Para tanto, o aluno G já domina a terna de conceito quando consegue analisar uma situação, fazer esquemas utilizando seus invariantes operatórios e expondo sua representação, por meio de material tátil e/ou oralmente.

Neste contexto, entende-se ser fundamental a seleção de recursos didáticos que destaquem aspectos táteis e auditivos, pois o aprendizado do estudante cego se constitui a partir dos sentidos remanescentes como tato, audição e olfato. Desta forma, contemplar o uso de materiais que facilitem a discriminação e/ou identificação do tamanho, textura, volume, peso, poderá aguçar sua curiosidade e vontade de aprender (^{Sganzerla & Geller, 2021}).

Um ponto que se pretendeu sempre manter ao longo das intervenções pedagógicas realizadas com G foi focar em seu potencial cognitivo, articulando o seu acesso aos conhecimentos matemáticos de forma contextualizada, considerando, por exemplo, elementos que o estudante poderá levar para suas relações sociais, como os jogos de cartas, e não condicionando as atividades propostas ao fato de que G é cego. Ele é um menino de 11 anos, curioso, que se mostra feliz quando percebe que aprendeu algo novo, portanto, é seu direito como cidadão desenvolver-se cognitiva e socialmente e cabe à educação um papel fundamental ao romper barreiras e favorecer a equidade e a igualdade social.

Conclusões

Neste artigo, busca-se refletir sobre as intervenções pedagógicas, envolvendo distintas estratégias para a aprendizagem de conceitos matemáticos. Para tanto, foram utilizados jogos, materiais digitais e concretos ou manipuláveis, com o intuito de implementar e analisar uma sequência didática para o desenvolvimento dos Campos Conceituais das estruturas aditivas e multiplicativas no conjunto dos Números Naturais.

Ao longo do processo, G, um estudante cego congênito do Ensino Fundamental, que inicialmente compreendia o conceito de número, passa a organizar os esquemas adequadamente para a solução de situações problemas envolvendo os Campos Conceituais das estruturas aditivas e multiplicativas.

Destaca-se que não se pretende, com esta pesquisa, assumir um viés prescritivo, mas entende-se que compor uma sequência didática possa contribuir com o processo de desenvolvimento de noções matemáticas. Entende-se, ainda, que na perspectiva da educação inclusiva não exista um formato único, o que não impede que estratégias já exploradas não possam ser utilizadas, desde que se respeite o ritmo de aprendizagem de cada estudante.