1. Introducción
La enseñanza del concepto pendiente es de preocupación por parte de diversos investigadores (Moore-Russo, Conner & Rugg, 2011; Stump, 1999; Zaslavsky, Sela & Leron, 2002), debido a su complejidad y relación con otros conceptos de la matemática, por ejemplo, razón de cambio y derivada.
La pendiente juega un papel crucial en diferentes ramas de la matemática, como lo es el cálculo, trigonometría, geometría y algebra, de ahí su relevancia de enseñar su significado y cálculo en educación básica (en México, en educación secundaria). Para Nagle et al. (2013), este concepto es relevante para construir un pensamiento matemático más avanzados y es base para comprender su construcción en diversos contextos y escenarios de la matemáticas. Por su parte, en México, la SEP (2004, p. 124) plantea que “casi todas las matemáticas de la preparatoria […] requieren [de un buen] lenguaje del álgebra para modelar situaciones y resolver problemas, así como para expresar conceptos y operar con ellos en niveles cada vez más abstractos”, sin dejar de lado que “álgebra, más que cualquier otra parte de las matemáticas en la educación secundaria, representa la transición entre la aritmética y la geometría elementales de la primaria y las matemáticas de grados superiores” (p. 124).
Investigadores en educación matemática consideran que los estudiantes presentan dificultades en torno a comprender y calcular la pendiente de rectas cartesianas (Lobato & Thanheiser, 2002; Moore-Russo et al., 2011; Nagle, Moore-Russo, Viglietti & Martin, 2013), en particular, Moore-Russo et al. (2011) afirman que los jóvenes no logran comprender este concepto dada su complejidad; por su parte, Walter y Gerson (2007) mencionan que esta problemática se agudiza debido a que en ocasiones se usan significados coloquiales, como inclinación, declive, empinada, entro otros, para hace referencia a la pendiente o posición de la recta. De acuerdo con lo anterior, “los profesores de matemáticas en servicio… necesitan oportunidades para examinar el concepto de pendiente, reflexionar sobre su definición, [y] construir relaciones entre sus diversas representaciones” (Stump, 1999, p. 142).
En la investigación desarrollada por Teuscher y Reys (2010) se sugiere que los profesores deben ayudar a sus estudiantes a comprender las diferencias y relaciones que existen entre pendiente, razón de cambio e inclinación de la recta. Por ello, las tareas seleccionadas por parte de los docentes son cruciales, Wagener (2009) sugiere que las tareas planteados a los estudiantes deben ser de mayor demanda cognitiva más que de memorización, ya que estas últimas no llevan a compresión del concepto de pendiente. Un tarea de memorización es pedir a los estudiantes recordar la fórmula, por ejemplo, lo que sube entre lo que avanza, para calcular la pendiente a partir de dos puntos dados. Además, como asegura Wagener, este tipo de tareas no les permite a los estudiantes hacer conexiones o determinar la relevancia de la pendiente en situaciones de la vida cotidiana.
Aunque la literatura de investigación hace valiosas contribuciones en torno a la comprensión de la pendiente y razón de cambio en rectas cartesianas (Nagle et al., 2013; Stanton & Moore-Russo, 2012), expertos afirman que el concepto ha recibido poca atención; para Stanton y Moore-Russo (2012), se sabe muy poco de cómo es abordado en la clase de matemáticas y cómo está planteado en el currículum matemático. De acuerdo con lo antes expuestos, el presente estudio tiene como objetivo identificar cuál es la propuesta curricular en México para enseñar el concepto de pendiente en tercer grado de educación secundaría (estudiantes entre 14 y 15 años de edad); en particular, identificar el tipo de actividades didácticas y su relación con el significado de pendiente.
2. Marco de Referencia
La pendiente es un concepto matemático clave con implicaciones que van más allá de su uso algebraico, como indicado de la inclinación de una recta trazada en el plano cartesiano (Nagle et al., 2013; Lobato & Thanheiser, 2002; Stump, 2001). Aunque suele ser enseñada como el ángulo de inclinación de una recta respeto al eje de abscisas, investigadores como Stump (1999, 2001) y Moore-Russo et al. (2011) mencionan que la pendiente tiene diferentes representaciones (o significados) y propiedades, las cuales están dadas en función de diversos contextos de la matemática. De acuerdo con Moore-Russo et al. (2011), Nagle et al. (2013), Stanton & Moore-Russo (2012), la pendiente es definida o representada como:
Razón geométrica: lo que sube entre lo que avanza, así como el desplazamiento vertical sobre el desplazamiento horizontal.
Razón algebraica: el cambio en y sobre el cambio en x; representación de la razón con expresiones algebraicas ∆y/∆x o (y2-y1)/(x2-x1).
Propiedad física: la propiedad de la recta a menudo descrita usando expresiones como “empinada” [steepness] (“acostada” [slant], “alta” [pitch], “qué tan alta” o “sube”.
Propiedad funcional: la tasa de cambio constante entre variables.
Coeficiente paramétrico: el coeficiente m en la ecuación y=mx+b. Para Nagle et al. (2013), el coeficiente m también en la ecuación y2-y1=m(x2-x1).
Concepción trigonométrica: la tangente del ángulo de inclinación de una recta; el componente de dirección de un vector.
Concepción en cálculo: límite, derivada y la recta tangente a una curva en un punto dado.
Situación del mundo real: estática, situación física (e.g., rampas). Dinámica, situación funcional (e.g., la distancia en función del tiempo).
Propiedad de determinación: la propiedad que determina si las rectas son paralelas o perpendiculares; la propiedad con la que se puede determinar una recta si se tiene un punto dado.
Indicador de comportamiento: el número real con signo que indica el crecimiento, decrecimiento, tendencias horizontales de la recta; el número real con magnitud que indica la cantidad de crecimiento/decrecimiento de la recta; el número real indicando que, si es positivo o negativo, la recta debe intersectar con el eje x.
Constante lineal: La propiedad que no se ve afectada por la translación [“Property that is unaffected by translation”]; la propiedad constante exclusiva de figuras “rectas”; la propiedad constante independientemente de la representación.
3. Metodología
El presente estudio es de corte cualitativo y tiene una aproximación descriptiva en torno a la propuesta curricular de matemáticas en México (Álvarez, 2003; Cohen, Manion & Morrison, 2007; Schoenfeld, 2007). La elección de esta perspectiva permite hacer un análisis documento de estudios sobre el concepto de pendiente, así como identificar las sugerencias didácticas que ofrece el currículum escolar mexicano para dar cuenta de su relevancia en educación secundaria. De acuerdo con lo antes expuesto, esta investigación cumple con los criterios señalados por Schoenfeld (2007), es decir, el estudio toma en cuenta los criterios de generalidad -o de alcance-, importancia y fiabilidad:
• La generalidad se refiere al contexto situación en el cual se desarrolla la investigación, así como la amplitud y alcance de los resultados;
• La importancia está relacionada con los argumentos en torno a cuál es la importancia de la investigación, en el sentido de si los resultados son pertinentes y si contribuyen a la disciplina;
• La fidelidad, como criterio, está centrada en la credibilidad de los resultados de la investigación.
El estudio está centrado en hacer una revisión de tres documentos relacionados con el currículum escolar para matemáticas en tercer grado de educación secundaria en México: Planes y programas de estudios 2006 (SEP, 2006) y 2011 (SEP, 2011) y Orientaciones didácticas 2017 (SEP, 2017), ya que estos documentos oficiales son recursos fundamentales, siendo 2017 el vigente, del profesor para enseñar matemáticas; en ellos están planteados los contenidos a enseñar en educación y los aprendizajes a lograr, así como las sugerencias didácticas de cómo abordar estos contenidos. Se tomó como método el estudio de casos (Cohen et al., 2007; Rodríguez, Gil & García, 1999), cuya finalidad es bordar ejemplos específicos en los cuales se hace referencia a un sistema de estudio delimitado, como lo es el currículum escolar mexicano (Cohen et al., 2007).
El análisis se hizo tomando como referente Miles, Huberman y Saldaña (2014) y Miles y Huberman (2007), se diseñaron dos tipos de categorías inductivas para organizar e interpretar los datos recabados: a) Información conceptual del pendiente; b) Sugerencias o actividades didácticas para construir o trabajar la pendiente. En este análisis se identificaron ideas relacionadas con la pendiente, tanto conceptuales como procedimentales. La validez tanto de las categorías y resultados se obtuvo a partir de un proceso de triangulación entre los responsables del estudio (Cohen et al., 2007), se buscó que hubiera coherencia en la interpretación de los datos en cada una de la categorías (Zodik & Zaslavsky, 2008).
4. Resultados
En México, la Secretaría de Educación Pública (SEP), a partir del 2006, propuso el Plan y programa de estudios en cual están institucionalizados los saberes matemáticos que los estudiantes de educación básica (preescolar, primaria y secundaria) deben tener para continuar con su formación escolar (Chevallard, 1999), posteriormente hace modificaciones y propone el nuevo Plan y programas 2011 (SEP, 2011) y Orientaciones didácticas 2017 (SEP, 2017), siendo este último el vigente. En nivel secundaria, uno de estos saberes es el concepto de pendiente, lo plantea en segundo y tercer grado, pero en cada grado con diferentes objetivos: en segundo se trabaja en el contexto del álgebra mediante funciones lineales, y en tercer grado el objetivo de aprendizaje gira en torno a la interpretación geométrica del valor de la pendiente de la recta trazada en un sistema de coordenadas cartesianas.
Para este último objetivo se toma como referente la razón de cambio ("Cálculo y análisis de la razón de cambio de un proceso o fenómeno que se modela como una función lineal. Identificación de la relación entre dicha razón y la inclinación o pendiente de la recta que la representa", SEP, 2011, p. 50), de modo que ambos conceptos quedan como sinónimos entre sí, por ejemplo, se dice que “los alumnos notarán que… inclinación (pendiente o razón de cambio) [de una recta] es constante (SEP, 2017). En particular, de acuerdo con los Planes y programas 2006 y 2011, el concepto de pendiente es introducido al estudiar la razón de cambio en funciones lineales y para vincularlo con la inclinación de la recta. Lo anterior muestra que la pendiente es vista en términos de razón algebraica, el cambio en y sobre el cambio en x (Moore-Russo et al., 2011; Nagle et al., 2013; Stanton & Moore-Russo, 2012).
La razón de cabio, como pendiente, es dada como una comparación de dos variables y puede ser estudiada -en el sistema de coordenadas cartesianas- cuando hay una relación funcional entre esas variables (SEP, 2006, 2011); en otras palabras, cuando a cada valor de la variable dentro del dominio le corresponde uno y sólo un valor de la otra variable dentro del contradominio. En relación con esto, la SEP (2006, p. 110) plantea lo siguiente: "siempre que dos variables (magnitudes) están conectadas mediante una relación funcional, se puede estudiar el cambio relativo de una de las variables respecto de la otra, es decir, se pueden determinar y analizar las razones de cambio del fenómeno".
Al tener la razón de cambio como una medida de comparación de dos variables a partir de sus unidades de cambio, se espera darle significado de acuerdo con el proceso o fenómeno representado en recta trazadas en el sistema de coordenadas cartesianas. Así, el Plan y programas de estudios deja entrever que la razón de cambio (como pendiente) es una característica o propiedad de la recta, que refiere a la medida de cambio del fenómeno o proceso representado por la recta (cómo una variable se modifica en relación a la otra), lo cual coincide con Moore-Russo et al. (2011), Nagle et al. (2013) y Stanton y Moore-Russo (2012), al interpretar la pendiente en términos de razón algebraica.
Para calcular la razón de cambio de un fenómeno físico que involucra la relación de las variables, por ejemplo, tiempo-costo, el currículum (SEP, 2006) sugiere representar esta relación con una recta trazada en un sistema de coordenadas cartesianas (Figura 1). En este sentido, introduce y usa la representación de la razón de cambio como el cambio en y sobre el cambio en x, donde estos cambios se refiere a la variación (incremento) que existe entre dos valores de cada variable, así, en un lenguaje algebraico se tiene que la razón de cambio es igual a (y2-y1)/(x2-x1).
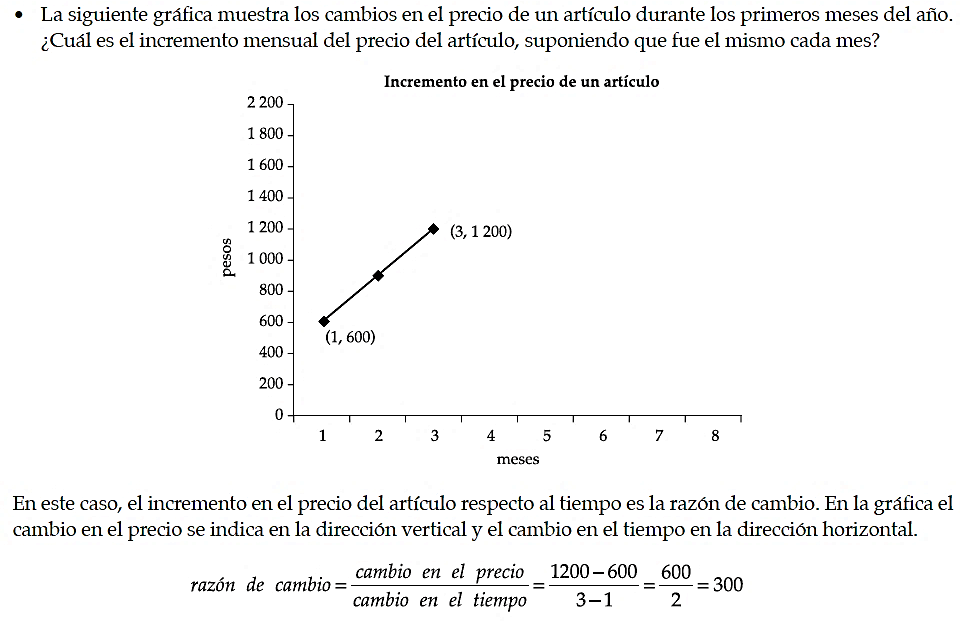
Figura 1: Actividad sugerida en el currículum escolar para trabajar la pendiente de una recta como razón de cambio (SEP, 2006, pp. 110-111).
De acuerdo con la Figura 1, el currículum (SEP, 2006) incluye una explicación de cómo en la recta se da el cambio de cada variable, sin una representación geométrica: “en la gráfica el cambio de precio se indica en la dirección vertical y el cambio en el tiempo en la dirección horizontal” (p. 110). Lo anterior muestra que la pendiente es vista como razón geométrica a partir su representación algebraica (Moore-Russo et al., 2011; Nagle et al., 2013; Stanton & Moore-Russo, 2012); sin embargo, no se precisa que tales cambios o variación deben coincidir de manera que se obtenga en su representación geométrica un triángulo rectángulo con vértices en los puntos (x2,y2) y (x2,y1) de la recta y (x1,y1), de modo que el lado vertical se refiere a y2-y1, y el lado horizontal a x2-x1.
Así, la pendiente como razón geométrica y algebraica se refiere al cambio que se da en la variable dependiente por cada unidad de cambio de la variable independiente; por ejemplo, en la Actividad de la Figura 1 la razón 300 significa que por cada mes que pasa hay un incremento de 300 pesos en el costo del producto (SEP, 2006).
En esta Actividad, para calcular la pendiente mediante la razón de cambio (algebraica), se sugiere conocer las coordenadas de otros puntos de la recta, por ejemplo, determinar el costo de producto el sexto mes.
Al tener 300 como la variación del costo del artículo por mes y dado que (3,1200) y (6,y2) pertenecen a la recta, se tiene que 300= (y2-1200)/(6-3), de modo que y2=300(3)+1200, así (6,y2=2100). En este sentido, cualquier punto a encontrar de la recta, dado la razón de cambio y un punto, tiene las coordenadas {(x,y)|y=300x+300}, lo que hace referencia es la ecuación punto-pendiente de la recta: y-y1=m(x-x1) (Rees, 2003). Lo anterior muestra que el currículum (SEP, 2006) la pendiente también aparece como coeficiente paramétrico (Nagle et al., 2013).
Además de la actividad sugerida en la Figura 1, el Plan y programas de estudios (SEP, 2006) proponen otras cuya finalidad es reforzar y darle sentido a la noción de razón de cambio y vincular la con la pendiente de una recta; en ellas, está la tasa de crecimiento y la velocidad: “la razón de cambio de la distancia en relación con el tiempo se llama velocidad” (p. 110), aunque no se menciona cómo interpretarlo de manera simbólica y algebraica. En algunas de estas Actividades se busca identificar y argumentar por qué la pendiente, como razón de cambio, es la misma en rectas paralelas cartesianas. Lo anterior muestra que el curriculum también plantea la propiedad de determinación de (Moore-Russo et al., 2011; Nagle et al., 2013; Stanton & Moore-Russo, 2012).
5. Conclusiones
Los resultados muestran que los tres documentos oficiales, Planes y programas de estudios 2006 y 2011 y Orientaciones didácticas 2017 (SEP, 2006, 2011, 2017), tienen un papel importante en la compresión y cálculo de la pendiente. Los dos primeros documentan se mantienen igual en cuanto al tipo de aprendizaje esperado en los estudiantes en torno al concepto de pendiente, sin embargo, los tres plantea trabajar en tercer grado de educación secundaria la pendiente en términos de razón de cambio; en términos geométricos y algebraicos (Moore-Russo et al., 2011; Nagle et al., 2013; Stanton & Moore-Russo, 2012), se encontró que el currículum refiere a la propiedad de determinación y coeficiente paramétrico de acuerdo con estos autores. Sin embargo, los fenómenos propuestos en las actividades involucran unidades de medida no homogéneas, lo cual podría generar dificultades de comprensión o errores conceptuales en los estudiantes, en particular, determinar que la pendiente vista como razón de cambio involucra unidades de medida. De acuerdo con Rees (2003), ésta carece de unidades, solo es un valor numérico que se refiere a la posición de la recta recto respecto al eje de las abscisas.
Para evitar ambigüedades o posibles dificultades de compresión en los estudiantes, es fundamental explicitar cómo la razón de cambio e inclinación se vinculan con la pendiente. En relación con la pendiente e inclinación de la recta, el curriculum (SEP, 2006, 2011, 2017) sugiere relacionar ambos conceptos, pero no sugiere cómo hacer, solo se centra en la razón de cambio. Asimismo, es necesario que la propuesta curricular plantea actividades en las que se manejen unidades de medidas homogéneas con la finalidad de que le ayuden al niños a comprender la pendiente como un número, así como identificar la relación de este número con la posición de la recta en el plano cartesiano o con situaciones dadas en la vida cotidiana.















