Serviços Personalizados
Journal
Artigo
Indicadores
Links relacionados
Compartilhar
Silva Lusitana
versão impressa ISSN 0870-6352
Silva Lus. vol.19 no.1 Lisboa 2011
Ecomosaic Composition and Expected Utility Indices
José Pinto Casquilho
Researcher
Centro de Ecologia Aplicada "Prof. Baeta Neves" (CEABN). Instituto Superior de Agronomia. Tapada da Ajuda, 1349-017 LISBOA
Abstract
Forest planning is a major issue for future development of regions, and landscape changes reflect to a large extent land-use/cover patterns related to economic and option's values as driving forces. Managing for reducing variability may have high costs of stability or resilience. Decision theory relies on maximizing an average or expected value of a preference pattern expressed by utility functions. In this paper I discuss quantitative indices bonded to expected utility concepts that may provide diagnosis tools and become generators of the relative extension of the different habitats that compose an ecomosaic. The indices combine characteristic values and context values in contributive values, defined in a normalized measure space. Scenarios of composition for forest planning in the region of Nisa, Portugal, are discussed and benchmarked with standard measures: mean economic value, related to recover costs of forest habitats, and landscape diversity. Situation theory and relevance theory are axiomatic baselines of the abductive process and heuristic procedures here developed.
Key words: Forest planning; decision theory; contributive values; heuristic procedure; Nisa, Portugal
Composição de Ecomosaicos e Índices de Utilidade Esperada
Sumário
O planeamento florestal integrado é fundamental para o desenvolvimento futuro das regiões e as alterações na paisagem reflectem em grande medida padrões de uso da terra e de cobertos florestais relacionados com valores económicos e de opção actuando como forças motrizes. Gerir para reduzir a variabilidade pode ter altos custos de estabilidade ou de resiliência. A teoria da decisão baseia-se na maximização do valor médio ou esperado de um padrão de preferências expresso por funções de utilidade. Neste artigo discutem-se índices quantitativos que podem fornecer ferramentas de diagnóstico e ser geradores da extensão relativa dos diferentes habitats que compõem um ecomosaico. Os índices combinam valores característicos com valores de contexto em valores contributivos definidos num espaço normalizado de medida. Discutem-se cenários de composição de planeamento florestal para a região de Nisa, Portugal, aferidos com medidas padronizadas: valor económico médio, relacionado com custos de reconstituição de habitats, e diversidade paisagística. A teoria da situação e a teoria da relevância são invocadas como linhas axiomáticas de base do procedimento heurístico e do processo abdutivo aqui apresentados.
Palavras-chave: Planeamento florestal; teoria da decisão; valores contributivos; procedimento heurístico; Nisa, Portugal
Composition d'Ecomosaïques et Indices de l'Utilité Attendue
Résumé
La planification forestièreest un enjeu majeur pour le développement futur des régions et les changements de paysage reflètent dans une large mesure les forces motrices rapportés avec des valeurs économiques et d'option en normes d'utilisation de la terre et des couverts forestiers. Ménager pour réduire la variabilité peut avoir des frais élevés de stabilité ou de résilience. La théorie de la décision s'appuie sur la maximisation de la valeur moyenne ou attendue d'un schéma de préférences exprimée par des fonctions d'utilité. Dans cet article on discute des indices quantitatives, fonctions d'utilité attendue, qui peuvent fournir des outils de diagnostic et générer des scénarios concernant l'extension relative des habitats qui composent un ecomosaic. Les indices combinent les valeurs caractéristiques et valeurs de contexte dans des valeurs contributives définies dans un espace normalisé de mesure. On discute aussi des scénarios de composition pour la région de Nisa, Portugal, comparés en termes de mesures standard: la valeur économique moyenne liée aux frais de reconstituer les habitats et la diversité du paysage. La théorie de la situation et la théorie de la pertinence sont des lignes axiomatiques de la procédure heuristique et de la démarche abductive ici présentées.
Mots clés: Planification forestière; théorie de la décision; valeurs contributives; procédure heuristique; Nisa, Portugal
[...] the work to be carried out, aiming at multiple objectives, is of multiple-use, in the broadest sense of the word, and materializes associating diverse functions in the same areas and partitioning areas by separate functions or function groups, always in a mosaic that ensures the desired sustainable and balanced flow of goods and indirect benefits.
A. M. de Azevedo Gomes[1]
Introduction
Forest planning of a region is a major issue that begins with defining main categories of habitats or forest types presumed to be ecologically suitable and economically relevant, eventually assigned to specific areas. Such an utterance provides a rationale where planning for the future is considered valuable, anchored to a concept of knowledge as source of progress, and progress is conceived linked to clues of enhancing productivity and promoting sustainability and diversity of the forest landscape, perceived as an integrated object, described as a mosaic - a metonymy of a territory engraved as a tile inspired by the muse. Forest planning in Portugal has long been characterized as an integrated approach, a multidisciplinary task, rooting at both socioeconomic and ecological contexts (ALVES, 1982).
Problems arise at many levels, but may be the first level to be considered is what PEARCE (2001) points out as: sustainable forests pay, but unsustainable forests pay more, although it is potentially large, but unknown, the value of the forest stock as scientific information that may be lost if irreversible deforestation continues apace. It is referred that harvesting activities might be scheduled over the landscape so that older forests might be sustained over time and arranged in large enough patches to be effective for wildlife habitat and natural ecological processes (HOGANSON et al., 2004). Under an economic perspective, the crude benchmark rule for conservation of resources is that the economic value for conservation must exceed the economic value of conversion.
Economists in general think of values as instrumental quantities, meaning that they are derived from some objective function, the goal or purpose that is being thought, as for the case of maximizing human welfare or utility (PEARCE and PEARCE, 2001).
In mixed forests diversity has to be considered as they are managed not only for timber production but also for recreation, ecology, diversity, aesthetics, game, etc (GONÇALVES et al., 2010), and such a concept may be transferred to a landscape of different forest types or habitats, including shrublands. Landscape may be discussed as a set of values ordered within a view (CAUQUELIN, 2008), where the local ecosystems or land uses are repeated in similar form throughout, and mosaic stability, which includes analysis of land-use changes, is a key element of sustainable development and analysis.
Recent studies clarify the extent that land-use/cover change is the result, and a cause, of interaction between human societies and the environment (VALBUENA et al., 2010; VERBURG et al., 2010). The concept of landscape functions prevails, defined as the capacity or potential of landscapes to provide services such as food and fiber, regulation of environmental quality, as well as aesthetic qualities (BOLLIGER and KIENAST, 2010) and historical and future land-use and land-cover change have to be taken into account, namely landscape structure and composition.
Forest planning and landscape ecology
Forest planning is merged in these days with landscape ecology, a science provided for the marriage of geography and biology (ZONNEVELD, 1990) and the act of sustainable planning and design is defined as a heuristic process (LEITÃO and AHERN, 2002).Twentieth century management activities have significantly influenced forest landscapes, and altered spatial patterns of physiognomies, cover types and structural conditions. In southern Portugal ACACIO et al. (2009) concluded that cork oak forests have been decreasing since 1985 along the time series 1958-2002, while Cistus shrublands have been the most persistent and expanding, correlated with wildfires. HOUET et al. (2010) conclude that projection of future landscape changes requires an understanding and integration of past landscape trends, current land change processes and feedbacks, and the incorporation of plausible assumptions or scenarios, where the temporal dimension of landscapes has to be considered in order to monitor, model and assess human/nature interactions.
Ecomosaic
Ecomosaic is a term defined as to be whole regions composed of landscapes and whole landscapes composed of local ecosystems with the focus on geomorphology, human culture and their interaction in producing the mosaics (FORMAN, 1995). NAGENDRA and GADGIL (1999) considered ecomosaics unities of observation at the scale of 108–1010 m2, inside ecoregions and composed by ecotopes; its basic features are composition, distribution and configuration of patches of different habitats - composition relies on number and proportions of patch types, while configuration is spatial and includes the arrangement of patches.
The composition of a mosaic is a fundamental indicator of patterns within the landscape (see O'NEILL et al., 1988; LI and REYNOLDS, 1994) and in land cover pattern assessment (RIITERS et al., 2009); pattern and process are assumed to be interactive and process creates, modifies and maintains pattern, whereas pattern constrains, promotes, or neutralizes processes (LI and WU, 2004). Ecological resilience is an important theme and there are systems with high variability and high resilience but low stability, as stability and resilience may have an inverse relationship (ALLEN et al., 2010a), but in general where management has reduced variability often means that ecologic shifts have greater negative impact.
Landscape changes and economic values
Environmental economists claim that monetary values are necessarily assigned to landscape, at least implicitly, by decisions involving landscape changes (VERBIC and SLABE-ERKE, 2009) with emphasis on cost-benefit analysis, contingent valuation and willingness-to-pay methods. In practice, forest planning deals with several frontiers of knowledge: economic preferences, ecologic constraints, constitutional rights and ethical demands. Economic preferences have its own driving impulse under stationary market forces and should be focused as a primer scenario generator.
Resilience may be lost because of management activities that focus on an optimal control strategy of a single target variable (ALLEN et al., 2010b). Landscape processes are nested in a spatio-temporal hierarchy (O'NEILL et al., 1989; GILLSON, 2009) and geomorphology and climate may influence landscape pattern and processes at many hierarchical levels (BAILEY, 2005) but at intermediate or lower levels land use is the most important factor that structures landscapes (DÍAZ-VARELA et al., 2009) and land-use change is affected by economic preferences as driving forces.
About two decades ago I emphasized reposition cost as an economic indicator concerning conservation of forest resources (CASQUILHO, 1994), as it points to the expected investment necessary to recover an existent forest habitat under a perspective of loss. Recently, the municipality of Nisa published a technical document under the scope of the national strategy for forests in Portugal, where reposition costs of different pure or mixed stands where estimated in euros per hectare - a total of 121 combinations of pure and mixed classes of eleven forest habitats and shrublands (see PMDFCIN, 2007), which include the main types I select for further developments in this paper: cork oak (Quercus suber); holm oak (Q. rotundifolia); eucalyptus plantations (Eucalyptus globulus); and pine groves of two kinds, maritime or cluster pine trees (Pinus pinaster) and stone pines(P. pinea). Table 1 summarizes the estimates of reposition costs in €/ha, where I designate such numbers with the symbol wi (meaning weight factor or characteristic value).
Table 1 – Estimates of reposition costs (wi: €/ha) of different forest habitats in the region of Nisa, extracted from PMDFCIN (2007); codes: qs-Quercus suber; qr- Quercus rotundifolia; eg- Eucalyptus globulus; pb- Pinus pinaster; pm- Pinus pinea
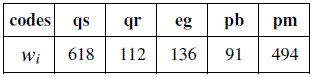
The problem that is discussed next in this paper may be stated as follows: given these estimates of economic value as reposition costs is there any conceptual device that generates compositional solutions of ecomosaics for the region of Nisa, with some rationale that meets criteria of expected utility formulation? Can these solutions be benchmarked with bonds concerning average economic value and landscape diversity?
Methods
Theories
The role of mathematical models, formulas, indices, is generating compromises of meaning-making such that the results are somewhat insightful, crossing the semantic level and providing clues for further research. O'HALLORAN (2008) reminds that mathematical discourse is multisemiotic: the grammar of mathematical symbolism is based on a range of condensatory strategies of meaning and the result is a semiotic resource which can be used as a tool for reasoning.
Decision theory relies on work of Daniel Bernoulli, with a corner stone in von Neumann work on theory of games in the forties, and can be stated as focused in (subjective) expected utility maximization (GILBOA, 2009), as a consumer may be typified like a von Neumann-Morgenstern utility maximiser (see BAUMOL, 1951), evaluating allocations and attaching subjective probabilities to events (ELLICKSON, 1993).
The expected-utility hypothesis has long being considered potentially rich in empirical content (see FRIEDMAN and SAVAGE, 1952) and makes operative the notions of maximum mean value of a set of states or events indexed by numbers. The normal form of mean or average utility is the calculation of the expected value of a preference pattern expressed by bounded numerical functions (BLACKWELL and GIRSHIK, 1979). It is believed that political or community decisions rely upon criteria that involve maximization of expected utility of some sort: subjective expected utility and discrete choice methods are a possibility and, in general, an operational characterization of states of a physical system leads to their description by a probability distribution. When an option's outcome is uncertain, expected utility analysis is performed according to multiple objectives and the decision space is multidimensional (WEIRICH, 2001). In the procedure that follows the decision space is outlined to be two dimensional, bonded to landscape diversity and average economic value, this one based on reposition costs of different forest habitats considered as characteristic values.
Indices W and Y
Assume that a system is characterized by a scenario of the world defined as the set of n elementary states, or index set, or sample space: 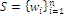 where
where 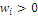 is a real number denoting a characteristic value of the elementary state indexed; the power set
is a real number denoting a characteristic value of the elementary state indexed; the power set 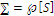 is the set of events, members of the collection generated by S; events – here defined as areas of different forest habitats - occur with probabilities linked to the distribution
is the set of events, members of the collection generated by S; events – here defined as areas of different forest habitats - occur with probabilities linked to the distribution 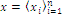 such that
such that 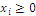 and
and 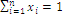 defining a
defining a 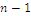 simplex; so the structure
simplex; so the structure 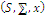 is a normalized measure space or probability space and we can write the set of references of the system:
is a normalized measure space or probability space and we can write the set of references of the system: 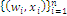 where the ordered pair
where the ordered pair 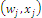 refers to habitat j in the context of the mosaic, represented by a characteristic value and a relative extension measure, with the condition
refers to habitat j in the context of the mosaic, represented by a characteristic value and a relative extension measure, with the condition 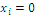 meaning absence of the indexed state.
meaning absence of the indexed state.
Index W is defined as a real positive number computed with the formula 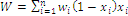 , an average value, or expected value, of a discrete random variable U that assumes utility values
, an average value, or expected value, of a discrete random variable U that assumes utility values 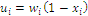 with probabilities
with probabilities 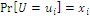 for
for 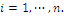 The number
The number 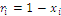 with
with 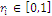 defines a measure of rarity or scarcity of the state or event indexed by
defines a measure of rarity or scarcity of the state or event indexed by 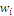 as it is the additive complement of the probability, with the set verifying the equation
as it is the additive complement of the probability, with the set verifying the equation 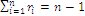 , the dimension of the simplex; we may consider the utility functions
, the dimension of the simplex; we may consider the utility functions 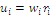 as a numeric approach to contributive values, as they combine in a product characteristic and context values, the last defined as a rarity measure. Contributive value is a relational form of value, it is the value that some part confers on the whole of which it is a part, because this contribution is conditioned by the other parts of the whole (STRATTON-LAKE, 2004).
as a numeric approach to contributive values, as they combine in a product characteristic and context values, the last defined as a rarity measure. Contributive value is a relational form of value, it is the value that some part confers on the whole of which it is a part, because this contribution is conditioned by the other parts of the whole (STRATTON-LAKE, 2004).
Whether the habitat tends to fulfill the area, its scarcity becomes null and also contributive value vanishes; the utilities 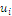 decrease in
decrease in 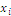 but increase with
but increase with 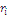 as
as 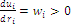 ; so, scarcity as a measure of the information value of a event is considered relevant. That valuation procedure goes with the general statement in information theory that the least a situation is probable the most significant it becomes (see PETITOT, 2004).
; so, scarcity as a measure of the information value of a event is considered relevant. That valuation procedure goes with the general statement in information theory that the least a situation is probable the most significant it becomes (see PETITOT, 2004).
Index W is thus generated as the expected value of a random utility pattern defined by real functions and is mathematically analogous to index 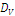 (CASQUILHO et al, 2003) and index V (CASQUILHO, 2009) with slight differences in notation, but quite distinct semantic blocking and interpretation.
(CASQUILHO et al, 2003) and index V (CASQUILHO, 2009) with slight differences in notation, but quite distinct semantic blocking and interpretation.
We may extend W index to a family of indices with a simple generalization of utility functions defined as a 1-parameter family 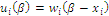 with
with 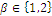 , keeping the domain as the
, keeping the domain as the 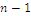 simplex and writing the index generator formula
simplex and writing the index generator formula 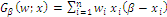 ; we get the obvious result
; we get the obvious result 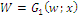 and also obtain
and also obtain 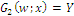 , with the formula for index Y written as
, with the formula for index Y written as 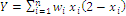 ; here the utility functions are defined as
; here the utility functions are defined as 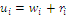 , a formula that enhances the presence of the characteristic value. In any case, arguments on convexity and differentiability ensure that there exists only an optimal solution, a point of maximum value, for any of the indices, given a fixed set S of characteristic values.
, a formula that enhances the presence of the characteristic value. In any case, arguments on convexity and differentiability ensure that there exists only an optimal solution, a point of maximum value, for any of the indices, given a fixed set S of characteristic values.
Results
Optimal points[2]
Optimal solution of index W, a point with n coordinates symbolised 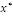 , may be found with an algorithmic procedure based on a Lagrange multiplier method. We may proceed with a bottom-up or top-down scheme, here I choose one of the last kind: compute
, may be found with an algorithmic procedure based on a Lagrange multiplier method. We may proceed with a bottom-up or top-down scheme, here I choose one of the last kind: compute 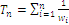 and discard the lowest characteristic value that verifies
and discard the lowest characteristic value that verifies 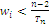 recalculating T without that number and recurring until we have verified
recalculating T without that number and recurring until we have verified 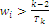 for all the (remaining) characteristic values of the habitats; then, the formula for the maximum point coordinates indexed by i is defined as:
for all the (remaining) characteristic values of the habitats; then, the formula for the maximum point coordinates indexed by i is defined as: 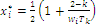 , where k is the cardinal of the subset of the original n variables that verify the inequality condition, and the other variables are set to zero; we obtain bounded solutions
, where k is the cardinal of the subset of the original n variables that verify the inequality condition, and the other variables are set to zero; we obtain bounded solutions 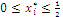 and the null coordinate(s) may exist only for
and the null coordinate(s) may exist only for 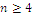 , hence we have a barrier
, hence we have a barrier 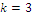 . Optimal coordinates don’t change if we change unities of the characteristic values by a linear transformation. Whenever the mosaic is reduced to a uniform matrix of a single habitat, calculating index W turns out the value zero, so denoting that there is a diversity measure attached in its mathematical structure: a germ of a related form of a measure of the concentration of the classification defined as λ (SIMPSON, 1949).
. Optimal coordinates don’t change if we change unities of the characteristic values by a linear transformation. Whenever the mosaic is reduced to a uniform matrix of a single habitat, calculating index W turns out the value zero, so denoting that there is a diversity measure attached in its mathematical structure: a germ of a related form of a measure of the concentration of the classification defined as λ (SIMPSON, 1949).
Optimal point for index Y exists as well, obtained with the same recursion procedure described for index W modified with the calculation formula for the coordinates of maximum point now defined as: 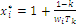 if
if 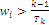 , otherwise the coordinates are settled to zero; unlike index W index Y has minimum value
, otherwise the coordinates are settled to zero; unlike index W index Y has minimum value 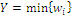 . For
. For 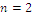 the optimal coordinates are
the optimal coordinates are 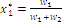 and
and 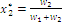 and we deduce the results
and we deduce the results 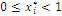 and that there is a barrier
and that there is a barrier 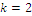 . The optimal point coordinates of index Y also don’t change when we change unities of the characteristic values by a linear transformation. Index Y is of the form of a value index, far enough from a diversity germ that entails and constrains index W.
. The optimal point coordinates of index Y also don’t change when we change unities of the characteristic values by a linear transformation. Index Y is of the form of a value index, far enough from a diversity germ that entails and constrains index W.
Compositional forest planning scenarios in the region of Nisa
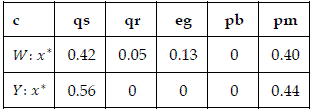
Let us admit that we have a large area suitable to ecomosaics concept where we could replicate indistinctly without biophysical constraints and property restrictions five different forest habitats of the region: those listed in Table 1 with codes {qs,qr,eg,pb,pm}. We search the optimal solution for indices W and Y according to previously discussed algorithms and procedures. Table 2 summarizes the results, the numbers being proportions of composition of the mosaic with the forest habitats encoded previously.
Table 2 - Optimal solutions (points) of the indices (see codes in Table 1)
Discussion
Using two extra standard measures to anchor and discuss the results of compositional scenarios shown by optimal solutions of indices W e Y, I choose average economic value 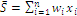 and landscape diversity calculated as Shannon entropy, considered an index sensitive to the presence of rare habitats and recommended for landscape management (NAGENDRA, 2002), defined with the standard formula
and landscape diversity calculated as Shannon entropy, considered an index sensitive to the presence of rare habitats and recommended for landscape management (NAGENDRA, 2002), defined with the standard formula 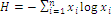 , log function being natural logarithms based and so the total sum is expressed in unities named nits, making an analogy with bits.
, log function being natural logarithms based and so the total sum is expressed in unities named nits, making an analogy with bits.
Obviously, maximum economic value of the global area would be reached with the whole area covered with cork oak trees, and the minimum economic value with the area filled with stands of maritime pine, in any case the landscape diversity would be null: 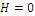 ; maximum landscape diversity is obtained with the indifference solution denoted
; maximum landscape diversity is obtained with the indifference solution denoted 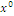 , meaning that each habitat fulfills 1/5 of the total area. Table 3 summarizes the numbers of these standard measures of the mosaic applied over three compositional scenarios.
, meaning that each habitat fulfills 1/5 of the total area. Table 3 summarizes the numbers of these standard measures of the mosaic applied over three compositional scenarios.
Table 3 - Measures of the mosaic - mean economic value 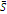 and landscape diversity H-, for three scenarios of composition: the optimal solution
and landscape diversity H-, for three scenarios of composition: the optimal solution 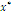 of indices W and Y and the indifference solution
of indices W and Y and the indifference solution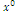 .
.

Utility analyses have been used in the policy design studies to help articulate conflicting preferences, to provide objective functions for the optimization efforts, and to simplify comparisons of policies (CLARK et al., 1979) and insight of simple models have direct application for management complex resource models under the concept of adaptive resource management. In general, GUNDERSON et al.(2010) say that system states and alternative domains exist at specific scale ranges, and those system states are comprised of entities with a characteristic set of attributes, remarking that multi-stable behavior can be explained by the use of models that include at least three but not more than five variables.
The reasoning described in this paper places indices W and Y as heuristic tools, that may be interpreted as expected utilities and generate compositional scenarios of the mosaic. I should say that the results from the example of planning scenario in Nisa show that index W seems to perform a better compromise concerning the tradeoff between landscape diversity and economic value than index Y - this one is quite radical promoting the habitats with high reposition costs and penalizing substantially landscape diversity.
Similar, but smoother, indices based on Shannon entropy generalizations also exist, and share the same principle of expected utility and information average values, as is the case with mean contributive value index (CASQUILHO, 2010). RICOTTA (2002) discuss Shannon based formulas under the hypothesis of bridging the gap between ecological diversity indices and measures of biodiversity. In any case we are faced with compromises concerning planning the composition of a large area with different forest types and the trade-off between two contexts: economic and ecologic, with their multiple interferences.
The axiomatic foundation of this compositional scenario generator method denoted 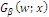 may be thought as rooted in two theories: situation theory, which is a theory of information and its key insight is that much information is always available and is representable only partially (PARIKH and CLARK, 2007) and relevance theory that entails that human cognition tends to be geared to the maximization of relevance (CANN et al., 2009), where relevance is defined as a trade-off between the effort needed to process some input and the informational benefit gained. The whole reasoning that was presented here may be conceived in terms of forest planning as a kind of abductive procedure entailing heuristic processes, noting that while deduction proves that something must be, and induction shows that something is actually operative, abduction - a term coined by C. S. Peirce -, merely suggests that something may be so (MOURÃO, 2007) - somewhere starting from an interaction between a human inquirer and its environment as a part of an interrogative process (PAAVOLA, 2007).
may be thought as rooted in two theories: situation theory, which is a theory of information and its key insight is that much information is always available and is representable only partially (PARIKH and CLARK, 2007) and relevance theory that entails that human cognition tends to be geared to the maximization of relevance (CANN et al., 2009), where relevance is defined as a trade-off between the effort needed to process some input and the informational benefit gained. The whole reasoning that was presented here may be conceived in terms of forest planning as a kind of abductive procedure entailing heuristic processes, noting that while deduction proves that something must be, and induction shows that something is actually operative, abduction - a term coined by C. S. Peirce -, merely suggests that something may be so (MOURÃO, 2007) - somewhere starting from an interaction between a human inquirer and its environment as a part of an interrogative process (PAAVOLA, 2007).
References
ACÁCIO, V., HOLMGREN, M., REGO, F, MOREIRA, F., MOHREN, G.M.J. 2009. Are drought and wildfires turning Mediterranean cork oak forests into persistent shrublands? Agroforestry Systems 76: 389-400 [ Links ]
ALLEN, C.R., GUNDERSON, L.H., HOLLING, C.S., 2010a. Commentary on part one articles. In Foundations of Ecological Resilience (GUNDERSON, L.H., ALLEN, C.R., HOLLING, C.S. eds). Island Press, Washington DC, pp. 3-18. [ Links ]
ALLEN, C.R., GUNDERSON, L.H., HOLLING, C.S., 2010b. Commentary on part three articles. In Foundations of Ecological Resilience (GUNDERSON, L.H., ALLEN, C.R., HOLLING, C.S. eds). Island Press, Washington DC, pp. 301-307. [ Links ]
ALVES, A.A.M, 1982. Técnicas de Produção Florestal, Instituto Nacional de Investigação Científica, Lisboa, 334 pp. [ Links ]
BAILEY, R.G., 2005. Identifying ecoregion boundaries. Environ. Management 34: 14-28. [ Links ]
BAUMOL, W.J., 1951. The Neumann-Morgenstern utility index-an ordinalist view. The Journal of Political Economy 59(1): 61-66. [ Links ]
BOLLIGER, J., KIENAST, F., 2010. Landscape functions in a changing environment. Landscape Online 21: 1-5. [ Links ]
BLACKWELL, D., GIRSHIK, M.A., 1979. Theory of Games and Statistical Decisions. Dover Publications Inc, New York, 355 pp. [ Links ]
CANN, R., KEMPSON, R., GREGOROMI-CHELAKI, E., 2009. Semantics - an Introduction to Meaning in Language. Cambridge University Press, New York, 292 pp. [ Links ]
CASQUILHO, J., 1994. Ecologia, modelos e impactes: critérios para uma ética do uso agroflorestal do solo. Revista Florestal7: 3-20. [ Links ]
CASQUILHO, J., 1999. Ecomosaico: Indices para o Diagnóstico de Proporções de Composição. (tese de doutoramento). Instituto Superior de Agronomia, Universidade Técnica de Lisboa, 205 pp. [ Links ]
CASQUILHO, J., NEVES, M., REGO, F., 2003. A generalisation of Simpson’s index of diversity. Technical Report #7/IISA, 3 pp. Universidade Técnica de Lisboa.
CASQUILHO, J.P, 2009. Complex number valuation of habitats and information index of the landscape mosaic. Silva Lusitana 17(2): 171-180. [ Links ]
CASQUILHO, J.P, 2010. Landscape mosaic composition and mean contributive value index. Silva Lusitana 18(2): 197-203. [ Links ]
CAUQUELIN, A., 2008. A Invenção da Paisagem (2ª ed.), Edições 70, Lisboa, 147 pp. [ Links ]
CLARK, W.C., JONES, D.D., HOLLING, C.S., 1979. Lessons for ecological policy design: a case study of ecosystem management. Ecological Modelling 7: 1-53. [ Links ]
DÍAZ-VARELA, E., ÁLVAREZ-LOPEZ, C.J., MAREY-PÉREZ, M.F., 2009. Multiscale delineation of landscape planning units based on spatial variation on land-use patterns in Galicia, NW Spain. Landscape Ecol. Eng. 5: 1-10. [ Links ]
ELLICKON, B., 1993. Competitive Equilibrium – Theory and Applications. Cambridge University Press, Cambridge, 394 pp. [ Links ]
FRIEDMAN, M., SAVAGE, L.J., 1952. The expected-utility hypothesis and the measurability of utility. The Journal of Political Economy 60(6): 463-474. [ Links ]
FORMAN, R.T.T., 1995. Land Mosaics – the Ecology of Landscapes and Regions. Cambridge University Press, Cambridge, 632 pp. [ Links ]
GILBOA, I., 2009. Theory of Decision under Uncertainty. Cambridge University Press, New York, 214 pp. [ Links ]
GILLSON, L., 2009. Landscapes in time and space. Landscape Ecology 24: 149–155. [ Links ]
GONÇALVES, A.C., OLIVEIRA, A.C., DIAS, S.S., 2010. Evolution in multi-species high forest stands in serra da Lousã: diversity analysis. Silva Lusitana nº especial: 79-90. [ Links ]
GUNDERSON, L.H., HOLLING, C.S., ALLEN, C.R., 2010. Conclusion: the evolution of an idea – the past, present, and future of ecological resilience. In Foundations of Ecological Resilience (GUNDERSON, L.H., ALLEN, C.R., HOLLING, C.S., eds) Island Press, Washington DC, pp. 423-444. [ Links ]
HOGANSON, H., BIXBY, J., BERGMANN, S., BORGES, J.G., 2004. Large-scale planning address interior space production: three case studies from Northern Minnesota. Silva Lus., vol.12, no.Especial, pp. 35-47. [ Links ]
HOUET, T., VERBURG, P.H., LOVELAND, T.R., 2010. Monitoring and modeling landscape dynamics. Landscape Ecology 25: 163–167. [ Links ]
LEITÃO, A.B., AHERN, J., 2002. Applying landscape ecological concepts and metrics in sustainable landscape planning. Landscape and Urban Planning 59: 65-93. [ Links ]
LI, H., REYNOLDS, J.F., 1994. A simulation experiment to quantify spatial heterogeneity in categorical maps. Ecology 75: 2446-2455. [ Links ]
LI, H., WU, J., 2004. Use and misuse of landscape indices. Landscape Ecology 19: 389–399. [ Links ]
MOURÃO, J.A., 2007. Abduction and metaphor. Tropism of truth. In Abduction and the Process of Scientific Discovery (POMBO, O. and GERNER, A. eds), Centro de Filosofia das Ciências da Universidade de Lisboa, Lisboa, pp. 265-281. [ Links ]
NAGENDRA, H., GADGIL, M., 1999. Biodiversity assessment at multiple scales: linking remotely sensed data with field information. Proc. Natl. Acad. Sci. USA 96: 9154–9158. [ Links ]
NAGENDRA, H., 2002. Opposite trends in response for the Shannon and Simpson indices of landscape diversity. Applied Geograpy 22: 175-186. [ Links ]
O'HALLORAN, K., 2008. Mathematical Discourse - Language, Symbolism and Visual Images. Continuum, London, 226 pp. [ Links ]
O'NEILL, R.V., KRUMMEL, J.R., GARDNER, R.H., SUGIHARA, G., JACKSON, B., DEANGELIS, D.L., MILNE, B.T., TURNER, M.G., ZYGMUNT, B., CHRISTENSEN, S.W., DALE, V.H., GRAHAM, R.L., 1988. Indices of landscape pattern. Landscape Ecology 1: 153-162. [ Links ]
O'NEILL, R.V., JOHNSON, A.R., KING, A.W., 1989. A hierarchical framework for the analysis of scale. Landscape Ecology 3 (3/4): 193-205. [ Links ]
PAAVOLA, S, 2007. Abductive logic of discovery with distributed means. In Abduction and the Process of Scientific Discovery (POMBO, O. and GERNER, A. eds), Centro de Filosofia das Ciências da Universidade de Lisboa, Lisboa, pp. 47-62. [ Links ]
PARIKH, P., CLARK, R., 2007. An introduction to equilibrium semantics for natural language. In Game Theory and Linguistic Meaning (Pietarinen, A-H. ed). Elsevier Ltd., Oxford, pp. 149-158. [ Links ]
PEARCE, D.W., 2001. The economic value of forest ecosystems. Ecosystem Health 7(4): 284-296. [ Links ]
PEARCE, D. W., PEARCE, C.G.T., 2001. The Value of Forest Ecosystems. Secretariat of the Convention on Biological Diversity. CBD Technical Series 4: 1-67, Montreal. [ Links ]
PMDFCIN, 2007. Plano Municipal de Defesa da Floresta Contra Incêndio de Nisa. Câmara Municipal de Nisa e Florasul, 327 pp. [ Links ]
PETITOT, J., 2004. Morphologie et Esthétique. Maisonneuve & Larose, Paris, 374 pp. [ Links ]
RICOTTA, C., 2002. Bridging the gap between ecological diversity indices and measures of biodiversity with Shannon's entropy: comment to Izsák and Papp. Ecological Modelling 152(1): 1-3. [ Links ]
RIITTERS, K.H., WICKHAM, J.D., WADE, T.G., 2009. An indicator of forest dynamics using a shifting landscape mosaic. Ecological Indicators 9: 107-117. [ Links ]
SIMPSON, E.H., 1949. Measurement of diversity. Nature: 163: 688. [ Links ]
STRATTON-LAKE, P., 2004.Kant, Duty, and Moral Worth. Routledge, New York, 157 p. [ Links ]
VALBUENA, D, VERBURG, PH, BREGT, A.K., LIGTENBERG, A., 2010. An agent-based approach to model land-use change at a regional scale. Landscape Ecology 25: 185–199. [ Links ]
VERBIČ, M., SLABE-ERKER, R., 2009. An econometric analysis of willingness-to-pay for sustainable development: a case study of the Volčji Potok landscape area. Ecological Economics 68(5): 1316-1328. [ Links ]
VERBURG, P., van BERKEL, D., van DOORN, A., van EUPEN, M. and van den HEILIGENBERG, H., 2010. Trajectories of land use change in Europe: a model-based exploration of rural futures. Landscape Ecology 25: 217-232. [ Links ]
WEIRICH, P., 2001. Decision Space: Multidimensional Utility Analysis. Cambridge University Press, Cambridge, 272 pp. [ Links ]
ZONNEVELD, I., 1990. Scope and concepts of landscape ecology as an emerging science. In Changing Landscapes: an Ecological Perspective (ZONNEVELD, I., FORMAN, R.T.T. eds.), Springer-Verlag, New York, pp. 1-20. [ Links ]
Acknowledgments
Eng. Carlos Janeiro, from the municipality of Nisa, for providing the technical document quoted: PMDFCIN (2007).
Entregue para publicação em Janeiro de 2011
Aceite para publicação em Maio de 2011
Notas
[1] Translated into English from the original: GOMES, A.M.A., 1985. Uma Alternativa Sectorial. Publicação Ciência e Vida Lda. Lisboa, p. 37
[2] Mathematical proofs of the results are available in CASQUILHO (1999).













