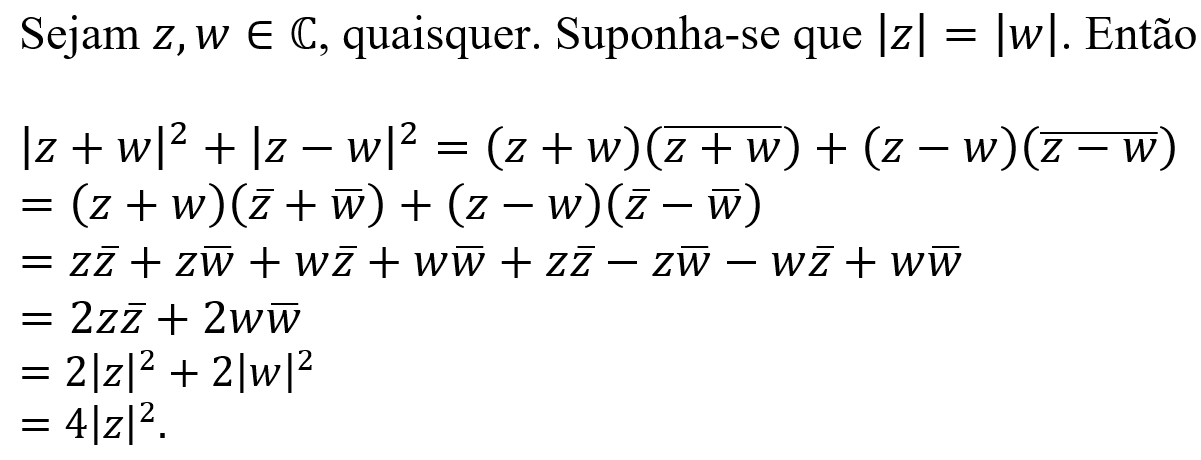1. INTRODUÇÃO
Informar é a tendência da investigação sobre erros cometidos por estudantes no processo de ensino-aprendizagem em matemática, pois, segundo Gris et al. (2019), são poucos os estudos que concretizam formas de lidar com esses erros. Algumas propostas recentes que visam a atividade, motivadora e provocadora, de explicar e dar sentido aos erros (Rico, 1995; Pinto, 1998) são: aprendizagem pelos pares, considerando os erros na construção e na discussão de questões conceptuais (Peel et al., 2021); deteção e correção fundamentadas de exemplos erróneos pelo estudante (Rushton, 2018).
As referidas propostas inserem-se na temática do aproveitamento didático dos erros (Cury, 2007) - erros para o ensino -, para além dos erros para a investigação em que o professor pode ser investigador da sua sala de aula (Ponte, 2008). Apesar do interesse na análise e na classificação dos erros dos estudantes (Pinheiro et al., 2008), o propósito principal é o desenvolvimento de “estratégias de ensino que possam auxiliá-los em suas dificuldades” (Cury, 2007, p. 50) ou de “intervenções didáticas que desestabilizem as certezas, levando o estudante a um questionamento” (Pinto, 1998, p. 80). No sentido da desterritorialização e reterritorialização descritas por Deleuze e Guattari (2011a; 2011b), “o papel do professor consiste em desterritorializar didaticamente o erro, criando estratégias didáticas a partir do erro, para promover a aprendizagem” (Peel et al., 2021, p. 37) que implica uma consequente reterritorialização do erro.
Com vista ao referido aproveitamento didático, uma vez que a criação de tarefas e a colocação em prática de estratégias são elementos centrais da gestão curricular do professor (Ponte, 2005), pode pensar-se no desenho de tarefas baseado em erros. No presente trabalho, atendendo aos conceitos matemáticos (do tópico “números complexos”) a avaliar numa tarefa de demonstração incluída num momento de avaliação individual, pretende-se classificar os erros associados nas produções de estudantes do ensino universitário para essa tarefa. A partir dos erros identificados, relacionados com consequências da definição de módulo de um número complexo e com estratégias de demonstração em matemática, pretende-se construir recursos sob a forma de tarefas para a sala de aula: questões conceptuais; exemplos erróneos; tarefas de completamento; tarefas de modificação do enunciado.
Atendendo aos objetivos descritos, procuramos responder às seguintes questões de investigação: (1) quais os erros, relacionados com consequências da definição de módulo de um número complexo e com estratégias de demonstração em matemática, cometidos pelos estudantes nessas produções? (2) que tarefas podem ser construídas com base nesses erros? Para as tarefas construídas, produzindo uma linha de fuga que pode servir de base para uma verdadeira aprendizagem, tecemos considerações úteis para a prática de professores dos ensinos pré-universitário e universitário no que se refere a números complexos. Salientamos, ainda, que as tarefas construídas podem ser relevantes para a realização de estudos de aula e em engenharia didática, em que as tarefas têm um papel central, e como referem Watson e Ohtani (2015), “task design is at the heart of effective teaching and learning of mathematics” (p. vi).
2. ENQUADRAMENTO TEÓRICO
2.1. O ERRO NO PROCESSO DE ENSINO-APRENDIZAGEM
Comenius, considerado pai da Didática, acreditava que existia um método único para ensinar qualquer coisa de qualquer área, tendo idealizado uma única metodologia para resolver os problemas que envolvem a aprendizagem. Mas até hoje, de facto, não conseguimos entender como é que a aprendizagem ocorre em todos os seus passos e em todos os sujeitos, para que pudéssemos construir um método de ensino que conseguisse efetivar a aprendizagem na totalidade dos estudantes e na totalidade das áreas.
Muitos estudantes carregam por todo o processo escolar problemas com a aprendizagem da matemática, chegando ao nível superior com dificuldades que incidem em erros nas respostas às tarefas propostas, revelando uma incompreensão dos conceitos e dos objetos estudados. Neste trabalho, propomo-nos a pensar no erro e no desenho de tarefas como uma hipótese viável para que a aprendizagem aconteça em matemática, mas sempre por meio de agenciamentos e experimentações.
Segundo Cury (2007) e Torre (2007), os erros são recorrentemente subestimados e pouco considerados, sendo muitas vezes identificados somente nas avaliações e usados para uma classificação dos estudantes em aprovados e reprovados, sendo que, em inúmeras vezes e na maioria das situações, não há uma análise desses erros pelos professores e nem pelos estudantes. Os autores citados, bem como Pinto (1998) e Peel et al. (2021), defendem que os erros podem ser melhor utilizados se adotarmos uma nova postura diante deles, entendendo-os como parte do processo de aquisição do saber, com potencial construtivo e criativo; é urgente, então, estabelecer uma linha de fuga desse território conceitual e desse posicionamento tradicional.
Por isso, é importante pensar numa desterritorialização do conceito de erro, como proposto por Peel et al. (2021), induzindo um deslocamento que parte da ocultação para a centralização no processo de ensino e de aprendizagem; devemos, assim, pensá-lo no movimento entre o não aprender e o aprender, implicando uma consequente reterritorialização. Pensar no erro é pensar no movimento, no acontecimento. Num modo cartográfico, Iafelice (2015) afirma que:
Todo aprender está sempre em um “entre”, ou seja, o aprender está bem no meio entre o não saber e o saber. Dessa forma, todo aprendizado é uma passagem, uma variação de estados que gira em torno de algo ainda não conhecido para algo conhecido. (p. 34)
Os conceitos de territorialização, desterritorialização e reterritorialização que aqui utilizamos advêm da filosofia de Deleuze e Guattari (2011a; 2011b), sendo compreendidos como “lugares de passagem”, que são atravessados por multiplicidades, por encontros, por agenciamentos, por ritornelos e por linhas de fuga. E, em relação ao ensino, torna-se necessária a mudança de hábitos e de ritmos quando pensamos na aprendizagem efetiva, conforme Guattari e Rolnik (1996) definem:
O território pode se desterritorializar, isto é, abrir-se, engajar-se em linhas de fuga e até sair do seu curso e se destruir. A espécie humana está mergulhada num imenso movimento de desterritorialização, no sentido de que seus territórios “originais” se desfazem ininterruptamente [...]. (p. 323)
Novos lugares, novos olhares, novos hábitos e novos conceitos são necessários para uma aprendizagem que considere o erro como passagem e como movimento. Neste sentido, as ações feitas coletivamente por professores e por estudantes, na multiplicidade, poderão criar a partir do erro, elaborando por meio de experimentações, mapeando o saber. Por esse caráter relacional do processo de desterritorialização e reterritorialização, concordamos com Deleuze e Guattari (2011a) no sentido que
Jamais nos desterritorializamos sozinhos, mas no mínimo com dois termos [...]. E cada um dos dois termos se reterritorializa sobre o outro. De forma que não se deve confundir a reterritorialização com o retorno a uma territorialidade primitiva ou mais antiga: ela implica necessariamente um conjunto de artifícios pelos quais um elemento, ele mesmo desterritorializado, serve de territorialidade nova ao outro que também perdeu a sua. Daí todo um sistema de reterritorializações horizontais e complementares. (p. 41)
É preciso, então, que consigamos criar encontros e agenciamentos como dispositivos que permitam experimentações autênticas, que, por sua vez, trarão acertos e erros como atividades, igualmente autênticas, com emoções e percepções - parte importante do processo de individuação calcado em singularidades profícuas; ora, somente singularidades desse tipo é que permitirão que os erros, enquanto desvios, sejam úteis como errâncias entre territórios. Sem emoções, sem percepções e sem atividades legítimas, as experimentações não o serão em sua autenticidade, estabelecendo-se apenas como entretenimento ou ocupação: os afetos seguem as percepções apenas quando há realmente agenciamento afetivo e ativo.
Deleuze (2000), com quem concordamos, assegura que a aprendizagem acontece por meio da decifração de signos, por intermédio dos signos, nos agenciamentos, na imanência do encontro, com o que concordam também Oliveira et al. (2019). A análise do erro como um método de ensino pode ser uma linha de fuga para a desterritorialização do erro, promovendo a aprendizagem que aumenta a potência de agir e existir dos sujeitos em suas manifestações científicas, sociais e políticas.
Assim, por meio do movimento, dos agenciamentos, das novas relações com o objeto sígnico, dos encontros com os pares e com os professores, o erro torna-se uma fonte para a aprendizagem. Mais concretamente, o erro, ao tornar-se observável (tomada de consciência do erro) e superável (por meio do desequilíbrio das estruturas mentais) para os estudantes (Pinto, 1998), age como um dispositivo, como um operador do devir aprendizagem.
2.2. UM CASO PARTICULAR DA IDENTIDADE DO PARALELOGRAMO
Seja V um espaço vetorial real ou complexo, de dimensão finita, com produto interno .,. . Consideremos a norma . induzida por .,. , isto é, . = .,. . Em 𝑉 é válida a chamada identidade do paralelogramo:
‖u+v‖^2+‖u-v‖^2=2‖u‖^2+2‖v‖^2.
Se ‖u‖=‖v‖, então obtém-se um caso particular desta identidade:
‖u+v‖^2+‖u-v‖^2=4‖u‖^2.
A validade da identidade do paralelogramo no corpo ℂ dos números complexos é consequência do mesmo poder ser definido como o conjunto ℝ 2 munido da adição usual e de uma multiplicação adequada (Beites, 2018), operações estas que conferem a estrutura algébrica de espaço vetorial real a ℝ 2 . Esta identificação de ℂ com ℝ 2 é conhecida como construção algébrica dos números complexos, permitindo a definição construtiva destes (Beites, 2018).
Recorrendo à mencionada identificação, o módulo de um número complexo pode ser identificado com a norma de um vetor de ℝ 2 cujas coordenadas são a parte real e o coeficiente da parte imaginária do complexo. Neste sentido, a representação do referido caso particular da identidade do paralelogramo em ℂ é:
se z, w∈ℂ com z = w , então |z+w| 2 + |z−w| 2 =4 z 2 .
Para além da rápida, e elegante, demonstração proporcionada pela definição construtiva dos números complexos, é também possível provar o mencionado caso particular via definição descritiva dos números complexos (Fig. 1), ou seja,
C={a+bi:a,b ∈R∧i^2=-1}.
A aplicação de uma conhecida propriedade (para qualquer 𝑧∈ℂ, 𝑧 2 =𝑧 𝑧 ), utilizando o conceito de número complexo na sua forma mais abstrata - sem necessidade de escrever as suas partes real e imaginária -, providencia outra demonstração do referido caso particular da identidade do paralelogramo em ℂ (Figura 2).
Na Figura 3 e na Figura 4 apresentamos dois esboços de demonstrações que são variações lógicas das demonstrações, respetivamente, na Figura 1 e na Figura 2. Concretamente, são demonstrações por equivalência lógica e valor lógico verdade da última igualdade.
2.3. DESENHO DE TAREFAS A PARTIR DE ERROS
Segundo Ponte (2005), “Quando se está envolvido numa actividade, realiza-se uma certa tarefa. Uma tarefa é, assim, o objectivo da actividade.” (p. 11). As tarefas, por exemplo sob a forma de enunciados escritos, têm um papel central na aprendizagem, nomeadamente, no estudo de aula e na engenharia didática (Kieran et al., 2015). Apesar disso, os relatos de investigações raramente dão detalhe suficiente sobre as tarefas de modo a ser possível construir conhecimento que permita alargar o seu domínio de aplicação (Gris et al., 2019; Watson & Ohtani, 2015). O estudo de Beites et al. (2022), no qual são identificados os erros de estudantes do ensino superior numa tarefa de demonstração de um caso particular da identidade do paralelogramo no âmbito dos números complexos, é um desses casos. O contexto matemático focado neste estudo enquadra-se na situação identificada por Kieran et al. (2015) como sendo adequada ao desenho de tarefas com aproveitamento pedagógico dos erros dos estudantes: “A particular issue for task design is the teaching of concepts that are known to be difficult for students because prior knowledge is in conflict with what is to be learned.” (Kieran et al., 2015, p. 47), uma vez que o conjunto dos números complexos pode ser considerado uma extensão do conjunto dos números reais, ainda que várias propriedades válidas em ℝ não o sejam em ℂ. Os mesmos autores apresentam princípios de conceção de tarefas (Tabela 1). Estes emergem de um estudo empírico efetuado tendo em conta as dificuldades e erros dos estudantes, na aprendizagem dos números racionais, devido às conceções já adquiridas relativas a números naturais. O ponto de partida para a construção de uma tarefa com este sentido é a questão: “How to deal with an incompatibility between students’ initial theories and intended mathematical development that unavoidably will occur?” (Kieran et al., 2015, p. 48). Kieran e colegas (2015) consideram a sequência de tarefas desenhadas nesse estudo empírico útil, tanto para professores (no sentido da sua prática letiva) como para estudantes (no sentido da sua aprendizagem), e os princípios de desenho de tarefas, que daí resultaram, de ampla aplicação. Princípios que entendemos mostrarem-se adequados ao estudo aqui apresentado.
Tabela 1: Princípios de desenho de tarefas para mudanças conceptuais
| Princípios de desenho |
| P1 - Ter em consideração os conhecimentos prévios dos estudantes e as potenciais conceções prévias (explorar a literatura existente). |
| P2 - Facilitar a consciencialização dos estudantes para os seus pressupostos de base, através da criação de oportunidades de externalização das suas ideias, para as compararem com as ideias dos colegas e para refletir sobre elas. |
| P3 - Utilizar modelos e representações externas, conhecer o seu poder e as suas limitações. |
| P4 - Fomentar o raciocínio analógico que apoia a reestruturação conceptual. |
Nota. (Kieran et al., 2015).
A justificação da escolha, características, modos de implementação, mediação do professor, ambiente de aprendizagem das tarefas é essencial, embora ainda seja pouco divulgado pelos investigadores, o que tornou relevante o problema do desenho de tarefas (Watson & Ohtani, 2015). Este tem sido foco de investigação de vários autores; destas investigações interessam-nos aquelas em que as tarefas são construídas a partir de erros (e.g. Adams et al., 2014; McLaren et al., 2015; Peel et al., 2021; Rushton, 2018). Na literatura identificam-se tipos diferentes de tarefas construídas a partir de erros e que são consideradas promissoras na promoção da aprendizagem, a partir do tratamento didático do erro: questões conceptuais, onde estes podem surgir nas opções (Mazur, 1997); exemplos erróneos para identificação fundamentada do(s) erro(s) (Barros et al., 2016; Peel et al., 2021; Rushton, 2018); tarefas de modificação do enunciado de modo a torná-lo verdadeiro (Cury, 2007; Peel et al., 2021); tarefas de completamento de enunciados (Peel et al., 2021; Zhang et al., 2016).
Seguindo Mazur (1997), uma questão conceptual é uma questão de escolha múltipla que deve obedecer a alguns critérios: focar-se num só conceito; não se poder resolver imediatamente com cálculos; estar escrita de forma clara; ter dificuldade média; ter opções boas. Este tipo de tarefa é utilizado na aprendizagem pelos pares, criada no âmbito do ensino-aprendizagem de Física (Mazur, 1997), metodologia adequada a tarefas construídas a partir de erros. Nesta metodologia (Beites & Romano, 2014), o professor parte de aspetos difíceis da leitura e escrita das dúvidas suscitadas aos estudantes pela leitura de um tópico e resolução de um trabalho de casa associado, previamente solicitado aos estudantes, ou de propostas suas que considera pertinentes propondo uma questão conceptual (ou várias) cuja opção de resposta é votada individualmente. Segue-se uma discussão das respostas dos estudantes com os seus pares, sempre que a percentagem de respostas corretas esteja entre 35% e 70%, funcionando o professor como mediador. Após esta discussão, cada estudante volta a responder à questão, em mais um típico evento de votação, mantendo ou não a sua opção de resposta inicial. O processo, para cada questão conceptual, termina com a divulgação e explicação da opção correta pelo professor ou, eventualmente, por um estudante (Beites & Romano, 2014).
A proposta de Rushton (2018) passa pela introdução de exemplos erróneos, sob a forma de tarefas resolvidas em casa e nas aulas, com vista à deteção e à correção fundamentadas de erros pelos estudantes. No estudo emergem resultados relevantes: não se encontra uma diferença significativa, com e sem utilização de erros, nas classificações em avaliações de um conteúdo realizadas logo após o processo de ensino-aprendizagem desse conteúdo; há uma diferença significativa, com e sem utilização de erros, nas classificações em avaliações de um conteúdo realizadas não imediatamente após o processo de ensino-aprendizagem desse conteúdo. Neste último resultado, especificamente, as classificações mais elevadas em avaliações desse conteúdo registam-se com utilização de erros no processo de ensino-aprendizagem.
Apesar do ensino expositivo associado ao estudo de Rushton (2018), o mesmo contempla momentos de discussão nas aulas, nomeadamente despoletados pelos exemplos erróneos, em pequeno grupo e em grande grupo. Têm-se, assim, momentos que são sessões de discussão de dúvidas norteadas pela análise de erros (Cury, 2007), em que se cria a possibilidade de o professor ampliar os saberes sobre os erros e melhorar a sua prática letiva (Pinto, 1998). Em Cury (2007) encontra-se a sugestão de aproveitamento pedagógico do erro comum de somar frações somando, respetivamente, os numeradores e os denominadores das frações parcelas, propondo tarefas de modificação do enunciado e explorando as condições a alterar de modo a que certa proposição passe a ser verdadeira. Também em Lee (2011) e Peel et al. (2021) se encontra este tipo de tarefa ao solicitarem a alteração das opções incorretas de modo a obter proposições verdadeiras de todas as formas que ocorram ao estudante. Peel et al. (2021) apresentam também uma tarefa de completamento envolvendo o conceito de universo matemático.
3. METODOLOGIA
A investigação, de natureza qualitativa, decorreu numa unidade curricular da área científica de matemática. Integrante do plano de estudos do 1.º ano de uma licenciatura de uma universidade portuguesa, o seu programa inclui números complexos como revisão. Com efeito, os estudantes conheciam os números complexos do ensino pré-universitário, segundo a definição descritiva, mas desconhecendo a definição construtiva que envolve a estrutura algébrica corpo.
Ao longo do semestre foram propostas tarefas envolvendo a elaboração de demonstrações, algumas relacionadas com números complexos. No presente trabalho consideramos a tarefa subsequente, suscetível de ser resolvida de várias formas, que constou de um momento de avaliação individual dos estudantes:
Sejam z, w∈ℂ. Mostre que se z = w , então |z+w| 2 + |z−w| 2 =4 z 2 .
A análise das produções dos 57 estudantes para esta tarefa foi realizada através de análise de conteúdo, “em torno de três polos cronológicos: a pré-análise; a exploração do material; o tratamento dos resultados, a inferência e a interpretação” (Bardin, 2016, p. 121). Apesar de Beites et al. (2022) terem apresentado uma classificação dos esquemas de demonstração e dos erros nessas produções, houve a necessidade de “reinventar os passos” (Cury, 2007, p. 61) no presente estudo.
O ponto de partida para a análise foram os conceitos matemáticos associados à avaliação com a tarefa: módulo de um número complexo; demonstração em matemática. A adequação da análise de conteúdo, reinventando os passos ao pretendido, pautou-se pelo seguinte objetivo final: desenho de tarefas baseado em erros, relacionados com consequências da definição de módulo de um número complexo e com estratégias de demonstração em matemática, nas produções para a tarefa supracitada.
Na pré-análise, tendo em conta o objetivo mencionado, escolhemos e organizámos o material recorrendo “a "leitura flutuante", em que o pesquisador” se deixa impregnar pelo material” (Cury, 2007, p. 63). Das 57 produções, descartámos: 12 produções em branco; 2 por conterem só (parte d)o enunciado, sem desenvolvimento; 1 produção correta. Assim, o corpus - conjunto das produções objeto de análise após a seleção realizada na pré-análise - é formado por 42 produções.
Na exploração do material, estudámos o corpus, definimos as unidades de análise (produções do corpus) e cada uma foi individualizada (unitarização) para proceder à categorização. A criação indutiva de (sub)categorias, com posterior aplicação dedutiva destas (Mayring, 2000), foi realizada por critérios estabelecidos ad hoc (Cury, 2007). A releitura do material, compreendendo o que há em comum, permitiu relacionar e reagrupar as unidades com vista à formação das (sub)categorias.
No tratamento de resultados, descrevemos cada categoria, e cada uma das subcategorias associadas a uma categoria, por meio de uma breve síntese sobre cada tipo de erro. Atendendo ao mencionado objetivo final, a inferência e a interpretação destes resultados não procuraram possíveis explicações para os erros identificados. Visam antes operacionalizar o desenho de tarefas, que são também resultados da investigação, com base nesses erros.
4. RESULTADOS
Na Tabela 2 apresentamos a contagem do número de ocorrências nas duas categorias de erros que criámos: ECMC - erros relacionados com a compreensão de consequências da definição de módulo de um número complexo; EEDM - erros relacionados com a compreensão de estratégias de demonstração em matemática.
4.1. RELATIVOS A ECMC
A categoria ECMC, dominante, é constituída pelos erros identificados que estão relacionados com a compreensão de consequências da definição de módulo de um número complexo, os quais foram organizados nas seguintes subcategorias (Tabela 3): (1) ECLM - erros relacionados com a aplicação das condições de linearidade à função módulo em C; (2) EIMC - erros relacionados com a igualdade de módulos de números complexos; (3) EEPR - erros relacionados com a extensão a C de propriedades da função módulo em R; (4) ECFM - erros relacionados com o contradomínio da função módulo em C.
Tabela 3: Distribuição dos erros por subcategorias da categoria ECMC
| Subcategoria | N.º de ocorrências |
| ECLM | 24 |
| EIMC | 24 |
| EEPR | 15 |
| ECFM | 5 |
| 68 |
Vinte e quatro (24) estudantes apresentam erros relacionados com a aplicação das condições de linearidade à função módulo em ℂ (subcategoria ECLM). A consequência da definição de módulo de um número complexo associada a esta subcategoria é a seguinte: a função módulo em ℂ não é linear. Desses estudantes: dezasseis (16) aplicam a primeira condição de linearidade de uma função; oito (8) aplicam as duas condições de linearidade de uma função.
Vinte e quatro (24) estudantes apresentam erros relacionados com a igualdade de módulos de números complexos (subcategoria EIMC). A consequência da definição de módulo de um número complexo associada a esta subcategoria é a seguinte: há complexos diferentes, com partes reais em módulo diferentes e com coeficientes das partes imaginárias em módulo diferentes, com o mesmo módulo. Desses estudantes: dezanove (19) deduzem o consequente 𝑧=𝑤 a partir da hipótese 𝑧 = 𝑤 ; três (3) consideram a hipótese 𝑧 = 𝑤 equivalente a 𝑧=𝑤; um (1) deduz 𝑤=−𝑧 a partir da hipótese 𝑧 = 𝑤 ; um (1) deduz o consequente 𝑅𝑒(𝑧) = 𝑅𝑒(𝑤) 𝑒 𝐼𝑚(𝑧) = 𝐼𝑚(𝑤) a partir da hipótese 𝑧 = 𝑤 .
Quinze (15) estudantes apresentam erros relacionados com a extensão a ℂ de propriedades da função módulo em ℝ (subcategoria EEPR). A consequência da definição de módulo de um número complexo associada a esta subcategoria é a seguinte: há propriedades da função módulo em ℝ que não são válidas em ℂ. Desses estudantes: doze (12) consideram que, para quaisquer 𝑧,𝑤∈ℂ, 𝑧 2 = 𝑧 2 ; dois (2) consideram que, para quaisquer 𝑧,𝑤∈ℂ, 𝑧 = 𝑤 ⟺𝑧 2 = 𝑤 2 ; um (1) considera que, para qualquer 𝑧∈ℂ, 𝑧 = 𝑧 2 .
Cinco (5) estudantes apresentam erros relacionados com o contradomínio da função módulo em ℂ (subcategoria ECFM). A consequência da definição de módulo de um número complexo associada a esta subcategoria é a seguinte: o contradomínio da função módulo em ℂ é ℝ 0 + . Desses estudantes: quatro (4) consideram que o módulo de um número complexo pode ser um número complexo não real; um (1) considera que o módulo de um número complexo é positivo, não contemplando a possibilidade do complexo nulo de módulo 0.
Na Figura 5 apresentamos uma questão conceptual com foco no conceito de módulo da adição de dois números complexos. Na sua construção, especificamente na alínea a), consideramos um tipo de erro da categoria ECMC, subcategoria ECLM. É fácil concluir que as opções b) e c) são incorretas, pois se 𝑧 2 =0 vem 𝑧 1 < 𝑧 1 e 𝑧 1 > 𝑧 1 , respetivamente, que constituem duas proposições falsas. Um contraexemplo para a) é obtido tomando 𝑧 1 =1 e 𝑧 2 =𝑖, o que conduz a 2 =2.
Na Figura 6 propomos um exemplo erróneo que inclui erros da categoria ECMC, subcategoria ECLM, observáveis pela aplicação das duas condições de linearidade à função módulo em ℂ. A proposta inclui ainda a aplicação, incorreta, da primeira condição de linearidade à função real de variável real dada por 𝑥↦ 𝑥 2 . Contudo, pode ser construído um exemplo erróneo que não contenha este último erro, ou seja, com o correto desenvolvimento dos quadrados da adição e da diferença de 𝑧 e 𝑤.
Na Figura 7 apresentamos uma questão conceptual focada no conceito de igualdade de módulos de números complexos. Na construção das alíneas a), b) e c), recorremos a todos os tipos de erros da subcategoria EIMC da categoria ECMC. A escolha da opção d) pode passar pela construção de contraexemplos para cada uma das alíneas precedentes ou de um contraexemplo que, em simultâneo, elimine as opções a), b) e c): 𝑧=1+2𝑖 e 𝑤=2+𝑖, ambos com módulo 5 .
Na Figura 8 consideramos o tipo de erro que corresponde à obtenção do consequente 𝑧=𝑤 a partir da hipótese 𝑧 = 𝑤 , pertencente à subcategoria EIMC da categoria ECMC, para construir um exemplo erróneo. De forma similar, é possível construir outro exemplo erróneo com o tipo de erro que corresponde ao consequente 𝑧=−𝑤 obtido a partir da hipótese 𝑧 = 𝑤 . Em cada exemplo erróneo, respetivamente, a segunda ou a primeira parcela da igualdade a provar é igual a 0.
A questão conceptual na Figura 9, focada no conceito de equivalência da igualdade dos módulos de dois números complexos, envolve erros da subcategoria EEPR da categoria ECMC (alíneas b) e c)). Também inclui, na alínea a), dois tipos de erros da subcategoria EIMC da categoria ECMC. As alíneas a) a c) constituem propriedades conhecidas no universo dos números reais, ideia que, aliada ao tipo de erro da subcategoria EEPR em b), levou à construção das tarefas na Figura 10, na Figura 11 e na Figura 12.
A tarefa de modificação de enunciado na Figura 10 tem múltiplas soluções. Uma alteração possível para a) a c) na Figura 9, relacionada com condições necessárias e suficientes, é 𝑧 = 𝑤 ⇐𝑧=𝑤. Uma vez que b) e c) envolvem multiplicação de números complexos, outra alteração possível para estas alíneas é 𝑧 = 𝑤 ⇔𝑧 𝑧 = 𝑤 𝑤. Alterações para a) a c) que também envolvam o universo matemático são, respetivamente: ∀𝑧∈ℝ, 𝑧 = 𝑤 ⇔𝑧=𝑤∨𝑧=−𝑤; ∀𝑧∈ℝ, 𝑧 = 𝑤 ⇔ 𝑧 2 = 𝑤 2 ; ∀𝑧∈ℝ, 𝑧 = 𝑤 ⇔ 𝑧 2 = 𝑤 2 .
As últimas propostas baseiam-se nos dois tipos de erro da subcategoria ECFM, da categoria ECMC. Na Figura 13, para além de um tipo de erro da subcategoria ECFM na alínea a) de uma questão conceptual, consideramos as formas algébrica e exponencial de um número complexo (alíneas a) e b)). Na alínea c) tomamos um tipo de erro da subcategoria EEPR. Na Figura 14 apresentamos outra questão conceptual cuja alínea a) inclui um tipo de erro desta subcategoria da categoria ECMC, não consideração do único número complexo de módulo 0.
4.2. RELATIVOS A EEDM
A categoria EEDM é constituída pelos erros relacionados com a compreensão de estratégias de demonstração em matemática, os quais foram organizados nas seguintes subcategorias (Tabela 4): ERLD - erros relacionados com raciocínio lógico-dedutivo; EREI - erros relacionados com raciocínio empírico-indutivo.
Tabela 4: Distribuição dos erros por subcategorias da categoria EEDM
| Subcategoria | N.º de ocorrências |
| ERLD | 10 |
| EREI | 2 |
| 12 |
Dez (10) estudantes apresentam erros relacionados com raciocínio lógico-dedutivo (subcategoria ERLD): seis (6) consideram outras formas da igualdade a provar sem escrever equivalências; dois (2) consideram a igualdade a provar como hipótese, sem ser estratégia de demonstração; um (1) considera uma combinação de duas estratégias de demonstração; um (1) não considera a hipótese 𝑧 = 𝑤 .
Dois (2) estudantes apresentam raciocínio empírico-indutivo sob a forma de um caso particular concreto (subcategoria EREI): um (1) considera dois números complexos concretos com o mesmo módulo; um (1) considera dois números complexos concretos que não possuem o mesmo módulo, sendo precisamente este o estudante, mencionado na subcategoria ERLD, que não considera a hipótese 𝑧 = 𝑤 .
Na Fig. 15 propomos uma tarefa que inclui um exemplo erróneo que contempla um tipo de erro da categoria EEDM, pertencente à subcategoria ERLD. A referida tarefa envolve, também, as duas estratégias de resolução com raciocínio lógico-dedutivo que foram exploradas na secção sobre um caso particular da identidade do paralelogramo. De forma análoga, pode ser construída uma tarefa similar com recurso à propriedade: para qualquer 𝑧∈ℂ, 𝑧 2 =𝑧 𝑧 .
Para a construção da tarefa de completamento na Figura 16 utilizamos um tipo de erro - não considerar a hipótese - da categoria EEDM, pertencente à subcategoria ERLD. Neste sentido, as duas alíneas na tarefa da Figura 16 pretendem, por um lado, promover o papel de hipótese numa proposição matemática e, por outro lado, proporcionar a visão de que o valor lógico da proposição incompleta dada depende da hipótese considerada.
Na Figura 17 propomos uma questão conceptual, focada no conceito de demonstração em matemática, tomando erros da categoria EEDM na construção das opções a) (subcategorias ERLD e EREI) e b) (subcategoria EREI). O tipo de erro em b) é também utilizado no exemplo erróneo da Figura 18. A opção d), apesar dos números complexos arbitrários, provém de não ser possível adicionar, e subtrair, números complexos na forma trigonométrica (ou exponencial) sem a possibilidade de os escrever na forma algébrica.
Na Figura 19, tendo em conta que o enunciado da tarefa associada ao presente estudo não o permitiria, procurámos criar uma situação com números complexos que ilustre que a validade de casos particulares não implica, necessariamente, a validade para quaisquer elementos do universo matemático considerado. Uma resolução poderia passar por concluir que, para quaisquer 𝑘, 𝑡∈ ℕ 0 , 𝑖 4𝑘+𝑡 = 𝑖 4 𝑘 𝑖 𝑡 =1 𝑖 𝑡 = 𝑖 𝑡 ∈ −1,0,−𝑖,𝑖 . Em alternativa, bastaria tomar, por exemplo, 𝑘=0 e 𝑡=1 em 𝑖 4𝑘+𝑡 , obtendo 𝑖.
5. DISCUSSÃO
Atendendo aos conceitos matemáticos associados à avaliação, a maioria dos erros identificados nas produções de estudantes para uma tarefa com números complexos é do tipo ECMC, relacionados com a compreensão de consequências da definição de módulo de um número complexo. A frequência desta categoria é cerca de seis vezes superior à da categoria EEDM, relativa aos erros de compreensão de estratégias de demonstração em matemática. A categoria dominante ECMC inclui os erros dominantes na totalidade das produções, que consistem na aplicação das condições de linearidade à função módulo em ℂ (ECLM) e estão relacionados com a igualdade de módulos de números complexos (EIMC). Estas subcategorias têm igual número de ocorrências e, em conjunto, constituem 70,6% dos erros da categoria dominante. O segundo tipo de erro mais frequente, também pertencente à categoria dominante, relaciona-se com a extensão a ℂ de propriedades da função módulo em ℝ (EEPR). Na categoria EEDM, não dominante, o erro mais frequente (83,3%) é relacionado com o raciocínio lógico-dedutivo (ERLD). Os tipos de erro com menor número de ocorrências registam-se numa subcategoria de cada categoria. Na categoria dominante (ECMC) dizem respeito a erros relacionados com o contradomínio da função módulo em ℂ (ECFM - 5 ocorrências); na categoria EEDM relacionam-se com o uso indevido de raciocínio empírico-dedutivo (EREI - 2 ocorrências).
A categorização descrita, a par da exploração da literatura realizada por Beites et al. (2022) na classificação dos esquemas de demonstração e dos erros nas produções dos estudantes, possibilitou a consideração dos conhecimentos prévios dos estudantes e das potenciais conceções prévias - princípio P1 de desenho de tarefas para mudanças conceptuais de Kieran et al. (2015). No sentido da criação de tarefas que permitem melhorar os processos de ensino-aprendizagem, como preconizam Gris et al. (2019), entendemos os erros como parte da aprendizagem, com potencial construtivo e criativo (Torre, 2007), estabelecendo uma linha de fuga por meio de uma desterritorialização do conceito de erro (Peel et al., 2021). Para além da noção de desterritorialização, tivemos também presentes os conceitos de territorialização e reterritorialização da filosofia de Deleuze e Guattari (2011a; 2011b), olhando o erro como passagem e como movimento para uma aprendizagem efetiva. Em particular, destaque-se o caráter relacional dos processos de desterritorialização e reterritorialização, sendo necessários encontros dos estudantes com os pares e com o professor. Este pode promover e conduzir discussões matemáticas (Ponte et al., 2013) com as tarefas construídas, em pequeno e em grande grupo, facilitando a consciencialização dos estudantes para os seus pressupostos de base, criando oportunidades de externalização, comparação e reflexão de ideias - princípio P2 de Kieran et al. (2015) - que podem desequilibrar as suas estruturas mentais (Pinto, 1998). Em particular, essa promoção está implícita em ambiente de aprendizagem pelos pares com as questões conceptuais construídas (Beites et al., 2022; Mazur, 1997), pela interferência do professor e de outros estudantes ao nível da Zona de Desenvolvimento Proximal de um estudante (Beites & Romano, 2014).
Procura-se ainda, embora numa perspetiva algo diferente, aplicar os princípios P3 - utilização de modelos e representações externas, conhecendo o seu poder e as suas limitações - e P4 - reestruturação conceptual suportada por raciocínio analógico - de Kieran et al. (2015). Estes autores procuram um modelo e uma representação externa - um elástico de borracha - para: evitar que a reta real continue a ser vista como uma régua com um número finito de pontos; construir uma analogia-ponte que permita a comparação, pelos estudantes, entre um objeto geométrico contínuo e a reta real. No presente estudo, encaramos os erros como modelos erróneos internos e representações erróneas internas dos estudantes, os quais são utilizados nas tarefas para proporcionar raciocínio analógico, eventualmente com erros, e discussões matemáticas (Ponte et al., 2013) que levem a uma reestruturação conceptual. Trata-se ainda de promover a monitorização meta-discursiva, prática não generalizada entre estudantes (Bagni, 2000) mas que os matemáticos utilizam, por exemplo, no contexto dos raciocínios analógico e indutivo quando, após compararem casos particulares e enunciarem uma conjetura, a vão testar e demonstrar se for verdadeira (Beites & Nicolás, 2016). Com a fundamentação explicitada, emergiram 15 tarefas de tipos diferentes (Tabela 5): 6 questões conceptuais seguindo Mazur (1997) e Peel et al. (2021); 6 exemplos erróneos para identificação fundamentada do(s) erro(s) seguindo Peel et al. (2021) e Rushton (2018); 1 tarefa de modificação do enunciado de modo a torná-lo verdadeiro seguindo Cury (2007) e Peel et al. (2021); e 2 tarefas de completamento seguindo Peel et al. (2021) e Zhang et al. (2016). Na Tabela 5, também se relaciona o tipo de tarefa criada com o tipo de erro utilizado no desenho da mesma.
Tabela 5: Distribuição das tarefas criadas por tipo e categoria de erro
| Tipo | Categoria | Total | ||
| ECMC | EEDM | |||
| Questão conceptual | 5 | 1 | 6 | |
| Exemplo erróneo | 3 | 3 | 6 | |
| Tarefa de modificação de enunciado | 1 | 0 | 1 | |
| Tarefa de completamento | 1 | 1 | 2 | |
| Total | 10 | 5 | 15 | |
Constata-se que a categoria de erros dominante, erros relacionados com a compreensão de consequências da definição de módulo de um número complexo (ECMC), possibilitou a criação de um maior número de tarefas e maior diversidade de tipos de tarefa que a categoria de erros relacionados com a compreensão de estratégias de demonstração em matemática (EEDM). A justificação prende-se com o facto de as subcategorias de ECMC serem 4 e as de EEDM serem 2 e de, dentro de cada uma, se distinguirem erros diferentes nas produções dos estudantes (respetivamente, 2 em ECLM, 4 em EIMC, 3 em EEPR, 2 em ECFM e 4 em ERLD e 2 em EREI), cada um dos quais possibilitando a construção de uma tarefa.
As questões conceptuais foram as criadas em maior número e tirando partido de erros relacionados com a compreensão de consequências da definição de módulo de um número complexo, focando: o conceito de módulo da adição de dois números complexos; o conceito de igualdade de módulos de números complexos; o conceito de equivalência da igualdade dos módulos de dois números complexos; as formas algébrica e exponencial de um número complexo; e a consideração do único número complexo de módulo 0. Estes aspetos foram utilizados para a elaboração das opções de resposta facultadas no enunciado.
A construção de exemplos erróneos foi efetuada em igual número, recorrendo a erros das duas categorias, e foi o tipo de tarefa construído em maior número com base nos erros da categoria não dominante (EEDM). Os exemplos erróneos foram construídos utilizando produções dos estudantes e solicitando a identificação e correção do(s) erro(s) neles existente(s). Além disso, é solicitado ao estudante que explique o(s) erro(s) e o que fez para obter uma resolução correta para a tarefa. Na formulação deste tipo de tarefas teve-se em conta os resultados estabelecidos em Rushton (2018), nomeadamente, que a explicação, por parte do estudante, da razão pela qual um raciocínio é correto ou incorreto fomenta a transferência de conhecimento e leva a melhores resultados de aprendizagem, do que, apenas, a explicação de soluções corretas, promovendo uma compreensão mais profunda do conteúdo e, portanto, retendo o estudante a informação por mais tempo.
As tarefas de modificação de enunciado e de completamento foram as construídas em menor número, não se tendo propiciado a construção de tarefas do primeiro tipo com base nos erros da categoria não dominante (EEDM). Estes tipos de tarefa são menos frequentes na matemática, mas apresentam potencial de aprendizagem elevado, pois são tarefas abertas com grau de desafio elevado (Ponte, 2005), ao exigirem do estudante a identificação do contexto matemático e das relações entre os conceitos envolvidos no enunciado. Em Peel et al. (2021) encontra-se um exemplo de cada uma, também no contexto dos números complexos, mas relativas ao desenvolvimento da expressão (𝑥+𝑦) 2 .
A única tarefa de modificação de enunciado construída tem por base uma questão conceptual, também proposta, e que usa erros das subcategorias EIMC e EEPR. É solicitado ao estudante que, fundamentadamente, altere, de todas as formas que lhe ocorram, as opções incorretas de modo a obter proposições verdadeiras.
Uma das tarefas de completamento solicita a indicação do universo matemático de modo a obter uma proposição ou verdadeira ou falsa, envolvendo uma propriedade válida em ℝ, mas não extensível a ℂ, erro frequente da categoria ECMC. A tarefa de completamento usando o erro da categoria EEDM, subcategoria ERLD, provém de o estudante não considerar a hipótese da proposição matemática dada na tarefa associada à investigação.
No presente estudo dão-se contributos para o erro ser uma estratégia didática inovadora (Pinto, 1998), tendo o erro de ser observável para o professor (primeiro passo) e observável para o aluno (segundo passo). Após a observabilidade do erro conseguida com a categorização de erros, para o segundo passo, também referido por Beites et al. (2020; 2022), o tratamento didático do erro prossegue com a construção de tarefas despoletada pela categorização. Em suma, criam-se oportunidades de promoção da aprendizagem do estudante, com tarefas que visam tornar o erro observável e superável para o estudante (Pinto, 1998), atuando o erro como um dispositivo ou operador do devir aprendizagem.
6. CONCLUSÕES
O tratamento didático do erro, de modo a promover a aprendizagem do estudante, exige ao professor reflexão e reformulações na sua prática letiva, dando lugar ao erro como passagem e como movimento entre o não aprender e o aprender.
O presente trabalho apresenta o desenho de tarefas à luz de princípios teóricos para mudanças conceptuais que partem de conceções e conhecimentos erróneos prévios dos estudantes, no sentido de facilitar a consciencialização destes, criando oportunidades de externalização das suas ideias, discussão com colegas e com o professor, e reflexão sobre elas.
As tarefas desenhadas, com potencialidade percetiva para mudança conceptual, visam tornar o erro observável e superável, o que as torna promissoras em promover a aprendizagem do estudante. Trata-se de proporcionar experimentações autênticas, que os estudantes vivenciem e que deem, por sua vez, origem a acertos e a erros como atividades, igualmente autênticas, com emoções e perceções.
Identificaram-se erros relacionados com a compreensão de consequências da definição de módulo de número complexo e de estratégias de demonstração em matemática. A partir destes foram criadas tarefas que se constituem como recursos didáticos relevantes, fundamentados e disponíveis para utilização por professores do ensino pré-universitário e do ensino universitário no que se refere a números complexos.
Salienta-se que se trata de um estudo que concretiza formas de lidar com os erros dos estudantes em números complexos, facultando tarefas de tipos diversificados: questões conceptuais; exemplos erróneos; tarefas de completamento; tarefas de modificação do enunciado. Estes tipos de tarefas são considerados, à luz da literatura, promissores na promoção da aprendizagem a partir do tratamento didático do erro.
A terminar, investigações futuras apontam para a implementação em sala de aula das tarefas criadas, explorando os ambientes de aprendizagem e as práticas pedagógicas mais adequados no sentido de promover aprendizagens nos estudantes.