INTRODUÇÃO
Segundo os Princípios e Normas para a Matemática Escolar (National Council of Teachers of Mathematics, 2007), as calculadoras e os computadores influenciam a maneira como a disciplina de Matemática é ensinada e melhoram a aprendizagem dos alunos. São dispositivos que possibilitam a visualização das ideias matemáticas, a organização e análise de dados, fazem cálculos de forma eficiente e exata e poderão servir de apoio a investigações dos alunos em qualquer área da Matemática.
De acordo com o NCTM, um dos requisitos importantes para um programa de Matemática de excelência, requer a integração da tecnologia, dado que a mesma favorece a aprendizagem e compreensão das ideias matemáticas, raciocinar matematicamente e comunicação de raciocínios (NCTM, 2017).
Neste artigo analisa-se a resolução de uma tarefa de Geometria de índole exploratória, com recurso ao artefacto mediador, calculadora gráfica.
Este estudo realizou-se no 7.º ano do ensino básico, numa escola pública do distrito de Setúbal, em Portugal, no ano letivo 2017/2018. Promoveu-se um ambiente de aprendizagem inovador, de natureza exploratória, com recurso à calculadora gráfica, Texas Instruments TI-Nspire, num nível de ensino em que não era prevista a utilização deste artefacto, de acordo com o currículo prescrito (Ministério da Educação e Ciência, 2013). No entanto, num estudo recente realizado pela primeira autora, a mesma concluiu que a realização de tarefas com a calculadora gráfica, no ensino básico, permite aos alunos raciocinar, refletir, aprender e compreender ideias matemáticas (Pedro, 2020).
Pretendemos analisar e compreender como é que a integração do artefacto mediador, calculadora gráfica, promoveu a construção de significados matemáticos na resolução de uma tarefa de Geometria.
As linhas teóricas que compõem os referenciais teóricos da Génese Instrumental e da Teoria da Mediação Semiótica sustentaram a análise dos dados. Neste contexto, temos como objetivos: 1) compreender como é que os esquemas de uso e os esquemas de ação instrumentada, mobilizados pelos alunos, contribuíram para o desenvolvimento do potencial semiótico do artefacto, calculadora gráfica e 2) na discussão coletiva, de que forma, a professora orientou a evolução de significados pessoais, relacionados com a tarefa e o artefacto, calculadora gráfica, para significados matemáticos.
ENQUADRAMENTO TEÓRICO
Artefacto
Um artefacto é um objeto usado como uma ferramenta, não sendo necessariamente físico (Drijvers et al., 2010), com a finalidade de realizar uma tarefa específica (Rabardel, 1995). A ideia de artefacto é muito geral e abrange vários tipos de objetos produzidos pelos seres humanos através dos tempos: sons e gestos, utensílios, formas de linguagem oral e escrita, textos, livros, instrumentos musicais, instrumentos científicos, ferramentas das tecnologias de informação e comunicação (Bussi & Mariotti, 2008).
O uso de um artefacto na resolução de uma tarefa matemática, pode proporcionar o emergir de conhecimento pré-existente do aluno, que se relaciona com o conhecimento matemático essencial à atividade de ensino e aprendizagem. O artefacto pode ser considerado como um gerador de conhecimento, onde se estabelece uma ligação entre a teoria e a prática (Mariotti, 2012).
Génese Instrumental - Esquemas de Uso e Esquemas de Ação Instrumentada
A Génese Instrumental designa-se pelo processo através do qual o sujeito se apropria de um artefacto ao perceber a sua utilidade no que respeita ao tipo de tarefas que pode fazer e à maneira como as pode realizar e o transforma num instrumento (Drijvers et al., 2010).
A construção de um instrumento não é espontânea, pois trata-se de uma entidade mista, onde se operacionaliza a apropriação de um artefacto, material ou simbólico, pelo sujeito, por meio de esquemas de utilização (Rabardel, 1995).
Rabardel (1995) descreve a noção de esquema de utilização de um artefacto como sendo um conjunto de procedimentos que organiza a atividade com o artefacto, associado à realização de uma determinada tarefa.
Para Drijvers e Trouche (2008), existe uma diferenciação entre dois tipos de esquemas de utilização: os esquemas de uso, direcionados para a gestão do artefacto e os esquemas de ação instrumentados, como esquemas mentais cujas ações são direcionadas para a realização da tarefa. Os esquemas mentais emergem de acordo com os significados pessoais do sujeito e podem ser espontâneos ou matemáticos.
Teoria da Mediação Semiótica - Potencial semiótico do artefacto e Ciclo Didático
A Teoria da Mediação Semiótica visa descrever e explicar o processo desencadeado por um aluno, que se inicia com o uso de um artefacto específico para realizar uma tarefa e o leva à apropriação de um conteúdo matemático específico (Mariotti & Maffia, 2018).
A Génese Instrumental pode ter um papel preponderante na realização de uma tarefa, na medida em que, quando o artefacto se transforma num instrumento, podem emergir signos associados aos esquemas de utilização (Mariotti, 2002).
A nível individual, podem surgir os signos de artefacto, que se referem à atividade realizada com o artefacto e normalmente são significados pessoais que estão relacionados com a experiência do sujeito. A nível social, podem surgir os signos matemáticos evocados, que se referem ao contexto da matemática e estão relacionados com os significados matemáticos partilhados na sala de aula. Estes signos constituem o objetivo do processo de mediação semiótica, orquestrada pela professora, na discussão coletiva. Neste sentido, o artefacto assume uma dupla relação semiótica, designada por potencial semiótico do artefacto, que se define pela capacidade que o mesmo possui em associar significados matemáticos evocados pelo seu uso, culturalmente determinados, com significados pessoais que cada sujeito desenvolve na utilização do mesmo (atividade instrumentada) na realização de tarefas específicas.
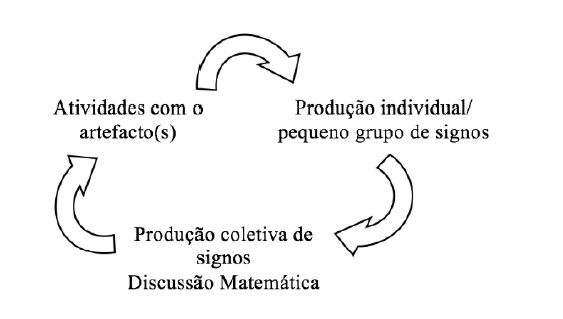
De acordo com a Teoria da Mediação Semiótica, o professor é o responsável pelo desenvolvimento do potencial semiótico do artefacto. Na discussão coletiva (discussão matemática) deve fomentar a produção de signos específicos e espontâneos pelos alunos (signos de artefacto), que estão associados ao uso do artefacto na realização da tarefa, como por exemplo, na realização de relatórios, orientando a evolução desses signos para os esperados signos matemáticos. Este processo, denominado por mediação semiótica, desenvolve-se através da iteração de Ciclos Didáticos (Figura 1) onde diferentes fases ocorrem:
Atividades com o artefacto - refere-se ao início de qualquer ciclo, onde se operacionaliza a realização de uma tarefa pelos alunos usando o artefacto com o objetivo de promover o emergir de signos (palavras, desenhos, gestos) cujos significados se referem ao uso do artefacto, sendo coerentes com os significados matemáticos que são o objetivo da intervenção didática. Atividades de produção individual de signos - é a fase onde os alunos se encontram envolvidos em atividades semióticas, isto é, em produções escritas em forma de relatórios individuais sobre atividades desenvolvidas com artefactos. Os alunos fazem uma reflexão, colocam dúvidas e questões e as suas produções escritas podem tornar-se objetos de discussão no trabalho coletivo subsequente.
Discussão coletiva - é a fase onde se promove a produção coletiva de signos. Toda a turma está envolvida: diversas soluções são discutidas coletivamente, os textos escritos pelos alunos ou outros são analisados, comentados e elaborados coletivamente. A orquestração do professor em torno das intervenções dos alunos visa promover o avanço para significados matemáticos. Desempenha um papel essencial no processo de ensino e aprendizagem e constitui o cerne do processo de mediação semiótica. Esta fase é realizada através de dois pares de Ações Complementares: “ação de retorno à tarefa e ação de focalização” e “solicitar uma síntese e oferecer uma síntese”. Na ação de retorno à tarefa, o professor pretende promover o maior número de contribuições dos alunos, no que respeita à produção de signos pessoais relacionados com o uso do artefacto. Na ação de focalização, o professor procura realçar signos pessoais (partilhados) até esse momento e selecionar aspetos pertinentes dos conceitos destes signos. Ao solicitar uma síntese, o professor objetiva promover a generalização e descontextualização dos signos pessoais que emergiram realizando a sua movimentação para signos matemáticos. Com o oferecer uma síntese, o professor tenciona tornar explícitas as relações entre significados matemáticos e os significados construídos através da discussão na sala de aula (Mariotti & Maffia, 2018).
METODOLOGIA
Este estudo está enquadrado numa investigação mais ampla, de natureza qualitativa, seguindo uma abordagem interpretativa e descritiva (Bogdan & Biklen, 1994). Adotou-se a modalidade estudo de caso, de modo a obter uma observação, compreensão, descrição minuciosa e dados mais consistentes. O estudo de caso incidiu no trabalho de dois pares de alunos, tendo sido adotados os nomes fictícios de Maria e Berta, para um grupo, e José Pedro para outro grupo (Creswell, 2012; Bogdan & Biklen, 1994).
A tarefa de índole exploratória incidiu no domínio da Geometria e foi realizada com o artefacto mediador, calculadora gráfica. Os objetivos focaram-se em 1) compreender como é que os esquemas de uso e esquemas de ação instrumentada, mobilizados pelos alunos, contribuíram para o desenvolvimento do potencial semiótico do artefacto, calculadora gráfica e 2) na discussão coletiva, de que forma a professora orientou a evolução de significados pessoais, relacionados com a tarefa e o artefacto, calculadora gráfica, para significados matemáticos.
A tarefa realizou-se em duas aulas consecutivas de 45 minutos. As mesmas ocorreram no ambiente natural da aula, numa turma do 7.º ano do ensino básico, com 29 alunos. Na primeira aula, os alunos foram informados que tinham de resolver a pares, a parte empírica da tarefa e realizar um relatório individual. Após a análise das produções individuais de cada aluno, na segunda aula, desenvolveu-se a discussão coletiva.
A análise dos dados centrou-se na análise dos registos realizados em gravações áudio, nas imagens das representações gráficas dos ecrãs da calculadora gráfica, nos relatórios escritos dos alunos e nas notas de campo registadas no diário de bordo. Foram observadas as normas relativas às questões éticas envolvidas em todo o processo de recolha e tratamento de dados (Creswell, 2012).
No que concerne às atividades com o artefacto e produção individual/pequeno grupo de signos, analisou-se como os alunos mobilizaram esquemas de uso e esquemas de ação instrumentada, desenvolvendo o potencial semiótico do artefacto, calculadora gráfica. Os alunos promoveram signos de artefacto, através do desenvolvimento de esquemas de uso e esquemas de ação instrumentada, na comunicação mobilizada entre os pares, com a professora e nos relatórios escritos.
No que respeita à produção coletiva de signos - discussão matemática, inerente à discussão coletiva, a análise dos dados focou-se na maneira como a professora promoveu a transição de signos de artefacto para signos matemáticos, de acordo com os dois pares de Ações Complementares, promovendo-se a construção do conhecimento matemático inerente ao objetivo didático da tarefa (Mariotti & Maffia, 2018).
A TAREFA APRESENTADA AOS ALUNOS
A tarefa (Figura 2) foi apresentada aos alunos no início da lecionação da unidade dos Quadriláteros, integrada no domínio da Geometria e Medida do 7.º ano de escolaridade (GM7). A mesma tinha como objetivo o reconhecimento que a soma das medidas das amplitudes dos ângulos internos de um triângulo é igual a um ângulo raso.
Na alínea a), para a construção da figura, era espectável que os alunos desenvolvessem os significados pessoais sobre o conceito de triângulo e retas paralelas.
Nas alíneas b) e c) procurou-se que os alunos verificassem a congruência entre o ângulo DBA e o ângulo A do triângulo [ABC], assim como a do ângulo CBE e o ângulo C do triângulo [ABC]. Deveriam usar os significados pessoais que tinham sobre ângulos alternos internos, isto é, dado que a reta AB era oblíqua às retas paralelas DB e AC, tinha-se A = D 𝐵 A e 𝐶 = C 𝐵 E. Neste sentido, a App de Geometria da calculadora gráfica seria utilizada para proceder à medição da amplitude dos ângulos e verificar a congruência dos mesmos. Posteriormente, os alunos deveriam de recorrer à ferramenta de arrastamento, movendo os vértices A ou B ou C do triângulo [ABC], de modo a confirmar que a igualdade se verificava para todos os triângulos representados.
Na alínea d) os alunos deveriam de mobilizar os significados pessoais sobre ângulos suplementares e ângulos rasos e através da calculadora gráfica proceder ao cálculo da soma das medidas dos ângulos DBA, ABC e CBE. Deveriam de confirmar que o resultado é sempre 180º, mesmo quando era utilizada a ferramenta de arrastamento, movendo os vértices A ou B ou C do triângulo [ABC]. Por outro lado, tendo em consideração a congruência dos ângulos que foi verificada nas alíneas b) e c), partindo das relações: 𝐴 = D 𝐵 A, 𝐵 = A 𝐵 C e 𝐶 = C 𝐵 E, deveriam de concluir através de linguagem simbólica, que 𝐴 + 𝐵 + 𝐶 = 180º, reconhecendo que a soma da medida das amplitudes dos ângulos internos de um triângulo é igual a um ângulo raso. Para confirmar esse procedimento analítico, deveriam de recorrer à calculadora gráfica e proceder à soma dos ângulos A, B e C, utilizando a ferramenta de arrastamento, movimentando os vértices A ou B ou C do triângulo [ABC], de modo a confirmar que a igualdade se verificava para outros triângulos, com diferentes dimensões.
APRESENTAÇÃO E ANÁLISE DOS RESULTADOS
1ª aula - Atividades com o artefacto e produção individual/pequeno grupo de signos
Relativamente à resolução da alínea a), surgiram os primeiros signos de artefacto. Os mesmos foram traduzidos no desenvolvimento de esquemas de ação instrumentada, quando emergiram significados pessoais que assentaram nos signos matemáticos inerentes ao conceito de triângulo e retas paralelas, aprendidos em anos letivos transatos. A operacionalização desses esquemas de ação instrumentada desencadeou a utilização de esquemas de uso, inerente à gestão do artefacto, calculadora gráfica:
1. Maria: E agora, como é que eu faço o triângulo? Vou a Geometria, menu, pontos e retas…
2. Berta: Não é nada pontos e retas, tens de ir a formas e depois triângulo, para desenhares o triângulo.
3. Maria: Já fiz o triângulo. E agora como fazemos a reta paralela? Já não me lembro de nada!
4. Berta: Pois eu também não! [Voltando-se para trás, a Berta questiona o colega]. José como é que vocês fazem a reta paralela?
5. José: Eu não acredito. A stora explicou! Porque é que não apontaram no caderno. Vão outra vez a menu, construção e paralela.
6. Pedro: Não se esqueçam de marcar os pontos D e E. Têm de ir a menu, pontos e retas e pontos sobre um objeto.
7. Maria: Stora, como faço para marcar os pontos A, B, C, D e E?
8. Professora: Vão a menu, ações e texto.
9. Maria: Já fiz! Que giro! Gosto disto!
A Maria mostrou-se uma certa dificuldade na manipulação e atribuição de sentido de algumas funções da calculadora gráfica. No entanto, a aluna manteve-se empenhada e conseguiu ser a primeira a construir o triângulo respeitante à alínea a).
Relativamente às alíneas b) e c), todos os alunos utilizaram esquemas de uso para proceder à medição da amplitude dos ângulos. Mais uma vez, o grupo das alunas, Maria e Berta, necessitou de ajuda, quer dos colegas Pedro e José, quer da professora, para operacionalizar esse procedimento. No entanto, foi o único grupo que desenvolveu signos de artefacto baseados em esquemas de ação instrumentada, quando usaram os esquemas de uso (medição dos ângulos), pois utilizaram significados pessoais fundamentados no facto dos ângulos A (do triângulo [ABC]) e DBA e os ângulos C (do triângulo [ABC]) e CBE serem congruentes ( 𝐴 = D 𝐵 A e 𝐶 = C 𝐵 E), por se tratarem de ângulos alternos internos (Figura 3 e Figura 4).
Tendo em consideração, o facto de estarem a trabalhar num Ambiente de Geometria Dinâmica (AGD), todos os alunos usaram o esquema de ação instrumentada evidenciado pela ferramenta de arrastamento, movendo os vértices do triângulo [ABC] para concluir a generalização da congruência dos ângulos, em qualquer outro triângulo (ver Figura 3, Figura 4, Figura 5, Figura 6 e Figura 7). Mas, somente no par, Maria e Berta, é que o esquema de ação instrumentada evidenciado pela ferramenta de arrastamento permitiu a movimentação de significados pessoais para significados matemáticos. Estas alunas, num primeiro contacto com a tarefa, possivelmente, através do esquema de ação instrumentada, ferramenta de visualização, desenvolveram significados pessoais ao percecionarem que os ângulos eram alternos internos e portanto, sempre congruentes. Esses significados pessoais transitaram para significados matemáticos, ao generalizar-se a propriedade: “Em qualquer triângulo, ângulos alternos internos são sempre congruentes”, na discussão coletiva (ver Figura 10 e diálogo 21 - 29).
O par do José e do Pedro, chegam a essa conclusão, possivelmente, porque inicialmente foram medir todos os ângulos, pois não se lembraram do conceito de ângulos alternos internos, que foi abordado no 5.º ano de escolaridade.
No que concerne à alínea d), todos os alunos desenvolveram esquemas de ação instrumentada, ao fazerem emergir os significados pessoais fundamentados no facto dos ângulos DBA, ABC e CBE serem suplementares e a soma das suas amplitudes ser um ângulo raso. Para operacionalizarem esses esquemas de ação instrumentada, desenvolveram esquemas de uso, como se pode percecionar no diálogo entre as duas alunas:
10.Maria: Somei os ângulos na minha calculadora [científica] e deu 180º.
11.Berta: Calma! Podes fazer tudo nesta [calculadora gráfica]! Para escreveres os ângulos DBA +ABC+CBE, podes fazer menu, ações e texto. Depois para calculares a soma total, podes fazer menu, ações e calcular!
12.Maria: Estás a ver, dá sempre 180º, mesmo quando movimentamos os vértices do triângulo e apanhamos outro triângulo.
Ambos os grupos, recorrendo ao uso de papel e lápis, conseguiram mobilizar os significados matemáticos confirmados nas alíneas b) e c). Partindo das relações: 𝐴 = D 𝐵 A, 𝐵 = A 𝐵 C e 𝐶 = C 𝐵 E, concluíram que 𝐴 + 𝐵 + 𝐶 = 180º, através de escrita simbólica, evidenciada por representações simbólicas (Figura 8). No entanto, não utilizaram a calculadora gráfica para confirmar, a igualdade anterior, isto é, que em qualquer triângulo, a soma da medida das amplitudes dos ângulos internos de um triângulo é igual a um ângulo raso.
2ª aula - Produção coletiva de signos - Discussão Matemática
Depois da professora ter lido as produções escritas de cada aluno, deu-se a discussão coletiva. Nesta fase operacionalizou-se um processo de mediação semiótica que consistiu em promover a emergência de signos pessoais relacionados com o uso do artefacto, evoluindo para signos matemáticos, num ambiente social de aprendizagem, a aula. Gerou-se uma polifonia de vozes.
Na ação de retorno à tarefa (diálogo 13-16), a professora solicitou a intervenção dos alunos para fazerem os seus relatos, relativamente à tarefa realizada. A Maria ofereceu-se para assumir a função de aluna Sherpa (Drijvers & Trouche, 2008) que consistiu em resolver a tarefa no computador da professora, com a calculadora gráfica projetada no quadro interativo, onde todos os alunos tiveram a oportunidade de visualizar e acompanhar os raciocínios desenvolvidos (ver Figura 9, Figura 10, Figura 11 e Figura 12). A professora aceitou o pedido da Maria porque na realização da tarefa, a aluna tinha mostrado algumas dificuldades na apropriação do artefacto, calculadora gráfica (Drijvers & Trouche, 2008).
13.Professora: Então, quem quer explicar o que se pretendeu com esta tarefa?
14.Pedro: Mostrar que a soma dos ângulos internos de um triângulo é sempre 180º.
15.Professora: E para isso, tiveram que fazer um conjunto de procedimentos na calculadora gráfica e não só, também com o papel e lápis. Maria, explique então aos seus colegas como resolveu a tarefa!
16.Maria: Para construir o triângulo, eu fui a menu, formas e triângulo. Para traçar a reta paralela, fiz menu, construção e paralela. Depois para marcar os pontos A, B, C, D, E, fiz menu, ações e texto.
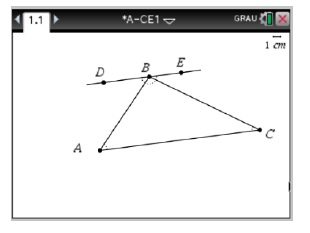
Figura 10: Resolução da Maria, na calculadora gráfica, na alínea a), da tarefa, enquanto aluna Sherpa.
A Maria mostrou uma evolução significativa no que concerne às dificuldades inicialmente sentidas, relativamente ao reconhecimento de certas funções e potencialidades da calculadora gráfica. Temos a perceção que foram ultrapassadas quando assumiu a função de aluno Sherpa e desenvolveu esquemas de uso na construção do triângulo [ABC], na resolução da alínea a) da tarefa. A aluna foi influenciada pelas potencialidades do artefacto, calculadora gráfica, e reconheceu-as para resolver a tarefa, no que respeita à parte instrumental da mesma.
Mais uma vez deu-se uma ação de retorno à tarefa:
17.Professora: Muito bem, Maria! Acabaste de resolver a alínea a). Quem me consegue dizer o que foi pedido nas alíneas b) e c)?
18.José: Foi mostrar que o ângulo A é igual ao ângulo DBA e o ângulo C é igual ao ângulo CBE.
19.Professora: E porque é que têm a mesma amplitude?
20.José: Porque fomos à máquina e fizemos menu, medição, ângulo e medimos e verificamos a igualdade. Depois arrastarmos os vértices do triângulo e deu sempre igual. Eu até fiz no relatório dois exemplos diferentes (ver Figura 6 e Figura 7).
21.Berta: Stora, os ângulos são sempre iguais porque são alternos internos.
Nesta etapa operacionalizou-se uma ação de focalização:
22.Professora: Berta, explica melhor! Porque é que os ângulos são alternos internos? Quais os ângulos que são alternos internos?
23.Berta: Aí stora, não sei explicar. É … por causa da posição deles.
24.Maria: Stora, a reta DE é paralela à reta AC e essas retas são intersetadas por uma reta obliqua AB. Portanto, o ângulo A do triângulo [ABC] tem a mesma medida que o ângulo DBA e o ângulo C do triângulo [ABC] tem a mesma medida que o ângulo CBE.
25.Professora: Maria, mostra aos teus colegas na calculadora gráfica, a veracidade dessa tua conjetura!
A Maria seguiu a sugestão da professora. A aluna utilizou o esquema de ação instrumenta evidenciado pela ferramenta de arrastamento, movimentou os vértices A, B e C, tendo obtido triângulos com diferentes dimensões. Mostrou que a medida da amplitude do ângulo A do triângulo [ABC] é a mesma que a medida da amplitude do ângulo DBA, assim como a medida da amplitude do ângulo C do triângulo [ABC] é a mesma que a medida da amplitude do ângulo CBE (Figura 11).
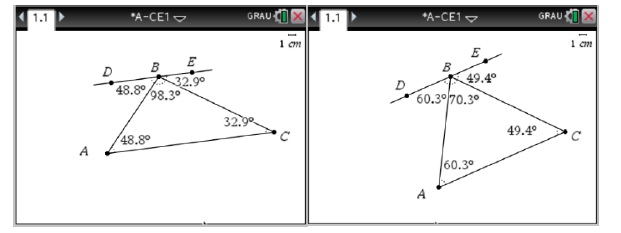
Figura 11: Resolução da Maria, com a calculadora gráfica das alíneas b) e c) na tarefa (utilização da ferramenta de arrastamento).
De seguida a professora solicitou uma síntese e ao mesmo tempo ofereceu uma síntese:
26.Professora: Bom então, voltando à nossa tarefa, podemos dizer que se verifica sempre a congruência desses ângulos?
27.Maria: Quando movimentamos os vértices do triângulo [ABC] os valores alteram-se, mas continua a ser sempre o ângulo A congruente com o ângulo DBA e o ângulo C congruente com o ângulo CBE.
28.Professora: Queres dizer que utilizaste a função de
arrastamento da calculadora gráfica essa propriedade
verifica-se para qualquer triângulo, certo?
29.Maria: Certo!
De novo a professora solicitou a ação de retorno à tarefa:
30.Professora: Então como concluíram a tarefa, com a resolução da alínea d)?
31.Pedro: Os ângulos DBA, ABC e CBE são suplementares e a soma deles é um ângulo raso! É um ângulo de 180º.
A professora solicitou uma síntese:
32.Professora: Essa propriedade acontece sempre em qualquer triângulo?
33.Pedro: Sim, dá sempre 180º, mesmo quando movimentamos os vértices do triângulo [ABC], quer dizer, quando usamos a função de arrastamento.
34.Professora: Mas, como é que essa propriedade vai interferir relativamente à soma das medidas dos ângulos internos do triângulo [ABC] que é o objetivo da alínea d)?
35.Pedro: Stora veja lá como eu justifiquei no meu relatório (figura 9)!
36.Professora: Certo! Mas fizeste uma prova com papel e lápis! E confirmaste a tua conjetura na calculadora gráfica?
37.Pedro: Não! Isso não fiz!
A professora ofereceu uma síntese e a seguir evidenciou uma ação de retorno à tarefa:
38.Professora: Muito bem Pedro! Verificaste que a soma das medidas das amplitudes dos ângulos DBA, ABC e CBE é sempre 180º, em qualquer triângulo, ao usares a função de arrastamento nos vértices A ou B ou C do triângulo[ABC]. Por outro lado, tendo em conta que provaste na alínea b) que 𝐴 = D 𝐵 A e na alínea c) que 𝐶 = C 𝐵 E e sabendo que 𝐵 = A 𝐵 C, concluíste que 𝐴 + 𝐵 + 𝐶 = 180º. Mas, seria interessante utilizarem a calculadora gráfica para confirmar se 𝐴 + 𝐵 + 𝐶 = 180º, em qualquer triângulo.
39.Professora: Alguém fez?
De acordo com a oferta de uma síntese da professora, a Maria continuou a resolver a tarefa, verificando a veracidade da afirmação da docente. A aluna desenvolveu esquemas de uso, ao determinar o valor da soma D 𝐵 A + A 𝐵 C + C 𝐵 E e o valor da soma de 𝐴 + 𝐵 + 𝐶 , dando ambos 180º. Posteriormente, desenvolveu o esquema de ação instrumentada evidenciado pela ferramenta de arrastamento, para confirmar que essas somas se verificam em qualquer triângulo ( Figura 12).
Enquanto a Maria resolveu a tarefa no computador, projetando a solução no quadro interativo, os outros alunos da turma também confirmaram na calculadora gráfica a veracidade da prova, que tinham evidenciado com papel e lápis.

Figura 12: Resolução da Maria, com a calculadora gráfica (utilização da função de arrastamento), na alínea d) da tarefa.
Para finalizar, a professora ofereceu uma síntese, que resultou das diversas soluções dos alunos, discutidas coletivamente, no ambiente social, a aula.
40.Professora: Portanto, a soma das medidas das amplitudes dos ângulos DBA, ABC e CBE é sempre 180º, em qualquer triângulo, ao ser usada a função de arrastamento nos vértices A ou B ou C do triângulo [ABC]. Por outro lado,
CONCLUSÕES
A análise dos dados mostrou que o artefacto, calculadora gráfica funcionou como um instrumento de mediação semiótica. Os alunos ao manipularem este artefacto, desenvolveram o raciocínio matemático, a comunicação matemática e representações simbólicas , ativas e icónicas . Deste modo mobilizaram esquemas de uso e esquemas de ação instrumentada evidenciados através da ferramenta de visualização e ferramenta de arrastamento. Por conseguinte, os esquemas traduziram-se no emergir de significados pessoais (signos de artefacto), nomeadamente nos conceitos de triângulo, retas paralelas, ângulos alternos internos, ângulos suplementares e ângulos rasos.
A participação dos alunos na discussão coletiva favoreceu o desenvolvimento do seu discurso matemático, proporcionando uma evolução na construção dos termos matemáticos esperados. Também nesta fase, a orquestração da professora, ajudada pelo aluno Sherpa, foi determinante pela transição dos signos de artefacto para signos matemáticos, dando-se a construção do conhecimento matemático, verificando-se desta forma, o desenvolvimento do potencial semiótico do artefacto.
O potencial semiótico da calculadora gráfica, proporcionado pela ferramenta de visualização dos ecrãs da calculadora e da ferramenta de arrastamento, potenciado pelo AGD, facilitou a construção do conhecimento, isto é, verificou o objetivo da tarefa em outros triângulos, ao contrário do que aconteceria com os artefactos papel e lápis. Ao arrastar um ponto básico, toda a figura foi transformada, no entanto, todas as propriedades definidas pelo procedimento de construção foram mantidas, ou seja, invariantes. A ferramenta de arrastamento proporcionou a verificação desta propriedade em todos os triângulos, podendo a mesma ser relacionada com o significado teórico da sua construção geométrica dentro da Geometria Euclidiana Mariotti, 2012). Neste sentido, a observação de que a soma das medidas das amplitudes dos ângulos internos de um triângulo é igual a um ângulo raso, em qualquer triângulo, teve como contrapartida a validação a generalização de que: “Em qualquer triângulo, a soma das medidas das amplitudes dos ângulos internos de um triângulo é igual à amplitude de um ângulo raso”, na teoria da Geometria Euclidiana.