Serviços Personalizados
Journal
Artigo
Indicadores
Links relacionados
Compartilhar
Revista Portuguesa de Ciências do Desporto
versão impressa ISSN 1645-0523
Rev. Port. Cien. Desp. v.10 n.1 Porto 2010
Modelo 3D para quantificação das forças articulares e momentos proximais resultantes para o membro superior
Daniel Cury Ribeiro e Jefferson Fagundes Loss
Universidade Federal do Rio Grande do Sul, Escola Superior de Educação Física, Porto Alegre – RS, Brasil
RESUMO
Objetivos: Este estudo teve como objetivo implementar um modelo biomecânico, de segmentos articulados, associado à dinâmica inversa que permita a análise em três dimensões das forças de reação proximais e momentos proximais resultantes para diferentes gestos do membro superior. Método: Os gestos avaliados foram: flexão, extensão e abdução de ombro e flexão de cotovelo, os quais foram realizados por um indivíduo do sexo masculino. O modelo implementado é composto por cinco segmentos rígidos (mão, antebraço, braço, escápula e tronco) conectados. As equações de movimento de Newton-Euler foram utilizadas para quantificação das forças e momentos proximais resultantes. Para registro cinemático foram utilizadas cinco câmeras digitais, com freqüência de amostragem de 50 campos/seg. A precisão estimada do sistema de videogrametria foi, em média, de 1,7 mm. Foi monitorada a atividade eletromiográfica dos músculos deltóide (anterior, médio e posterior), bíceps braquial, tríceps braquial e peitoral maior. O modelo foi avaliado através da comparação qualitativa dos resultados de momento proximal resultante, com a atividade eletromiográfica. Resultados: Os resultados sugerem que o modelo apresenta resultados coerentes. O sinal eletromiográfico e o momento proximal apresentam sincronismo temporal. Conclusão: O modelo foi capaz de estimar as forças de reacção e momentos proximais resultantes nos diferentes gestos.
Palavras-chave: membro superior, eletromiografia, dinâmica inversa 3D
3D model for analysis of resultant proximal reaction forces and moments for the upper limb
ABSTRACT
Objectives: The aim of this study was to implement a biomechanical model, with linked segments associated with inverse dynamics, to analyze proximal net forces and moments during different upper limbs activities. Methods: one male subject performed flexion, extension and abduction of the shoulder and flexion of the elbow. The model is composed of five connected rigid segments (hand, forearm, arm, scapula and trunk). The Newton-Euler motion equations were used to quantify proximal net reaction forces and moments. For kinematics recording, five cameras with a frequency sample of 50 fps were used. Videogrammetry accuracy was, on average, 1,7mm. The following muscles had their activities monitored: deltoid (anterior, medial, posterior), biceps brachialis, triceps brachialis, pectoralis major. The model was evaluated by qualitative comparison of proximal net moments with electromyographic signal of agonist muscles. Results: The results showed a temporal synchronism between the proximal net moments and agonist EMG activity. Conclusions: The model was able to estimate proximal net forces and moments during different upper limbs activities.
Key-words: upper extremity, electromyography, inverse dynamics 3D
INTRODUÇÃO
O modelamento de membros superiores tem sido feito utilizando diferentes tipos de modelos: segmentos articulados, neuromusculares e músculo-esquelético(7, 16, 25, 30). O tipo de modelo depende, claramente, do objetivo da pesquisa. Nos casos em que o interesse é quantificar a parcela de contribuição de cada músculo no momento muscular resultante, o modelo utilizado é o neuromuscular ou músculo-esqueléticos(4, 7, 13, 15).
A avaliação das forças de reação proximais (Frp) resultantes e momentos proximais (Mp) resultantes tem sido feita comumente através de modelos de segmentos articulados(22, 26). Este tipo de modelo parece ser útil para avaliação das cargas articulares(29), ou então, para avaliação de estratégias motoras em atividades esportivas(9). Para avaliação de estratégia motora em gestos esportivos, a informação mais relevante que o modelo oferece são os Mp (9), enquanto para avaliação das cargas impostas às articulações, a informação mais relevante que o modelo oferece são as Frp(11). A preocupação em quantificar as forças articulares volta-se, justamente, para a melhor compreensão dos mecanismos de lesão articulares(6, 22) e elaboração de próteses articulares.
Todo modelo carece de uma validação, pois a mesma confere maior confiabilidade aos resultados fornecidos. Segundo Nigg e Herzog(23) a validação pode ser feita de três formas: medições diretas, indiretas ou de tendência. A comparação dos resultados contra medições diretas é um processo por vezes inviável, por restrições éticas e tecnológicas. Isto se torna ainda mais crítico quando se trata de modelos que visam estimar as forças internas do corpo, como de reação proximal ou articulares dos segmentos corporais. As medições indiretas prevêem a medição de outra variável associada que possa ser obtida e comparada com o valor predito pelo modelo, como uma força externa por exemplo. A crítica a este procedimento é que não há garantias que o valor predito para a variável de interesse seja confiável. As medidas de tendências podem ser uma alternativa quando o valor absoluto predito pelo modelo não é o fator mais importante, mas o comportamento das variáveis durante a situação analisada(18).
Alguns autores utilizam o sinal eletromiográfico para avaliar o modelo utilizado através da comparação entre o Mp e a atividade eletromiográfica dos músculos agonistas do movimento(29, 31, 32). Para modelos mais simples, como é o caso de modelos de segmentos rígidos, parece existir uma concordância temporal entre o sinal eletromiográfico e o Mp(29).
Recentemente, Veeger e Pascoal(34) relataram que o número de publicações referentes aos membros superiores é menor que o número de publicações voltadas para os membros inferiores. Isso sugere que existe a necessidade de dedicar parte das pesquisas, na área da biomecânica, para análises do membro superior. Portanto, este trabalho tem como objetivo implementar um modelo de segmentos articulados para o membro superior. A validação do modelo será feita através da comparação qualitativa entre atividade eletromiográfica e Mp.
MATERIAIS E MÉTODOS
A amostra foi constituída por um sujeito do sexo masculino de idade de 25 anos, 1,79 metros de altura e 80 kg, o qual realizou quatro diferentes gestos motores. Optou-se por gestos comumente utilizados na prática da musculação e reabilitação. Os gestos avaliados foram: flexão, extensão e abdução de ombro e flexão de cotovelo. Cada gesto foi realizado cinco vezes. Antes de qualquer envolvimento com este trabalho, o indivíduo assinou o Termo de Consentimento Informado, consentindo formalmente na participação desta pesquisa. Foram coletados, junto à videogrametria, o sinal eletromiográfico dos seguintes músculos: deltóide anterior (DA), deltóide médio (DM), deltóide posterior (DP), bíceps braquial (BB), tríceps braquial (TB) e peitoral maior (PM).
Para aquisição dos dados cinemáticos foram utilizadas cinco câmeras de vídeo (JVC GR-DVL9800). O tempo de abertura das câmeras (shutter) foi ajustado em 1/250, com freqüência de amostragem de 50 campos/seg. No suporte de cada câmera, foi fixado um iluminador com mesma direção óptica da câmera para aumentar o contraste entre o marcador reflexivo e o restante da imagem. A digitalização das imagens e reconstrução espacial foram feitas no software Dvideow (10). O modo de digitalização das imagens foi semi-automático, sendo adotados os seguintes algoritmos: inversão, erosão, getmarkers (2). A reconstrução espacial foi feita através do método DLT (1) utilizando um padrão de calibração 3D da Peak Performance, com sensibilidade de um décimo de milímetro. A precisão do sistema de videogrametria foi de 1,5 mm, calculada através do desvio padrão de 1000 medições (20 segundos de filmagem consecutiva) realizadas sobre um bastão rígido de 246,5 mm de comprimento, movimentado dentro do volume de calibração, conforme procedimento sugerido por Andrade e colaboradores(2). Os dados cinemáticos foram filtrados com filtro digital passa-baixa Butterworth, ordem 3. A freqüência de corte foi determinada através do método da Análise Residual, proposto por Winter(35). Através deste método, foi determinado um valor de freqüência de corte para cada coordenada espacial global (X, Y, Z) de cada referência anatômica, em cada gesto realizado. As freqüências de corte variaram de 0,5 à 4,9 Hz. A determinação das referências anatômicas foi feita através de marcadores retroreflexivos em formato de esfera com 15 mm de diâmetro. As referências anatômicas utilizadas foram: sétima vértebra cervical (C7); oitava vértebra torácica (T8); processo coracóide (PC); incisura jugular (IJ); processo xifóide (PX); articulação esternoclavicular (SC); articulação acrômio-clavicular (AC); ângulo medial da escápula (AM); ângulo inferior da escápula (AI); epicôndilo lateral (EL); epicôndilo medial (EM); processo estilóide do rádio (PER); processo estilóide da ulna (PEU); gleno-umeral (GU) estimado através do método de regressão linear(21). Para evitar imprecisões da localização dos pontos do epicôndilo lateral (EL) e epicôndilo medial (EM), em virtude da movimentação da massa muscular subjacente aos marcadores retroreflexivos, foi utilizado um marcador técnico (MT) no segmento do braço(27).
Foram utilizados três tipos de sistemas de coordenadas. O sistema de coordenadas global (SCG) é o sistema de referência do laboratório. Cada segmento (mão, antebraço, braço, escápula e tronco) apresenta um sistema de coordenadas local (SCL) engastado e alinhado aos eixos principais de inércia do mesmo. Desta forma, o eixo X é o eixo póstero-anterior; Y é o eixo vertical (para o SCG) ou longitudinal ao segmento (para o SCL); Z é o eixo médio-lateral. O sistema de coordenadas local (SCL) para cada segmento foi definido, conforme recomendação da Sociedade Internacional de Biomecânica (36). Por último, o sistema de coordenadas articular (SCA), proposto por Grood e Suntay(12), é um sistema não ortogonal e foi utilizado para proporcionar um significado cinesiológico aos dados de Mp.
Para determinar os ângulos articulares e descrever a orientação dos segmentos no espaço, foram utilizadas as seqüências de rotações sugeridas por Wu e colaboradores(36). A posição anatômica foi adotada como posição referência (zero graus). O movimento de prono-supinação é descrito como o movimento do rádio em relação à ulna. No presente modelo, o antebraço foi considerado como um único segmento. Portanto, o movimento de prono-supinação é considerado como a rotação do antebraço em torno do seu eixo longitudinal(5).
O modelo implementado foi denominado de MOSA-MS (Modelo de Segmentos Articulados – Membro Superior) e conta com cinco segmentos rígidos (mão, antebraço, braço, escápula e tronco) conectados. Dentro do modelo, o membro superior foi considerado como possuindo sete graus de liberdade. Os três graus de liberdade do ombro são atribuídos à abdução-adução, flexão-extensão e rotação interna e externa do úmero em relação ao tronco. Dois graus de liberdade do cotovelo correspondem à flexão-extensão e prono-supinação, enquanto que o punho apresenta dois graus de liberdade referentes aos desvios ulnar-radial e flexão-extensão(5). A partir da massa do indivíduo, foram estimadas as massas, momento de inércia e localização do centro de massa para cada segmento (mão, antebraço, braço, escápula e tronco) com base em dados antropométricos da literatura(37). As equações de movimento utilizadas no modelo foram as de Newton-Euler(35, 37). Estas equações regem o modelo e permitem a quantificação das Frp e Mp. As equações (1) e (2) regem o movimento linear e o movimento angular:

Em que: SF é o somatório das forças aplicadas; m é a massa;
acm é a aceleração linear do centro de massa;
SM é o somatório dos momentos aplicados;
![]() é a taxa de variação do momento de inércia.
é a taxa de variação do momento de inércia.
Com excepção da massa, todas as grandezas são vectoriais.
Dentro do MOSA-MS, os dados cinemáticos, cinéticos e antropométricos são utilizados como variáveis independentes do modelo. As variáveis dependentes são as Frp e Mp envolvidos. Considerando que em cada segmento rígido, além das forças inerciais e da força peso do próprio segmento, existem dois momentos resultantes (um proximal e outro distal) e duas forças resultantes (uma proximal e outra distal), pode-se re-escrever a equação (1) em relação a cada eixo de coordenada, conforme as equações (3), (4) e (5). No entanto, a força peso atua apenas no eixo y.
Frpx + Frdx = max (3)
Frpy + Frdy + P = may (4)
Frpz + Frdz = maz (5)
Em que: x,y ou z (subscrito) é o eixo de coordenada;
Frp é a Força de reação proximal; Frd é a Força de reação distal;
P é a Força peso do segmento; m é a massa do segmento;
a é a aceleração do CM do segmento.
Conhecidas as acelerações lineares, a força peso do segmento e a força distal que atua sobre o mesmo, a variável Frp se torna a única incógnita. As equações (3, 4 e 5) são aplicadas para análise das forças que envolvem um único segmento. Conforme o número de segmentos aumenta, dentro da cadeia cinética, a complexidade das equações de movimento se torna proibitiva. Desta forma, o procedimento adotado é a repetição da aplicação destas equações para cada segmento, um por vez(37). O cálculo destas equações, dentro da dinâmica inversa, respeita a ordem distal – proximal. Assim, a força externa (Fe) no segmento distal é representada na equação por Frd (Equações 3, 4, e 5).
Com a finalidade de evitar confusões de nomenclatura, o segmento proximal será denominado de segmento i e o segmento distal de segmento i+1 (Figura 1). Assim, dado um segmento i+1, a força externa é considerada como força distal (Frd) e a Frp é a única incógnita na equação (Equações 3,4 e 5). A força distal do segmento adjacente i é a força de reação proximal do segmento i+1. A Frd do segmento i apresenta a mesma magnitude que a Frp do segmento i+1, porém, com sentido contrário. Desta maneira, é possível o cálculo das forças de reação proximal resultantes das articulações proximais(35, 37).
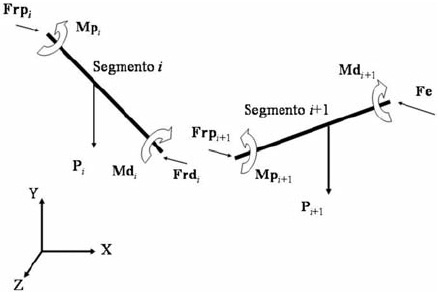
Figura 1. Diagrama cinético representando a lei de ação e reação para as forças e momentos. Pi: peso segmento i; Pi+1: peso segmento i+1; Mdi: momento distal segmento i; Mdi+1: momento distal segmento i+1; Mpi: momento proximal segmento i; Mpi+1: momento proximal segmento i+1; Frdi: força de reação distal segmento i; Frdi+1: força de reação distal Segmento i+1; Frpi: força de reação proximal segmento i; Frpi+1: força de reação proximal segmento i+1; Fe: força externa.
As equações de movimento lineares foram calculadas em relação ao SCG, no entanto são analisados em relação a um sistema de coordenadas fixado ao segmento (sistema de coordenadas local)(37). Para isso, utiliza-se a mudança de base de um sistema de coordenadas global para outro local, conforme a equação (6):
![]()
Em que: [Fr]L é a força de reação resultante (x, y, z) no sistema de coordenadas local;
[R]T é a transposta da matriz de rotação determinada pela relação de orientação espacial entre o sistema de coordenadas local do segmento e o sistema de coordenadas global;
[Fr]G é a força de reação resultante (X, Y, Z) no sistema de coordenadas global.
Um procedimento semelhante é realizado para o cálculo de Mp. A equação (2) refere-se aos momentos envolvidos em cada segmento. Esta equação refere-se ao efeito rotacional que as forças e momentos aplicados ao segmento impõem ao mesmo. A solução das equações de movimento angular respeita também a ordem distal-proximal. A resolução da equação de movimento angular é descrita em relação ao SCL (25). As equações (7), (8) e (9) foram utilizadas para o cálculo do momento:
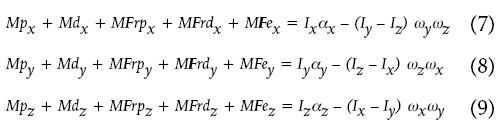
Em que: x, y ou z (subscrito) é o eixo de coordenada local;
Mp é o momento proximal em relação ao eixo subscrito do SCL;
Md é o momento distal em relação ao eixo subscrito do SCL;
MFrp é o momento causado pela força de reação proximal em relação ao eixo subscrito do SCL;
MFrd é o momento causado pela força de reação distal em relação ao eixo subscrito do SCL;
MFe é o momento causado pela força externa em relação ao eixo subscrito do SCL;
I é o momento de inércia do segmento em relação ao eixo subscrito do SCL;
a é a aceleração angular do segmento em relação ao eixo subscrito do SCL;
w é a velocidade angular do segmento em relação ao eixo subscrito do SCL.
Visto que o centro de rotação, para fins de cálculo, é o centro de massa do segmento, a força peso do mesmo não gera momento algum. A discriminação das forças que geram momentos torna o Mp a única incógnita na equação (2). Este momento líquido pode ser interpretado como o momento produzido pelos músculos, ligamentos e cápsula nesta articulação, desde que os movimentos sejam realizados em baixas velocidades e as amplitudes não sejam extremas. Na medida em que as equações de momento são feitas em relação ao SCL de cada segmento, é necessário expressar o momento proximal do segmento i+1 para o SCG, para depois, re-expressá-lo, rodado, no SCL do segmento i(37). Para isso, utiliza-se a equação (10):
![]()
Em que: [Mp]G é o momento proximal no sistema de coordenadas global;
[R] é a matriz de rotação determinada pela relação de orientação espacial entre o sistema de coordenadas local do segmento e o sistema de coordenadas global;
[Mp]L é o momento proximal no sistema de coordenadas local.
O MpG do segmento i+1 é o MdG do segmento i com sentido contrário (Figura 1). Para tornar possível o cálculo do MpG do segmento i, o MdG deve estar expresso no SCL deste segmento. Para isso, a equação (11) é utilizada:
![]()
Em que: [Md]L é o momento distal (x, y, z) no sistema de coordenadas local;
é a transposta da matriz de rotação, determinada pela relação de orientação espacial entre o sistema de coordenadas local do segmento e o sistema de coordenadas global;
[Md]G é o momento distal (X, Y, Z) no sistema de coordenadas global.
Os resultados de Mp apresentados estão expressos em relação ao SCA (equações 12, 13 e 14) visto que o Mp expresso no SCL não apresenta vínculo direto com a nomenclatura anatômica(12, 33).
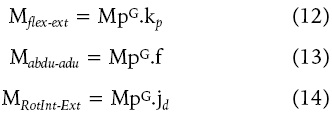
Em que: Mflex-ext é o momento flexor / extensor;
Mabdu-adut é o momento abdutor / adutor;
MRotInt-Ext é o momento rotação interna / externa;
MpG é o momento proximal expresso no SCG;
kp é o vetor unitário k do segmento proximal;
f é o eixo flutuante;
jd é o vetor unitário j do segmento distal.
O eletromiógrafo (Bortec Eletronics Inc., Calgary, Canadá) foi conectado a um conversor A/D, Dataq, modelo DI-720-USB (Dataq Instruments Inc., EUA). A freqüência de amostragem do sinal eletromiográfico foi de 2000 Hz por canal. Para o registro dos sinais eletromiográficos foram observados os padrões sugeridos recomendados pela Sociedade Internacional de Eletrofisiologia e Cinesiologia(20) e aqueles sugeridos pela Sociedade Internacional de Biomecânica(28). Em relação ao posicionamento dos eletrodos, na área determinada para a fixação dos mesmos, foi feita tricotomia e higienizada com algodão embebido em álcool, para redução da impedância da pele e melhor captação do sinal eletromiográfico. Os eletrodos, em configuração bipolar, foram posicionados paralelos às fibras musculares nos ventres dos músculos DA, DM, DP, BB, TB e PM.
O sincronismo entre as câmeras foi feito através do canal de áudio(3). O sincronismo entre a cinemetria e eletromiografia foi feito através de um sincronismo eletrônico, conectado no mesmo conversor A/D do eletromiógrafo(18). Os dados de eletromiografia foram processados no software SAD32. Os dados de eletromiografia foram filtrados com filtro digital passa banda, Butterworth, com freqüência de corte entre 20 e 600Hz, ordem 3. O sinal eletromiográfico foi quantificado através do valor RMS, em intervalos de 500 milisegundos, com janelamento Hamming. O sinal eletromiográfico, já suavizado, foi normalizado pela contração voluntária máxima (CVM) de cada porção muscular (DA, DM, DP, BB, TB, PM).
Para processamento dos dados de eletromiografia e cinemetria foram utilizados os softwares SAD32, Matlab ®7.0 e Dvideow. Para elaboração e aplicação do modelo proposto foi utilizado o software Matlab® 7.0. Para contornar as diferenças de freqüência de amostragem utilizadas para cada instrumento de medida (eletromiográfo e videogrametria) foi necessário subamostrar os dados de eletromiografia (já processados) para 50 Hz. Este processamento não comprometeu os dados de EMG, com relação às componentes de freqüências, pois estas já haviam sido eliminadas por ocasião do processamento prévio(19). A validação do modelo foi feita através da comparação quantitativa de resultados parciais que o modelo oferece juntamente aos resultados obtidos com outros instrumentos não invasivos(23). Qualitativamente os resultados oferecidos pelo modelo foram comparados com o sinal de eletromiografia(29).
RESULTADOS E DISCUSSÕES
A seguir serão apresentados os resultados de força de reação resultante e resultados de momento proximal resultante obtidos através do modelo. O MOSA-MS estima a magnitude da força de reação proximal e momento proximal resultante para cada articulação do membro superior (punho, cotovelo, ombro). Os resultados referentes aos movimentos de abdução e extensão de ombro são apresentados na Tabela 1. Os resultados de Frp e Mp referentes aos gestos de flexão de ombro e de cotovelo são apresentados e discutidos em mais detalhes (Figuras 2-6), visto que os mesmos foram utilizados para validação do MOSA-MS. A seguir, o sistema de coordenadas local do antebraço será referenciado como xa, ya, za enquanto o sistema de coordenadas local do braço será referenciado como xb, yb, zb.
Tabela 1. Valores de pico de cada componente de Frp e Mp para o segmento do braço durante os gestos de abdução e extensão de ombro e ângulo de elevação de ombro correspondente.
| Movimento | |||
|
|
| Abdu | Ext |
|
| x | 13,83 | -4,52 |
|
|
| (-79,28°) | (-16,77°) |
| Frp (N) | y | 38,03 | 38,88 |
|
|
| (-13,63°) | (-14,44°) |
|
| z | 38,08 | 8,56 |
|
|
| (-78,98°) | (-16,60°) |
|
| x | -10,33 | -2,47 |
|
|
| (-77,47°) | (-16,71°) |
| Mp (Nm) | y | -0,26 | -0,23 |
|
|
| (-12,12°) | (-43,02°) |
|
| z | 3,89 | -0,41 |
|
|
| (-12,12°) | (-13,65°) |
Frp: força de reação proximal; Mp: momento proximal.
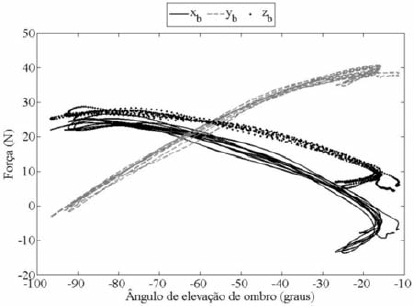
Figura 2. Força de reação proximal (Frp) do braço durante as 5 repetições do gesto de flexão de ombro. Valores de força expressos no sistema de coordenadas local do braço. xb, yb, zb: Sistema cartesiano do segmento do braço.
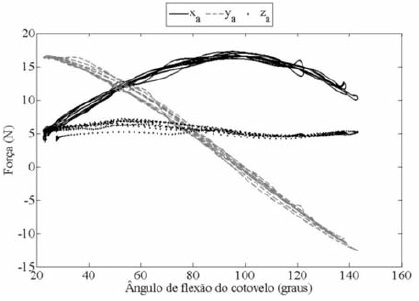
Figura 3. Força de reação proximal (Frp) do braço durante as 5 repetições do gesto de flexão de cotovelo. Valores de força expressos no sistema de coordenadas local do antebraço. xa, ya, za: Sistema cartesiano do segmento do antebraço.
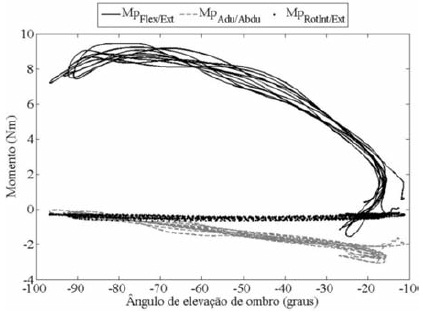
Figura 4. Momento proximal (Mp) do braço durante as 5 repetições do gesto de flexão de ombro. Mp flex/ext: momento proximal flexor (+), extensor (-). Mp abdu/adu: momento proximal adutor (+) e abdutor (‑). Mp rotint/ext: momento proximal rotação interna (+) e rotação externa (-).
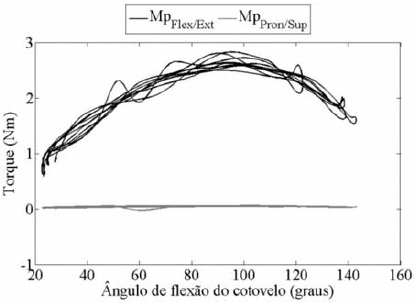
Figura 5. Momento proximal (Mp) do antebraço durante as 5 repetições do gesto de flexão de cotovelo. Mp flex/ext: momento proximal flexor(+), extensor (-). Mp Pront/Sup: momento proximal pronação (+) e supinação (-).
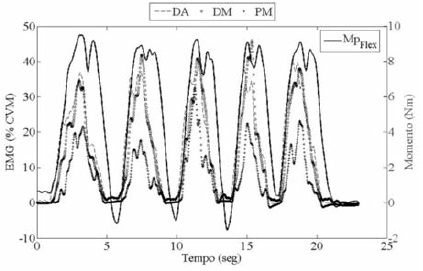
Figura 6. Atividade Eletromiográfica (% da CVM) e momento proximal (expresso no sistema de coordenadas articular) durante o gesto de flexão de ombro. DA: deltóide anterior; DM: deltóide médio; PM: peitoral maior; Mp flex/ext: momento proximal flexor(+), extensor (-).
A Figura 2 apresenta os valores de Frp para a articulação do ombro, durante o gesto de flexão ombro. Quando o ombro se encontra próximo na posição neutra (ângulo de elevação próximo de zero), o maior componente de Frp é o yb (longitudinal, o que representa uma carga de tração na articulação gleno-umeral) e sua magnitude é próxima ao peso do segmento de todo membro superior, aproximadamente 40 N (equivalente a soma do peso dos segmentos mão, antebraço e braço que é de 5% do peso corporal). Quando o indivíduo realiza a flexão de ombro, próximo aos 90° de flexão, o maior componente de Frp é o xb (cisalhamento posterior na articulação gleno-umeral) e zb, com magnitudes muito próximas (sobrecarga compressiva na articulação gleno-umeral). Isso se justifica em virtude da leve rotação externa do ombro (Figura 2).
A Figura 3 apresenta os valores de força de reação resultante para a articulação do cotovelo, durante o gesto de flexo-extensão do cotovelo. A maior componente da Frp quando o cotovelo está próximo à extensão completa é o ya, com valor próximo de 17 N. Esta é a força de reação à força peso dos segmentos da mão e antebraço, que somadas atingem o valor aproximado de 17,5 N. Conforme o indivíduo realiza a flexão de cotovelo, a orientação do eixo xa (perpendicular ao segmento no sentido póstero-anterior) fica mais vertical e a força peso age predominante sobre este eixo. A força no eixo za (perpendicular ao segmento no sentido médio-lateral) é muito baixa, ficando em torno de 5 N, sugerindo mínima sobrecarga de cisalhamento médio-lateral.
É importante destacar que os resultados de Frp são resultantes, eles não se referem às forças de contato internas que agem nos segmentos. A Frp neste modelo contabiliza, apenas, as forças inercial e gravitacional que agem no segmento, na medida em que os esforços musculares acabam neutralizados pelos esforços capsulo-ligamentares. Forças de contato entre superfícies cartilaginosas (por vezes denominadas forças osso-osso), forças ligamento-osso e forças tendão-osso dependem do nível de atividade muscular, a qual não foi analisada isoladamente(8, 31, 37). Não obstante, o gesto analisado no presente estudo é realizado em cadeia cinética aberta (CCA). Desta forma, a Frp, depende única e exclusivamente da aceleração linear e da massa do segmento. Ao contrário, gestos realizados em cadeia cinética fechada (CCF), como por exemplo a marcha (durante a fase de apoio), a Frp depende não apenas da aceleração linear e da inércia do segmento, mas também da força de reação do solo. Esta força, pelo seu sentido de atuação e por ter maior magnitude que o componente inercial, provoca forças compressivas na articulação(35). Para o membro superior, visto que a maior parte dos gestos são realizados em CCA, as Frp são dependentes da força inercial(22). É muito provável que as forças articulares de contato sejam muito maiores que aquelas estimadas em modelos de segmentos articulados associados à dinâmica inversa(37). Além disso, espera-se que o comportamento destas forças seja diferente, em virtude do acréscimo da força muscular na equação de movimento linear(17). Loss e colaboradores(17) compararam os resultados de obtidos através de um modelo de segmentos articulados associado à dinâmica inversa com resultados obtidos com um modelo músculo-esquelético. Ao considerar a atividade muscular, em um gesto em CCA, os autores encontraram forças até 4 vezes maiores que àquelas encontradas pelo modelo de segmentos articulados associado à dinâmica inversa. Fora isso, as forças articulares foram compressivas para o modelo músculo-esquelético, enquanto que o outro modelo encontrou forças de tração no joelho. No entanto, o uso de modelos de segmentos articulados permite uma avaliação quantitativa da sobrecarga articular durante gestos motores.
A Figura 4 apresenta os momentos proximais do ombro durante o gesto de flexão de ombro. O maior momento é o flexor (Mpflexor), atingindo valores próximos a 9,5 Nm. Além disso, o indivíduo parte de uma leve abdução de ombro (Figura 2) e realiza uma adução relativa, expressa pelo momento adutor (Mpadu) relativo (Figura 4). Nos menores ângulos de elevação, existe um momento abdutor pequeno de 3 Nm e este se aproxima de 0 Nm nos maiores ângulos de elevação. Desta maneira, o pico de sobrecarga músculo-tendínea foi entre 70-80° de elevação. Os momentos associados à flexo-extensão de cotovelo estão apresentados na Figura 5. O maior MpFlex ocorre quando o cotovelo encontra-se próximo aos 90° de flexão, como esperado. A magnitude deste momento atinge, aproximadamente, 2,5 Nm.
Na literatura, não encontramos estudos que tenham analisado gestos similares aos apresentados por nosso estudo. No entanto, o modelo de segmentos articulados e dinâmica inversa tem sido aplicado para estimar cargas em diferentes atividades. Por exemplo, Feltner e Taylor(9), da mesma forma que Hong, Cheung e colaboradores(14) e Fleisig e colaboradores(11) utilizaram o modelo de segmentos articulados e dinâmica inversa para avaliar a técnica e sobrecarga articular e músculo-tendínea do arremesso durante gestos de arremesso a partir de um modelo de segmento articulados. Murray e Johnson(22) analisaram a sobrecarga articular e músculo-tendínea em gestos de atividade de vida diária. Estes estudos mostram diferentes aplicabilidades deste tipo de modelo.
Os resultados encontrados entre o sinal eletromiográfico e o Mp sugerem uma boa coerência dos resultados cinéticos do modelo. Outros autores também utilizaram a eletromiografia para avaliar o modelo proposto(29, 31, 32). Para modelos músculo-esqueléticos complexos, a amplitude da eletromiografia não parece ser um método fiável para validação do modelo, devido à relação incerta entre o sinal eletromiográfico e força muscular(31). Para modelos mais simples, como modelo de segmentos articulados, parece existir uma concordância entre o sinal eletromiográfico e o Mp(29). De forma geral, para todos os gestos houve uma sincronia temporal entre o Mp e o sinal eletromiográfico. A Figura 6 apresenta a atividade eletromiográfica dos músculos DA, DM, DP, BB, TB e PM, bem como, do Mp para o gesto de flexão de ombro.
Os resultados mostraram uma atividade sincronizada entre os músculos DA, DM e PM e o Mpflexor (Figura 6). Músculos com maiores distâncias perpendiculares (braço de alavanca efetivo) são considerados motores primários(24).
Os dados do presente trabalho sugerem que o modelo é capaz de avaliar as forças de reação proximal resultantes e momentos proximais resultantes nos diferentes gestos. Quando analisados parcialmente, os resultados oferecidos pelo modelo parecem ser coerentes. A atividade eletromiográfica e o momento proximal líquido apresentaram sincronia temporal, o que sugere uma coerência nos dados de momento proximal do modelo.
AGRADECIMENTOS
Os autores agradecem aos integrantes do Grupo de Biomecânica da ESEF-UFRGS pelo auxílio durante a coleta de dados. Um agradecimento especial à: Fábia Millman, Lizandra C. Bittencourt, Juliana Motta Costa, Joelly Mahnic de Toledo e Marcelo Peduzzi de Castro pela contribuição durante a coleta e digitalização das imagens. Este estudo recebeu apoio financeiro da CAPES.
REFERÊNCIAS BIBLIOGRÁFICAS
1. Abdel-Aziz, and Karara. (1971). Direct linear transformation from comparator coordinates into objects space coordinates in close-range photogrammetry. Proceedings of the Symposium on Close-Range Photogrammetry, 1-18.
2. Andrade LM, Araújo AGN, Barros RML (2004). Análise de marcha: protocolo experimental para posicionamento e orientação dos segmentos do corpo humano baseado em sistemas de marcas técnicas. Brazilian Journal of Biomechanics, 9: 33-40
3. Barros RML, Russomanno TG, Brenzikover R, Figueroa PJ (2006). A method to synchronise video cameras using the audio band. J Biomech, 39: 776-780
4. Bassett RW, Browne AO, Morrey BF, An KN (1990). Glenohumeral muscle force and moment mechanics in a position of shoulder instability. J Biomech, 23(5): 405-415
5. Biryukova EV, Roby-Brami A, Frolov AA, Mokhtari M (2000). Kinematics of human arm reconstructed from spatial tracking system recordings. J Biomech, 33(8): 985-995
6. Buchler P, Ramaniraka NA, Rakotomanana LR, Iannotti JP, Farron A (2002). A finite element model of the shoulder: application to the comparison of normal and osteoarthritic joints. Clin Biomech (Bristol, Avon), 17(9-10): 630-639
7. Chang YW, Hughes RE, Su FC, Itoi E, An KN (2000). Prediction of muscle force involved in shoulder internal rotation. J Shoulder Elbow Surg, 9(3): 188-195
8. Favre P, Sheikh R, Fucentese SF, Jacob HA (2005). An algorithm for estimation of shoulder muscle forces for clinical use. Clin Biomech (Bristol, Avon), 20(8): 822-833
9. Feltner ME, Taylor G (1997). Three-Dimensional kinetic of the shoulder, elbow, and wrist during a penalty throw in water polo. J Applied Biomech, 13: 347-372.
10. Figueroa PJ, Leite NJ, Barros RM (2003). A flexible software for tracking of markers used in human motion analysis. Comput Methods Programs Biomed, 72(2): 155-165
11. Fleisig GS, Andrews JR, Dillman CJ, Escamilla RF (1995). Kinetics of baseball pitching with implications about injury mechanicsms. American Journal of Sports Medicine, 23(2): 233-239
12. Grood ES, Suntay WJ (1983). A joint coordinate system for the clinical description of three-dimensional motions: application to the knee. J Biomech Eng, 105(2): 136-144
13. Hogfors C, Sigholm G, Herberts P (1987). Biomechanical model of the human shoulder--I. Elements. J Biomech, 20(2): 157-166
14. Hong DA, Cheung TK, Roberts EM (2001). A three-dimensional, six-segment chain analysis of forceful overarm throwing. J Electromyogr Kinesiol, 11(2): 95-112
15. Karlsson D, Peterson B (1992). Towards a model for force predictions in the human shoulder. J Biomech, 25(2): 189-199
16. Kaufman KR, An KW, Litchy WJ, Chao EY (1991). Physiological prediction of muscle forces--I. Theoretical formulation. Neuroscience, 40(3): 781-792
17. Loss J, Soares D, Cañeiro JP, Aldabe D, Ribeiro DC, Gandolfi L (2006). O uso da dinâmica inversa em situações envolvendo cadeia cinética aberta. Brazilian Journal of Biomechanics, 7: 23-32
18. Loss JF, Silva LMR, Zaro M, Guimarães ACS (1997). Sincronismo entre eletromiografia e cinemetria. VII Congresso Brasileiro de Biomecânica, 453-456.
19. Loss JF, Zaro M, Godolphim BH, Godolphim B, Michel C (1998). Sugestão de método para correlacionar força muscular e eletromiografia. Movimento, 8: 33-40 [ Links ]
20. Merletti R (1999). Standards for reporting EMG data. Journal of Eletromyography and Kinesiology, 9: 3-4
21. Meskers CG, van der Helm FC, Rozendaal LA, Rozing PM (1998). In vivo estimation of the glenohumeral joint rotation center from scapular bony landmarks by linear regression. J Biomech, 31(1): 93-96
22. Murray IA, Johnson GR (2004). A study of the external forces and moments at the shoulder and elbow while performing every day tasks. Clin Biomech (Bristol, Avon), 19(6): 586-594
23. Nigg BM, Herzog W (1999). Biomechanics of the musculo-skeletal system, 2nd Ed., Wiley, Chichester, U.K.
24. Otis JC, Jiang CC, Wickiewicz TL, Peterson MG, Warren RF, Santner TJ (1994). Changes in the moment arms of the rotator cuff and deltoid muscles with abduction and rotation. J Bone Joint Surg Am, 76(5): 667-676
25. Praagman M, Stokdijk M, Veeger HE, Visser B (2000). Predicting mechanical load of the glenohumeral joint, using net joint moments. Clin Biomech (Bristol, Avon), 15(5): 315-321
26. Rodgers MM, Tummarakota S, Lieh J (1998). Three-Dimensional Dynamic Analysis of Wheelchair Propulsion. J Apllied Biomech, 14: 80-92
27. Schmidt R, Disselhorst-Klug C, Silny J, Rau G (1999). A marker-based measurement procedure for unconstrained wrist and elbow motions. J Biomech, 32(6): 615-621
28. Soderberg, G. L., and Knutson, L. M. (2000). A guide for use and interpretation of kinesiologic electromyographic data. Phys Ther 80 (5):485-498.
29. Sogaard K, Laursen B, Jensen BR, Sjogaard G (2001). Dynamic loads on the upper extremities during two different floor cleaning methods. Clin Biomech (Bristol, Avon), 16(10): 866-879
30. Suzuki M, Yamazaki Y, Matsunami K (2000). Simplified dynamics model of planar two-joint arm movements. J Biomech, 33(8): 925-931
31. van der Helm FC (1994). A finite element musculoskeletal model of the shoulder mechanism. J Biomech, 27(5): 551-569
32. van der Helm FC, Veeger HE (1996). Quasi-static analysis of muscle forces in the shoulder mechanism during wheelchair propulsion. J Biomech, 29(1): 39-52
33. Vaughan CL, Davis BL, O'connor JC (1999). Dynamics of Human Gait, Koboho Publishers.
34. Veeger DJ, Pascoal AG (2006). Upper extremity biomechanics: Are we closing the gap? Proceedings of the 5th meeting of the International Shoulder Group. Clin Biomech (Bristol, Avon), 21: (S1-S2)
35. Winter DA (2005). Biomechanics and motor control of human movement, 3rd Ed., Wiley, Hoboken, NJ
36. Wu G, van der Helm FC, Veeger HE, Makhsous M, Van Roy P, Anglin C, Nagels J, Karduna AR, McQuade K, Wang X, Werner FW, Buchholz B (2005). ISB recommendation on definitions of joint coordinate systems of various joints for the reporting of human joint motion--Part II: shoulder, elbow, wrist and hand. J Biomech, 38(5): 981-992
37. Zatsiorsky VM (2002). Kinetics of human motion, Human Kinetics, Champaign, IL
Daniel Cury Ribeiro
Rua Barão do Amazonas, 793/apt: 401
Bairro Jardim Botânico
Porto Alegre – RS CEP: 90670-004
E-mail: daniel.cury.ribeiro@gmail.com













