ARTÍCULOS

Selección de salvaguardas en gestión del riesgo en sistemas de la información: un enfoque borroso

Safeguard selection for risk management in information systems: a fuzzy approach

 

Antonio Jiménez-Martín ¹, Eloy Vicente, Alfonso Mateos ¹

¹ Grupo de Análisis de Decisiones y Estadística, Departamento de Inteligencia Artificial, Universidad Politécnica de Madrid, Campus de Montegancedo S/N, Boadilla del Monte, 28660, España. E-mail: antonio.jimenez@upm.es, e.vicentecestero@upm.es, alfonso.mateos@upm.es

 

RESUMEN

En este trabajo nos centramos en la fase de selección de salvaguardas dentro del proceso de análisis y gestión del riesgo en sistemas de la información (SI) bajo un enfoque borroso. Para reducir el riesgo asociado a posibles amenazas en SI se pueden implementar salvaguardas preventivas, paliativas o salvaguardas que disminuyan la probabilidad de transmisión de fallos a través de la red de activos asociada al SI. Sin embargo, las salvaguardas tienen asociadas costes por lo que se debe realizar un proceso de selección de las mismas. En este trabajo describimos problemas de optimización asociados a distintas perspectivas en la selección de salvaguardas y proponemos técnicas de solución basadas en programación dinámica y el uso de metaheurísticas.

Palabras-clave: Análisis y gestión del riesgo; sistemas de información; selección de salvaguardas; lógica borrosa; optimización.

 

ABSTRACT

In this paper we focus on the safeguard selection within the risk analysis and management in information systems (IS) under a fuzzy perspective. Preventive safeguards can be implemented to reduce the risk associated with potential threats in IS, whereas palliative safeguards reduce the probability of failure transmission through the assets network. However, safeguards have associated costs and a selection process has then to be carried out. We describe optimization problems associated with different perspectives on the selection of safeguards and propose solution techniques based on dynamic programming and the use of metaheuristics.

Keywords: Risk analysis and management, information systems, safeguard selection, fuzzy logic, optimization.

 

1. Introducción

Existen numerosas metodologías para el análisis y gestión del riesgo en sistemas de la información (SI) ajustadas a los estándares ISO, específicamente a la familia de estándares ISO 27000 (ISO/IEC, 2011). Algunos ejemplos de dichas metodologías son MAGERIT (López Crespo, Amutio-Gómez, Candau & Mañas, 2006), del Ministerio de Administraciones Públicas (España); CRAMM (CCTA, 2003), de la Central Computing and Telecommunications Agency (Reino Unido); o NIST SP 800-30 (Stoneburner & Gougen, 2002), del National Institute of Standard and Technology (E.E.U.U.)

Sin embargo, las metodologías propuestas por las normas internacionales obvian la dificultad de asignar acertadamente las dependencias entre activos, así como el valor de los activos terminales o el impacto que provocaría sobre todo el sistema la materialización de una amenaza sobre un activo. Estas metodologías tampoco consideran la incertidumbre sobre estas valoraciones.

En (Vicente, Jiménez & Mateos, 2013; Vicente, Mateos & Jiménez, 2013a; Vicente, Mateos & Jiménez-Martín, 2014b) se propone el uso de la lógica borrosa (Zadeh, 1965) como solución a tales deficiencias. Se define una escala de términos lingüísticos, cada uno de los cuales tiene asociado un número borroso trapezoidal (Zadeh, 1975), véase la Figura 1. Los números borrosos trapezoidales asociados a los términos lingüísticos de esta escala son Muy bajo (VL): (0,0,0, 0.25), Bajo (L): (0,0.05,0.15,0.25), Medio-bajo (M-L): (0.15,0.25,0.35,0.45), Medio (M): (0.35, 0.45,0.55,0.65), Medio-alto (M-H): (0.55,0.65,0.75,0.85), Alto (H): (0.75,0.85, 0.95,1) y Muy alto (VH): (0.95,1,1,1).

 

 

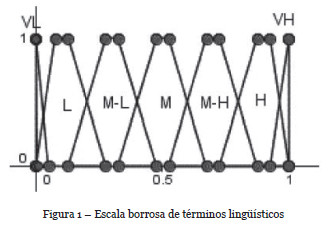
A continuación, se utiliza esta escala para incorporar la imprecisión a la hora de valorar los distintos elementos que forman parte del proceso de análisis y gestión del riesgo en los SI (Ramos, Rodrigues & Perna, 2008; Porta, Parapar, García, Fernández, Touriño, Ónega, Díaz, Miranda & Crecente, 2012), como la valoración de los activos terminales, la dependencia entre éstos, degradaciones y frecuencias asociados a las amenazas, o los efectos de las salvaguardas.

Todos los cálculos se realizan, por tanto, usando los valores borrosos trapezoidales asociados a los términos lingüísticos seleccionados, por lo que se hace necesaria la utilización de una aritmética adecuada, como la propuesta en (Xu, Shang, Qian & Shu, 2010). Denotaremos por 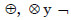, las operaciones suma, producto y resta entre números borrosos trapezoidales, respectivamente.

En la próxima sección hacemos un breve repaso de las etapas de las que consta el proceso de análisis y gestión del riesgo en SI. En la Sección 3 nos centramos en la selección de salvaguardas para la reducción del riesgo, presentando dos perspectivas distintas del problema, las técnicas de solución identificadas y ejemplos ilustrativos. Finalmente, en la Sección 4 presentamos las conclusiones del trabajo.

 

2.Análisis y gestión del riesgo en SI

El valor total de los activos de una organización se concentra generalmente en unos pocos elementos (activos terminales) que suelen ser de tipo “datos” o “servicios”. El valor de estos activos se transmite al resto de activos (de soporte) a través de las relaciones de dependencia establecidas (que dan lugar a un grafo dirigido), de modo que los activos de soporte no tienen valor propio, sino que lo acumulan de los activos terminales.

La dependencia entre activos no tiene por qué ser directa, sino que puede ser transitiva a lo largo del grafo. Es decir, la transmisión de un fallo entre dos activos puede pasar por activos intermedios. Denotaremos por 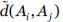el grado de dependencia directo entre dos activos A_i y A_j, mientras que el grado de dependencia de A_i sobre A_k a través de activos intermedios lo denotamos por  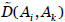pudiendo ser calculados mediante el método recursivo propuesto en (Vicente et al., 2013a; Vicente et al., 2014b).

Los activos terminales se pueden valorar en función de tres componentes: confidencialidad, daño que causaría que lo conociera quien no debe; integridad, perjuicio que causaría que estuviera dañado o corrupto; y autenticidad, perjuicio que causaría no saber exactamente quién hace o ha hecho cada cosa.

Si denotamos el valor propio en los activos terminales por 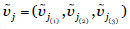, donde 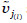será un término lingüístico borroso asignado por un experto para el activo A_j, y por T el conjunto de activos terminales, el valor acumulado del activo A_j respecto de los activos terminales es:

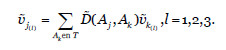
Una amenaza es un evento que puede producir daños materiales o pérdidas inmateriales en los activos de la organización. Para valorar las amenazas debemos tener en cuenta la degradación, perjuicio que la amenaza puede provocar sobre el activo en sus distintas componentes; y su frecuencia, es decir, el número de materializaciones por unidad de tiempo.

Una vez determinadas estas dos medidas se calculan los indicadores de impacto y riesgo. Si consideramos una amenaza sobre el activo A_j cuya degradación en cada componente viene dada por el vector 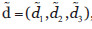 cuando la amenaza se materializa, el impacto de la misma en cada componente del activo será 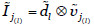, l= 1,2,3. Para calcular el riesgo sobre este activo podemos utilizar la expresión 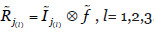, l= 1,2,3.

Una vez calculado el impacto provocado por una amenaza materializada sobre un activo del sistema, podemos calcular el impacto transmitido a los activos que dependen del activo atacado. Si A_j es el activo sobre el que se ha materializado la amenaza y el grado de dependencia de A_j  con respecto a A_k es 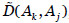 entonces la amenaza sobre el activo A_j provoca un impacto sobre A_k de  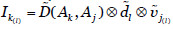y el riesgo sobre el activo será 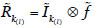, l= 1,2,3.

 

3.Selección de salvaguardas

Las salvaguardas consisten en medidas para tratar las posibles amenazas del sistema y reducir el riesgo total del mismo. Pueden ser procedimientos, como la documentación y gestión de incidentes, políticas de personal, soluciones técnicas; o medidas de seguridad física de las instalaciones.

Las salvaguardas pueden ser preventivas, si reducen la frecuencia de las amenazas, o paliativas, si reducen la degradación causada por las amenazas en los activos. Un caso especial de salvaguarda preventiva es aquélla que reduce la probabilidad de transmisión de fallos en la red de activos, disminuyendo la dependencia entre los activos terminales y los de soporte. Si el efecto de una salvaguarda es 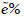, entonces el parámetro correspondiente se reduce en la proporción .

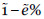Denotaremos los conjuntos de salvaguardas disponibles de la siguiente forma:

• S:{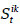, i,k=1,…,n, t=1,…,m_ik}. Salvaguardas que reducen la probabilidad de transmisión de fallos, siendo  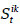la salvaguarda t-ésima que reduce la transmisión de fallos entre los activos A_i y A_k. Su efecto sobre d(A_i,A_k) lo denotamos por .
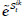• S^(pr):{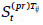, i=1,…,n, j=1,…,n_i, t=1,…, 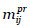}. Salvaguardas preventivas, siendo  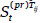la t-ésima salvaguarda preventiva para la amenaza j-ésima sobre el activo A_i. Su efecto sobre la frecuencia de la amenaza T_ij es .
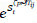• S^(pa):{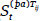, i=1,…,n, j=1,…,n_i, t=1,…, 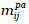}. Salvaguardas paliativas, siendo  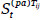la t-ésima salvaguarda paliativa para la amenaza j-ésima sobre el activo A_i. Su efecto sobre la componente l-ésima de la degradación causada por la amenaza T_ij es 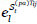, l= 1,2,3.
• Podemos seleccionar distintos paquetes de salvaguardas para reducir el riesgo, que representaremos por los vectores binarios x_ik=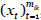, x^pr_ij= 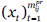y x^pa_ij = 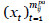respectivamente, siendo x_t=1 si la salvaguarda t-ésima es seleccionada.
• Dentro del proceso de selección de salvaguardas vamos a mostrar dos perspectivas distintas del problema, que estudiaremos en detalle en las dos próximas secciones.

3.1. Selección de salvaguardas que restringen las probabilidades de transmisión de fallos minimizando el coste.

En primer lugar, supongamos que solamente disponemos de salvaguardas que reducen las probabilidades de transmisión de fallos (o grados de dependencia) entre los activos del SI, S. El problema consistirá en seleccionar aquellas salvaguardas que aseguran que no se sobrepasa un umbral en dichas probabilidades entre los activos de soporte y terminales minimizando el coste asociado. El problema de optimización asociado es:

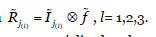
donde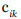 son los vectores de costes asociados a las salvaguardas, u y v en el primer conjunto de restricciones se refieren a activos de soporte y terminales, respectivamente;  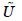es el umbral marcado por los expertos para las probabilidad de transmisión de fallos; y  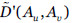se calcula reemplazando los valores de dependencia directa  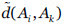por los valores obtenidos teniendo en cuenta las salvaguardas seleccionadas 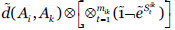, donde A_i y A_k son dos activos consecutivos conectados por un arco en algún camino entre A_u y A_v.

Las restricciones 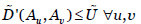 se pueden sustituir por 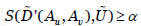, dado un umbral 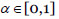, siendo S una función de similitud de números borrosos trapezoidales normalizados, como las propuestas en (Chen, 1996; Vicente, Mateos & Jiménez, 2013b).

Teniendo en cuenta que las dependencias indirectas se pueden calcular mediante el algoritmo recursivo descrito en (Vicente et al., 2013a; Vicente et al., 2014b) a partir de las dependencias de los activos más cercanos, el problema de optimización anterior puede resolverse por etapas, al cumplir el principio de optimalidad requerido en programación dinámica, de la siguiente forma (Vicente et al., 2014b): Sea L₀ el conjunto de nodos terminales.

• Consideramos L₁, conjunto que incluye solo a los activos cuyos hijos pertenecen a L₀. Identificamos las salvaguardas que minimizan los costes manteniendo los grados de dependencia sobre L₀ en un nivel aceptable.
• Consideramos L₂, activos cuyos hijos pertenecen a L₀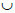L₁. De nuevo, identificamos las salvaguardas que minimizan los costes manteniendo los grados de dependencia sobre L₀ en un nivel aceptable. Nótese que los grados de dependencia indirecta entre los hijos de L₂ y los activos terminales se han calculado ya en la etapa anterior, por lo que simplemente necesitamos identificar los grados de dependencia directa sobre los activos en L₀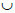L₁.
• …
• Consideramos L_i, activos cuyos hijos pertenecen a L₀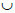L₁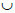...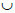L_i-1. De nuevo, identificamos las salvaguardas que minimizan los costes manteniendo los grados de dependencia sobre L₀ en un nivel aceptable. Una vez más, solo tendremos que identificar las dependencias directas sobre los activos en L₀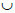...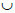L_i-1.

Debido al carácter combinatorio de los problemas de optimización identificados en cada una de las etapas de la programación dinámica, se ha decidido utilizar una metaheurística para su resolución, en concreto el enfriamiento simulado (Kirkpatrick, Gelatt & Vecchi, 1983).

El enfriamiento simulado es una metaheurística trayectorial que considera una solución en cada una de las etapas del proceso de búsqueda de la solución óptima. La idea básica es la siguiente: Partiendo de una solución inicial factible, en cada iteración se genera de forma aleatoria una solución del entorno de la actual. Si la nueva solución es mejor que la actual, entonces el algoritmo se mueve a dicha solución; en caso contrario, existe una cierta probabilidad de que nos movamos a esa solución peor.

La aceptación de movimientos hacia soluciones peores hace la búsqueda del óptimo más dispersa y evita que nos quedemos atrapados en un óptimo local.

La búsqueda se inicia de una forma muy diversificada, en la que prácticamente cualquier movimiento es aceptado. Según avanza, la probabilidad de movernos hacia soluciones peores disminuye haciendo que al final del proceso de búsqueda solo se permitan movimientos hacia soluciones mejores.

Para ilustrar el método de solución propuesto, consideremos el SI y valores de dependencia directa entre activos mostrados en la Figura 2, siendo A₆ el único activo terminal.

 

 

A continuación, se calculan las dependencias indirectas entre los activos de soporte y el terminal (A₆) (Vicente et al., 2013).

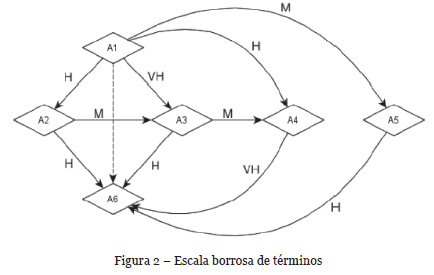
Consideremos una amenaza sobre el activo A₁ con frecuencia 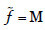y degradación 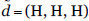. Entonces, el riesgo sobre el activo A₁ es 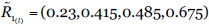, l= 1,2,3.

Tomamos como umbral 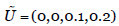, por debajo del cual el grado de dependencia o probabilidad de transmisión de fallos entre activos será aceptable, siendo  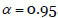Supongamos que el conjunto de salvaguardas disponibles es el que se muestra en la Tabla 1.

 

 

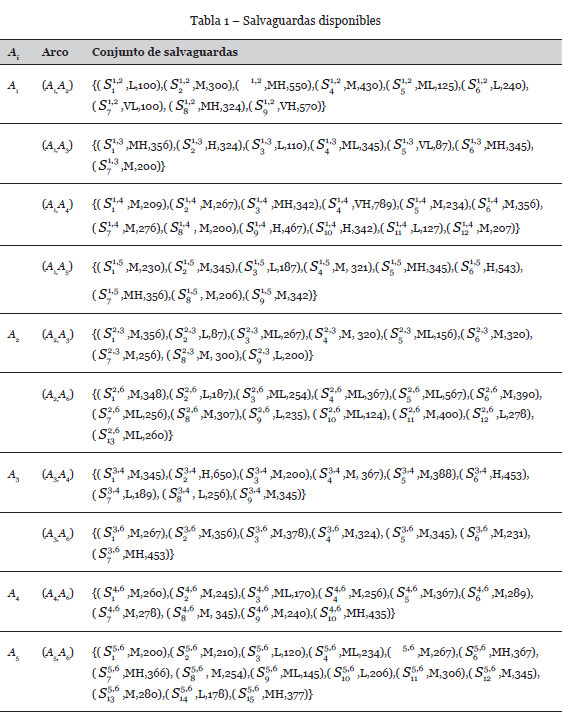
Aplicamos la técnica de solución propuesta para la selección de salvaguardas. Inicialmente L₀={A₆}.

• L₁={A₄,A₅}. Debemos ajustar los grados de dependencia,

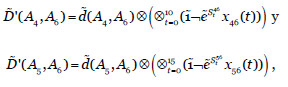
tales que 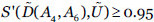 y 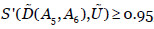en función de las salvaguardas que se seleccionen.

Como L₁ contiene dos elementos, se deben resolver dos problemas de optimización.

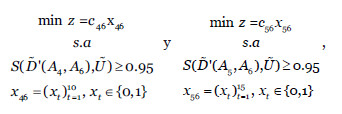
que utilizando enfriamiento simulado nos proporcionan la selección óptima de salvaguardas 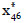=(0,1,1,1,0,0,0,0,1,0) y 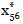=(1,0,0,0,0,0,1,0,1,0, 0,0,0,0,0).

• L₂={A₃}. Ahora, ajustamos el grado de dependencia

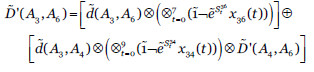
tal que 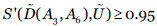, en función de las salvaguardas que se seleccionen. Nótese que el valor  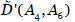ya se obtuvo al resolver el problema de optimización de la etapa anterior, (0.016,0.072,0.104,0.269).

El problema de optimización a resolver es:

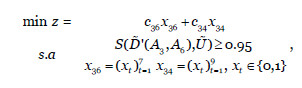
cuya solución óptima es 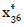=(1,0,0,1,0,1,1) y 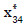=0.

• L₃={A₂}. Ajustamos el grado de dependencia

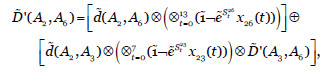
siendo 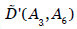 =(0.008,0.059,0.096,0.301), obtenido de la etapa anterior. El problema de optimización a resolver es:

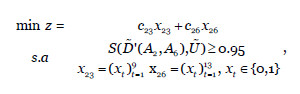
que proporciona la selección óptima 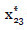=(0,0,0,0,0,0,1,0,0) y 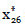=(1,0,0, 0,1,0,1,0,0,1,0,0,0).

• Finalmente, L₄={A₁}. Ajustamos

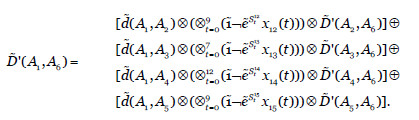
Ahora, resolvemos el problema de optimización:

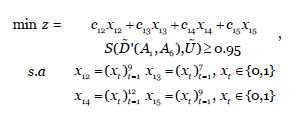
que nos proporciona la selección óptima de salvaguardas 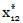=(1,0,0,0,0, 0,0,0,0), 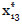=(0,1,0,0,0,0,0), 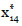= (0,0,0,0,0,0,0,0,0,1,0,0) y 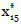=0

Tras la implementación de las salvaguardas seleccionadas, el riesgo sobre el activo A₁ es 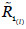(0.001,0.018,0.039,0.22), l=1,2,3.

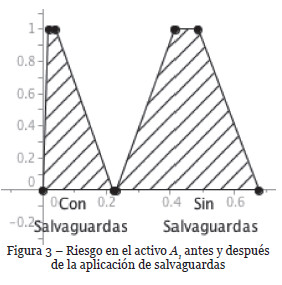
En la Figura 3 se puede comparar el riesgo sobre el activo A₁ antes y después de la aplicación de las salvaguardas.

 

 

3.2. Selección de salvaguardas que minimizan el riesgo del sistema para un presupuesto disponible.

Consideremos ahora de forma adicional los conjuntos de salvaguardas preventivas, S^(pr), y salvaguardas paliativas, S^(pa), y deseamos seleccionar aquellas salvaguardas que minimizan el riesgo del sistema dado un presupuesto.

El problema de optimización a resolver es, por tanto, el siguiente (Vicente, Mateos, & Jiménez-Martín, 2014a):

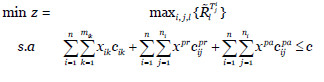
donde c_ik, 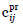 y 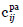 son los vectores de costes de las salvaguardas y c es el presupuesto disponible.

Es importante destacar que las amenazas deben ser consideradas de forma secuencial para computar el riesgo en el SI en lugar de considerar que todas ellas se producen simultáneamente. Como consecuencia, tenemos un problema de optimización borroso multiobjetivo cuyas funciones objetivo representan nuevos riesgos (reducidos) como resultado de la aplicación de las salvaguardas. Por lo tanto, dichos riesgos no deben ser sumados y, por ello, hemos decidido minimizar el máximo de los mismos.

La función objetivo necesita de un orden total en su argumento del cuál carecen los números borrosos trapezoidales. Se han propuesto más de 30 métodos para ordenar números borrosos trapezoidales (Bortolan & Degani, 1985; Wang & Kerre, 2001a-b; Brunelli & Mezei, 2013). 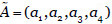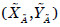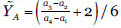En este trabajo usamos el índice de Murakami (Murakami, Maeda & Imamura, 1983), que calcula el centroide de los números borrosos comparados: Si , entonces su centroide es , con    y.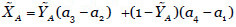

El índice compara primero las abscisas de los centroides de forma que los números borrosos con mejor abscisa son ordenados mejor. Si las abscisas son iguales, entonces aquél con mayor ordenada es el mejor.

Como ejemplo ilustrativo, consideremos ahora el SI y valores de dependencia directa entre activos mostrados en la Figura 4, siendo A₅ el único activo terminal. 

 

 

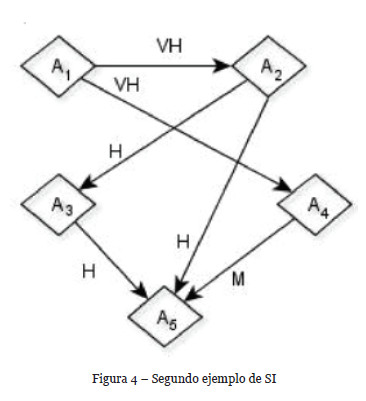
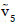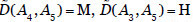
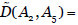
El valor monetario (en cientos de unidades) del activo terminal es ((10,15,20,25),(18,20,23,30),(12,15,26,30)). Las dependencias indirectas entre los activos no terminales y el terminal (A₅) son  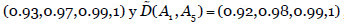 , véase (Vicente et al., 2014a).

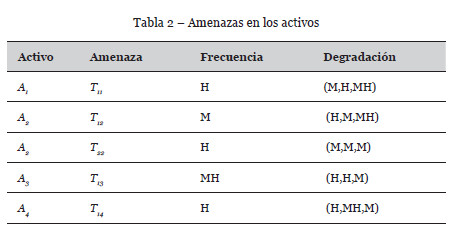
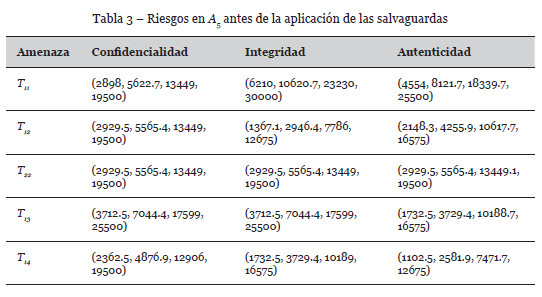
Si consideramos las 5 amenazas mostradas en la Tabla 2, los riesgos inducidos por cada amenaza individual se muestran en la Tabla 3.

 

 

 

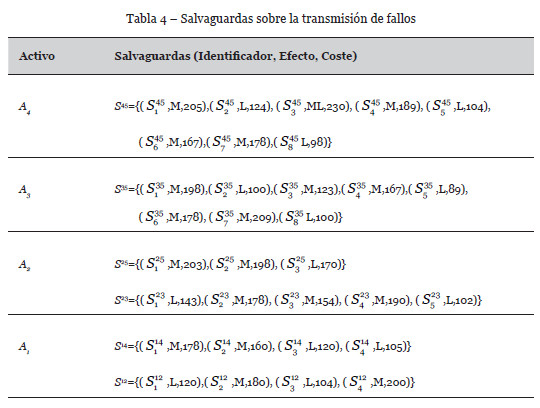
Si ahora consideramos las salvaguardas mostradas en las Tablas 4, 5 y 6, y disponemos de un presupuesto de 5000 unidades, el problema de optimización a resolver es:

 

 

 

 

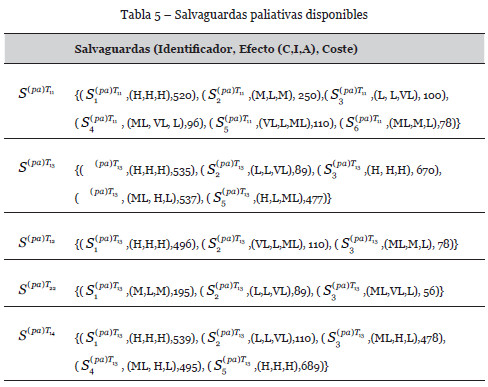
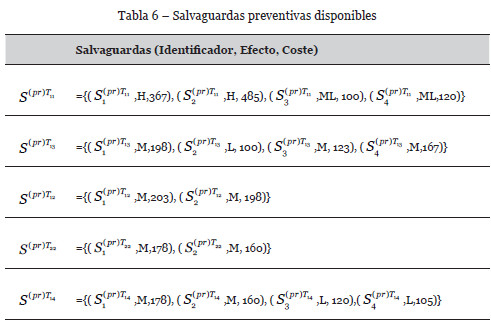
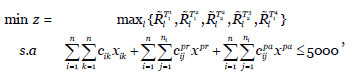
donde, por ejemplo, el primer y último término de la función objetivo son:

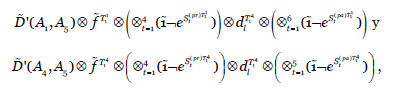
y 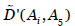se obtiene de 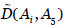multiplicando el valor inicial de cada arco por la reducción causada por el efecto de las salvaguardas de transmisión de fallos en dicho arco.

En la Tabla 7 se muestra la solución obtenida utilizando el enfriamiento simulado, con un coste asociado de 4850 unidades, mientras que la Tabla 8 muestra los nuevos valores de riesgo en el activo terminal A₅ una vez que las salvaguardas han sido implementadas.

 

 

 

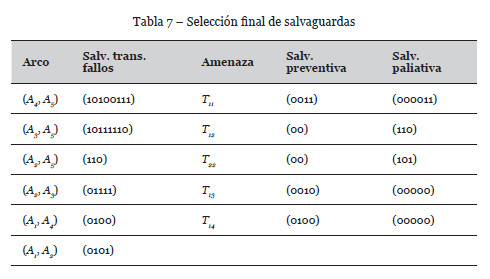
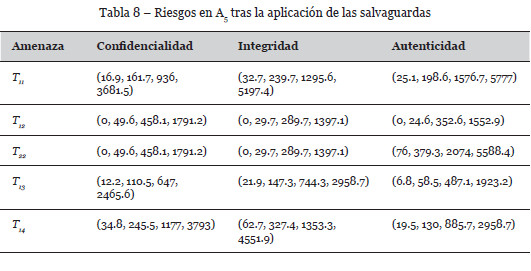
Si comparamos los riesgos mostrados en las Tablas 3 y 8, antes y después de la implementación de salvaguardas, podemos apreciar que la reducción del riesgo es significativa.

 

4. Conclusiones

En este trabajo se han analizado los problemas de selección de salvaguardas en la gestión del riesgo en sistemas de la información (SI) desde dos perspectivas. En la primera, únicamente hemos considerado salvaguardas que disminuyen la probabilidad de transmisión de fallos en la red de activos y el problema de optimización planteado minimiza los costes asociados a las salvaguardas seleccionadas que mantienen dichas probabilidades de transmisión de fallos entre activos de soporte y terminales en unos niveles aceptables.

En el segundo enfoque, se disponen tanto de salvaguardas preventivas y paliativas, como de salvaguardas que disminuyen la probabilidad de transmisión de fallos y se seleccionan las salvaguardas que minimicen el riesgo del sistema sin sobrepasar un presupuesto disponible.

Ambos problemas de optimización se han resuelto de una manera eficiente. En el primer caso, mediante el uso de programación dinámica y enfriamiento simulado para resolver los problemas asociados a cada una de sus fases; y en el segundo, mediante el uso directamente de la metaheurística.

 

Referencias bibliográficas

Bortolan, G., & Degani, R. (1985). A review of some methods for ranking subsets. Fuzzy Sets and Systems, 15, 1-19. doi: http://dx.doi.org/10.1016/0165-0114(85)90012-0        [ Links ]

Brunelli, M., & Mezei, J. (2013). How different are ranking methods for fuzzy numbers? A numerical study. International Journal of Approximate Reasoning, 54, 627-639. doi: http://dx.doi.org/10.1016/j.ijar.2013.01.009        [ Links ]

Central Computing and Telecommunications Agency (2003). Risk analysis and management method (CRAMM), V5.0. London.

Chen, S. M. (1996). New Methods for subjective mental workload assessment and fuzzy risk analysis. Cybernetics Systems, 27, 449-472. doi: http://dx.doi.org/10.1080/019697296126417        [ Links ]

International Organization for Standardization (2011). ISO/IEC 27005:2011 Information technology – security techniques – information security risk management. Geneva.

Kirkpatrick, S., Gelatt, D. C., & Vecchi, C. D. (1983). Optimization by simulated annealing. Science, 220, 671-680. doi: http://dx.doi.org/10.1126/science.220.4598.671        [ Links ]

López Crespo, F., Amutio-Gómez, M. A., Candau, J., & Mañas, J. A. (2006). Methodology for information systems risk. Analysis and management (MAGERIT version 2). Books I, II and III, Madrid, Spain: Ministerio de Administraciones Públicas.         [ Links ]

Murakami, S., Maeda, S., & Imamura, S. (1983). Fuzzy decision analysis on the development of centralized regional energy control system. IFAC Symposium on Fuzzy Information Knowledge Representation and Decision Analysis, 363-368.         [ Links ]

Porta, J., Parapar, J., García, P., Fernández, G., Touriño, J., Ónega, F., Díaz, P., Miranda, D., & Crecente, R. (2012). Sistema de información del banco de tierras de Galicia, Revista Ibérica de Sistemas y Tecnologías de la Información, 9, 27-41. doi: http://dx.doi.org/10.4304/risti.9.27-41        [ Links ]

Ramos, C., Rodrigues, P. M. M., & Perna, F. (2008). Sistemas de Informaçao para apoio ao turismo, o caso dos dynamic packaking, Revista Ibérica de Sistemas y Tecnologías de la Información, 2, 25-35.         [ Links ]

Stoneburner, G., & Gougen, A. (2002). NIST 800-30 risk management. Guide for information technology systems, Gaithersburg, USA: National Institute of Standard and Technology.         [ Links ]

Vicente, E., Jiménez, A., & Mateos, A. (2013). A Fuzzy Approach to Risk Analysis in Information Systems. Proceedings of the 2nd International Conference on Operations Research and Enterprise Systems, 130-133.         [ Links ]

Vicente, E., Mateos, A., & Jiménez, A. (2013a). A Fuzzy Extension of MAGERIT Methodology for Risk Analysis in Information Systems. Proceedings of the IADIS Information Systems Conference, 39-46.         [ Links ]

Vicente, E., Mateos, A., & Jiménez, A. (2013b). A New Similarity Function for Generalized Trapezoidal Fuzzy Numbers. In L. Rutkowski, M. Korykowski, R. Scherer, R. Tadeusiewizc, L. Zadeh & J. Zurada (Eds.), Lecture Notes on Computer Science: Vol. 7894. (pp. 400-411). Berlin: Germany, Springer. doi: http://dx.doi.org/10.1007/978-3-642-38658-9_36        [ Links ]

Vicente, E., Mateos, A., & Jiménez-Martín, A. (2014a). Selection of Safeguards for Fuzzified Risk Management in Information Systems. In A. Rocha, A. M. Correira, F. B Tan & K. A. Stroetmann (Eds.), Advances in Intelligent Systems and Compu-ting: Vol. 275. New Perspectives in Information Systems and Technologies (pp. 267-276). Berlin: Germany, Springer. doi: http://dx.doi.org/10.1007/978-3-319-05951-8_26        [ Links ]

Vicente, E., Mateos, A., & Jiménez-Martín, A. (2014b). Risk analysis in information systems: a fuzzification of the MAGERIT methodology. Knowledge-Based Systems, 66, 1-12. doi: http://dx.doi.org/10.1016/j.knosys.2014.02.018        [ Links ]

Wang, X., & Kerre, E. E. (2001a). Reasonable properties for the ordering of fuzzy quantities (I). Fuzzy Sets and Systems, 118, 375-385. doi: http://dx.doi.org/10.1016/S0165-0114(99)00062-7        [ Links ]

Wang, X., & Kerre, E. E. (2001b). Reasonable properties for the ordering of fuzzy quantities (II). Fuzzy Sets and Systems, 118, 387-405. doi: http://dx.doi.org/10.1016/S0165-0114(99)00063-9        [ Links ]

Xu, Z., Shang, S., Qian, W., & Shu, W. (2010). A Method for fuzzy risk analysis based on the new similarity of trapezoidal fuzzy numbers. Expert Systems and Applications, 37, 1920-1927. doi: http://dx.doi.org/10.1016/j.eswa.2009.07.015        [ Links ]

Zadeh, L. A. (1965). Fuzzy sets. Information and Control, 8, 338-353. doi: http://dx.doi.org/10.1016/S0019-9958(65)90241-X        [ Links ]

Zadeh, L. A. (1975). The Concept of a linguistic variable and its application to approximate reasoning. Parts 1, 2 and 3. Information Sciences, 8, 199-249. doi: http://dx.doi.org/10.1016/0020-0255(75)90036-5        [ Links ]

 

Recebido / Recibido: 15/1/2015

Aceitação /Aceptación: 1/6/2015

 

Agradecimientos

El trabajo ha sido financiado por el proyecto del Ministerio de Ciencia (España) MTM2011-28983-CO-03 y el Ministerio de Economía y Competitividad MTM2014-56949-C3-2-R.